用于CPM的LT碼設計*

袁磊

（蘭州大學 信息科學與工程學院，甘肅 蘭州 730000）

連續相位調制 CPM（Continuous Phase Modulation）是一種恒包絡調制信號，具有較高的頻譜利用率和功率利用率，其非常適用于使用非線性功率放大器的系統中。CPM可以分解為連續相位編碼和無記憶調制器的組合[1]。由于CPM可以看成是串行級聯系統中的內碼，因而提出了 Turbo碼[2]和IRA碼［3］作為外碼，與 CPM 構成串行級聯編碼調制系統。LT碼是第一類實用噴泉碼[4]，不同于Turbo碼等固定率碼，LT碼是一種無比率編碼，其非常適合應用在時變信道和組播信道中。LT碼最初是為刪除信道設計的[5]，現已擴展到加性高斯白噪聲AWGN（Additive White Gaussian Noise）信道[6-7]中，且以往研究都是基于LT碼和二進制相移鍵控相結合。本文將研究LT碼與CPM構成串行級聯編碼系統的問題，運用迭代原理設計了基于軟輸入軟輸出的迭代檢測譯碼算法，采用高斯近似的密度進化方法[8]優化設計了LT碼的度分布函數，最后通過計算機仿真進行了驗證。

1 LT-CPM系統模型

CPM信號的數學表達式為：

其中，E為符號能量，T為符號周期，f0為中心載波頻率，φ0為載波初始相位。φ（t，β）負責承載信息，其表達式為：

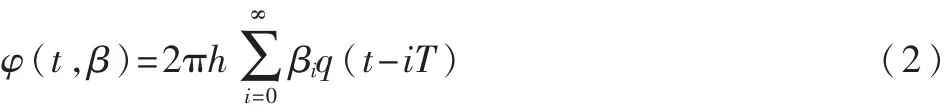
其中，h 為調制指數，{βi}為 發 送符號 序列，βi∈{±1，…，±（M-1）}，M 為調制進制數。 q（t）為 CPM 信號的相位響應，其表達式為：

其中，g（t）為基帶調頻脈沖函數。

LT碼的編碼比特產生過程為：首先，根據度分布函數 Ω（x）隨機選取一個度值d；其次，在信息比特中隨機選取d個信息比特；最后，d個信息比特進行模二加運算產生編碼比特。LT碼采用隨機編碼思想，可以產生任意多的編碼比特。

CPM結合外部的LT碼構成了串行級聯的LT-CPM通信系統，其系統框圖如圖1所示。不同于Turbo-CPM系統，由于LT碼具有隨機編碼特性，當外碼是LT碼時，串行級聯系統可省略使用交織器。假定長度為k的信息字s采用度分布函數為 Ω（x）的 LT碼編碼器產生n個編碼比特c。定義γ=n/k為LT碼的譯碼開銷。n個編碼比特經過符號映射輸入到M進制CPM。CPM中的無記憶調制器選擇一個合適的波形發送到AWGN信道中。本文采用了參考文獻[2]中兼顧了功率效率和帶寬效率的CPM參數，調制進制數為8，脈沖波形為升余弦脈沖，關聯長度為2個符號周期。在接收到信號序列r后，系統運行解調與譯碼程序，其過程是通過CPM解調的BCJR算法[9]和LT碼譯碼的置信傳播BP（Belief Propagation）譯碼迭代完成的。

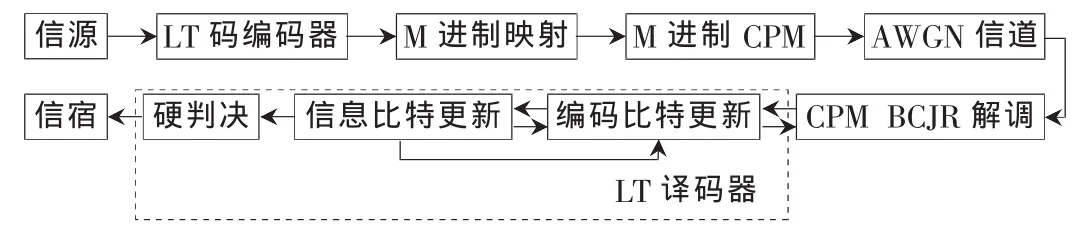
圖1 LT-CPM系統模型

在第1次迭代解調譯碼時，BCJR譯碼算法[10]利用信道接收序列r和LT碼譯碼器提供的外部對數似然比LLR（Log-Likelihood）L（c）信息（初始時，L（c）＝0）獲得第i編碼比特的LLR值消息

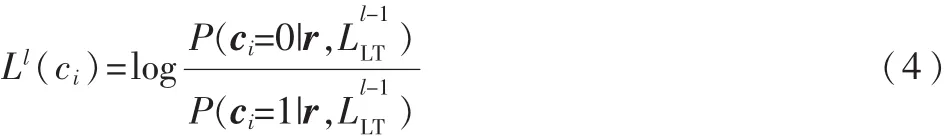
則CPM解調器提供給LT碼譯碼器的外部LLR值消息為：

LT碼BP譯碼處理過程為：

對于閱讀推廣而言，產品形象就是服務形象，它反映了品牌形象與服務的牢固聯系，是品牌形象的核心構成要素。在這個要素中，品質是關鍵，創新性的活動設計和讀者認可的高價值感將促進品牌形象的成功塑造。個性形象是指品牌擁有的人格特性，它能使品牌形象更加生動和有趣。比如針對青少年閱讀推廣的品牌個性形象可以賦予其朝氣的、富于想象的、精力充沛的特征等。

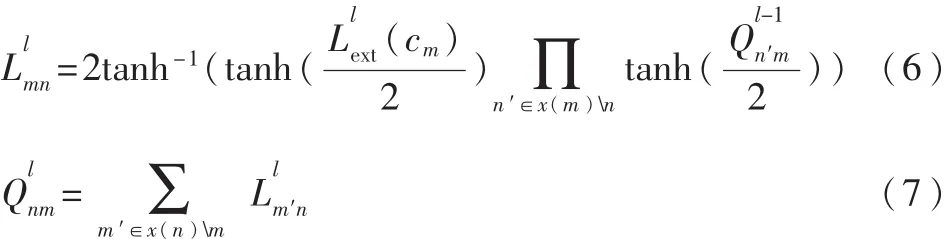
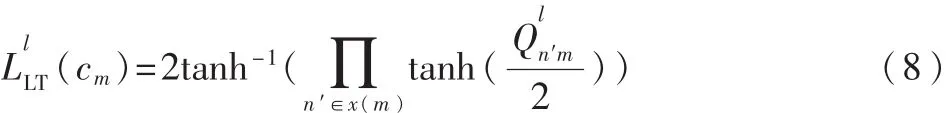
在CPM解調器和LT碼譯碼器級聯運行q次后，第i個信息比特的譯碼判決LLR值為

2 碼優化設計

本文采用高斯近似的密度進化方法優化設計了LT-CPM系統中LT碼的度分布函數。CPM可以分解為碼率為1的卷積碼和無記憶調制的組合，在給定的信道噪聲方差下，通過蒙特卡羅仿真的方法獲得CPM在BCJR解調算法下的輸入輸出關系曲線。在漸進分析中，假定傳遞的LLR信息服從對稱高斯分布，即方差為均值的 2倍。 為了對 LT碼進行分析，用 δ（x）和 ω（x）分別表示信息比特和編碼比特的邊度分布函數。在漸進情況下，信息比特的邊度分布函數是泊松分布函數，即

其中，θ表示信息比特度的平均值。

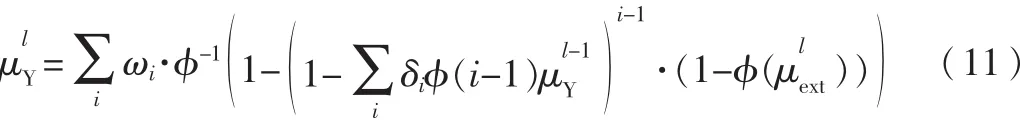
為方便計算，可簡化為

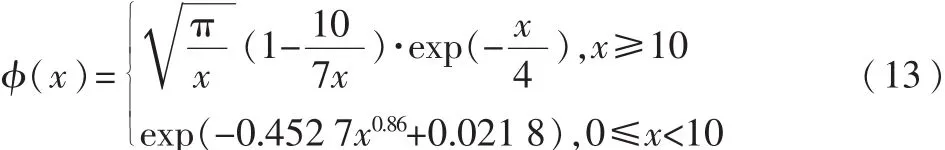
其中，thah（·）和 exp（·）分別表示雙曲正切函數和指數函數。

使用漸進分析公式能夠優化設計LT碼的度分布函數Ω（x）。在固定的信道方差 σ2和信息比特度平均值下，設定 μ的最大值為 μm最大編碼比特度為 D。LT碼在BP譯碼下最優度分布函數設計方法是：

約束條件為：

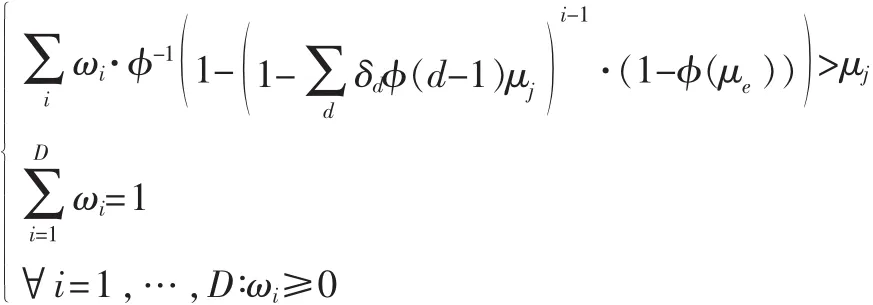
其中，μj（j=1，…，N）是把區間[0，μm]N 等分的各點值，μe則可通過把μj-1代入CPM在BCJR算法下的輸入輸出關系曲線獲得。本文給出一個具體例子，令σ2=1、θ=20、μm=30和N＝2 000，則優化后的輸出比特節點度分布函數為：

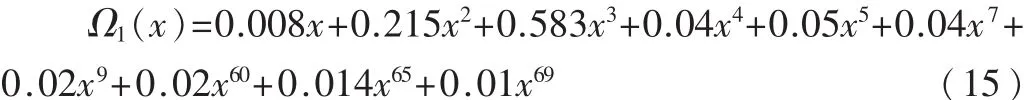
3 仿真分析

為了驗證設計的有效性，本文進行了計算機仿真實驗。在仿真實驗中，AWGN信道方差為1，信息字長度取為10 000，迭代譯碼次數為80次。圖2為不同譯碼開銷下的誤碼率仿真曲線。度分布函數分別采用了本文優化的度分布函數式（15）和參考度分布函數[7]：

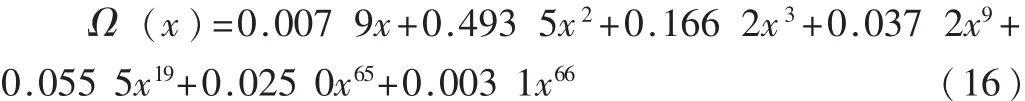
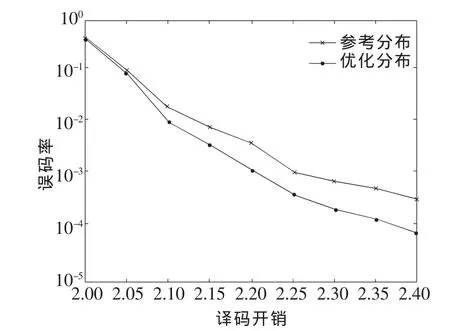
圖2 不同譯碼開銷下的誤碼率仿真結果

由圖2可以看出，采用本文優化的度分布函數能夠獲得更好的誤碼率性能。

CPM是一種高效的調制方式，本文研究了LT碼與CPM構成的串行級聯編碼系統，給出了迭代譯碼算法，并運用高斯近似的密度進化方法優化了LT碼的度分布函數，最后進行了計算機仿真驗證，為LT碼在無線通信系統中的應用提供了新的依據。

[1]RIMOLDI B E.A decomposition approach to CPM[J].IEEETransactions on Information Theory.1988， 34（2）：260-270.

[2]趙旦峰，薛睿，肖春麗.Turbo-CPM系統在窄帶低信噪比條件下的性 能研究[J].高技術 通 訊，2010，20（7）：685-689.

[3]Xiao Ming，AULIN T.Irregular repeat continuous phase modulation[J].IEEE Communications Letters， 2005， 9（8）：723-725.

[4]LUBY M.LT codes[C].Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science，2002：271-282.

[5]袁磊，安建平，楊靜，等.LT碼的一種 BP/ML混合譯碼算法[J].高技術通訊，2011，21（1）：54-57.

[6] JENKAC H， MAYER T， STOCKHAMMER T.Soft decoding of LT codes for wireless broadcast[C].Proceedings IST Mobile Summit 2005， 2005： 262-264.

[7]ETESAMI O，SHOKROLLAHI A.Raptor codes on binary memoryless symmetric channels[J].IEEE Transactions on Information Theory， 2006， 52（5）： 2033-2051.

[8]CHUNG S Y， RICHARDSON J， URBANKE R L.Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J].IEEE Transactions on Information Theory， 2001， 47（2）： 657-670.

[9]BAHL L， COCKE J， JELINEK F， et al.Optimal decoding of linear codes for minimizing symbol error rate[J].IEEE Transactions on Information Theory， 1974，20（2）：284-287.