在經歷中體驗 在體驗中探索
——《分數的初步認識》的教學設計與反思

■ 萬江南

在經歷中體驗 在體驗中探索
——《分數的初步認識》的教學設計與反思

■ 萬江南

數學課程標準倡導數學教育要從以獲取知識為首要目標轉變為首先關注人的發展。數學課標明確指出：“課程設計要符合數學科學本身的特點、體現數學科學的精神實質；要符合學生的認知規律和心理特征、有利于激發學生的學習興趣；要在呈現作為知識與技能的數學結果的同時，重視學生已有的經驗，讓學生體驗從實際背景中抽象出數學問題、構建數學模型、得到結果、解決問題的過程。”細細研讀課標，我們還發現其中不僅使用了“了解（認識）、理解、掌握、靈活運用”等刻畫知識技能的目標動詞，而且使用了“經歷（感受）、體驗（體會）、探索”等刻畫數學活動水平的過程性目標動詞。這說明，新課改要促進學生的學習方式由“學數學”轉變為“做數學”，讓學生親身經歷數學知識的形成過程，經歷豐富而生動的思維活動過程，經歷實踐和創新的過程，為學生的終身學習和可持續發展打下基礎。因此，我在設計《分數的初步認識》一課時，注重讓學生在“經歷、體驗、探索”的過程中認識分數，理解分數、運用分數。

【教學設計】

師：今天我們要學習一些新知識。老師給同學們準備了一些學具，請你們打開桌上的文件袋，同桌的兩位同學自己動手分一分。（每個文件袋中裝了7張不同形狀的紙，如：4張同樣大的長方形紙片、2張同樣大的正方形紙片、1張圓形紙片；4張同樣大的正方形紙片、2張同樣大的圓形紙片、1張三角形形紙片……）

生1：（學生動手分學具的過程中，產生疑問）老師，我們文件袋中的圓形只有一個，不夠兩個人分！

生2：我們也只有一個三角形！

生3：我們也只有一個平行四邊形！……

師：文件袋中僅有一種圖形的那張紙兩個人就不能分了嗎？

學生們遲疑了，互相之間嘀咕起來。不一會兒，有的學生舉起了桌上的剪刀，興奮地叫道：可以——可以。“一張紙兩個人能不能分？”我趁熱打鐵地又問了一遍。

生：能！

【設計意圖】開課時教師創設的分學具活動，既溝通了整數與分數“平均分”的聯系，又為學生創設了經歷、體驗分數產生的問題情境，可謂“一箭雙雕”。

學生們堅定地回答后，同桌兩人開始分起僅有的一種圖形的那張紙。接下來開始小組交流匯報分的結果。

生1：我們每人分到2張長方形紙、1張正方形紙和半張圓形的紙。

生2：我們每人分到2張圓形紙、1張長方形紙和半張正方形的紙。

……

師：老師給你們準備的學具各不相同，但你們分學具的方法有相同之處嗎？

生1：我們都是把4個的那種圖形每人分2個，2個的那種圖形每人分1個，1個的那種圖形每人分半個。

生2：我們同座兩人分得的學具是同樣多的。

生3：我們都是把這些學具平均分的。

師：同學們真了不起，都能用平均分這種方法來公平、合理地分這些學具。老師很想看看你們是怎樣把1張紙平均分成2份的，哪位同學愿意上來演示？

生1：我們把一張長方形的紙先對折成兩個同樣大的部分再剪開，每人就得到這張長方形紙的一半。

生2：我們把一張三角形的紙先對折成兩個同樣大的小三角形再剪開，每人就得到這張三角形紙的一半。

生3：我們把一張平行四邊形的紙先對折成兩個同樣大……哦，不對，不對……（這位同學沒說完就不好意思地坐下了，原來他發現自己分的圖形一邊大，一邊小）

……

師：原來把1張紙平均分成2份，就是把它分成兩個同樣多的部分。每人得到它的一半，像這樣一半的數該怎樣表示呢？

學生在黑板上用自己的方法表示“一半”，歸納起來主要是三種方式：畫圖，0．5，。師肯定前兩種方式，著重就提問。

師：這個數誰會讀？

生：（部分學生齊答）二分之一。

師：對，把1張紙平均分成2份，每人得到它的一半，也就是它的二分之一，今天我們就要學習像這樣的分數。你能把你剛才分那一張紙的過程用說一句話嗎？

……

生1：媽媽把一塊巧克力平均分給我和妹妹，我就得到了這塊巧克力的。

生2：教室的一扇窗戶由兩塊同樣大的玻璃組成，每塊玻璃就是這扇窗戶的。

……

【設計意圖】波利亞說過：“學習任何知識的最佳途徑是自己去發現，因為這種發現理解最深，也最容易掌握其中的規律、性質、聯系。”當學生產生兩個人分1張紙的需要后，他們自然會運用已有的“平均分”的知識去體驗把一張紙平均分成兩份的過程。正因為有了經歷和體驗，他們才能用自己的語言準確地說出的含義，并舉出生活中能用表示的例子。

（學生活動后，師展示學生作品）

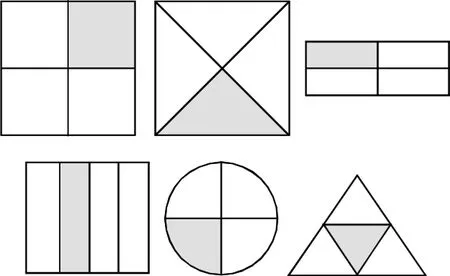
師：這些圖形的形狀，折法各不相同，它們的陰影部分為什么都可以用表示？

生：因為他們都是把那個圖形平均分成了4份，其中的一份就是那個圖形的。

（生答略）

【設計意圖】有效的數學學習活動不能單純地依賴模仿與記憶，讓學生在合理猜測、動手實踐、合作交流的過程中進一步探索的意義，對后續學習是積極而有意義的。

三、想一想，說一說，深化對幾分之一的認識

師：請你想一個分數，用紙折出來并涂上顏色，待會兒在四人小組內給別的同學猜一猜。猜的同學不僅要說出這個分數，還要說說你是怎樣想出來的？

（學生們高興地在四人小組內折紙、猜分數，老師參加學生活動，并選取有代表性的作品展示在黑板上）

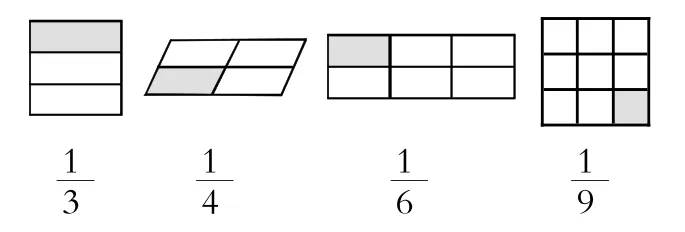
【設計意圖】通過“做中學”“玩中學”讓學生進一步體驗探索數學知識的快樂。拓展題也充分體現了不同的學生在數學上得到不同的發展這一理念。

四、比一比，辯一辯，探索比較幾分之一大小的一般方法

（師隨機從學生折紙作品中拿出由同樣大小的紙折出的不同分數）

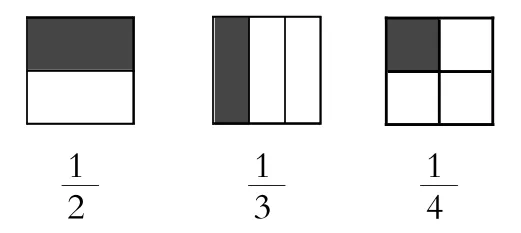
【設計意圖】生踴躍辯論，在爭論中通過對幾分之一的理解來比較幾分之一的大小，既深化了對幾分之一的理解，又探索出了比較幾分之一大小的方法。

五、小結

師：今天你有什么收獲？你還有什么問題？

（生答略）

【教學反思】

這節課的教學，我以建構主義理論為指導，將他們置于一個熟悉的情境中自主地去提出問題，去經歷體驗知識的產生、形成過程，并在此基礎上積極探索，將新知識納入到自己的知識體系中。

1．讓學生在親身經歷中發現問題

建構主義認為課堂應是學生主動構建自己有效數學理解的場所。因此，教師要善于將新知識和學生已有的知識經驗相聯系，改呈現知識為創設適合學生探索的問題情境，從而吸引學生充分參與到數學學習過程中來，自覺調動已有知識經驗和心智技能開展有效而充分的數學活動。開課時，老師就給學生創設了一個“同座兩人分學具”的情境，學生自然就用到了生活中最常用的，也是最公平的方法——“平均分”。接下來，老師預設的問題“有的形狀的紙只有一張，兩人怎么分？”就自然而然地由學生提出來了。

2．讓學生在親身體驗中建構概念

認知心理學家認為：活動是認知的基礎，智慧從動作開始。對于動作形象思維占優勢的小學生來說，聽過了，就忘記了;看過了，就明白了；做過了，就理解了。他們最深刻的體驗莫過于自己雙手實踐過的東西。學生對自己提出的問題往往是最感興趣的，因而他們能興致勃勃地用已有的“平均分”的經驗開始分起了那一張紙。正因為學生在分紙的過程中經歷了分數的產生，體驗了把一張紙平均分成兩份的過程，因而才能用自己的語言準確地說出其含義，才能準確地舉出生活中的例子。

3．讓學生在自主探索中品味成功

在學生真正理解的基礎上，教師讓學生先猜含義再折紙驗證，并從不同的個例中找出相同之處，從而深化學生對幾分之一的認識，最后再放手讓學生在游戲中去折自己想折的分數，猜別人折出的分數……在這個“做數學”的過程中，教師沒有說教，卻讓學生因自身的需要產生了積極的探究欲望。整節課學生都樂在其中，獲得了豐富的情感體驗，較好地完成了本課的三維目標。

總而言之，教師要把數學課堂建設成學生發現、探究、交流數學知識、建構自己數學理解的場所。把“經歷”的機會讓給學生，把“體驗”的過程留給學生，把“探究”的時空交給學生，讓學生在經歷中體驗，在體驗中探索，這不僅可以幫助學生理解和掌握相應的數學知識，體會數學與生活的密切聯系，還有利于培養他們獨特的思維個性和解決問題的能力，更有利于學生體驗成功的喜悅，促進學生全面和諧的發展。

（作者單位：湖北省武昌水果湖二小）

責任編輯王愛民