新型混接式腳手架極限承載力研究＊

周 盛 李 瑞 汪 洋

（武漢理工大學能動學院1） 武漢 430063） （大連理工大學船舶工程學院2） 大連 116024） （大連中遠船塢工程有限公司3） 大連 116113）

0 引 言

本文的研究對象是一種用于LNG 船內艙建造的新型腳手架，其主要特點是桿件先通過焊接形成若干組件，組件之間再通過插銷連接成腳手架，這種混合連接方式使其力學性能不同于傳統(tǒng)腳手架，其中腳手架的極限承載力與穩(wěn)定性一直是人們最關心的問題.徐崇寶等提取雙排腳手架進行了理論分析和試驗研究，得到多層多跨空間框架節(jié)點剛性處理時，不同約束情況下的整體屈曲特征值和屈曲模態(tài)［1］.敖鴻斐對雙排腳手架整體穩(wěn)定極限承載力提出了通用計算方法［2］.Weesner和Jones對4種不同形式的高承重腳手架在足尺寸下的極限承載力進行試驗研究，運用有限元法計算得到了腳手架分支形屈曲和極值點屈曲的分析結果［3］.Godley研究了扣件式鋼管腳手架的二維與三維模型對計算剛度的影響程度，分析節(jié)點半剛性對腳手架動力特性研究的重要性［4］.

以上這些研究成果為不同類型的腳手架失穩(wěn)分析提供了豐富的基礎理論與計算方法.本文通過有限元法計算該混接式腳手架的極限承載力，評估其穩(wěn)定性：首先計算該腳手架的4種主要失穩(wěn)形式以及各種失穩(wěn)形式下的極限承載力；之后分析腳手架極限承載力的主要影響因素，其中包括：立桿縱距、立桿步距、步數(shù)，以及連墻件位置；最后與同尺寸扣件式腳手架比較極限承載力的不同.本文的研究成果將為該類混接式腳手架的使用與維護提供理論依據(jù).

1 腳手架極限承載力理論計算方法

插銷式鋼管腳手架主要是靠框架立桿軸心受壓將豎向荷載傳給基礎.所以，插銷式鋼管腳手架主要受軸向壓力，雖有彎矩作用，但所產生的附加應力不大.因此壓桿的穩(wěn)定很大程度上決定了腳手架的承載力的大小.對于端部有約束（包括鉸接、剛接、半剛接和自由端）的軸心受壓構件可以用下述方法來其確定其極限承載力［5］.

如圖1a）所示，構件上端和下端彈性的抗彎彈簧常數(shù)分別為rB和rA，而上端平移的彈性彈簧常數(shù)為kR.構件的變形和作用于構件兩端的力見圖1b），在圖中以順時針的轉角為正，以右的平移為正，柱端的力矩和水平力以與位移同方向時為正，異向時為負.取圖1c）所示的隔離體，建立力矩和與x 軸相垂直的水平力的平衡方程

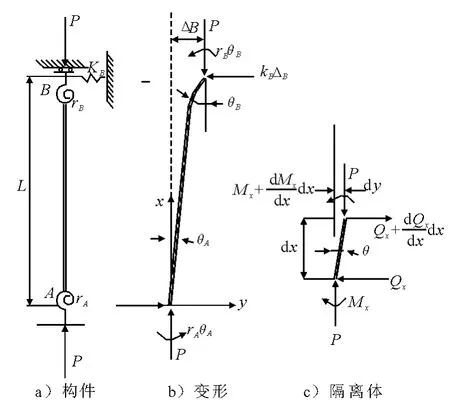
圖1 端部有約束的軸心受壓構件

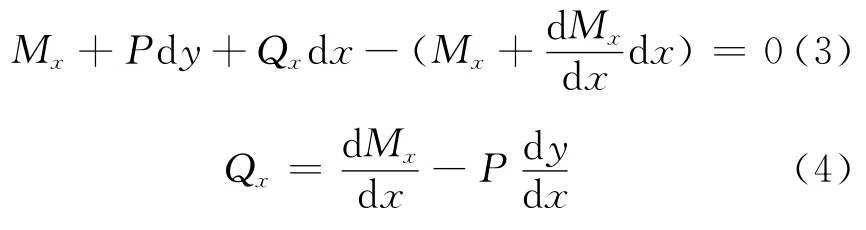
以式（4）代入式（2）后，得

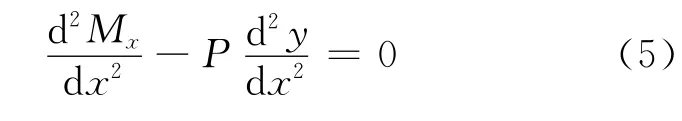
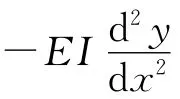
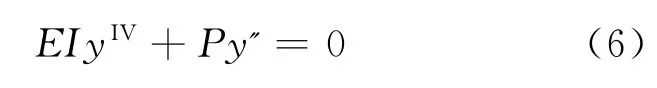
由式（4）又得到橫向力

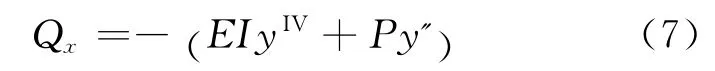
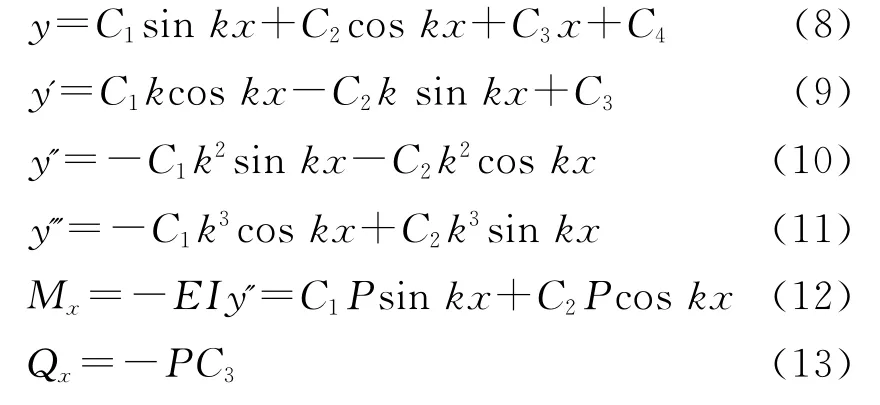
通解中的4個積分常數(shù)可由構件兩端的集合邊界條件和自然邊界條件確定，它們的表達式都可以用與構件的撓度y 有關的量來表示：（1）鉸接端，y＝0，Mx＝0或y＇＝0；（2）固定端，y＝0，y＇＝0；（3）自由端，Mx＝0或y＇＝0，Qx＝0或y＇＋k2y＇＝0；（4）上端只有平移的彈性約束，y＇（l）＝0，Q（l）＝－PC3＝－kBy（l）；（5）上端只有轉動的彈性約束，y（l）＝0，M（l）＝－EIy＇（l）＝rBy＇（l）；（6）上端有平移的彈性約束同時還有轉動的彈性約束，－C3P＝－kBy（l），－EIy＇（l）＝rBy＇（l）.

根據(jù)構件兩端的4個獨立的邊界條件可以建立4個線性齊次方程，組成如下線性方程組

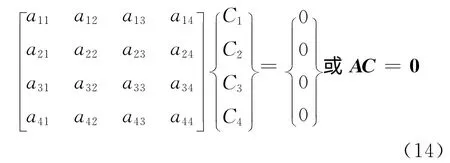
式中：a11，a12，…，a44均是取決于兩端邊界條件的系數(shù).由于式（13）中沒有常數(shù)項，因此C1，C2，C3，C4有非零解的條件是系數(shù)行列式為零，即

由于在式（14）中只有未知量k，所以P＝k2EI，從而可以解得P.但是式（14）的展開式是一個超越方程，適合此方程的解可能有很多個，應取其中的最小值為屈曲載荷Pcr.由于以上計算方法無直接的理論聯(lián)系，本次研究將不采用這種方法，而是采用軟件進行模擬節(jié)點銷接處理，來求得理想的彈性屈曲荷載的方法.

2 腳手架有限元建模

2.1 腳手架模型

本文從腳手架整體中選取一個雙排六步三跨的局部結構進行有限元建模，單元選用Ansys中的Beam188 三維梁單元.立桿步距（立桿高度）2.8m，縱距（2立桿間縱向X 距離）2.5m，橫距（2立桿間橫向Y 距離）2m.圖2為腳手架及其基本組件的有限元模型.組件之間的銷接節(jié)點通過耦合自由度的方式模擬，組件內部的焊接節(jié)點則通過共用節(jié)點的方式模擬，通過兩者的結合來模擬該腳手架的混合連接方式.

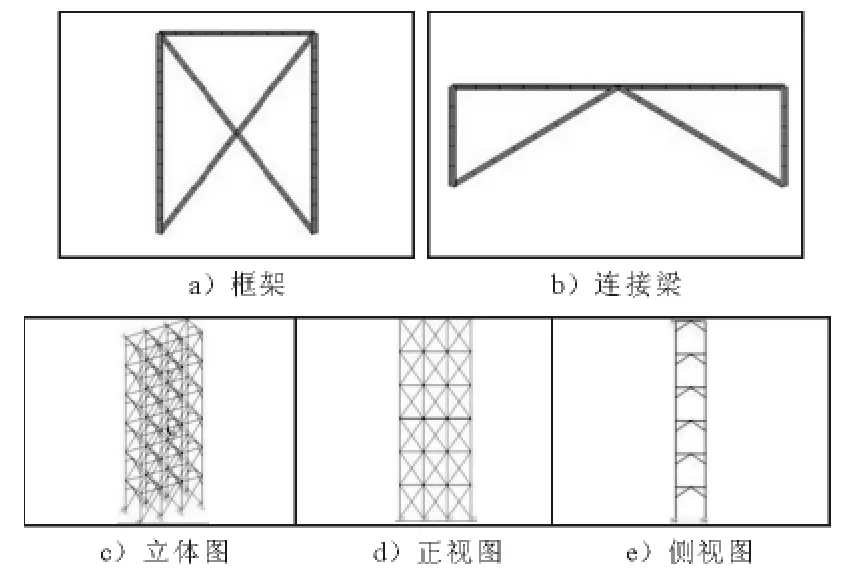
圖2 腳手架有限元模型

腳手架所用材料為低碳鋼Q235，常溫下的材料特性見表1.垂向立桿為薄壁構件，截面為空心方框，外邊長為80mm，厚度為5mm.

表1 構件材料特性

2.2 基本假設

應用有限元法，計算該腳手架的失穩(wěn)形式與極限穩(wěn)定承載力時，采用的假設有：（1）線彈性假設，腳手架各立桿與梁的軸線都在同一平面內；（2）數(shù)值相等的豎向集中荷載作用于框架頂層的各節(jié)點上；（3）忽略地震荷載、風荷載，以及動力載荷的影響；（4）在同一層中各立桿會同時發(fā)生屈曲.

3 失穩(wěn)形式與極限承載力分析

3.1 各種失穩(wěn)形式與極限承載力

分析該腳手架結構的前4階屈曲模態(tài)，計算腳手架在各階失穩(wěn)狀態(tài)下的極限承載力，見表2.

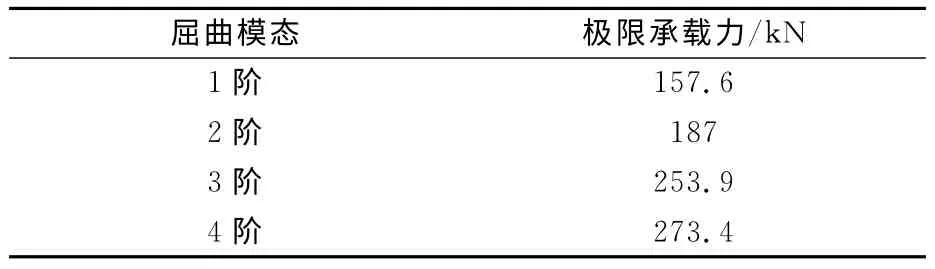
表2 不同失穩(wěn)形式下的極限承載力

典型的1 階失穩(wěn)最先發(fā)生在底層，見圖3a）.3階失穩(wěn)最先發(fā)生在第二層，向上下延伸，只有半個波形，見圖3c）.4階失穩(wěn)最先發(fā)生在中間層，出現(xiàn)2個完整的正弦波形，見圖3d）.前2階屈曲模態(tài)屬于局部失穩(wěn)，后2 階屬于整體失穩(wěn).

3.2 極限承載力影響因素

1）立桿縱距與步距的影響 取一系列的立桿縱距和立桿步距，分別計算該腳手架的極限承載力值，見表3～4.

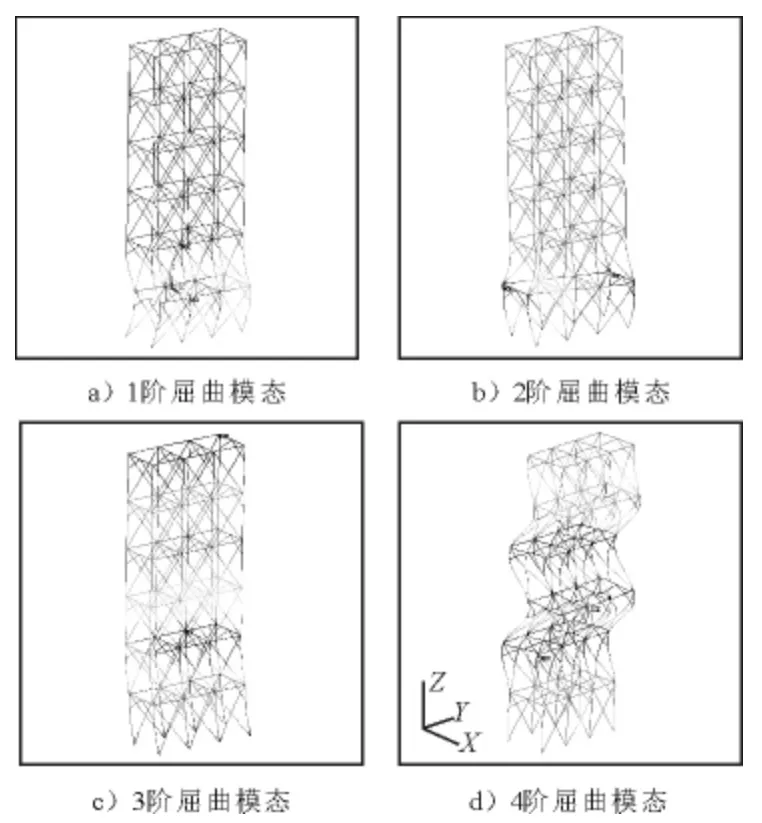
圖3 4種失穩(wěn)形式比較

表3 立桿縱距變化時極限承載力值

表4 立桿步距變化時極限承載力值

可以看出，極限承載力隨著步距和縱距尺寸的增加呈下降趨勢.通過比較下降趨勢，可以發(fā)現(xiàn)：步距對極限承載力的影響要大于縱距的影響.

2）步數(shù)的影響 表5所列為不同步數(shù)下的極限承載力，隨著步數(shù)的增加，腳手架的極限承載力不斷減小.

表5 步數(shù)變化時極限承載力值

3）連墻件位置的影響 連墻件三步一設和兩步一設時的極限承載力分別為197kN 和236 kN，比連墻件只設在頂部時的157.6kN 分別大25%和50%，說明連墻件的設置能夠大幅提高腳手架結構的極限承載力.屈曲模態(tài)圖見圖4～5，可以發(fā)現(xiàn)連墻件能有效防止連墻件以上的各層發(fā)生屈曲.值得注意的是這些連墻件都設置在結構較弱的橫向位置，對于縱向作用不大.

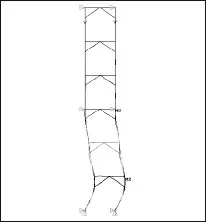
圖4 連墻件兩步一設

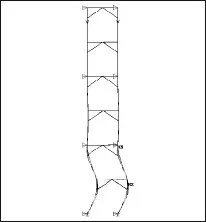
圖5 連墻件三步一設

3.3 承載力比較

根據(jù)文獻［6］中所列出的立桿的穩(wěn)定性公式算得同尺寸下扣件式腳手架的極限承載力為86.4 kN，與該混接式腳手架時的一階彈性屈曲極限承載力值157.6kN 進行比較，發(fā)現(xiàn)該類腳手架的極限承載力超過扣件式腳手架82%，值得推廣使用.將極限承載力除以立桿的截面積1500mm2，折算成鋼管所受的壓應力為105.1 MPa，而材料Q235的屈服強度為235MPa，故此結構在材料未達到屈服強度時已發(fā)生屈曲.

4 結 論

1）腳手架失穩(wěn)有多種形式，通常失穩(wěn)是沿它的橫向發(fā)生破壞的；該腳手架的失穩(wěn)主要發(fā)生在第一層和第二層，應對這2層進行加固處理.

2）腳手架與墻的橫向拉結有助于整體穩(wěn)定性的提高；立桿縱距增大時，極限承載力減小趨勢近似線性，立桿步距增大時，極限承載力呈非線性減小.

3）通過對比得出該腳手架極限承載力比扣件式腳手架高出82%.當屈曲發(fā)生時，材料尚未屈服.

［1］徐崇寶，張鐵錚，潘景龍，等.雙排扣件式鋼管腳手架工作性能的理論分析與實驗研究［J］.哈爾濱建筑工程學院學報，1989，22（2）：39－44.

［2］敖鴻斐.雙排腳手架整體穩(wěn)定極限承載力通用計算方法［J］.施工技術，2005，34（3）：39－41.

［3］WEESNER L B，JONES H L.Experimental and analytical capacity of frame scaffolding［J］.Engineering Structures，2001，23（6）：592－599.

［4］GODLLEY M H R，REALE R G.Sway stiffness of scaffold structures［J］.Structural Engineer，1997，75（1）：4－12.

［5］陳 驥.鋼結構穩(wěn)定理論與設計［M］.北京：科學出版社，2011.

［6］王玉龍.扣件式腳手架計算手冊［M］.北京：中國建筑工業(yè)出版社，2008.