基于協同神經網絡的導彈攻擊目標識別方法研究

郭 巍，張千宇，王光輝

（海軍航空工程學院 指揮系，山東 煙臺 264001）

復雜背景下軍事目標（飛機、軍艦、坦克等）的自動識別，不要求其輸出結果是一幅完整的圖像本身，而是將圖像經過某些處理后，再進行圖像分割和特征提取，從而進行解決分類。這類問題屬于模式識別的范疇，常采用經典的模式識別方法，主要是統計模式分類和句法（結構）模式分類。近年來新發展起來的模糊模式識別和人工神經網絡模式分類在圖像識別中也越來越受到重視。

二十世紀八十年代末，德國著名數學家、理論物理學家赫爾曼·哈肯（Herman Haken）教授提出了模式識別的新概念——協同模式識別（Synergetic Pattern Recognition，SPR）[1-2]，從自上而下的角度出發，描述了協同模式識別基本方程的構造原理，并提出了一個重要的觀點：模式識別的過程即為模式形成的過程。

協同模式識別從整體上分析目標的特征，識別過程符合人類的感知機制，以哈肯教授為核心的研究小組將協同模式識別用于2D工業零件識別[3]、手寫體字符識別、3D圖像校正和立體視覺中的視差計算等，取得了一些實踐結果，另外一些研究人員試圖解決圖像分割問題或構造基于協同學原理的聯想記憶模型。德國斯圖加特大學的Banzhaf教授等人對協同競爭學習機制作了深刻的研究[4]。

在國內，也有不少學者對協同模式識別進行了大量的研究，上海交通大學從1977年起，對協同理論進行了多方面深入而有意義的研究工作[5]。而合肥工業大學也從2000年開始，對協同模式識別等內容進行了從理論方法到實際應用各方面較為深入的研究工作[6]。另外北京師范大學、重慶大學等高校也先后不同程度的對協同理論方法與應用進行了研究[7-8]。

1 目標識別協同神經網絡的實現

1.1 協同神經網絡的構成

文獻[1]給出了用于協同識別的動力學模型，我們可以用一種并行的神經網絡算法進行求解：

式（5）中，γ為迭代步長，離散協同神經網絡的穩定性將主要取決于γ的大小。于是，Haken網絡可以轉化為圖1所示的類似三層前向網絡的形式，只是中間層序參量按式5動力學方程進行演化。

圖1 協同神經網絡的結構Fig.1 Structure of the synergetic neural network

1.2 協同神經網絡的運行步驟

協同神經網絡的運行過程包括兩個階段：首先是網絡的學習訓練階段，然后是網絡的識別階段。具體運行步驟如圖2所示。

圖2 協同神經網絡具體運行步驟Fig.2 Process of the synergetic neural network

1.3 協同神經網絡穩定性分析

文獻[2][8]分別從權矩陣特征值非負及勢函數的穩定最小點等方面詳細討論了連續協同神經網絡具有全局穩定性，這里不再贅述。離散協同網絡的穩定性與該網絡的迭代步長有很大關系。步長過大，會導致各個序參量的變化過于劇烈，而偏離原來的穩定軌道，使網絡呈發散狀態，導致系統無法完成識別功能。

通常來說，只要步長取得足夠小，就能保證系統收斂，但從下面的分析可以看出，序參量ξk的變化范圍及幾何分布情況隨著原型模式與待識別模式的變化有很大差異，要想找到一個在任何情況下都能保證系統穩定收斂的固定步長將很困難，即便能夠滿足要求，其識別速度及效率也將大幅度降低。為了避免在訓練過程中不至于出現太大的競爭波動，在這里對步長γ進行分析，以保證協同離散網絡能夠快速、穩定地收斂。

綜上所述，為保證系統應對每一模式均收斂，當ξ2k（n）取最小值0時，亦應收斂，因此離散協同神經網絡的迭代步長γ應滿足：

2 仿真研究

綜上所述，整個識別流程如圖3所示。

圖3 目標識別流程圖Fig.3 Flow chart of the target recognition

取10個飛機圖像作為訓練樣本，圖像大小為，每張圖片可以用一個4 096維向量描述，這些向量就是訓練樣本的原型模式vk，這里一共有10個樣本，訓練樣本的原型模式如圖4所示。

圖4 訓練樣本的原型模式Fig.4 Prototype pattern of the training sample

則原型模式分別對應的伴隨模式v+k如圖5所示。

圖5 原型模式對應的伴隨模式Fig.5 Adjoint model corresponging the prototype pattern

1）待識別樣本只是在訓練樣本的基礎上進行加噪，沒有發生平移、旋轉或者伸縮時，如圖6所示。

圖6 待識別圖像Fig.6 Picture to be identified

我們不需要對其進行不變性處理，直接輸入到協同神經網絡中進行識別。按照穩定性分析方法，取時能夠得到快速穩定的序參量收斂曲線，識別的形成過程如圖7所示。

圖7 識別的形成Fig.7 Target recognition's formation

此時的序參量及勢函數演化為：

2）當待識別樣本圖像只是訓練樣本殘缺的基礎上進行 加噪，也沒有發生平移、旋轉或者伸縮變化，如圖9所示。

圖8 序參量及勢函數演化曲線Fig.8 Evolution curve of the order parameter and potential function

圖9 殘缺的待識別模式Fig.9 Incomlete pattern to be recognized

我們不需要對其進行不變性處理，直接輸入到協同神經網絡中進行識別。同樣取得到識別的形成如圖10所示。

圖10 待識別模式殘缺時模式的形成Fig.10 Pattern s formation incomlete pattern to be recognized

此時的序參量及勢函數演化曲線：

從而可以看出，協同神經網絡對于殘缺的待識別模式同樣具有很好的有效性。

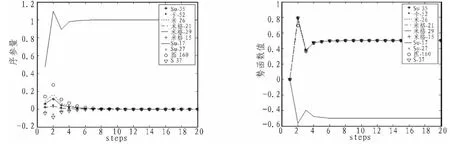
圖11 待識別模式殘缺時序參量及勢函數演化曲線Fig.11 Evolution curve of the order parameter and potential function incomlete pattern to be recognized

3 結束語

文中論述了協同學理論在模式識別中的應用，介紹了基本的協同識別模型及其算法框架；介紹了協同神經網絡并對其運行步驟和穩定性進行了分析；使用協同神經網絡相結合對軍事目標的識別進行了研究；最后并通過MATLAB對該方法在目標識別中的應用進行了仿真。

[1]Haken H.協同計算機和認知——神經網絡的自上而下方法[M].楊家本，譯.北京：清華大學出版社，1994.

[2]Daffershofer A，Haken H.Synergetic computers for pattern recongnition——A New Approach to Recognition of Deformed Patterns[J].Pattern Recognition，1994，27（12）：1697－1705.

[3]Wang F Y，Fever P J A，Pu B.A robotics vision system for object identification and manipulation using synergetic pattern recognition[J].Robot.Comput.Integrated Manufacturing，1993，10（6）：445－459.

[4]Banzhaf W，Schmutz M.Some Notes on Comperirion Among Cell Assemblies[J].Int’l Journal of Neural Systems，1992，2（4）：303－313.

[5]HU Dong-liang，QI Fei-hu，LIU Jian-feng.Recognition of objects with shew distortion based on synergetics[J].Pattern Recongnition Letters，1999（20）：255－265.

[6]Jun Gao，Jie Bao，Dingguo Chen.Optical-electrotronic Shape Recognition System Based on Synergetic Associative Memory.Proceedings of SPIE Applications of Artificial Neural Networks in Image ProcessingⅥ[C].San Jose，USA：Jan.2001，4305：138－148.

[7]吳渝.小波多分辨率分析模型研究與協同計算機[D].重慶：重慶大學，1997.

[8]鄭南寧.計算機視覺與模式識別[M].北京：國防工業出版社，1998.