Yx橡膠密封圈密封性能研究

夏衛明，駱桂林，嵇寬斌

（揚力集團 江蘇國力鍛壓機床有限公司，江蘇 揚州 225009）

0 引言

Yx 橡膠密封圈以其結構簡單、安裝方便、密封性能好等優點廣泛應用于液壓、氣動等密封場合。采用有限元手段對密封圈的研究較多，其中主要集中在 O 形密封圈[1-4]、A 形防塵圈[5]、X 形變截面密封圈[6]等，而關于Yx 密封的研究國內外報道較少。經檢索，楊光，胡旭林[7]等應用有限元分析了Y 形密封圈在不同工作壓力下的變形規律，但其密封圈的模型結構過于簡單，其唇部沒有按照Yx 密封圈的國家標準[12]進行建模分析，有限元分析中沒有計算安裝壓縮效果，這與實際有一定的差異；于潤生，楊秀萍[8]應用超彈性理論和非線性理論，采用有限元方法對Yx 形液壓密封圈的性能進行模擬，分析其失效的位置和模式，研究了參數對密封性能的影響，提出結構優化模型等等。這些專家學者的分析研究工作取得了一定的理論和工程應用價值。

本文應用ANSYS 有限元軟件對Yx 橡膠密封圈進行建模，研究了該型密封圈初始預壓縮量、工作壓力變化等對密封性能的影響和原因。

1 Mooney-Rivlin材料模型

Yx 橡膠密封圈采用的是TPU 聚氨酯材料，工程上主要是以連續介質力學為基礎，橡膠材料被認為是超彈性近似不可壓縮體（泊松比趨近于0.5），其力學性質表現為材料非線性和幾何非線性。目前，大型有限元軟件可以用來模擬超彈性材料的材料模型有：Neo-Hookean、Mooney-Rivlin、Ogden、Polynomial Form、Arruda-Boyce、Gent、Yeoh、Blatz-Ko 等，本文采用廣泛應用的Mooney-Rivlin 模型描述橡膠材料的應變能函數。

本文采用2 參數的Mooney-Rivlin 模型，其應變能函數表達式為：

其中，I1、I2為第一和第二Green 應變不變量，C10、C01為 Mooney-Rivlin 材料參數，d 為材料不可壓縮參數，由式d=（1-2n）/（C10+C01）給出，n 為材料泊松比。本文參照文獻[10]，取 C10、C01分別為 1.84MPa、0.47MPa。

2 有限元模型

根據Yx 密封圈、孔軸、密封溝槽邊界條件以及ANSYS 的功能，Yx 密封圈的有限元模型簡化為平面對稱模型，Yx 密封圈截面結構及尺寸參照國家標準JB/ZQ 4265-1997[12]進行建模，本文按公稱內徑為d=300mm 的軸用Yx 密封圈建模，彈性模量取為7.8MPa，泊松比為0.5（不可壓縮材料）。密封圈的硬度相對于金屬材料的軸、孔，非常之小，軸、孔的變形相對密封圈可以忽略不計，因此以剛體-柔體的面-面接觸單元TARGE169-CONTA172 來模擬Yx 密封圈對軸和溝槽的非線性接觸行為，橡膠單元采用帶中間節點的平面PLANE183 超彈性單元來模擬（ANSYS 較早的版本采用 HPPER56，HPPER74 等超彈性單元），設置單元關鍵字KEYOPT（3）=2 來模擬平面應變（Plane strain）問題。如圖1 所示。

3 預壓縮計算

YX 密封圈裝入溝槽中，其唇口與軸和溝槽內壁形成一定的預壓縮形成的回彈力給密封接觸面一定的壓力，達到密封的作用。按照密封圈的結構尺寸，其預壓縮量[12]為d=1.63～2.3mm，活塞桿的配合公差為f 8，直徑d=300mm 的活塞桿，其單邊誤差范圍為 0.028 ～0.068mm，基本上可以忽略。因此，分別取δ=1.63、1.8、2.3mm 三種情況進行分析比較，得到von Mises應力云圖如圖 2、3、4 所示（應力單位：MPa，變形比例因子：1）。

分析可知，在無液體壓力作用下，預壓縮量的變化對Yx 密封圈的應力分布的影響不大，預壓縮量增大0.63mm，最大von Mises 應力只增加了約0.3MPa，主要是由于密封圈之類橡膠柔性材料，其彈性模量很小，按應力應變公式，s=Ee，其變形量e 對應力的影響相對很小。

在預壓縮量加大的情況下，Yx 密封圈上唇口變形量比下唇口大，預壓縮量為2.3mm 時，上唇口基本被壓縮為直線，與溝槽內壁基本貼合，而下唇口還基本維持點接觸狀態（三維模型為線接觸），上唇口剛度小于下唇口。分析可知，下唇口與軸外圓柱面之間有相對運動，Yx 密封圈的這種變形方式有利于減小運動摩擦力，減緩密封圈的磨損，提高使用壽命。

在預壓縮量為 δ=1.63、1.8、2.3mm 三種情況下，下唇口與軸外圓柱面的最大接觸壓力分別為1.52、1.67、2.28MPa，接觸壓力基本按壓縮量成線性遞增，這是因為下唇口與軸外圓柱面接觸面積基本維持線接觸不變，壓縮量增加與施加的擠壓力成正比。

4 工作壓力計算

Yx 密封圈質地相對斯特封、格萊圈等組合形式的密封圈要柔軟，在高壓的作用下容易被擠入活塞桿和缸筒之間的間隙中。因此，Yx 密封圈一般用在活塞缸的桿腔，或反向安裝在活塞頭下端，用來對低壓進行密封（液壓缸回程壓力一般小于最大工作壓力），我公司生產的液壓機床最大液壓工作壓力為25MPa，因此，本文的計算按0～25MPa，以1MPa 為載荷步增量逐步增加，計算中取標準預壓縮量δ=1.8mm。取26 個載荷步，時間增量為1s，共計算26s。本文所研究的對象為靜態分析，時間設置并非真正意義上的時間，使用時間的目的在于使用ANSYS 的時間歷程后處理器，查看Yx 密封圈下唇口尖點處接觸壓力隨工作壓力的變化規律。設置第一個載荷步的時間TIME=1，第2～26 個載荷步的時間逐步增加1，第2～26 個載荷步以重啟動方式求解，以便生成時間歷程記錄文件，便于進行時間歷程后處理。

第1 個載荷步計算預壓縮，工作壓力為零，第2～26 個載荷步計算液壓工作載荷，每個載荷步壓力增量1MPa。工作壓力的計算采用循環方式求解，以減小程序的長度，該部分的命令流如下。

P=1

*DO，K，1，25，1

CMSEL，S，LOAD_NODE ! 選擇加載節點組

SF，ALL，PRES，P+（K-1） ! 壓力每次增加 1MPa

TIME，K ! 設置時間

NSUBST，200，2000，10

KBC，0

CNVTOV，U，，0.05，2，0.01 ! 位移收斂允差

CNVTOV，F，，0.02，2，0.01 ! 力移收斂允差

ALLSEL，ALL

SOLVE

*ENDDO

*SET，K

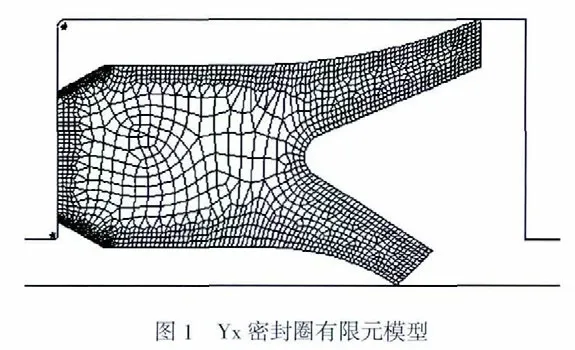
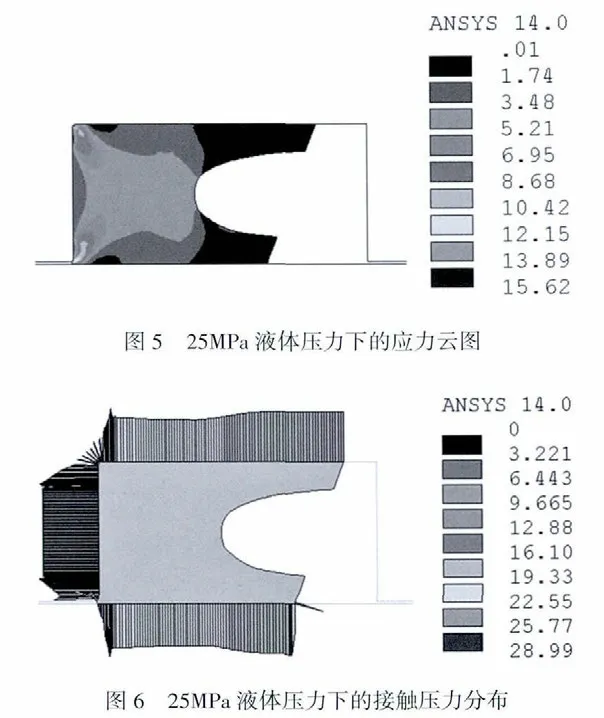
如圖5 所示是液體壓力為25MPa 時，Yx 密封圈橫截面的應力分布云圖，最大應力約為15MPa，產生在溝槽下口圓角（R=0.2mm）接觸區。整個密封圈外側完全和溝槽內壁以及軸圓柱面緊密貼合，有少量被擠入軸孔之間的間隙中，接觸線上的接觸壓力分布也較為均勻，如圖6 所示，除了拐角處變化較大，接觸線上的接觸壓力大體在22～26MPa 之間分布。

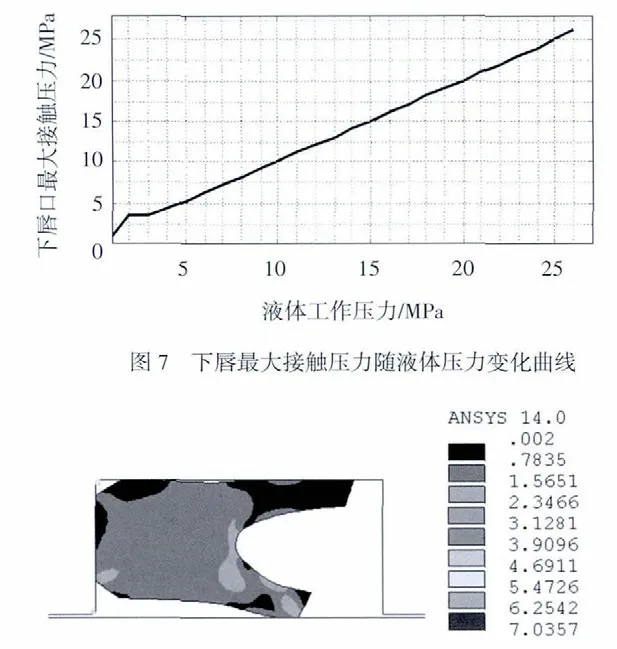
關于密封圈的失效準則和失效判據，目前普遍采用密封面最大接觸壓力大于液體工作壓力來判斷。圖7 是Yx 密封圈下唇口處最大接觸壓力隨工作壓力的變化曲線。分析可知，在液體工作壓力為0～2MPa 時，下唇口最大接觸壓力增加較快，此時接觸壓力為3.65MPa，這是因為此時下唇口基本還處于點接觸狀態，見圖8。液體壓力2～3MPa 時，下唇口最大接觸壓力增加的速度減慢，到約為5MPa 以后，下唇口最大接觸壓力基本隨液體工作壓力的增加而線性增加。

取Ratio=下唇口最大接觸壓力/液體工作壓力之比值。其意義為，當Ratio>1 時，密封良好，當Ratio<1，有滲漏。繪制成Ratio-液體工作壓力曲線圖如圖9 所示，液體壓力為零時，Ratio→∞，這與實際情況是完全吻合的。在液體壓力約為0～3MPa 時，Ratio下降較快，液體壓力約3MPa 以后下降速度減慢，約為5MPa 以后逐漸水平。分析整個曲線，在整個加載區間，Ratio>1，說明密封情況良好。因此，分析可知，Yx 密封圈的低壓密封效果較高壓密封效果要好，高壓狀態并不能增加密封性能的判據Ratio 值，相反，高壓狀態下，由于整個密封圈變形較大，增大了接觸面積和接觸壓力，從而增加運動件的運動阻力，加快了密封圈的磨損。因此在設計密封結構時，一般應將Yx 密封圈放置在低壓側，有利于提高使用壽命和密封性能。

當然這在理論是符合的，實際生產的Yx 密封件由于材料，制作工藝等差別，以及被密封零件結構的形狀尺寸誤差，低壓下的貼緊效果并不是很理想。實踐表明，進口密封圈的低壓密封效果要遠遠優于國產密封圈。據了解，我公司的進口密封圈主要采用的是高壓注塑成型工藝，成型件材料致密度高，冷卻收縮率小，精度保持性好。而大部分國產密封圈采用的澆鑄成型工藝，容易形成局部氣孔、夾雜、收縮等缺陷，低壓下容易出現滲漏現象。

5 低壓狀態細化計算

前述工作壓力的計算研究的是Yx 密封圈在0～25MPa 液體工作壓力下的密封狀態，計算中取的液體工作壓力載荷步增量為1MPa，相對較大，為了更精確研究Yx 密封圈在低壓下的工作狀態，現取液體工作壓力為0～5MPa，以0.1MPa 為一個載荷步增量，重新計算。得到下唇最大接觸壓力隨液體壓力變化曲線圖和下唇口Ratio 值隨液體壓力的變化曲線圖，如圖 10、11 所示。

載荷步細化計算表明，在液體工作壓力約為0.7MPa 時，下唇口最大接觸壓力達到一個峰值，以后逐漸降低，在液體壓力約為1.3MPa 時為另外一個拐點，在此區間內，下唇口最大接觸壓力隨液體工作壓力的增加而逐步遞減，約3MPa 以后，又近似成線性遞增，Ratio 值也成近似線性遞減。

為了便于解釋這種現象，這里引入變形速率的概念，取橡膠密封圈的變形速率g=e/s，s為橡膠密封圈內某點的應力，e 為該點在應力為s 下產生的變形量。該值表達了材料在不同應力作用下的變形能力。

分析曲線圖10 可知，Yx 密封圈下唇口的最大接觸壓力出現了兩個分界點。

初始狀態下，Yx 密封圈在軸孔的擠壓和約束作用下形成一定的預壓縮量，從而產生下唇口的初始最大接觸壓力，隨著液體工作壓力的逐步增加，密封圈產生的變形越來越大，下唇口與軸外圓柱面的接觸面積也逐步增大，在液體壓力為0.7MPa 時，接觸壓力與接觸面積的比值大到一個極值點，也即在0.7MPa 液體工作壓力以內，下唇口的變形速率逐漸減小，0.7MPa 時降低到第一個分界點，此時下唇口部分的材料變形很小，主要變形集中在接觸尖端（對平面模型來說）。0.7～1.3MPa 下唇口變形速率逐漸增大，1.3MPa 到達極值點，在此區間內，下唇口附近的材料開始向軸內側彎曲，使得下唇口接觸線長度增加。1.3MPa 以后，下唇口變形速率又逐漸減小，此時雖然液體工作壓力增加了，但接觸壓力增加卻相對緩慢，主要是下唇口的彎曲變形能力減小了。約為3MPa 以后，Ratio 值基本趨近于1，再增加液體工作壓力，Yx 密封圈的下唇口大部段貼合在密封表面，其變形能力明顯降低。當液體壓力增加到將Yx 密封圈擠壓到完全貼合溝槽內壁和被密封的表面時，其變形速率為零，此時，再增加液體壓力，密封圈接觸線附近的單元不會產生形變，密封間隙處除外。

6 下唇口接觸線長度計算

分析可知，在液體工作壓力為0～1.3MPa 區間內，Yx 密封下唇口變形不穩定，密封接觸線變形規律不穩定。根據我公司液壓機設計制造多年的經驗，液壓缸多出現低壓滲漏，活塞桿在低壓回程時容易出現掛油現象，這一方面與Yx 密封圈和被密封的液壓缸零部件的制造精度有關，另一方面也與Yx密封圈下唇口在進行密封時接觸線的變化規律有關。下文將從不同液體壓力下對Yx 密封圈下唇口密封接觸線的變化規律方面入手，探索接觸線的變化對Yx 密封圈密封性能的影響。

為了得到足夠高的計算精度，將接觸線處的單元進行細化處理，細化后的單元邊長只有0.03mm左右，這足以保證發生接觸部分的接觸線長度計算精度。

計算中，取 0～10MPa 液體壓力，取 201 個載荷步，第1 個載荷步計算預壓縮，第2～201 個載荷步計算液體工作壓力，載荷增量為0.05MPa，以重啟動方式循環求解。

計算接觸線長度的主要思想是：取Yx 密封圈下唇口與軸圓柱面上會產生接觸的單元，通過ANSYS 的通用后處理器的單元表功能取得各接觸單元接觸壓力表，通過與數組結合，逐個單元地判斷接觸壓力是否為零，將接觸壓力非零的單元和對應的單元編號賦予新的數組中，再定義數組取得所有單元節點的X 坐標，使用冒泡排序法對節點X 坐標數組進行排序，找到X 坐標值最大和最小的發生接觸的節點，取這兩節點X 坐標值NX 和其X 方向的變形量UX，則節點變形后的坐標NX′=NX+UX，將兩節點的NX′相減，得到接觸線長度值DIS_UX=NX2′-NX1′。給出該部分的計算命令流如下，以供參考。

FINISH

/POST1

LOADSTEP_NUM=201 ! 載荷步工況數

*DIM，DIS_UX，ARRAY，LOADSTEP_NUM，1

*DO，K，1，LOADSTEP_NUM，1

ETABLE，ERASE

SET，K ! 讀取第K 載荷步結果數據

CMSEL，S，CONTAT_ELEM ! 選擇下唇口接觸單元組

ETABLE，CONT_PRES，CONT，PRES

*GET，ENUM，ELEM，0，COUNT !計算單元數量

*GET，EMIN，ELEM，0，NUM，MIN ! 取最小單元編號

*DIM，EN_STORE，ARRAY，ENUM，1 ! 存儲單元編號

*DIM，PR，ARRAY，ENUM，1 ! 存儲單元壓力

*DIM，ES，ARRAY，ENUM，1

COUNTER=0 ! 計數器

N=1

*DO，I，1，ENUM，1

EN_STORE（I，1）=EMIN

*GET，PR （I，1），ELEM，EN_STORE （I，1），ETAB，CONT_PRES

*IF，PR（I，1），NE，0，THEN

COUNTER=COUNTER+1 ES（N，1）=EN_STOR E（I，1）

N=N+1

*ENDIF

EMIN=ELNEXT（EMIN）

*ENDDO

*SET，I

*DIM，ENUM_CON，ARRAY，COUNTER，1

*DO，I，1，COUNTER，1

ENUM_CON（I，1）=ES（I，1）

*ENDDO

*SET，I

ESEL，S，，，ENUM_CON（1，1）

*IF，COUNTER，GT，1，THEN

*DO，I，2，COUNTER，1

ESEL，A，，，ENUM_CON（I，1）

*ENDDO

*ENDIF

*SET，I

EPLOT

NSLE，S，1

NPLOT

*GET，NNUM，NODE，0，COUNT ! 計算節點數量

*GET，NMIN，NODE，0，NUM，MIN ! 取最小節點編號

*DIM，NN_STORE，ARRAY，NNUM，1!存儲節點編號

*DIM，NNX，ARRAY，NNUM，1 !存儲節點 X 坐標

*DO，I，1，NNUM，1

NN_STORE（I，1）=NMIN

NNX（I，1）=NX（NN_STORE（I，1））

NMIN=NDNEXT（NMIN）

*ENDDO

*SET，I

!! 找出X 坐標最大和最小的節點編號

!! 冒泡法排序，升序排列

!! 同時節點編號數組對應更新

*DO，I，1，NNUM-1，1

*IF，NNX（I，1），GT，NNX（I+1，1），THEN

TEMP1=NNX（I，1）

NNX（I，1）=NNX（I+1，1）

NNX（I+1，1）=TEMP1

TEMP2=NN_STORE（I，1）

NN_STORE（I，1）=NN_STORE（I+1，1）

NN_STORE（I+1，1）=TEMP2

*ENDIF

*ENDDO

NODE_XMINNUM=NN_STORE（1，1）

NODE_XMAXNUM=NN_STORE（NNUM，1）

!! 計算變形后接觸線長度，將各工況

!! 下接觸線長度放入數組DIS_UX

NODX1=NX（NODE_XMINNUM）

NODX2=NX（NODE_XMAXNUM）

NUX1=UX（NODE_XMINNUM）

NUX2=UX（NODE_XMAXNUM）

DIS_UX （K，1）=（NODX2+NUX2）-（NODX1+NUX1）

*ENDDO

得到Yx 密封圈下唇口接觸線長度隨液體工作變化曲線圖如圖12 所示。

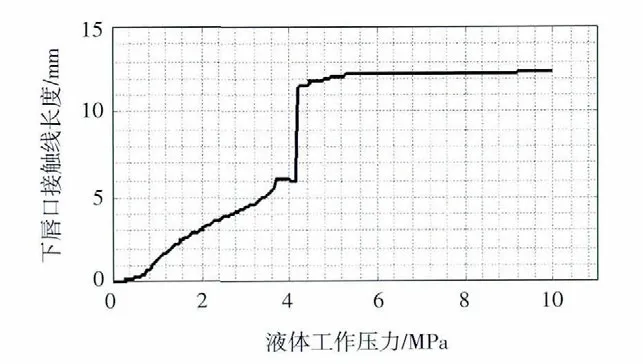
圖12 下唇口接觸線長度隨液體壓力的變化

分析該曲線，在液體壓力約為0.7MPa 時曲線處產生了第一個拐點，在此范圍內接觸線長度增加速度緩慢，證實了前文所述的Yx 密封圈下唇口最大接觸壓力變化曲線的第一個分界點。以后接觸線長度隨工作壓力的增加逐步上升，在液體壓力為3.7～4.2MPa 之間出現了一段水平線，此時的接觸線長度約為6mm，見圖13。在此液體工作壓力區間內，密封接觸線長度穩定，形成最佳密封效果。液體壓力超過4.2MPa，接觸線長度階躍式增大到約為11mm，此時密封圈的下部基本與軸外圓柱面相接觸了。說明4.2MPa 是接觸線變化的一個重要分界點，液體工作壓力再增加，接觸線長度不再增加，顯而易見，是因為此時密封圈下唇口已近幾乎和被密封表面完全貼合了。

圖13 液體壓力為4MPa 的X 向變形云圖

因此，筆者認為，Yx 密封圈最佳的密封工作壓力約為3.7～4.2MPa，當然，此值是基于本文所取的材料參數而言，Yx 密封圈在制作時其材料參數不可能絕對統一。此時，Yx 密封圈下唇口密封接觸線長度穩定，與運動件的接觸面積相對較小，對密封圈的磨損相對減弱。

7 負工作壓力計算

液壓機的滑塊在作快速下行運動時，主缸上腔會形成一個負壓，以吸開安裝在主缸尾部大孔中的充液閥，主缸通過充液閥補油，滿足其快速下行流量的需要，該壓力一般在0.03MPa 左右。另一方面，由于液壓缸的工作介質液壓油中常常會混入空氣形成氣泡，在液體工作壓力變化時，氣泡的破裂會產生局部負壓，因此對負壓條件下的Yx 密封圈工作狀態的計算很有必要。

本文取0.03MPa 的負壓，按初始預壓縮量0～2.3mm，以0.1mm 為一個載荷步增量進行計算，繪制成下唇口最大接觸壓力與預壓縮量之間關系的曲線圖，如圖14 所示。

圖14 0.03MPa 負壓下下唇口最大接觸壓力隨預壓縮量的變化

Yx 密封圈在0.03MPa 負壓下，預壓縮量為1.2mm 時，下唇口最大接觸壓力開始增加，預壓縮量小于1.2mm，預預壓縮量的變化對下唇口最大接觸壓力幾乎無影響。

8 結論

本文應用有限元方法建立了Yx 密封圈的有限元模型，分析了預壓縮量、工作壓力對Yx 密封圈密封性能的影響及其下密封唇口的接觸壓力變化規律。得出結論為，在不考慮制造誤差情況下，從理論上講，Yx 密封圈的低壓密封效果較高壓密封效果要好，高壓狀態并不能增加密封接觸壓力的判據Ratio值。高壓狀態下，由于整個密封圈變形較大，增大了接觸面積和接觸壓力，從而增加運動件的運動阻力，加快了密封圈的磨損。因此在設計密封結構時，一般應將Yx 密封圈放置在低壓側。本文的研究為工程設計提供了理論依據。

重點分析了低壓條件下，Yx 密封圈的工作狀態。低壓條件下（平面模型），Yx 密封圈的下唇口變形速率隨液體壓力的變化出現了兩個分界點，第一個分界點是Yx 密封圈下唇口接觸尖端的點接觸變形到線接觸變形的轉折點。第二個分界點是下唇口線接觸變形速率最大的轉折點，液體壓力超過1.3MPa，下唇口變形速率減小。

對Yx 密封圈密封線長度隨液體工作壓力的變化的計算表明，液體壓力在3.7～4.2MPa 時，密封接觸線長度相對穩定，此時的密封接觸線長度約為6mm，該壓力為Yx 密封圈穩定工作的最佳值。超過此壓力，Yx 密封圈的下唇口大部分段將和被密封表面接觸，使得接觸線長度階躍式增長到接近其下唇口的會發生接觸的最大接觸線長度（14mm）。該液體工作壓力值（3.7～4.2MPa）對工程設計提供了依據。

在0.03MPa 的負壓下，預壓縮量大于1.2mm時，下唇口的最大接觸壓力開始緩慢線性增加。

[1]鐘 柱，陳 軍，等.液壓伺服作動器密封圈的有限元分析[J].潤滑與密封，2010，19：31-35.

[2]李振濤，孫鑫暉，等.O 形密封圈密封性能非線性有限元數值模擬[J].潤滑與密封，2011，（9）：86-90.

[3]尚付成，饒建華，等.超高液壓下O 形橡膠密封圈的有限元分析[J].液壓與氣動，2010，（1）：67-70.

[4]Sidra Cohen，E.P.Muntz.An experimental study of rotating micromechanical liquid O-ring pressure seals [J].Sensors and Actuators A：Physical，Volume 54，Issues 1-3，-June 1996，Pages 765-774.

[5]高新陵，楊 帆，等.A 型橡膠防塵圈密最大接觸應力與唇形變化的敏感性分析[J].2011，24（10）：113-115.

[6]劉占軍，王哲峰.X 形變截面優化橡膠密封圈比較應力有限元分析[J].潤滑與密封，2010，（1）：56-58，77.

[7]楊 光，胡旭林，等.Yx 形密封圈應力與變形非線性有限元分析[J].煤礦機械，2010，（3）：99-101.

[8]于潤生，楊秀萍.Yx 形液壓密封圈的有限元分析及結構優化[J].潤滑與密封，2011，（7）：66-69，74.

[9]諶 彪，張贊牢，等.靜密封條件下Y 形橡膠密封圈有限元分析[J].潤滑與密封，2009，（3）：72-75.

[10]譚 晶，楊衛民，等.O 形橡膠密封圈密封性能的有限元分析[J].潤滑與密封，2006，（9）：65-69.

[11]T.Tussman，K-J Bathe.A Finite Element Formulation for Nonlinear Incompressible Elastic and Inelastic Analysis [J].Computers and Structures，Vol.26 Nos 1/2，1987，pp.357-409.

[12]JB/ZQ 4265-1997，軸用Yx 形密封圈.

[13]沈林健，奚偉民，等.液壓機活塞桿表面滲漏油分析及防止措施[J].鍛壓裝備與制造技術，2008，43（2）：48-49.

[14]范玉林，張營杰，等.45/50MN 快鍛油壓機本體結構設計分析[J].鍛壓裝備與制造技術，2011，46（2）：24-25.