基于直方圖平移的醫學圖像可逆水印算法

劉 芳，金作林

(1.北京電子科技學院，北京 100070;2.第四軍醫大學，陜西 西安 710032)

醫學圖像水印技術是對醫學影像設備形成的數字化圖像或模擬圖像經量化后的數字化圖像，按照實際應用來隱藏秘密信息以滿足用戶需要的技術。在現代醫療體系中，醫學專家可以通過遠程健康診療系統，方便快捷地獲取病人的醫學圖像來診斷病情。為了便于專家的診斷，同時保護病人的隱私，確保醫學圖像的版權，大量的水印信息，如病人信息、相關診斷數據、醫院的標識、醫生的簽名等需要秘密嵌入供診斷的醫學圖像中。因此，醫學圖像水印算法的優劣，將直接影響使用者對圖像的最終感受，進而影響到對圖像的理解和對疾病的診斷。目前的圖像水印算法大多屬于有損水印，水印信息嵌入的同時會導致載體圖像產生永久的失真，主要用于圖像產品的版權保護和認證，并不完全適用于醫學圖像這類特殊的應用。在此背景下，可逆圖像水印技術成為了近年來的研究熱點之一，被廣泛應用于醫學、軍事、司法、政務等領域。

所謂可逆水印，是指在正確提取水印后還能無損地恢復原始圖像的水印技術。從應用角度來看，可逆水印更加適用于隱秘信息傳輸和脆弱性認證。

已有的可逆圖像水印算法可以分為3類:1)基于無損壓縮的方法［1－4］。此類算法容易實現，但嵌入數據量較小。2)基于差值擴展的方法［5－7］。此類算法利用可逆整數小波變換，將秘密信息嵌入擴展后的高頻小波系數(像素對差值)中，水印的嵌入對圖像質量的影響較大。3)基于直方圖平移的方法［8－10］。此類算法根據圖像特征首先構建直方圖，然后找到直方圖中的峰值點和零值點，通過直方圖平移修改將水印嵌入在具有峰值點特征的像素中。其優點是水印不可見性好，計算簡單，但缺點是允許嵌入的水印量依賴于圖像特征的分布。

對于醫學圖像而言，在保證可逆性的同時減少圖像失真遠比增加水印容量更重要。因此本文的研究就是結合醫學圖像的特點，從改進水印不可見性的角度提出了一個基于分塊的灰度直方圖平移水印算法。

1 灰度直方圖平移

Ni算法［8］描述了直方圖平移方法的基本原理。首先構建圖像的灰度直方圖，在直方圖中找到峰值點(圖像中出現次數最多的像素數目)和零值點(圖像中出現次數最少的像素數目，一般為出現次數為零的像素數目)。用p表示峰值點，z表示零值點，z＞p，記錄p和z的值，如圖1a所示。然后將圖像中所有灰度值處于區間［p+1，z－1］的像素的值加1，即將區域［p+1，z－1］內的直方圖向右平移一位，使得灰度值為p+1的像素個數為0，如圖1b所示。嵌入水印時，如果水印為“1”，則灰度值為p的像素的值加1，變為p+1;如果水印為“0”，則保持不變，如圖1c所示。提取水印時，根據記錄的p和z的值，掃描圖像。若像素的灰度值為p，其攜帶的水印位為“0”，若像素的灰度值為p+1，其攜帶的水印位為“1”。提取水印后，只需將灰度值處于區間［p+1，z］的像素的值減1，即可恢復原始圖像。

圖1 直方圖平移方法示意圖

顯然，直方圖越陡峭，則水印嵌入容量越高;而需平移的像素點數量越少，則圖像失真越小，水印不可見性越好。一般來說，醫學圖像的灰度取值范圍較窄，峰值點的分布相對比較集中。以圖2a為例，將其劃分為8×8的塊，則峰值點的分布如圖3所示。可以看出，圖像中的峰值點集中分布在少量分塊中。如果嵌入和提取水印時能夠識別峰值點的位置，僅在峰值點所在的分塊而不是整個圖像進行直方圖平移操作，就可以在不影響算法可逆性的條件下，大大減少需平移像素點的個數，從而獲得更好的圖像質量。

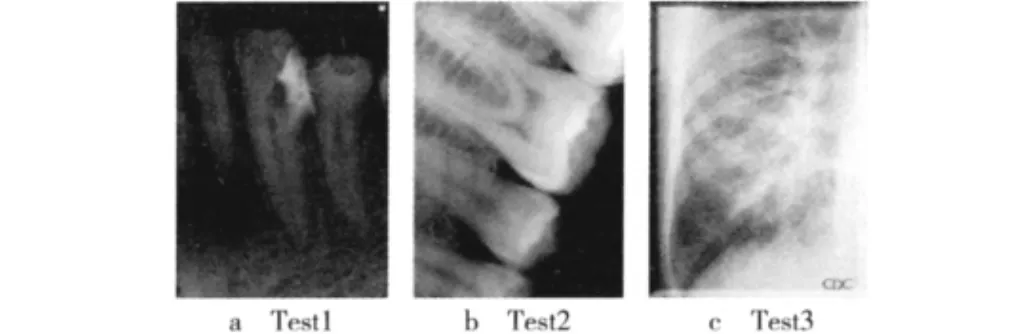
圖2 原始圖像

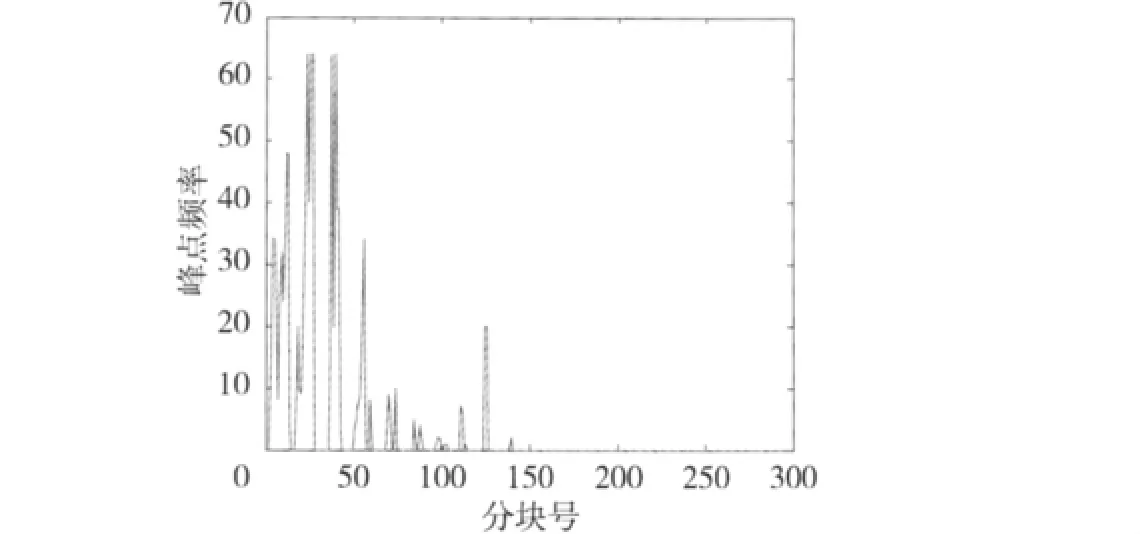
圖3 峰值點分布圖

2 水印嵌入算法

假設原始圖像 I大小為M×N，每個像素x∈［0，255］。w 為二值水印序列，w∈{0，1}。

嵌入算法的步驟描述如下:

1)構建圖像I的灰度直方圖，記錄峰值點p和零值點z。如式(1)所示，hist(x)是圖像的灰度直方圖

步驟1，統計圖像塊內峰值點(值為p的像素)的個數count_p。判斷count_p是否大于0，如果count_p＞0，轉入步驟2;反之，轉入步驟4。

步驟2，嵌入水印，如式(2)所示

步驟3，判斷當前塊嵌入的水印序列是否全為1。如果全為1，則嵌入后的圖像塊內不含峰值點，設定標志位flag(k)=1，k=k+1。

步驟4，統計圖像塊內值為p+1的像素的個數count_p1，如果count_p1=0，跳過當前塊;反之，設置flag(k)=0，k=k+1。

4)整合所有圖像塊，得到嵌入水印后的圖像I'。

為了能夠在提取水印后無損地恢復原始圖像，數據嵌入的過程中，需要存儲一定長度的輔助信息。對于本文算法來說，輔助信息包含三部分內容:一是峰值點和零值點，共16位;二是分塊標志位，共k－1位，可以采用行程編碼對其進行無損壓縮;三是記錄上/下溢出的相關信息，其長度取決于溢出點的個數。本文算法中，溢出現象只可能發生在灰度值為0和255的像素上。假設原像素的值x=0，如果調整x的值，使x=x－1，則出現下溢。同理，假設x=255，如果使x=x+1，則出現上溢。可以采用簡單的直方圖收縮技術來處理溢出。對于取值為0和255的像素，修改其值，使之變為1和254，并記錄溢出位置。

3 水印提取和圖像恢復算法

水印提取和圖像恢復算法的步驟描述如下:

1)對于待測圖像進行分塊，每個分塊的大小為s×t。標志位計數器k初始值為1。

步驟1，統計圖像塊內峰值點(值為p的像素)的個數count_p。判斷count_p是否大于0，如果count_p＞0，轉入步驟2;反之，轉入步驟4。

步驟2，提取水印，即

步驟3，提取水印后，恢復圖像，即

步驟4，統計圖像塊內值為p+1的像素個數count_p1，如果count_p1=0，跳過當前塊;反之，如果flag(k)=1，調用式(3)和式(4)提取水印和恢復圖像，k=k+1，如果flag(k)=0，跳過當前塊，k=k+1。

3)整合所有圖像塊，得到提取水印和恢復后的原始圖像。

4 實驗結果

實驗編程環境采用MATLAB7.0，Windows XP操作系統，1 Gbyte內存。實驗中使用的二值水印序列隨機產生，3幅測試醫學圖像從網絡圖像庫中選取，如圖2所示。

1)水印不可見性

選定分塊大小為8×8，在圖2的測試圖像中嵌入最大容量水印，得到的含水印圖像如圖4所示，其對應的PSNR如表1所示。實驗結果表明，嵌入最大容量水印后，圖像質量較好，PSNR可達到56 dB以上，水印不可見性好。

圖4 含水印圖像

表1 含水印圖像質量

2)水印容量

利用本文算法進行水印嵌入時，實際的水印嵌入容量R應為總容量C減去輔助信息長度L的值，即

由于掃描圖像進行水印嵌入的過程中，每遇到灰度值等于峰點p就會嵌入1 bit信息。因此，C即為p的出現頻率。可見，C值越大，L值越小，水印的實際嵌入容量越大。

表2顯示了在分塊大小為8×8的情況下，不同測試圖像的實際嵌入容量。實驗結果表明，容量大小與圖像特征有關。圖像紋理越簡單，容量越大;反之，容量越小。

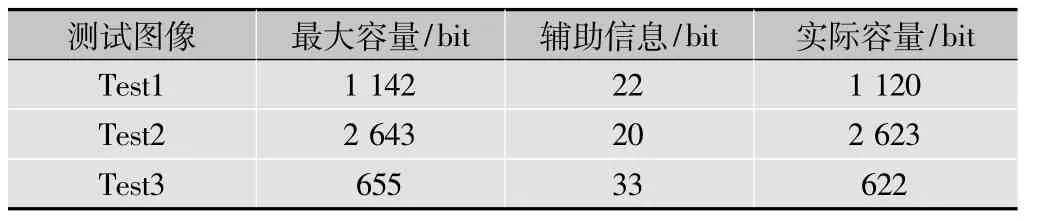
表2 實際嵌入容量

3)計算復雜度

本文算法屬于空間域算法。計算開銷主要來源于產生直方圖、尋找峰值點零點、掃描圖像嵌入水印、直方圖平移等操作。假設載體圖像大小為M×N，對于本文算法而言，在嵌入水印的過程中需要對圖像進行兩輪掃描，第一輪產生直方圖，第二輪嵌入水印的同時進行直方圖平移，因此計算復雜度為O(2MN)。

4)分塊大小的選取對算法性能的影響

值得注意的是，分塊大小的不同對圖像質量和水印容量可以產生影響。表3顯示了分塊大小分別4×4，16×16時，得到的含水印圖像的PSNR及實際嵌入容量。可以看出，分塊越小，圖像質量越好，容量越低;反之，圖像質量越差，容量越高。

表3 分塊大小對算法性能的影響

5 結論

本文從提高水印不可見性的角度提出了一種基于直方圖平移的醫學圖像可逆水印算法。該算法的缺點是輔助信息過多，嵌入容量有限。下一步將研究如何盡可能地壓縮輔助信息，并將算法的思想應用于差值直方圖平移算法，在保證高質量的同時進一步擴充可隱藏容量。

本文算法屬于脆弱性水印算法，可以應用到信息隱藏、圖像認證和重要圖像的保密傳輸等安全領域。

［1］HONSINGER C W，JONES P，RABBANI M，et al.Lossless recovery of an original image containing embedded data:US，6278791［P］.2001－08－21.

［2］FRIDRICH J，GOLJAN J，DU R.Invertible authentication ［C］//Proc.SPIE Security and Watermarking of Multimedia Content 2001.［S.l.］:SPIE，2001:197－208.

［3］CELIK M U，SHARMA G，TEKALP A M.Lossless watermarking for image authentication:a new framework and implementation［J］.IEEE Trans.Image Processing，2006，15(4):1042－1049.

［4］李書欣，王泉，吳延贊，等.基于HVS感知模型與數據壓縮的可逆圖像水印算法［J］.電視技術，2010，34(6):26－27.

［5］TIAN J.Reversible data embedding using a difference expansion［J］.IEEE Trans.Circuits and Systems for Video Technology，2003，13(8):809－896.

［6］ALATTAR A M.Reversible watermark using the difference expansion of a generalized integer transform［J］.IEEE Trans.Image Processing，2004，13(8):1147－1156.

［7］WENG S W，ZHAO Y，PAN J S.Reversible data hiding using the companding technique and improved DE method［J］.Circuits Systems and Signal Processing，2008，27(2):229－245.

［8］NI Z，SHI Y Q，ANSARI N，et al.Reversible data hiding［J］.IEEE Transa.Circuits and Systems for Video Technology，2006，16(3):354－362.

［9］TSAI P，HU Y C，YEH H L.Reversible image hiding scheme using predictive coding and histogram shifting［J］.Signal Processing，2009，89(6):1129－1143.

［10］LUO HAO，YU F X.Reversible data hiding based on block median preservation［J］.Information Sciences，2011，181(2):308－328.