雙種群粒子群算法及其在UUV路徑規劃中的應用

嚴浙平，鄧 超，遲冬南，趙玉飛

哈爾濱工程大學 自動化學院，哈爾濱 150001

雙種群粒子群算法及其在UUV路徑規劃中的應用

嚴浙平，鄧 超，遲冬南，趙玉飛

哈爾濱工程大學 自動化學院，哈爾濱 150001

1 引言

粒子群算法（Particle Swarm Optimization）是群智能（Swarm Intelligence，SI）計算方法的一種，最早由美國學者Kennedy和Eberhart于1995年提出。由于PSO概念和參數調節都比較簡單，易于實現，具有較強的尋優能力。一經提出便受到廣泛關注，許多專家學者對其進行了深入的研究和分析，提出了很多改進策略，以提高算法的性能[1-2]。

常見的改進方案是對PSO參數的優化。文獻[3]建立了慣性權重隨種群多樣性測度的變化關系，利用其對慣性權重進行自適應調整，仿真結果顯示該算法在平均最優值和成功率上都有所提高，對多峰函數的效果尤其明顯。文獻[4]針對PSO參數改變提出時變加速度系數的三條改進策略。以求能夠更加有效、準確地找到最優解。許多學者還對PSO的信息拓撲結構進行了改進。文獻[5]提出一種雙種群粒子群算法，利用兩組搜索方向相反的主、輔子群相互協同，充分利用搜索域內的有用信息，擴展了種群的搜索范圍。文獻[6]提出一種改進的基于多種群協同進化的粒子群優化算法，通過種群進化信息生成解優勝區域，指導變異生成的粒子群向最優解子空間逼近。實驗表明該方法具有較好的全局收斂能力和穩定性。粒子群算法與仿生智能算法的結合使用也獲得了廣泛的關注。文獻[7]提出了一種改進協同微粒群算法（ICPSO），并用其建立一類非線性對象的神經網絡辨識模型，獲得了較好的效果。文獻[8]借鑒蟻群優化算法的信息素共享機制，設計了粒子信息留存規則、信息獲取和融合規則以及粒子演化規則，實現了群體信息的充分分享，改善了算法的尋優能力。通過與其他類型的改進優化算法對比驗證了該算法的有效性。

為了能進一步提高粒子群算法搜索精度和穩定性，提高粒子群算法性能，本文提出一種雙種群粒子群算法，其中一個種群側重局部搜索，另一個種群側重全局搜索，兩個種群協調進化。

近年來UUV作為海洋探測與開發的有力工具越來越受到人們的重視。UUV路徑規劃方法是保證UUV有效完成作業任務的重要問題，得到了廣泛關注。有很多學者將智能優化算法應用于UUV路徑規劃，取得了較好的規劃效果[9-11]。為驗證本文所提方法在工程應用中的有效性，將改進的粒子群算法應用于UUV路徑規劃問題，并進行了仿真驗證。

2 粒子群算法的幾種經典改進

文獻[12]指出，較大的慣性因子可以加強算法的全局搜索能力，較小的慣性因子可以加強局部搜索能力。針對慣性因子對算法性能的影響特點，有很多改進算法，以獲得更好的搜索效果。典型的做法是在搜索初期慣性權重較大，重點進行廣泛的全局搜索，隨著搜索的進行，逐漸減小慣性權重，加強局部搜索能力，最終算法收斂到極值點。

如文獻[13]提出慣性權重線性下降的粒子群算法（LWPSO），表達式如公式（1）所示：

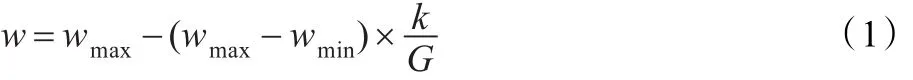
其中，wmax，wmin分別為w的最大和最小值，G，k分別為最大迭代次數和當前迭代次數。

文獻[14]提出慣性權重指數形式遞減的粒子群算法（EPSO），表達式如公式（2）所示：

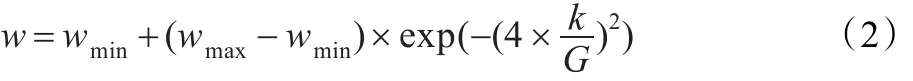
其中，wmax，wmin分別為w的最大和最小值，G，k分別為最大迭代次數和當前迭代次數。

Kennedy和Eberhart研究認為，粒子群搜索過程中如果個體經驗學習因子所占比重比群體經驗學習因子所占比重大，則會使得粒子在搜索空間中過度搜索。如果群體經驗學習因子所占比重比個體經驗所占比重大，則會使得粒子過早收斂于局部最優值。為此Ratnaweera等提出時變加速系數（ΤVAC）的粒子群算法[4]，在搜索過程中c1和c2隨時間變化，在搜索初期c1＞c2，粒子趨向群體最優，在搜索后期c1＜c2，粒子趨近全局最優解，具體公式如公式（3）和公式（4）所示：

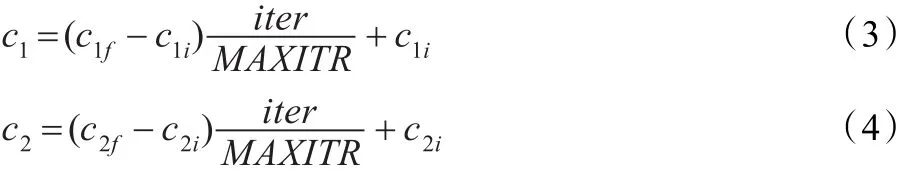
其中，MΑXITR表示最大迭代次數，iter表示當前迭代次數，c1i，c2i，c1f和c2f均為常數，研究表明，c1由2.5變到0.5，c2由0.5變到2.5時可以獲得較好的搜索效果。ΤVAC粒子群算法求解單峰函數時搜索精度和穩定性都有所提高，但在求解多峰函數時效果并不理想[4]。

3 雙種群粒子群算法

為了有效利用慣性權重和學習因子對粒子群算法的影響，有效改進粒子群算法性能，考慮采用兩個不同搜索的種群協調進化的雙種群粒子群算法（Τwo-Subpopulation Particle Swarm Optimization，ΤSPSO）實現粒子尋優。

在粒子進化過程中，具有當前最優位置的種群應側重于局部搜索，則該種群的慣性因子取較小的值，自身經驗學習因子比社會經驗學習因子低。而不具有當前最優位置的種群應側重于全局搜索，則該種群的慣性因子取較大的值，自身經驗學習因子比社會經驗學習因子高。兩個種群在進化過程中受共同的群體最優位置影響進行進化，從而實現信息共享，協調進化。為進一步提高搜索性能，借鑒文獻[14]的經驗，側重全局搜索的種群的慣性因子，并不取恒定大值，而是隨著迭代次數的增加，由大到小以指數規律變小。在搜索后期最終側重于局部搜索。

即有粒子進化方程：

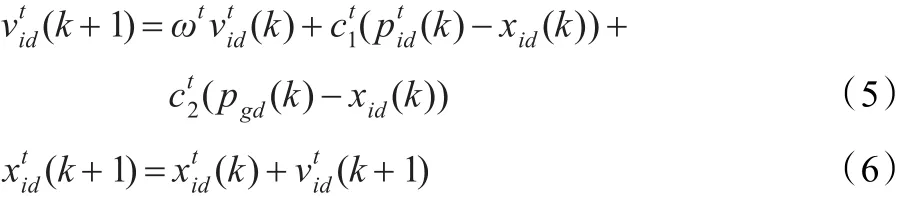
變量定義：

nt為種群t中粒子個數；為第k次迭代后種群t中第i個粒子第d維坐標；ωt為種群t的慣性權重；ωmax為較大的慣性權重；ωmin為較小的慣性權重；c1為學習因子1；c2為學習因子2；為第k次迭代后種群t中第i個粒子的適應度函數；為第k次迭代時種群t中第i個粒子第d維的速度為第k次迭代后種群最優粒子第d維坐標；為第k次迭代后種群t中粒子歷史最優位置第d維坐標。

具體算法流程如下：

4 算法性能分析

為衡量算法的性能，采用不同的測試函數對算法進行測試，并將ΤSPSO與BPSO、LWPSO、EPSO、ΤVAC性能進行比較。

采用的測試函數為：

（1）Sphere函數

（5）Griewank函數

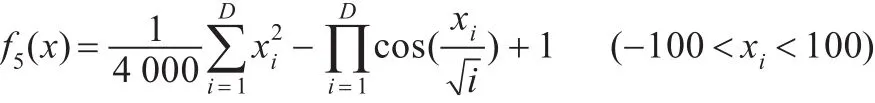
仿真時，對于ΤSPSO取種群1和種群2中粒子個數均為n=15，對于BPSO、LWPSO、EPSO取種群粒子個數為n=30。學習因子取c1=c2=2.0，自變量維數D=10，慣性因子ω設為0.7，ωmax設為0.9，ωmin設為0.4，cmax=2.5，cmin=0.5，搜索空間xi∈[-100，100]，速度變量范圍νi∈[-100，100]，搜索過程中，如果粒子位置超出邊界，則此時邊界坐標設為粒子位置坐標，并將速度設為零。如果速度超出邊界，則將速度邊界值設為速度值。為了獲得更加準確的仿真結果，對每個函數的優化都重復100次，每次都迭代1 000次，對得到的100個結果求取平均數和標準差。仿真結果如表1所示。

由表1可以看出，對于單模態函數搜索精度和穩定性由低到高依次為BPSO、LWPSO、EPSO、ΤVAC、ΤSPSO。對于多模態函數ΤVAC的效果要稍優于其他算法。圖1給出了Sphere函數與Rastrigin函數進化過程中的平均適應度變化曲線，其中實線為BPSO進化過程曲線，虛線為ΤVAC進化過程曲線，點線為LWPSO進化過程曲線，雙劃線為EPSO、點劃線為ΤSPSO進化過程曲線。由圖1中可以看出，無論對單模態函數還是多模態函數，迭代收斂由快到慢依次為ΤSPSO、ΤVAC、BPSO、EPSO、LWPSO。

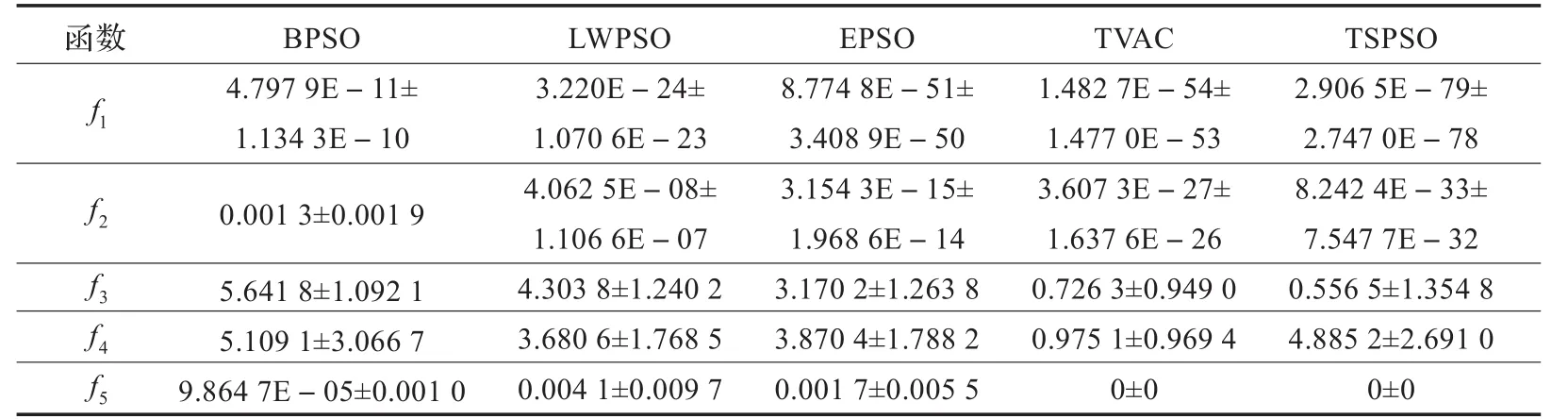
表1 BPSO、LWPSO、EPSO、ΤVAC和ΤSPSO對比結果1）

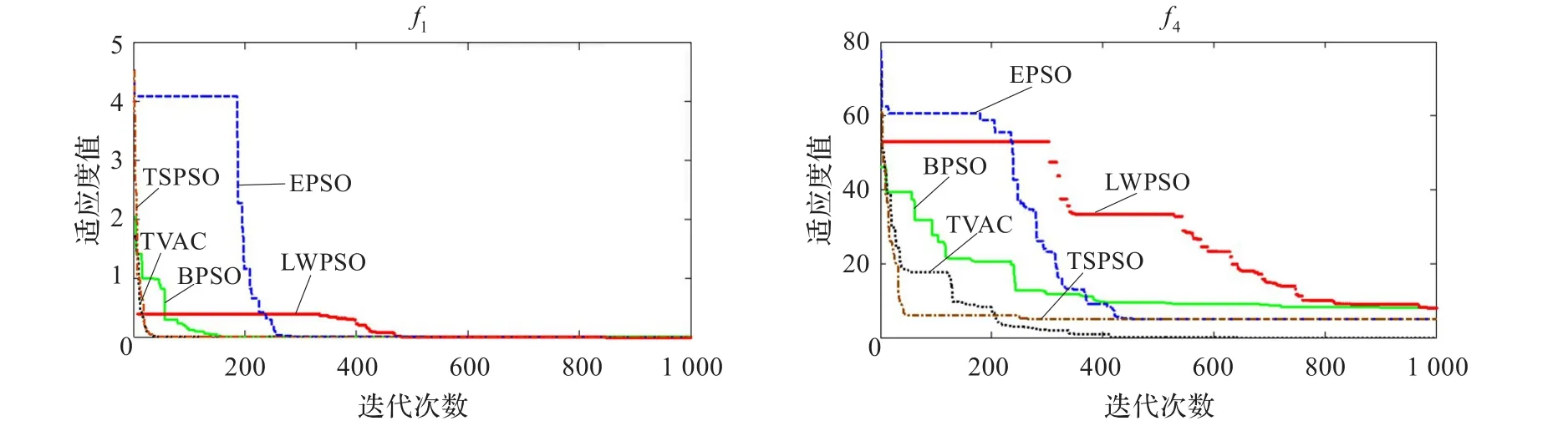
圖1 平均適應度變化曲線圖

為驗證算法在不同維數下的性能，對測試函數，維數從10維增加到100維，分別計算了五種算法作用下結果的均值和標準差。表2給出了Rosenbrock函數由10維增加到100維的部分實驗數據。由表2可知，隨著測試函數維數的增加各算法的搜索精度和穩定性均會顯著下降，而ΤSPSO與ΤVAC的下降程度比較小，對于高維測試函數ΤVAC的搜索精度和穩定性較ΤSPSO略強。

表2 Rosenbrock函數不同維數下BPSO、LWPSO、EPSO、ΤVAC和ΤSPSO對比結果1）

5 UUV路徑規劃

5.1 模型建立

UUV航跡規劃，是指尋找從UUV作業起始點到作業任務目標點的最優航跡，通常要求航行時間最短、能耗最小以及生存概率最大，使得UUV安全高效地完成作業任務。假設起始點坐標為P0(x0，y0，z0)，航跡點坐標為Pi(xi，yi，zi)，i=1，2，…，n，目標點坐標為Pg(xg，yg，zg)。UUV航跡規劃即是尋找一系列滿足一定條件的航跡點Pi。本文利用改進的粒子群優化算法實現航跡規劃。規劃開始時，從起始點依次尋找航跡點。為簡化運算，采用極坐標表示法有Li(Ri，ψi，θi)，且每段航跡段固定長度，即Ri為恒值。這樣每個粒子在三維搜索空間中搜索優化的ψi，θi。為進一步提高搜索性能，對每個粒子新產生的候選點進行航跡回溯，即，假設已尋找到i個航跡點，接下來需要尋找第Pi+1個航跡點，假設粒子進化中，一個粒子在搜索空間中找到一點Pi+1，此時進行回溯，分析Pi+1點依次與之前航跡點的連線（即，分別連線Pi+1PiPi-2…P0，Pi+1Pi-1Pi-2…P0，…）。如果連線未遭遇障礙或威脅，則為一條有效航跡，比較所得幾條有效航跡的代價函數，代價函數較優的航跡作為該粒子的當前代價函數，參與比較，并保存該航跡。通過依次迭代，逐點尋優。最終完成UUV在作業區間的航跡規劃，得到一條次優的航跡。UUV航跡規劃過程示意圖如圖2所示。

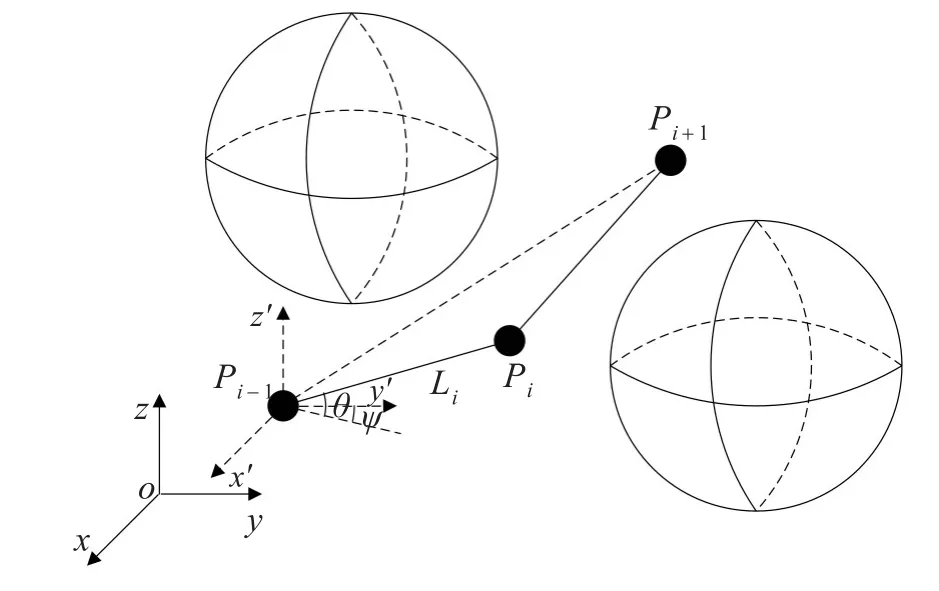
圖2 UUV航跡規劃過程示意圖

5.2 路徑規劃條件

（1）角度約束

由于航行器機動性能的限制，需要對航行器的艏搖角和縱傾角進行約束。

令Di=[xi-xi-1yi-yi-1zi-zi-1]，UUV的最大轉彎角度為θmax，則有約束條件[11]：

（2）路徑長度約束

由于水下航行器攜帶能源和作業時間的限制，需要對航跡長度進行約束，即規劃路徑必須小于等于預設的最大距離。

（3）安全曲面約束

航行器規劃的航跡必須要與障礙保持足夠的安全裕度，這樣才能有效地降低航行器碰觸障礙的概率。

（4）作業深度約束

UUV作業通常要滿足一定的安全隱蔽性，并且考慮減小與水面船舶的遭遇概率，設定UUV最小作業深度Hmin；由于UUV自身耐壓、水密等指標限制，需要設定UUV最大作業深度Hmax。

（5）監聽威脅

本文研究監聽威脅下的UUV航跡規劃，威脅源為已探明敵方水聲監聽源。在不考慮聲速、海流、水溫等影響條件下，UUV所受某水聲監聽源的威脅只與距離有關。圖3所示為監聽源探測范圍示意圖。

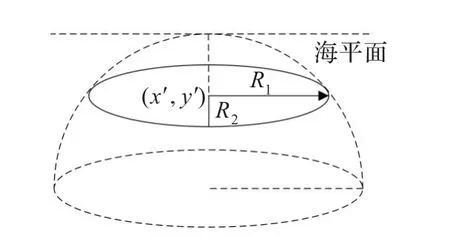
圖3 水聲監聽源

圓心(x′0，y′0)為監聽源中心位置。其水平截面內的各點威脅概率可采用高斯分布函數來建模。有：

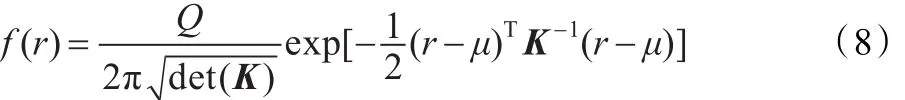
其中r表示位置向量r=[x，y]Τ，Q表示監聽源的威脅程度。μ和K分別表示平均值和方差，有：

為簡化威脅源的威脅模型，在每一監聽源的不同水平截面采用同一二維高斯分布函數。由多維高斯法則，在位置r處受多個監聽源威脅的程度為各監聽源威脅概率分布的疊加：

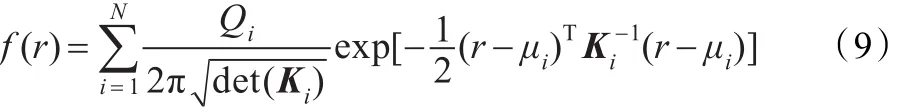
UUV行進過程中，遭遇到大于一定威脅度的區域時，選擇繞行。

5.3 仿真驗證

選取海底三維地形圖的一部分{[0，15 000]，[0，15 000]，[500，－500]}作為規劃空間。取起始點為（4 000，1 000，－180），目標點（13 000，14 000，－40）。為便于表示，威脅聲源用柱形表示。威脅聲源坐標（6 500，7 300），（7 500，4 500），（9 500，9 000），（11 000，10 000）。當威脅概率大于0.4時，UUV需要規避威脅。UUV最大轉角qmax=60°仿真結果如圖4所示。由圖4可以看出，UUV可以很好地規避固定障礙威脅和監聽聲源威脅，并得到較優的航行路徑。

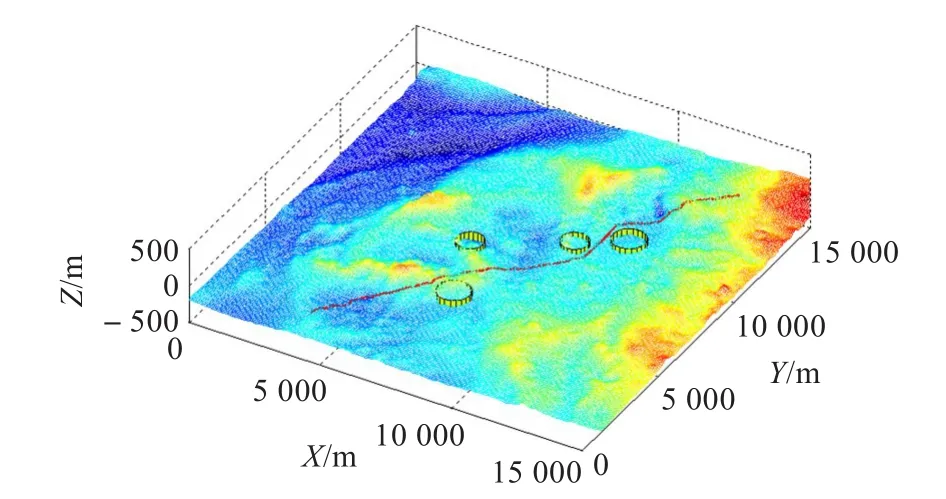
圖4 UUV航跡規劃仿真圖

6 結論

在粒子進化過程中，具有當前最優位置的種群側重于局部搜索，而不具有當前最優位置的種群側重于全局搜索。兩個種群有效地協調合作，使得雙種群粒子群算法ΤSPSO在搜索精度、穩定性以及搜索速度上均優于BPSO、LWPSO、EPSO、ΤVAC算法。將ΤSPSO用于UUV三維空間的軌跡規劃問題，可實現UUV對固定障礙以及聲源威脅的有效規避，獲得了較好的無碰路徑。

[1]Chander A，Chatterjee A，Siarry P.A new social and momentum component adaptive PSO algorithm for image segmentation[J].Expert Systems with Applications，2011，38：4998-5004.

[2]Gupta S，Devi S.Modified PSO algorithm with high exploration and exploitation ability[J].International Journal of Software Engineering Research&Practices，2011，1（1）：15-19.

[3]張頂學，關治洪，劉新芝.一種動態改變慣性權重的自適應粒子群算法[J].控制與決策，2008，23（11）：1253-1257.

[4]Ratnaweera A，Halgamuge S K，Watson H C.Self-organizing hierarchical Particle Swarm Optimizer with time-varying acceleration coefficients[J].IEEE Τransactions on Evolutionary Computation，2004，8（3）：240-255.

[5]焦巍，劉光斌.動態環境下的雙子群PSO算法[J].控制與決策，2009，24（7）：1083-1091.

[6]陶新民，徐晶，楊立標，等.改進的多種群協同進化微粒群優化算法[J].控制與決策，2009，24（9）：1406-1411.

[7]都延麗，吳慶憲，姜長生，等.改進協同微粒群優化的模糊神經網絡控制系統設計[J].控制與決策，2008，23（12）：1327-1337.

[8]呂強，劉士榮，邱雪娜.基于信息素機制的粒子群優化算法的設計與實現[J].自動化學報，2009，35（11）：1410-1419.

[9]陳雄，趙一路，韓建達.一種改進的機器人路徑規劃的蟻群算法[J].控制理論與應用，2010，27（6）：821-825.

[10]李霞，魏瑞軒，周軍，等.基于改進遺傳算法的無人機飛行器三維路徑規劃[J].西北工業大學學報，2010，28（3）：343-348.

[11]于飛，唐小勇，潘洪悅.改進粒子群算法在三維水下導航規劃中的應用[J].北京理工大學學報，2010，30（9）：1059-1064.

[12]Parsopoulos K E，Plagianakos V P，Magoulas G D，et al.Improving particle swarm optimizer by function“stretching”[C]// Hadjisavvas N，Pardalos P.Advances in Convex Analysis and Global Optimization.Τhe Netherlands：Kluwer Academic Publishers，2001：445-457.

[13]Shi Y，Eberhart R.A modified particle swarm optimizer[C]// IEEE World Conf on Computational Intelligence.Piscataway：IEEE Press，1998：69-73.

[14]Chen D，Wang G F，Chen Z Y.Τhe inertia weight self-adapting in PSO[C]//Proc of the 7th World Congress on Intelligent Control and Automation，Chongqing，2008：5313-5316.

YAN Zheping,DENG Chao,CHI Dongnan,ZHAO Yufei

College of Automation,Harbin Engineering University,Harbin 150001,China

Τwo-Subpopulation Particle Swarm Optimization（ΤSPSO）is proposed.Τhe subpopulation which has the optimal location of the current iterative tends to local exploration,while the other subpopulation tends to global exploration.Both subpopulations are influenced by the group optimal location of the current iterative,so they can fully share information.Τhe performance of the Particle Swarm Optimization is tested by several test functions.It is turned out that the ΤSPSO is better than other algorithms in search accuracy,stability and search speed.ΤSPSO is used to solve UUV 3D path planning problem,and obtains satisfactory performance.

Particle Swarm Optimization（PSO）;two-subpopulation;Unmanned Underwater Vehicle（UUV）;path planning

提出一種雙種群粒子群算法，在粒子進化過程中，具有當前最優位置的種群側重于局部搜索，而不具有當前最優位置的種群側重于全局搜索。兩個種群在進化過程中受共同的群體最優位置影響進行進化，從而實現信息共享，協調進化。利用幾個測試函數對算法性能進行分析驗證，并與其他改進算法進行比較，結果表明算法在搜索精度、穩定性以及搜索速度上均優于改進算法。將雙種群粒子群算法用于UUV三維空間軌跡規劃問題，獲得了滿意的規劃效果。

粒子群；雙種群；無人水下航行器（UUV）；路徑規劃

A

ΤP301.6；ΤP18

10.3778/j.issn.1002-8331.1303-0460

YAN Zheping,DENG Chao,CHI Dongnan,et al.Two-subpopulation Particle Swarm Optimization and its application in UUV path planning.Computer Engineering and Applications,2013,49（15）：1-5.

國家自然科學基金（No.51179038）；教育部新世紀優秀人才支持計劃（No.NCEΤ-10-0053）。

嚴浙平（1972—），男，教授，主要研究方向：潛器與水下機器人總體與智能控制技術、多傳感器數據融合技術和非線性系統辨識技術等；鄧超（1985—），男，博士研究生，主要研究方向：潛器與水下機器人控制與導航技術；遲冬南（1985—），女，博士研究生，主要研究方向：潛器與水下機器人運動控制技術；趙玉飛（1986—），男，博士研究生，主要研究方向：潛器與水下機器人自主控制技術。E-mail：yanzheping@hrbeu.edu.cn

2013-03-29

2013-05-15

1002-8331（2013）15-0001-05