四點接觸球軸承摩擦力矩特性分析

陳龍，史朋飛，李正國，邱明，夏新濤

(河南科技大學 機電工程學院，河南 洛陽 471003)

1 概述

與深溝球軸承相比，四點接觸球軸承承載能力更高；與角接觸球軸承相比，四點接觸球軸承可承受雙向軸向載荷；與成對雙聯角接觸球軸承相比，四點接觸球軸承的極限轉速高并且軸向竄動小[1-3]。由于四點接觸球軸承的一系列優點，故得到了廣泛的應用。大型轉盤軸承多采用四點接觸結構，依據承載能力高低要求，目前使用的四點接觸轉盤軸承有單排球結構、雙排同徑球結構和雙排異徑球結構等[4-7]。受裝配因素影響，小型四點接觸球軸承內圈或外圈需采用半圈結構，如QJF000型雙半外圈四點接觸球軸承(圖1a)和QJ000型雙半內圈四點接觸球軸承(圖1b)[8-9]；內、外圈為整體結構的四點接觸轉盤軸承(圖1c)則采用專門的裝球孔進行裝配[4]。小型四點接觸球軸承套圈材料一般采用GCr15，大型四點接觸球轉盤軸承套圈材料則采用50Mn或42CrMo[10]。小型四點接觸球軸承溝道加工時大部分采用修整砂輪切入磨削，大型四點接觸球轉盤軸承套圈采用切入磨削或數控硬車[11]。軸承溝道的加工誤差對于鋼球與溝道的接觸位置有著顯著影響，實際生產中大多采用刮色法檢測接觸位置，這種檢測方法不能進行定量檢測，也難以確定其實際接觸角[12-15]。實際接觸點位置的改變直接影響接觸角的大小，進而影響到四點接觸球軸承的游隙值[10, 15-19]及其內部的載荷分布狀態[5]。

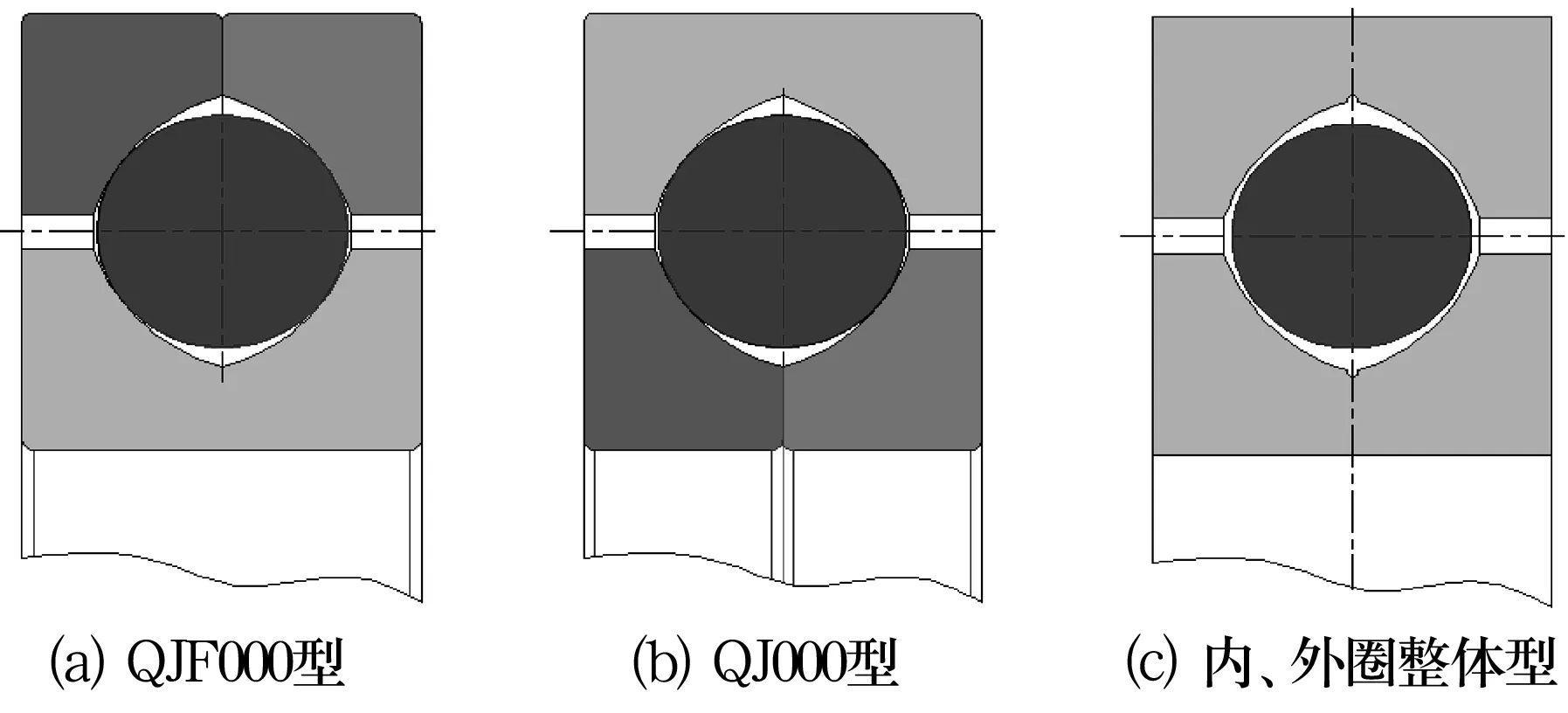
圖1 四點接觸球軸承的結構類型

摩擦力矩的大小決定了軸承的功耗和溫升，是軸承的一個重要性能參數。軸承摩擦力矩受眾多因素，如結構、設計、加工、摩擦、潤滑及使用條件等的影響[20-22]。

采用不同模型計算同型號軸承的摩擦力矩值，對比分析模型的差異，找出計算值差異的原因，有助于確定影響摩擦力矩的關鍵幾何因素。

2 摩擦力矩的理論計算模型

2.1 SKF的修正計算模型

對于四點接觸球軸承，SKF公司提出的修正摩擦力矩計算模型為[23]

M=φishφrsMrr+Ms1+Mseal+Mdrag，

(1)

(2)

式中：φish為切入發熱減少系數；φrs為貧油回填減少系數；Mrr為滾動摩擦力矩；Msl為滑動摩擦力矩；Mseal為密封件摩擦力矩；Mdrag為由于拖拽損失、渦流和飛濺等導致的摩擦力矩；Dpw為球組節圓直徑；n為軸轉速；ν為潤滑油動力黏度。此計算模型未考慮內部幾何參數對摩擦力矩的影響。

由于試驗選用了L61潤滑脂，故直接采用脂潤滑條件下的簡化模型，

(3)

Mrr=Grr(ν1n)0.6，

(4)

(5)

Msl=Gslμsl，

(6)

(7)

式中：D為軸承外徑；d為軸承內徑；ν1為潤滑劑在工作溫度時的運動黏度；Fr為徑向載荷；Fa為軸向載荷；μsl為滑動摩擦因數。

(5)式和(7)式中的Fr與Fa為外載荷。由(1)～(7)式可知，外形尺寸相同的四點接觸球軸承的摩擦力矩應一致，但實測數據卻相差很大。

2.2 考慮內部幾何結構參數的計算模型

產生摩擦力矩的根本因素在于內、外圈與鋼球之間的相互運動。由于此類軸承一般裝用較高精度的鋼球，即鋼球精度比溝道精度要高，故下面研究溝道精度對于軸承摩擦力矩的影響。

Florin T提出了考慮軸承內部幾何結構參數的四點接觸球軸承摩擦力矩計算模型[24]。與SKF計算模型相比，該計算模型中考慮了材料彈性滯后造成的摩擦因素，以及鋼球與保持架、保持架與套圈之間的摩擦。

總的摩擦力矩為

M=Mrr+Msl+Mhys+Mcol+Mlub，

(8)

式中：Mhys為鋼球受載產生彈性滯后產生的摩擦力矩；Mcol為保持架產生的摩擦力矩，包含鋼球與保持架以及保持架與套圈之間的摩擦；Mlub為潤滑劑造成的摩擦力矩。

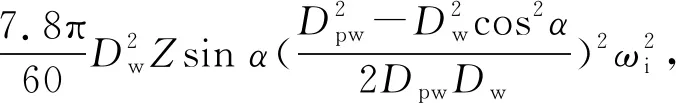
(9)

(10)

材料彈性滯后造成的摩擦力矩為

(11)

式中：Dw為鋼球直徑；Z為鋼球個數；ωi為內圈轉動的角速度；ri為內圈溝曲率半徑；re為外圈溝曲率半徑；βi為鋼球與外圈接觸的材料特性與幾何特征系數；βe為鋼球與外圈接觸的材料特性與幾何特征系數；μ為摩擦因數；α為接觸角；σi為第i個鋼球受載后發生Hertz接觸變形的最大值。

保持架產生的摩擦力矩Mcol為

Mcol=Mcolb+Mcole+Mcoli。

(12)

保持架產生的摩擦力矩包括鋼球與保持架的摩擦力矩Mcolb、保持架與外圈之間的摩擦力矩Mcole以及保持架與內圈之間的摩擦力矩Mcoli，即

(13)

式中：Decag為保持架外徑；Dicag為保持架內徑；ε為保持架的偏心率；Rca為保持架兜孔半徑。

由于拖拽損失、渦流和飛濺等導致的摩擦力矩Mdrag為

(14)

式中：f0為系數；v1為潤滑劑與鋼球相對速度。

2.3 理論計算模型的計算結果對比

以四點接觸球軸承JY204為例進行計算，該軸承套圈的幾何結構參數見表1。利用SKF修正模型計算其摩擦力矩為11. 6 mN·m；利用Florin T模型計算結果為52. 3 mN·m。

表1 軸承套圈結構參數

對比兩種計算模型，SKF計算模型中納入計算的軸承幾何尺寸參數只包括軸承的內、外徑與球組節圓直徑，而Florin T的計算模型中，除考慮這些參數之外，還考慮了鋼球直徑，鋼球個數，接觸角，套圈的溝曲率，保持架的內徑、外徑、兜孔半徑及其偏心率等參數。針對具體型號的摩擦力矩計算上，顯然Florin T的計算模型考慮得更為完善，后續的試驗數據也表明該模型的計算值更接近實測值。

Florin T的計算模型中，其他幾何參數的誤差對于計算值的影響較小，影響最為突出的因素為接觸角α。本計算中幾何參數的代入值均為設計值，沒有考慮加工誤差的影響。而四點接觸球軸承實際接觸角的影響因素很多，包括軸承的軸向游隙Ga、幾何尺寸參數(內溝道或外溝道的接觸點直徑D5或d5、內外溝道的溝底直徑D1或d1、內外溝道的溝曲率半徑re1與re2或ri1與ri2)、溝道形位公差(包括套圈接觸點位置的圓度Cir、對稱溝道中心與端面平行度Se與Si、外圈或內圈溝道接觸點與外圈或內圈表面間的厚度變動量Ke與Ki、兩對稱溝道相對于基準面厚度變動量Ker，溝道的輪廓度ΔCur)等，如圖2所示。這意味著實測值與考慮內部幾何結構參數的理論計算模型值仍將有較大差異。

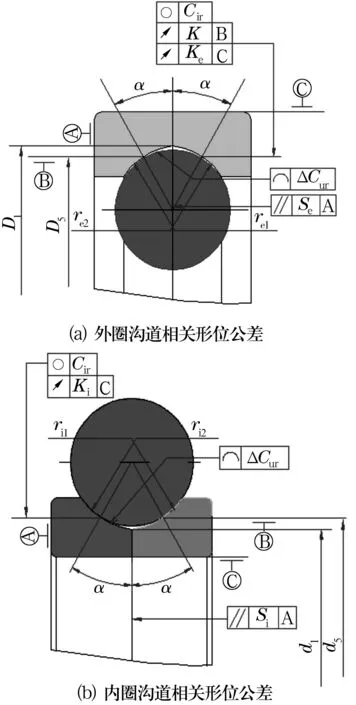
圖2 影響四點接觸球軸承實際接觸角的溝道尺寸與公差

在溝道的幾何參數中，溝道的接觸點直徑誤差直接影響游隙值的大小，對接觸角產生直接影響；溝道曲率半徑的誤差以及同一套圈的兩溝道之間曲率的一致性也將影響游隙值并最終影響接觸角。因而實際生產中應嚴格控制內溝道或外溝道的接觸點直徑D5或d5，以保證合套率、游隙值以及正確的接觸角。嚴格控制接觸點直徑還能消除部分由于溝曲率誤差造成的接觸角變化。

在形位公差參數中，Se(Si)，Ker或ΔCur可造成單一截面上實際接觸角與理論接觸角的差異；Cir或Ker可造成圓周面上的實際接觸角變化。

3 游隙對實際接觸角的影響

3.1 原始游隙的影響

軸承的游隙包括裝配游隙、安裝游隙以及工作游隙，軸承從裝配完成到使用過程中，若游隙發生變化，則其接觸角也將產生變化。由于軸承內部游隙的存在而造成的接觸角變化如圖3所示，圖3a為徑向游隙造成的實際接觸角變化，圖3b為軸向游隙造成的實際接觸角變化。假定外圈溝曲率系數為fe，內圈溝曲率系數為fi，軸承初始外圈上溝道曲率中心為Ceu，外圈下溝道曲率中心為Ced；內圈上溝道曲率中心為Ciu，內圈下溝道曲率中心為Cid；鋼球初始中心為O。則內圈上溝道與外圈下溝道溝心距為

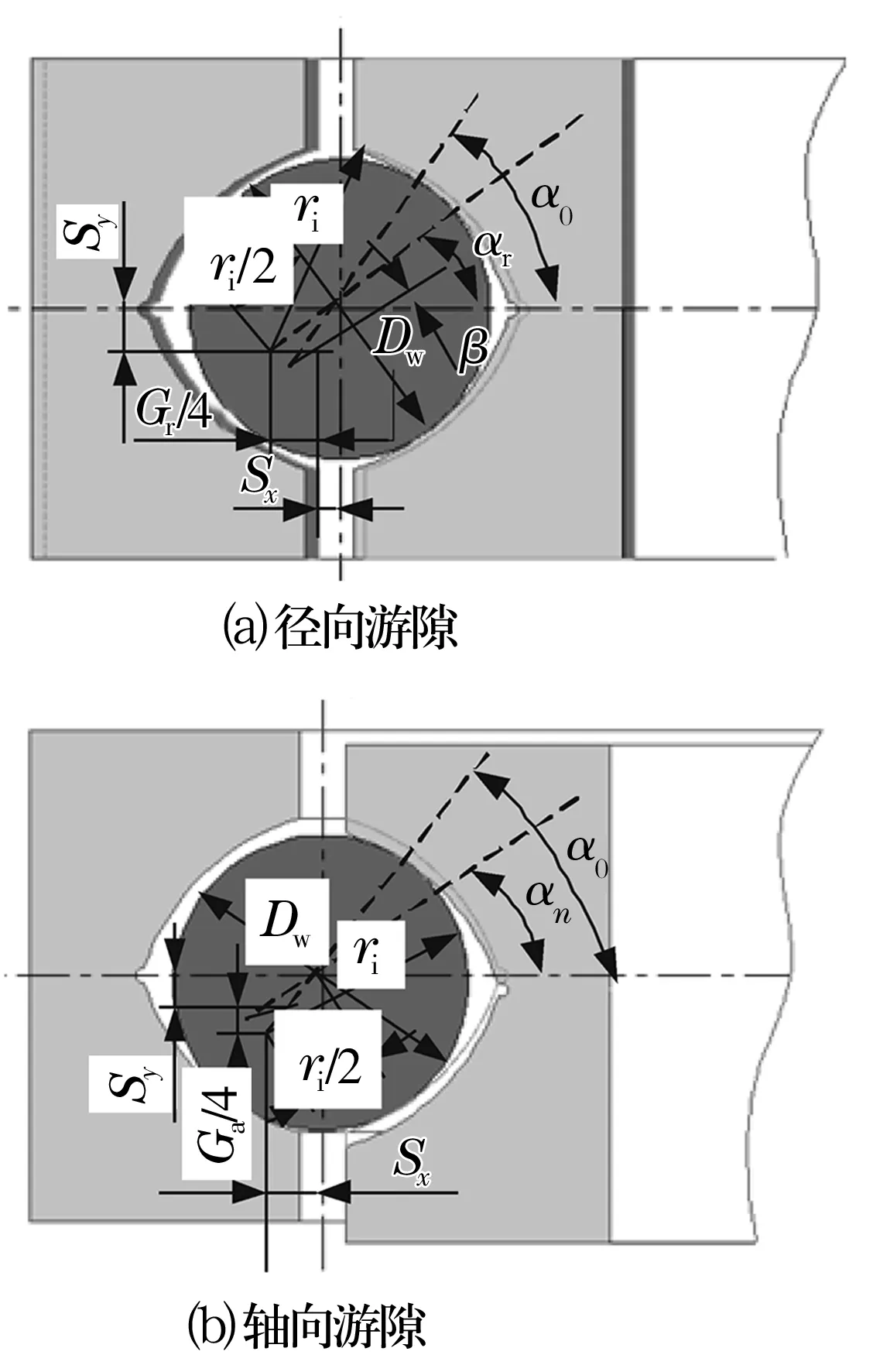
圖3 四點接觸球軸承游隙對接觸角的影響

A=(fi+fe-1)Dw，

(15)

設計接觸角α0為

(16)

徑向游隙為Gr，設計接觸角為α0，假設外圈固定，內圈移動，則沿徑向移動距離為Gr/4，則接觸角由α0變化為αr；軸向游隙為Ga，設計接觸角為α0，假設外圈固定，內圈移動，則沿軸向移動距離為Ga/4，則接觸角由α0變化為αn。

(17)

3.2 曲率變化的影響

目前四點接觸球軸承溝道終加工除部分采用數控硬車外，大量采用切入磨加工。采用切入磨法加工溝道時，溝道形狀靠砂輪修整出來的形狀保證，砂輪修整精度以及磨削過程中的砂輪磨耗對于溝道形狀有直接影響。

溝道曲率變化對實際接觸角的影響如圖4所示。圖4a為溝曲率增加使實際游隙增大，進而導致接觸角增大；圖4b為溝曲率減小使實際游隙減小，進而導致接觸角減小；圖4c與圖4d為溝道曲率不一致(偏溝)導致的接觸角變化。對于帶預緊的負游隙四點接觸球軸承，溝道曲率不一致會嚴重阻滯鋼球回轉，增加摩擦力矩。但對于游隙為正的四點接觸球軸承，其影響形式仍為游隙變化造成的接觸角變化。

圖4 溝曲率對接觸角的影響

為了更清晰地說明問題，圖4選取溝底徑作為溝曲率變化的基準位置，但實際生產中控制的是溝道接觸點尺寸，保證接觸點位置可適當消除由于溝曲率誤差導致的游隙與接觸角的變化。

4 溝道形狀對實際接觸角的影響

在加工精度的影響因素中，除幾何尺寸變化造成游隙變化進而影響接觸角外，形位公差造成的實際接觸角變化的波動性更為顯著，進而導致摩擦力矩的波動。由于砂輪形狀不恰當時形成的溝道形狀示意圖如圖5所示，圖5a為單一截面示意圖。由圖可知，單一截面上，Se(Si)，Ker和ΔCur的偏差都將影響到實際接觸角的大小，整個回轉面上，Cir或Ker導致軸承轉動時的實際接觸角變化。

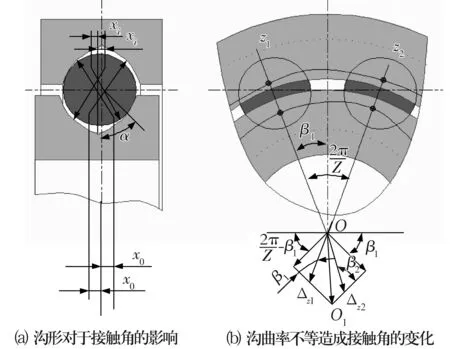
圖5 形位公差對四點接觸球軸承接觸角的影響

當要求軸向游隙時，對(17)式計算其全微分(為了表達更清晰，全微分時將內、外溝道溝曲率系數以溝道半徑與鋼球直徑的比值的形式表示)，則有

(18)

則在單一截面上由形位公差造成各尺寸公差反映到接觸角的變化上可以表示為

(19)

圖5b為鋼球從OZ1位置轉動到OZ2位置的過程中，由溝道的形位公差造成的鋼球位置、接觸角以及摩擦力矩的變化。由溝形變化產生的附加摩擦力矩為

(20)

式中：Δz1和Δz2為Z1與Z2方向上由溝形變化導致的位置變化量。

5 試驗

5.1 試驗方案

為研究溝道形狀對于摩擦力矩的影響關系，選取10套JY204四點接觸球軸承進行試驗。首先采用東京精密1600D輪廓儀測量軸承內、外圈的接觸角。指定輪廓儀的原因在于其他類型輪廓儀尚無法測量套圈的接觸角。需要指出的是：采用1600D測量零件實際接觸角的過程，是輪廓儀依據測量結果繪制出溝道實際輪廓后，利用儀器后臺程序將鋼球直徑的理論值與繪制出的溝道實際輪廓相切，從而得到零件的實際接觸角。裝配時鋼球的實際直徑值與理論值之間存在尺寸誤差，故該測量方法存在一定的原理誤差。但由于鋼球精度相對于溝道精度要高，所以該誤差影響可以忽略。

因為四點接觸球軸承裝配后鋼球與內、外圈溝道同時接觸，所以文獻[7]提出了桃形溝道接觸點測量方法，采用測長儀測量并換算成實際接觸角。但文獻[7]介紹的是特大型四點接觸球轉盤軸承的實際接觸角測量方法，而本試驗軸承尺寸較小，故測量精度很低。

使用德國Mahr 828PC測長儀測量，其分辨率為0.01 μm，精度為0.15+L/2 000 μm。測長儀的原測頭為尖頂，為了滿足試驗要求，在測長儀端部焊接試驗軸承裝用的鋼球，鋼球直徑3.968 8 mm，分規值-2 μm。使用測長儀測量接觸點位置到基準位置的距離并換算成實際接觸角。

最后將試驗套圈合套測試摩擦力矩，測試時不加載，水平放置，內圈固定，外圈旋轉，轉速為100 r/min。

5.2 結果分析

測試結果見表2。測量所得摩擦力矩值與兩種計算模型的計算結果差異都很大(SKF修正模型計算結果為11. 6 mN·m；接觸模型計算結果為52. 3 mN·m)，實測值遠遠大于計算模型的計算值。

對比輪廓儀與測長儀的測試結果，測長儀測量并換算的內、外圈接觸角數值處于輪廓儀測量的上、下溝道接觸角中間，這是由于空間限制，測長儀的測頭難以保證與上、下溝道同時接觸；另外，測長儀采用實際鋼球，鋼球尺寸誤差也影響到測試結果，但測試結果的分布狀態能說明測量的可靠性。

采用輪廓儀測試時可判斷同一內圈的曲率狀態，采用測長儀加裝配鋼球測量時，無法分別測量出上、下溝道的接觸角，而是上、下溝道接觸角的綜合反應。序號為1，2與5的測長儀換算接觸角接近，其摩擦力矩值也較為接近。因而可判斷出實際接觸角對于實際摩擦力矩的影響非常顯著。

6 結束語

目前較為先進的2種四點接觸球軸承摩擦力矩計算模型中，摩擦力矩計算值差異均較為突出，2種計算模型計算值的差異在于有無考慮軸承內部幾何結構參數。本例設計了專門試驗測試四點接觸球軸承摩擦力矩以研究內部結構參數對于摩擦力矩的影響。

實測的摩擦力矩值遠大于理論模型的計算值，分析認為溝道加工精度對于摩擦力矩的影響也非常突出。對比實際接觸角接近的試驗樣本，發現軸承摩擦力矩也較為接近。