基于ANSYS的雙曲面斜滾子軸承離合器應力分析

李蕾，孫東輝，畢超

(沈陽航空航天大學 機電工程學院，沈陽 110136)

雙曲面斜滾子軸承離合器是一種靠摩擦力傳遞力矩的新型離合器，與普通的離合器相比具有結構緊湊、承載能力高、楔緊可靠和壽命長等優點[1]，被應用于工業自動化、航天等領域，具有廣泛的應用前景。

雙曲面斜滾子軸承離合器內、外圈與滾子接觸的工作面是標準單葉雙曲回轉面等距曲面[2]，滾子與內、外滾道的三維曲線接觸問題屬于非線性接觸問題。由于接觸力的大小對離合器的總體性能有著重要影響，因此其接觸問題的研究顯得尤為重要。文中從雙曲面斜滾子軸承離合器工作原理入手，根據滾子與內、外圈接觸曲線方程，采用UG建立內、外圈單葉雙曲面等距曲面的三維模型，再導入ANSYS軟件，利用其接觸分析的強大功能，盡可能真實地模擬離合器工況進行接觸分析，以期達到對此種新型離合器的全三維應力分析，同時分析了離合器不同的結構參數對等效應力的影響。

1 工作原理

雙曲面斜滾子軸承離合器結構如圖1所示。它由內圈、外圈、滾子和保持架組成。滾子軸線系單葉雙曲回轉面上的一條直線，如圖2所示，內、外圈與滾子接觸的工作面是標準單葉雙曲回轉面等距曲面，滾子與內、外圈形成空間曲線接觸[3]。單葉雙曲回轉面是由一條直素線(即滾子軸線)繞內、外圈軸線旋轉而成[4]。滾子軸線同內、外圈軸線為空間異面直線，空間夾角為β，在雙曲面上截取一部分曲面作為保持架的形狀曲面，曲面的形狀參數用所截取曲面的軸向位置Zc表示。

圖1 雙曲面斜滾子軸承離合器結構

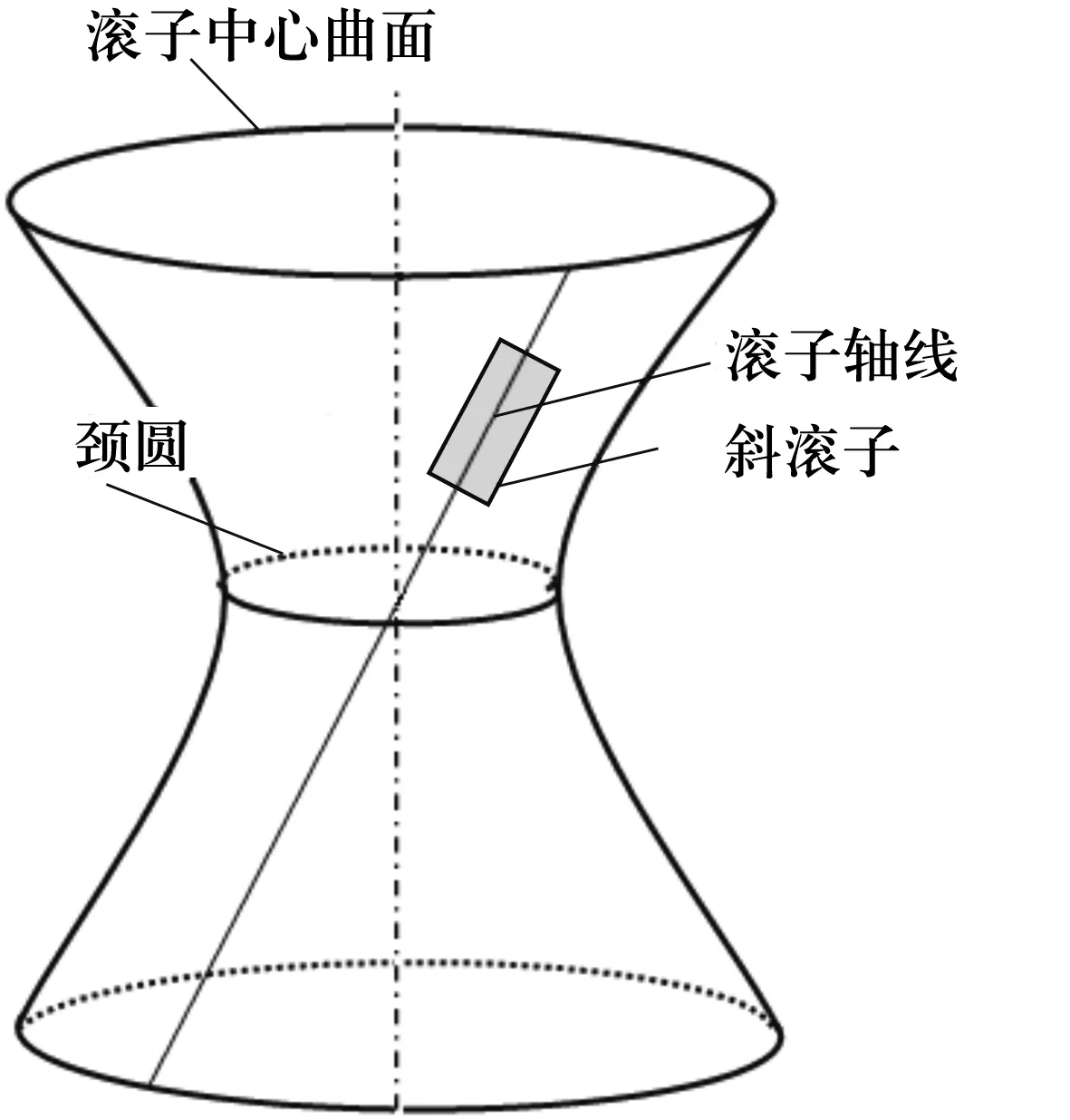
圖2 滾子軸線所在單葉雙曲面

雙曲面斜滾子軸承離合器可以是外圈做主動件，內圈做從動件；也可以是內圈做主動件，外圈做從動件。以下分析假設內圈為主動件，外圈為從動件。根據不同的設計參數，工作時分如下兩種工況。

(1)軸向載荷控制主動件與從動件的離合。離合器工作時，內圈逆時針(從上往下看)轉動的同時滾子既繞自身的軸線自轉又繞離合器的軸線公轉。當施加給內圈一軸向力時，滾子與滾道間將產生法向接觸力，由于滾子軸線與滾道軸線有一空間夾角β，所以滾子在做自轉和公轉的同時又必將沿著自身的軸線方向進行滑動，使接觸表面產生摩擦力，因而在這種滾滑摩擦狀態下產生的摩擦力矩使內圈傳遞轉矩帶動外圈轉動[5]。離合器的楔合或脫開類似于單向超越離合器的超越功能，依靠主、從動部分相對轉動速度的變化實現。當外圈轉速超越內圈轉速時，離合器脫開，內圈和外圈分別以各自的速度轉動；否則，離合器楔緊，內圈、外圈和滾子一起轉動。

(2)靠自鎖控制主動件與從動件的離合。與錐螺紋擰緊過程相似，它是以一定螺旋角排列的滾子替代錐螺紋的螺牙[1]，滾子在內、外圈滾道上呈右旋排列時，在一定的軸向預緊力下，當內圈在扭矩的作用下逆時針(從上往下看)轉動時，由于內、外圈與滾子3者中只有內圈可沿著軸線方向向上移動，致使內、外圈之間的法向間距減小，當滾子上壓力增大到一定程度而楔緊即產生自鎖，此時內、外圈與滾子可看成一體，并以相同的角速度轉動，僅通過滑動靜摩擦力的作用傳遞轉矩。與此相反，當內圈相對于外圈順時針方向轉動時，內圈沿軸向向下移動，內、外圈之間法向間距變大，滾子自由轉動，此時離合器脫開。若滾子在內、外圈滾道中呈左旋排列時，則與上述運動情況相反，內圈順時針方向轉動時離合器楔緊，逆時針方向轉動時脫開。文中選取第2種工況，對離合器自鎖狀態下的接觸應力進行數值模擬分析。

2 滾子與內、外圈工作面接觸分析

2.1 接觸對類型分析

從材料屈服的角度看，滾子與滾道曲面接觸形成的最大Von Mises等效應力限制了斜滾子離合器所能傳遞的極限力矩，而斜滾子離合器只有在楔緊狀態下方能傳遞扭矩。研究離合器的接觸應力問題，即對楔緊過程中滾子與內、外圈滾道間接觸面區域的接觸應力及整體Von Mises等效應力進行分析。在該離合器中，由于滾子與滾道材料的硬度相近，兩個接觸體都是變形體(假設剛度相同)，故可將問題歸結為柔體與柔體的面面接觸問題。

2.2 有限元模型的建立及簡化

在圖1所示OXYZ坐標系下，滾子與內、外圈接觸的三維曲線方程為[6]

式中：l為滾子的長度；r為滾子半徑；R為滾子中心雙曲面頸圓半徑；下標i和e分別表示滾子與內、外圈的接觸曲線。

根據接觸曲線方程，用UG中的表達式功能建立內、外接觸曲線，分別將內、外接觸曲線繞離合器的軸線旋轉一周即形成內、外圈的工作曲面。結合所選取的計算模型參數：滾子半徑r=3 mm，滾子長度l=20 mm，滾子個數Z=12，內圈孔直徑d=45 mm，外圈直徑D=96 mm，滾子軸線與內、外圈滾道軸線之間夾角β=30°，滾子中心雙曲面頸圓半徑R=33 mm，滾道曲面的軸向位置Zc=17.5 mm。利用UG強大的曲線曲面造型功能建立三維模型，如圖3所示，模型中忽略倒角和滾子的修形。采用parasolid格式，將其導入ANSYS中。

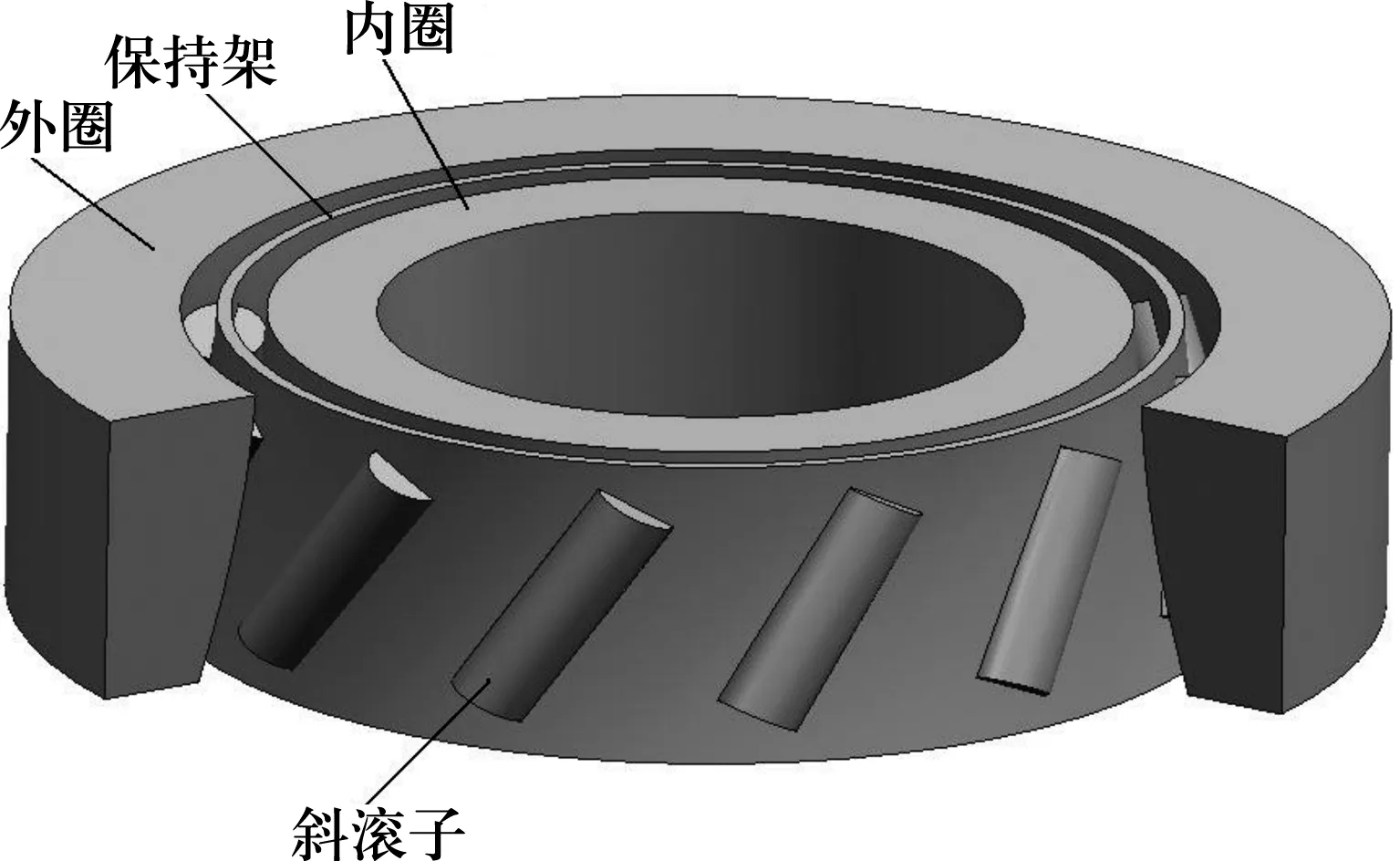
圖3 雙曲面斜滾子軸承離合器實體模型

考慮到離合器結構的對稱性和受力特點，為簡化計算，進行軸對稱處理，截取整圈的1/12進行分析。滾子和內、外圈材料均選用軸承鋼G20Cr2Ni4，彈性模量為206 GPa，泊松比為0.3。計算單元選擇Solid 186(3維20節點六面體等參實體單元)，整體有限元模型網格劃分方式采用智能網格(4級SmartSize)，對滾子與內、外圈接觸區域進行局部細化，細化網格尺寸小于接觸橢圓短半軸尺寸的50%為宜[7]，劃分后共有100 427個單元，132 095個節點。圖4為簡化后的網格劃分模型。接觸單元用Contact 3D Target 170模擬內、外圈滾道表面，用Contact 8nd surf 174模擬圓柱滾子的外表面。分別定義滾子與內、外圈之間的接觸對，摩擦因數(鋼與鋼)取0.1，設置法向接觸剛度因子FKN=0.5，切向接觸剛度FKT=1.0，最大滲透容差FTOLN=0.1，初始閉合因子ICON=0.01，選取非對稱剛度矩陣Unsymmetric。圖5所示為定義的接觸對圖。

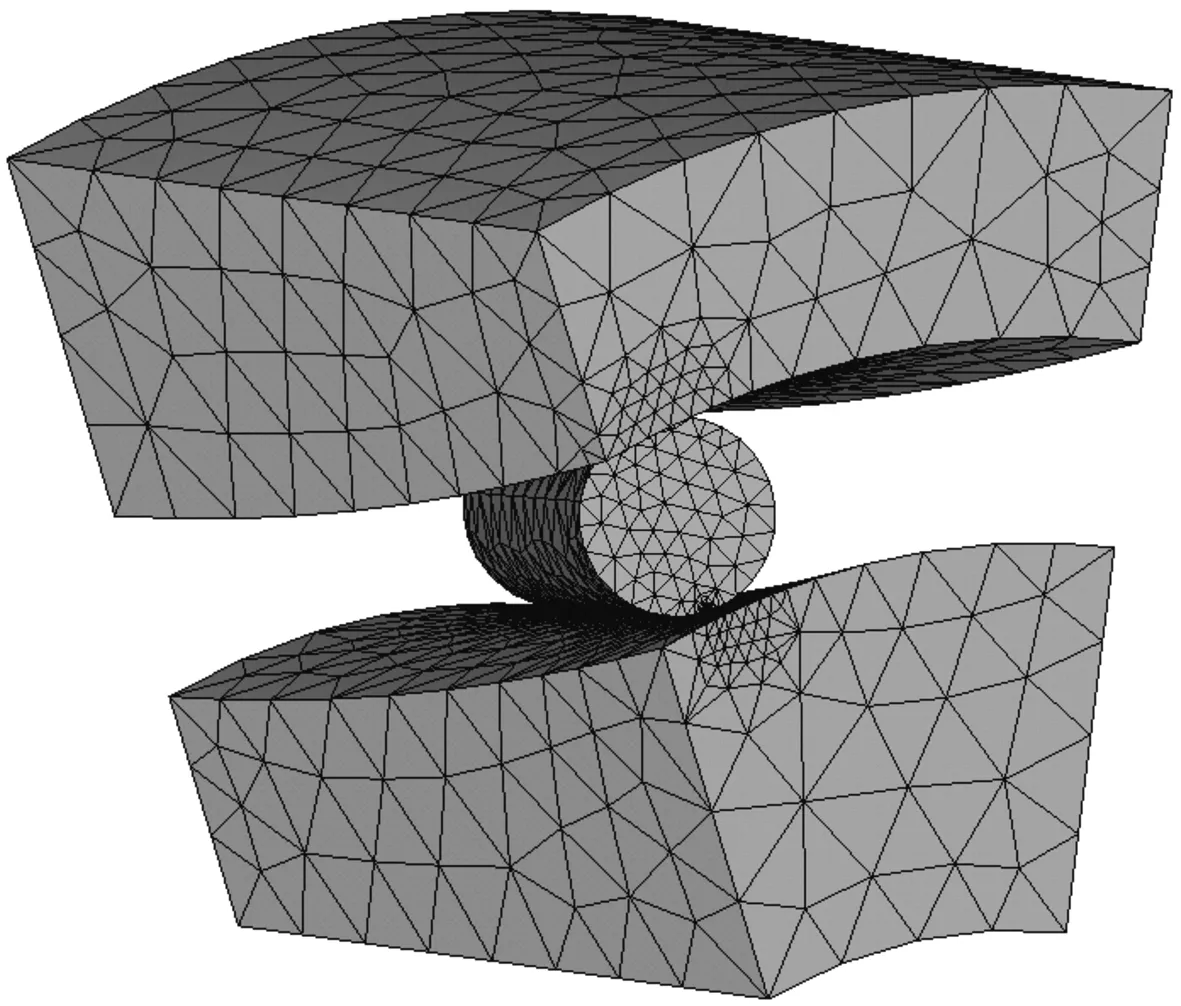
圖4 網格劃分模型

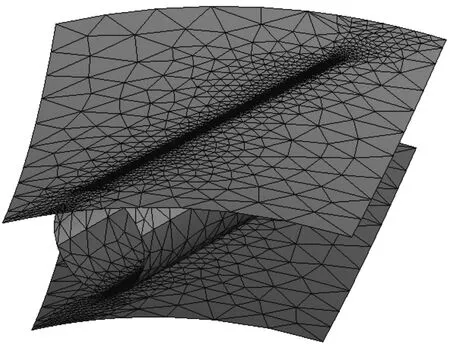
圖5 接觸對

2.3 約束條件、施加載荷與求解

保持架的模擬可簡化為：把滾子外表面節點轉換到以滾子中心為原點創建的局部柱坐標系下，并約束這些節點的切向(UY)位移。外圈側面約束其UZ向的位移，耦合內圈內表面上所有節點的徑向(UX)及周向(UY)的自由度，使得在軸向載荷下能保持內圈內表面的剛性。為了定性地分析結構參數對等效應力的影響規律，在進行ANSYS分析時，考慮到調整模型結構參數可能出現最大等效應力大于材料許用極限應力的情況，故在外圈外表面施加數值較小的均布面載荷P(P=500 Pa)。同時內圈施加軸向位移UZ(UZ=8 μm)，截面處施加對稱自由度約束。約束條件及施加的載荷如圖6所示。

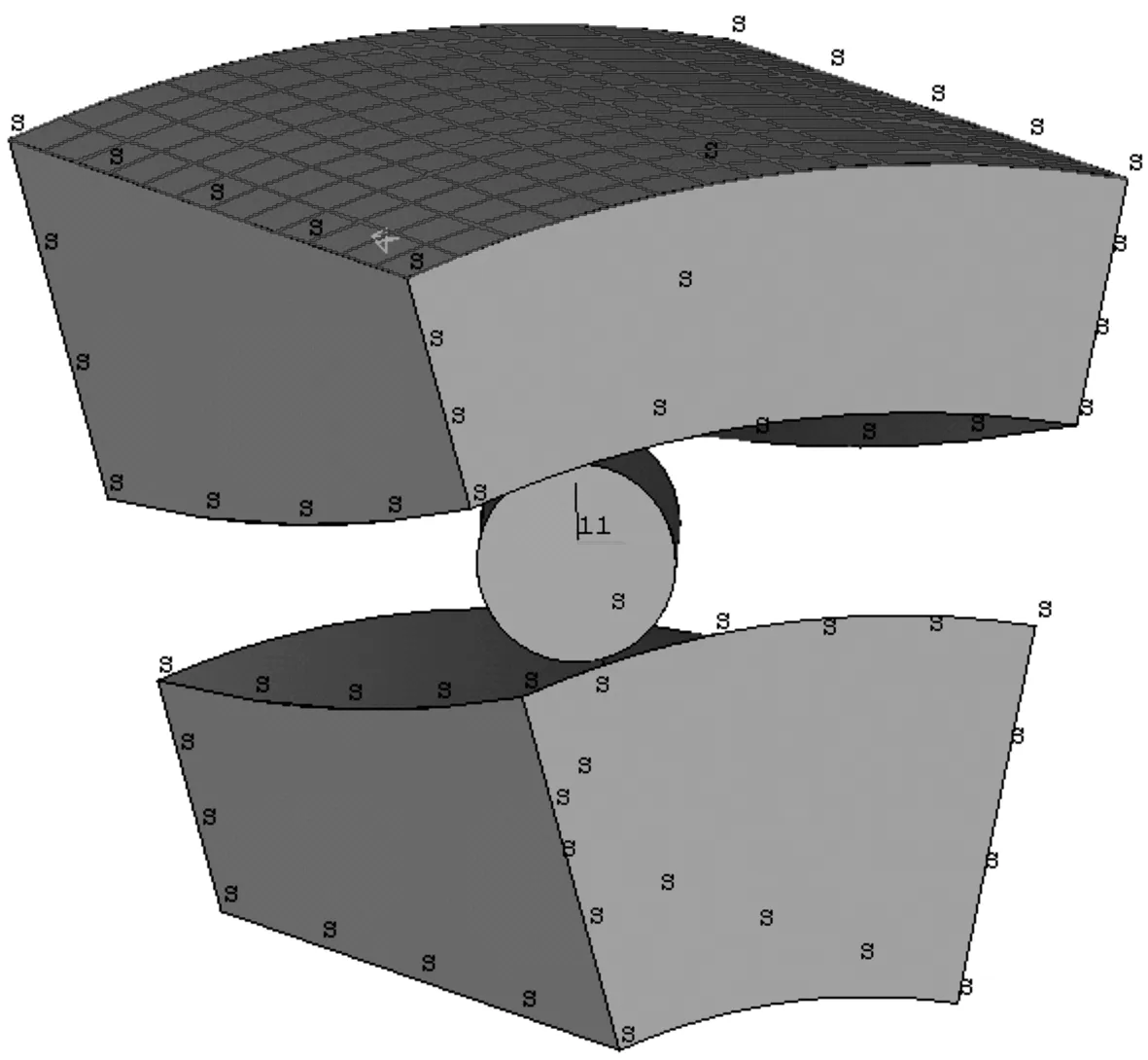
圖6 約束與加載

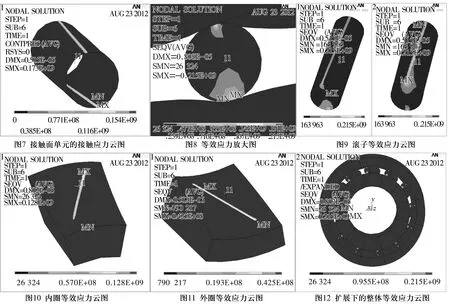
打開自動時間步長，設定子載荷步數為 10，最大子步數為 100，最小子步數為 1，打開預測器使用線性搜索來加強非線性迭代的收斂，然后進行非線性分析，計算結果收斂。由分析結果可以看出，在外載荷作用下，接觸面單元的接觸應力分布如圖7所示，最大接觸應力值為173 MPa。

在相同工況條件下，采用Hertz理論[8]簡化力學模型得出最大接觸應力值為204.4MPa。該結果表明，有限元數值計算與理論分析結果存在的誤差在工程容許的范圍內，且數值計算方法更為方便有效。圖8為Von Mises等效應力放大圖；圖9為滾子與內、外圈接觸時滾子的Von Mises等效應力云圖；圖10、圖11分別為內、外圈的Von Mises等效應力云圖；圖12為擴展下的整體等效應力云圖，可以方便觀察整體模型的應力狀態。

3 結構參數對Von Mises等效應力的影響

結構參數β，r，l，Zc，R和Z的取值直接影響離合器所受應力的大小、承載能力及整體結構尺寸，選擇合理的結構參數對提高離合器的使用性能和延長其使用壽命具有重要意義。

在相同模型和工況下，分析各結構參數對離合器Von Mises等效應力的影響。

當r=3 mm，l=20 mm，Zc=17.5 mm，R=33 mm，Z=12時，不同β角對應的最大等效應力如圖13所示。由圖可知，最大等效應力隨β的增大而增大。

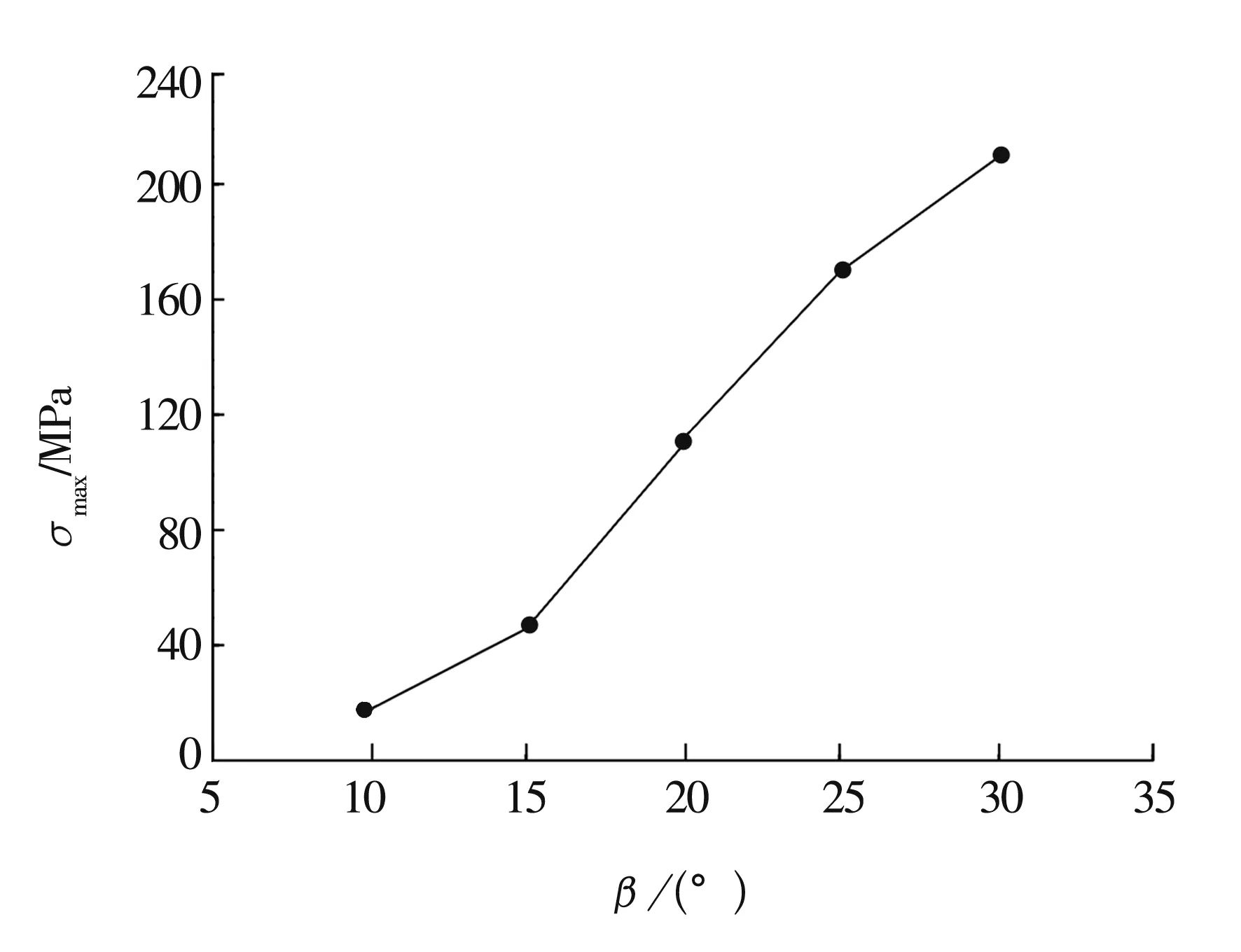
圖13 最大等效應力隨β的變化曲線

當β=30°，l=20 mm，Zc=17.5 mm，R=33 mm，Z=12時，不同的r對應的最大等效應力如圖14所示。由圖可知，最大等效應力隨滾子半徑r的增大而減小。

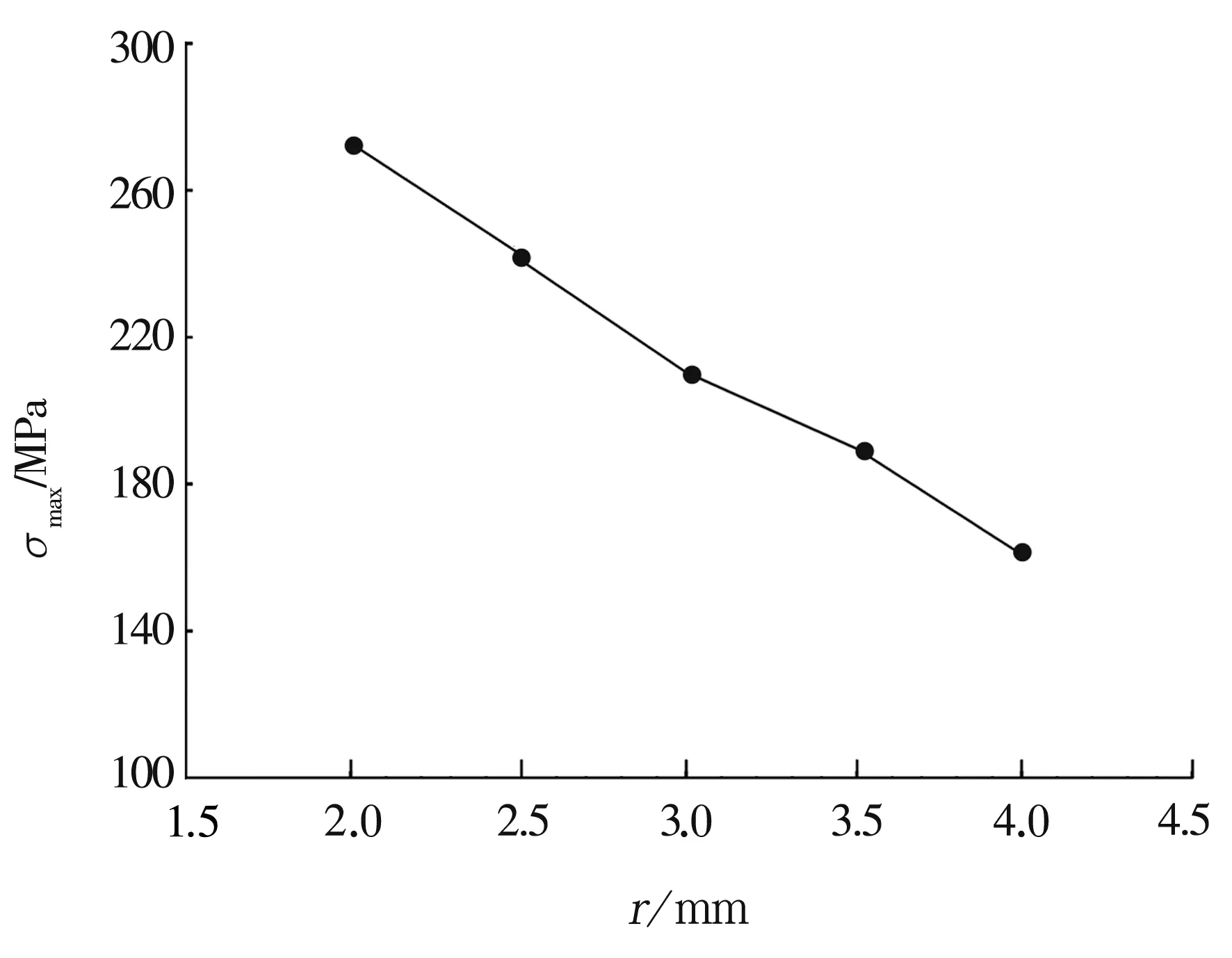
圖14 最大等效應力隨r的變化曲線

當β=30°，r=3 mm，Zc=17.5 mm，R=33 mm，Z=12時，不同的l對應的最大等效應力如圖15所示。由圖可知，最大等效應力隨滾子長度l的增加而減小。

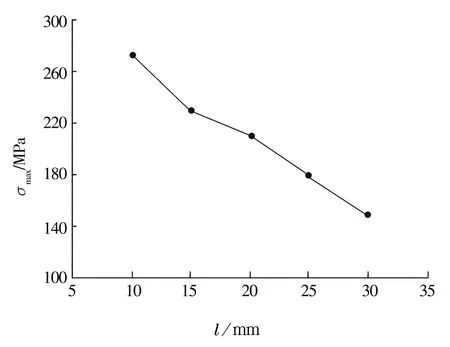
圖15 最大等效應力隨l的變化曲線

當β=30°，r=3 mm，l=20 mm，R=33 mm，Z=12時，不同的Zc對應的最大等效應力如圖16所示。由圖可知，最大等效應力隨軸向位置尺寸Zc的增大而增大。

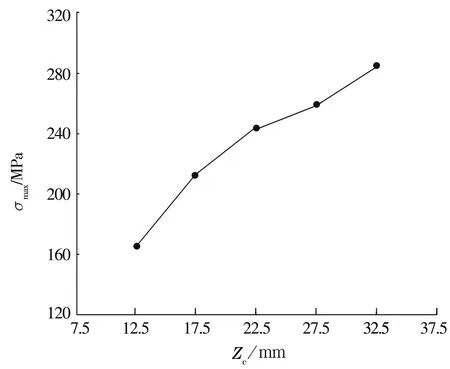
圖16 最大等效應力隨Zc的變化曲線

當β=30°，r=3 mm，l=20 mm，Zc=17.5 mm，Z=12時，不同的R對應的最大等效應力如圖17所示。由圖可知，最大等效應力隨R的增大而減小。

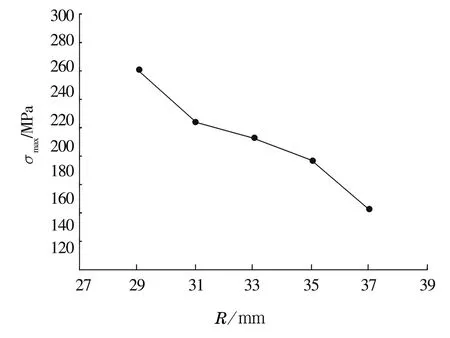
圖17 最大等效應力隨R的變化曲線

當β=10°，r=3 mm，l=20 mm，Zc=17.5 mm，R=33 mm時，不同的Z對應的最大等效應力如圖18所示。由圖可知，最大等效應力隨滾子個數Z的增加而減小。

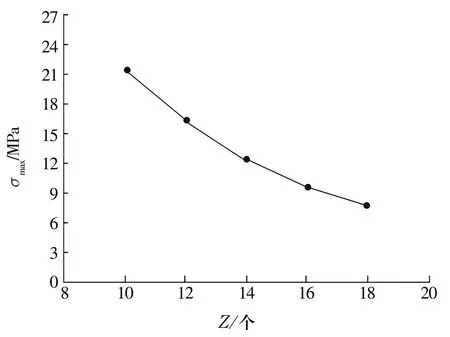
圖18 最大等效應力隨Z的變化曲線

4 結束語

(1)根據滾子與內、外圈接觸的曲線方程，采用UG建立全三維接觸模型，導入ANSYS對雙曲面斜滾子軸承離合器的接觸問題進行分析是一種行之有效的分析方法，可為產品結構的數字化設計提供較為實用的方法。

(2)滾子與內、外圈間接觸的最大等效應力隨β和Zc增大而增大；隨r，R,l和Z的增大而減小。

(3)在離合器設計時，應綜合考慮離合器的強度、離合性能和傳動要求等，以降低最大Von Mises等效應力，提高離合器的使用性能，延長其使用壽命。