小波SVM核函數法在滾動軸承故障診斷中的應用

高朋飛, 許同樂，侯蒙蒙，郎學政，李磊

(1.山東理工大學 機械工程學院，山東 淄博 255049；2.山東信遠集團有限公司，山東 萊陽 265200)

故障軸承的振動信號包含了故障特征信息，而且便于采集，因此振動信號分析成為故障診斷的有效手段之一[1-3]。小波分析不僅能對振動信號進行降噪處理，還能對信號進行進一步分解，提取不同頻段的故障特征，在信號處理領域得到了廣泛應用。支持向量機(Support Vector Machine，SVM)是一種基于統計學理論的模式識別方法，其克服了神經網絡結構選擇困難、容易陷入局部極小值等問題，并能很好地解決小樣本學習問題，已應用于許多領域[4-7]。

在此，提出了一種基于小波分析的SVM滾動軸承故障診斷方法，通過小波分析提取軸承的尺度能量譜,建立故障特征向量集，然后將其作為SVM的訓練樣本，并用改進的SVM核函數進行訓練，獲得故障分類模型，最后用該分類模型對未知故障信號進行預測分類。

1 基于小波分析的故障特征提取

采用小波閾值方法進行降噪，對降噪后的信號進行小波變換，可以得到信號的故障特征。設f(t)為有限能量函數，即f(t)∈L2(R)，則該函數的小波變換定義為

(1)

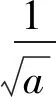
根據能量守恒可得

(2)

式中：Cψ為小波的容許條件；ω為頻率。

則f(t)在尺度a上的能量為

(3)

E(a)稱為尺度-小波能量譜，它反映了信號能量隨尺度的變化情況。

為了更好的分析和表征信號的能量特征，采用各個頻段能量在總能量Esum中所占的比例A(i)作為故障特征向量。選取所需要的頻率段信號，提取其尺度-小波能量譜并計算該能量大小，記為Ei，則

(4)

2 SVM故障分類器設計

2.1 支持向量機原理

支持向量機方法建立在統計學習理論的VC維理論和結構風險最小原理基礎上，它根據有限的樣本信息在模型的復雜性與學習能力之間尋求最佳折中，使結構風險最小，即同時最小化經驗風險和VC維的界，以獲得最好的泛化能力[7-9]。

以二分類為例，給定訓練數據樣本集：(xi,yi),i=1,2,…,n；x∈Rd,y∈{+1,-1}。其中n為訓練樣本數，d為每個訓練樣本向量的維數，y為分類標號。如果該樣本能被一個超平面線性分開，則該分類超平面的方程為wx+b=0，其中w為權系數向量，b為分類閾值。需要找到最優超平面，使訓練集中的所有樣本均能被該超平面正確分開，而且支持向量與超平面之間的距離最大[9]。

在線性可分的情況下，求最優分類面可轉化為在滿足yi(wxi+b)≥1的條件下求w2/2的最小值問題。此問題可以通過求解Lagrange函數得到解決，進而得到最優分類函數為

(5)

式中：αi為Lagrange乘子。根據f(x)的值就可以判斷x所屬的分類。

對于非線性分類，可以使用一個非線性映射Φ把數據樣本從原空間Rd映射到一個高維特征空間Ω，再在Ω中求最優分類面。根據泛函有關理論，只要一種核函數K(xi,xj)滿足Mercy條件，它就可以對應某一變換空間的內積，這樣在高維空間實際上只需進行內積運算，而這種內積運算是可以用原空間中的函數實現的，無需知道變換Φ(x)的具體形式。此時，最優分類面的形式為

(6)

在機械設備故障診斷中，簡單的二分類顯然不能滿足工程實際要求，因此需要支持向量機的多分類模型，可以分別用多個二分類器進行訓練，得到多分類模型。

2.2 新核函數

一個好的核函數不僅能夠解決樣本低維線性不可分的問題，還能在一定程度上優化SVM訓練算法，縮短樣本訓練時間。因此，選擇合適的核函數是建立最優SVM模型的關鍵，直接影響模型的訓練精度、訓練速率和泛化能力[10]。目前，如何選取核函數還缺乏統一的理論指導，比較常用的核函數有4種：

(1)線性核函數，K(x,y)=xy，就是線性支持向量機采用的核函數。其僅適用于簡單的線性分類問題，無法解決大多數復雜的非線性分類問題。

(2)多項式核函數，K(x,y)=(xy+1)d，其中d=1，2，3…，為多項式的階數。在特征空間維數很高時，該核函數的d值很大，將使計算量大大增加。

(3)Sigmoid核函數，K(x,y)=tanh[v(xy)+c]，其中v,c分別為比例、偏移參數。其必須在某些特定條件下才滿足對稱、半正定的核函數條件，在應用上受到一定的限制。

(4)徑向基核函數，K(x,y)=exp{-x-y2/2σ2}，其中σ為函數的寬度參數。徑向基核函數最為常用，但σ的不同取值直接影響向量機的支持向量個數和訓練得到的超球面的形狀，容易產生超球面空間不穩定和泛化能力降低等問題，而且對于不同的訓練樣本，問題的出現形式也不同，其應用也存在一定的局限性。

為此，提出一種新的核函數

z=max‖x-y‖。

(7)

新核函數滿足Mercy條件且結構形式簡單，當訓練樣本維數較多時，計算量也較小。而且核參數z不需賦值，而是取決于數據樣本，可以根據樣本輸入自動調整，實現自適應訓練，解決了徑向基核函數中σ的選擇問題，適用于大部分復雜非線性分類問題。

為驗證新核函數的優越性，對不同核函數的SVM模型進行了仿真分析。由仿真結果可知，與其他核函數相比，新核函數顯著提高了訓練精度，預測分類準確率也較高，說明該模型有較好的學習能力和泛化能力。

2.3 小波尺度-能量譜SVM故障診斷模型

小波尺度-能量譜SVM故障診斷的原理圖如圖1所示，首先，對獲得的故障振動信號進行預處理，應用小波分析進行降噪，對降噪后的信號進行小波分解與重構，提取故障信號的小波-尺度能量譜，并建立故障特征向量集；然后，以此特征向量集作為SVM訓練的輸入樣本，應用提出的新SVM核函數對故障特征進行訓練，通過調節參數使準確率符合要求，繼而建立SVM故障診斷模型；最后，將未知樣本數據輸入診斷模型，再進行預測分類并輸出相應的診斷結果，從而實現滾動軸承的故障診斷。

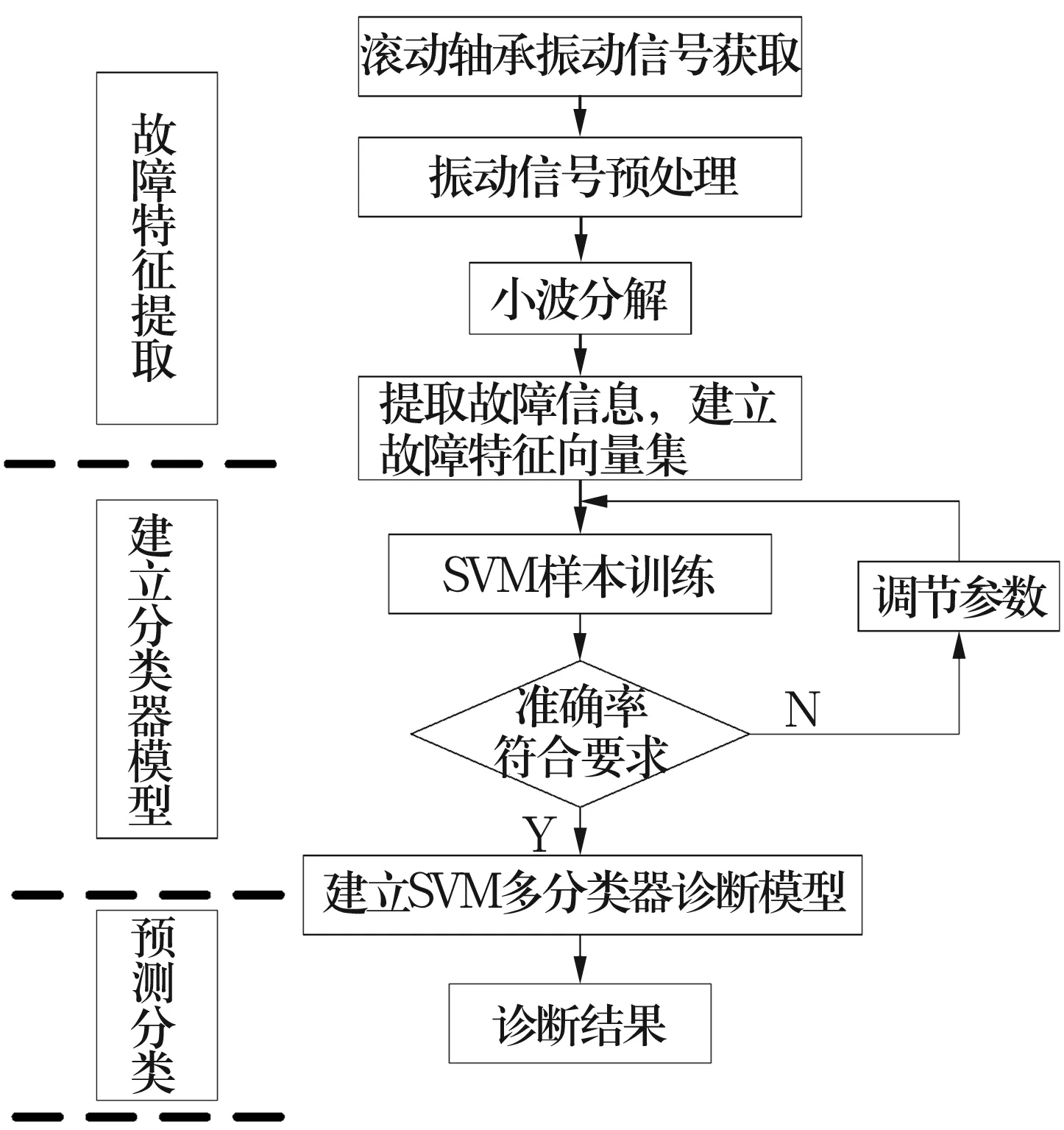
圖1 小波尺度能量譜SVM故障診斷原理

3 試驗驗證

3.1 信號提取

試驗軸承型號為6004zz，內徑為20 mm，外徑為42 mm，寬度為12 mm，鋼球個數為9，鋼球直徑為6.35 mm。外圈固定，內圈旋轉。故障模式為單一故障，其中內圈與外圈故障為裂紋，分布在溝道處，長約1 mm；鋼球故障是在其表面切掉了一小部分，不影響正常滾動。

在試驗臺軸承基座的水平方向和垂直方向上布置2個振動測試點，加速度傳感器安裝在電動機驅動端，測量軸承振動加速度信號。為獲取軸承故障的相關數據，試驗臺上分別進行了正常及3種典型故障的模擬試驗。試驗數據均進行多次采集，試驗采樣頻率為12 kHz，軸承轉速為1 750 r/min。

軸承振動信號的時域圖如圖2所示，可以看出，故障信息非常不明顯，基本上都被噪聲淹沒，無法識別是否存在故障以及故障類型。如果對其直接進行頻譜分析，診斷效果不是很好。

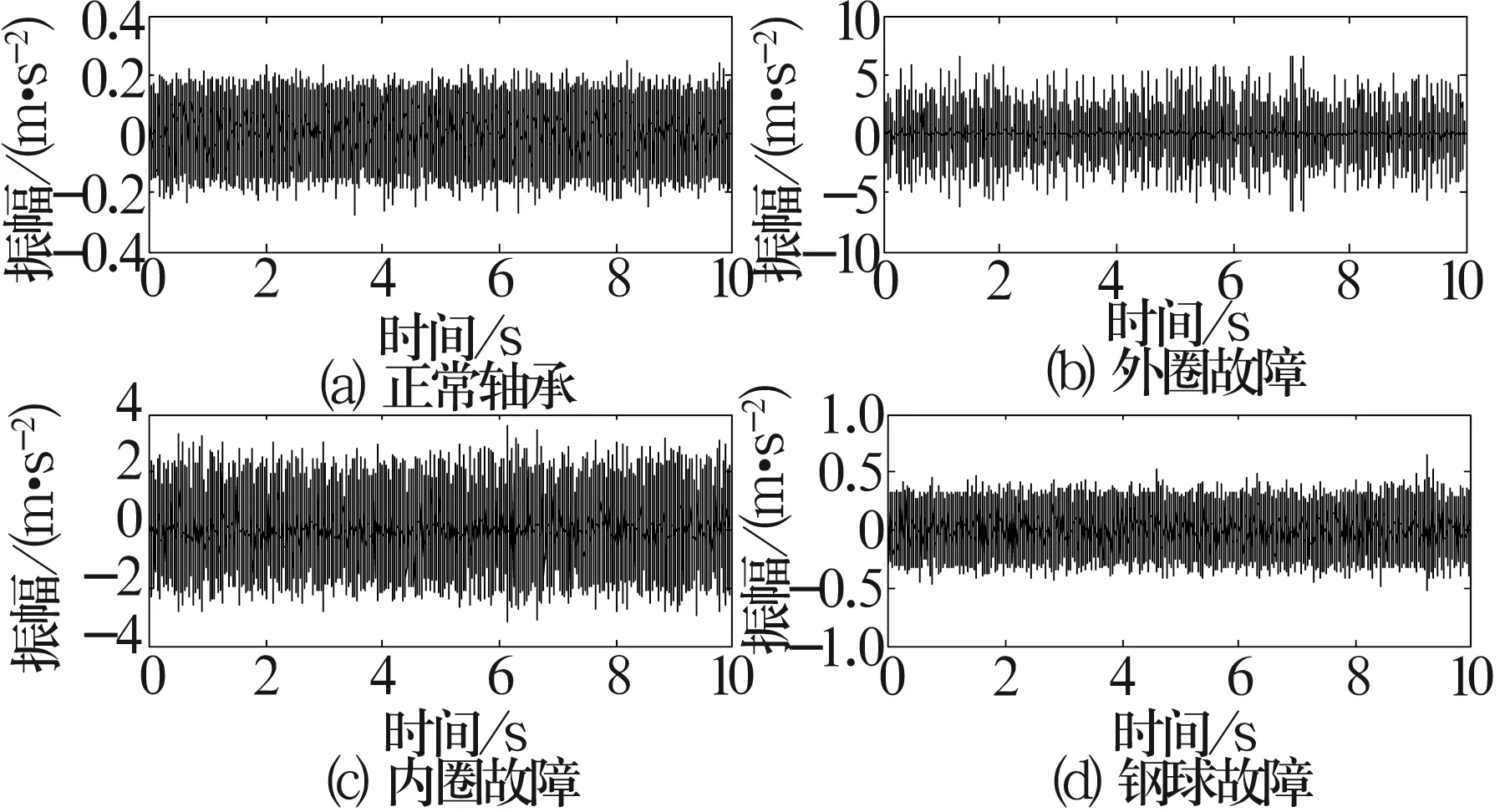
圖2 不同故障類型軸承的振動信號

對振動信號進行預處理，應用小波閾值方法對振動信號降噪，去除大部分噪聲；然后采用db4小波基對信號做4層小波包分解，得到表征故障特征的尺度能量譜，也就是信號的能量系數比，如圖3所示。

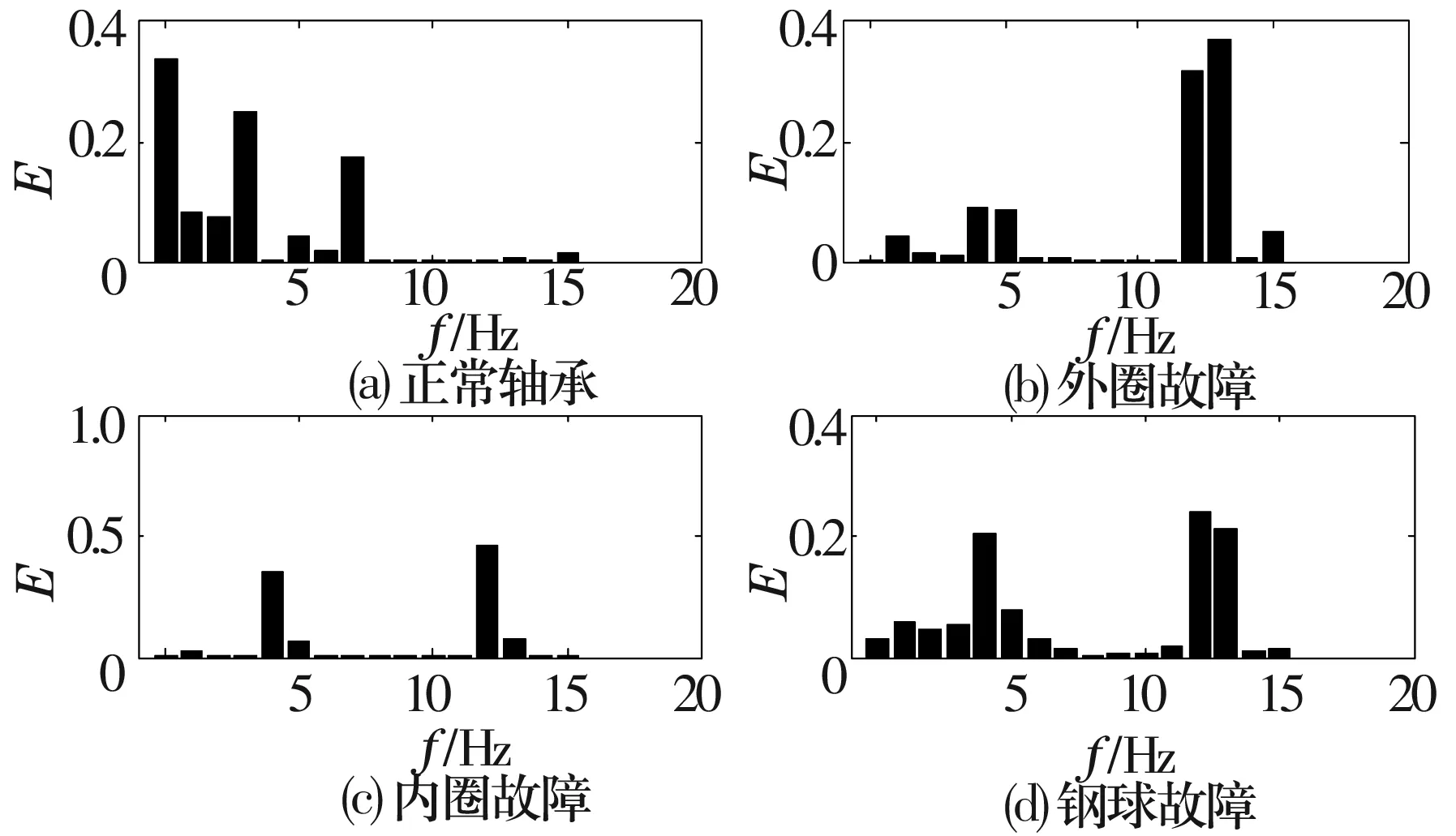
圖3 不同故障類型軸承的故障特征對比

由圖3可知，不同故障的能量特征譜有明顯的差別。正常軸承的能量大多分布在低頻段，高頻段能量很小；外圈故障軸承由于受到振動沖擊，在高頻段有很高的能量，低頻段也有小部分能量；內圈故障軸承的高、低頻段各有一部分能量，但能量分布比較集中；鋼球故障軸承在高頻段能量分布較集中，低頻段能量分布則趨于分散；因此，提取軸承各個頻段的能量，將其進行歸一化等處理后作為故障特征向量集，然后應用SVM方法可以對故障特征進行預測和分類。

3.2 數據處理

為避免樣本數據差距過大對分類預測的影響，必須對樣本數據進行歸一化預處理，將其線性調整到[-1,+1]區間。

隨機選取參數是利用程序隨機選取懲罰參數和核參數，當有多組懲罰參數對應于最高分類準確率時，選取最小的一組作為最佳懲罰參數，因為過高的懲罰參數會導致過學習狀態的發生，即訓練集分類準確率很高而測試集分類準確率很低，也就是說分類器的泛化能力降低。

為了得到比較理想的分類準確率，采用交叉驗證(Cross Validation，CV)的方法對懲罰參數和核函數參數進行尋優，選取準確率最高的一組作為模型的參數。交叉驗證即將原始數據分為訓練集和驗證集2組數據，依次使用訓練集和驗證集對分類器進行訓練和驗證，以分類準確率作為分類器的性能指標。

從軸承故障信號中選取320組數據。其中160組數據(每種故障類型選取40組)作為故障的訓練樣本，剩余160組數據作為測試樣本。為驗證新核函數分類模型的學習能力和泛化能力，分別應用新核函數和徑向基核函數進行訓練,然后再用測試樣本進行檢驗。結果見表1。

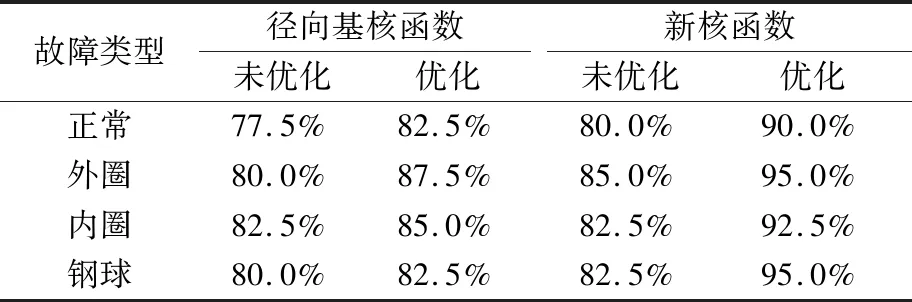
表1 不同核函數SVM診斷模型的分類準確率

從表1可知，對于徑向基核函數SVM模型，未經優化訓練的分類模型由于發生了過學習和欠學習，預測準確率不高，為80%左右；而采用CV進行參數優化后，準確率稍有提高，但仍不足以用于模式識別與故障診斷。

而新核函數在樣本維數較多時，有很好的空間穩定性。表中未優化參數時，準確率同樣不高；而優化后的參數訓練模型的分類準確率有顯著提高，160個樣本中僅有11個樣本被誤識別。由此可見，新核函數訓練得到的模型不僅有很好的學習能力，也具有較好的容錯能力和泛化能力，在故障分類方面比徑向基核函數更優越。

4 結束語

利用提出的新SVM核函數進行訓練，并采用交叉驗證的方法對訓練參數進行尋優，有效的克服了過學習和欠學習的發生，并獲得了更高的準確率，更好的學習能力和泛化能力，能夠有效的對軸承故障進行分類。但是對于工業環境中的故障軸承而言，故障振動信號本身具有復雜性，該方法能否準確診斷還需作進一步研究。