懸臂梁智能結構主共振響應的最優化控制

劉燦昌 裘進浩 孫慧玉 季宏麗 劉 露

1.南京航空航天大學機械結構力學及控制國家重點實驗室，南京，210016

2.山東理工大學，淄博，255049

0 引言

機械柔性結構在工程領域得到廣泛應用，如航天飛機和大型空間站中的柔性機械臂、太陽能帆板以及衛星天線等。隨著機械結構不斷向大型化、高速化和柔性化方向發展，對結構的精度、可靠性和穩定性的要求也越來越高，非線性因素對結構設計和控制的影響也越來越突出，因而柔性結構的動力學振動與控制問題的研究顯得日益重要。國內外很多學者使用理論分析和實驗方法對機械系統的非線性動力學特性進行了研究［1－3］。李韶華等［4］利用平均法研究了單自由度多頻激勵非線性汽車懸架系統的主共振和系統參數對汽車主共振控制的影響。馮霏等［5］研究了主共振、超諧波共振、次諧波共振以及內組合共振條件下的非線性懸架系統在非線性參數不同時的幅頻響應。丁虎等［6］運用微分求積法數值研究了不同邊界條件下軸向運動黏彈性梁受到簡諧外激勵的橫向受迫振動穩態響應問題。趙艷影等［7］研究了時滯非線性動力吸振器對承受外激勵的主系統減振的作用規律，通過調節反饋增益系數和時滯來控制主系統的振動。

本文提出一種結構體非線性振動的最優化控制方法。利用懸臂梁主共振振動實驗實測數據，用最優化方法計算得到速度和位移控制參數，設計最優化控制器，搭建實驗控制電路，將粘貼在梁上的壓電傳感器產生的電壓信號輸入到控制系統，控制系統將輸入的信號進行放大處理后輸給壓電驅動器，由壓電驅動器對梁的振動進行控制。

1 主共振響應的減振控制

懸臂梁模型假設為Euler－Bernoulli梁，當激勵力頻率接近于梁某階振動模態的固有頻率時，系統會發生主共振響應，這時主共振梁可以簡化為單自由度振動系統，其振動的動力學方程可以寫為［8－10］

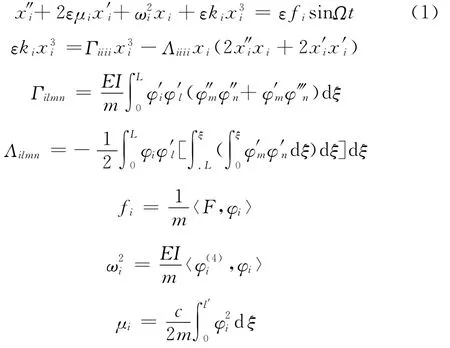
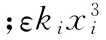
引入正小參數ε和含有位移及速度反饋控制器，非線性振動系統的動力學方程可寫為

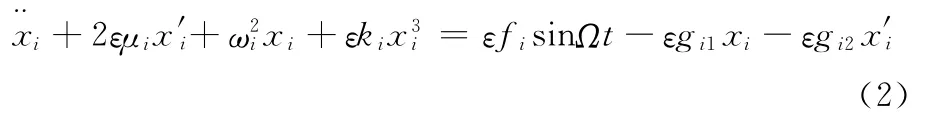
式中，gi1為位移反饋系數；gi2為速度反饋系數。

為計算簡便，作如下變換，令

則式（2）成為

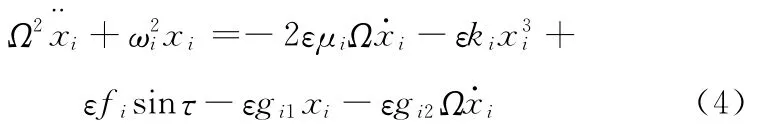
當柔性體結構為弱幾何非線性時，小阻尼和小激勵作用情況下，通常將結構的振動近似看作弱非線性振動［9-11］。對懸臂梁柔性結構的主共振分析，大部分文獻采用弱非線性的處理方法［11-14］。本文研究的懸臂梁為一柔性結構，基礎激勵較小，其振動可以近似視為弱非線性振動，可以采用攝動法分析其振動控制行為，將式（4）的響應解和激勵頻率寫為冪級數形式：

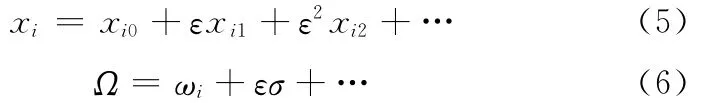
其中σ為調諧參數。將式（5）和（6）代入式（4），令方程兩邊ε的同次冪的系數和為零，得到

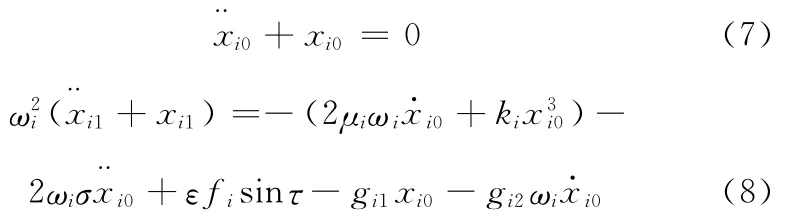
式（7）的解為

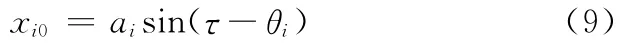
式中，ai、θi分別為振動幅值和相位。

將式（9）代入式（8）得到

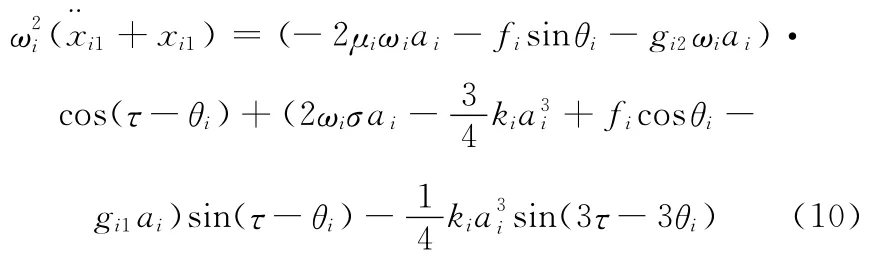
消除式（10）中的久期項，得到

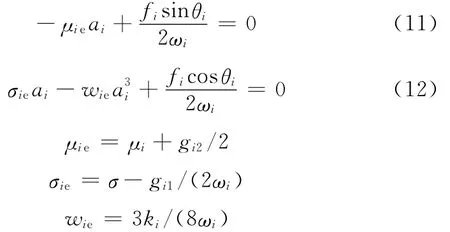
消去θi后，得

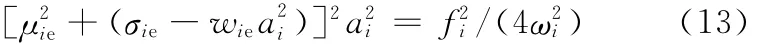
式（13）為σ與a i之間的頻率振幅響應方程。由幅頻方程可以得到系統主共振響應的峰值大小為

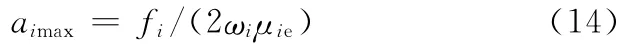
式（2）的一次近似解為

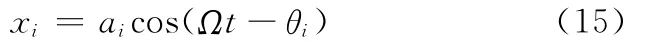
由主共振響應的峰值表達式可知，aimax與μie有關，增大μie的值，可以有效地減小aimax的值，從而達到控制非線性系統的目的。

作為對照，非線性振動系統無反饋時，非線性振動方程可以寫為［14］

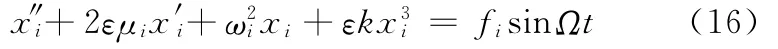
系統的σ與之間的頻率振幅響應方程為

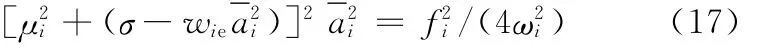
由幅頻式（17）可以得到主共振響應的峰值大小為

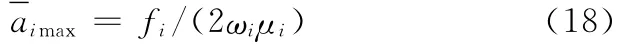
由于非線性系統通常難以求得解析解，非線性系統的減振效果不能像線性系統一樣通過響應幅值比和激勵力幅值比來討論，另外非線性系統振動與初始條件相關的穩定解具有多值性，因而研究非線性振動的減振效果較為復雜，可以通過分析主振動峰值大小的比例來分析非線性主振動的減振效果。引入非線性振動的衰減系數［15］：

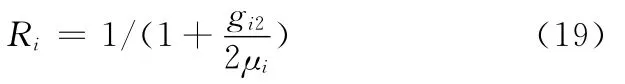
當μi與g i2同號時，g i2絕對值越大，衰減率越小，減振效果越好；反之，當μi與g i2異號時，衰減率大于1或為負值，減振器失去效果或控制失去意義。

2 主共振響應控制器設計

對于系統的非線性振動，當幅頻方程中的參數滿足一定條件時，跳躍現象、鞍結分岔和方程解的多值性等非線性現象就有可能發生，導致系統的振動變得不穩定，因而要實現非線性系統的減振控制就要避開這些不穩定因素，同時也要設計合理的控制器，減小非線性振動幅值。解的穩定性條件可以由式（11）和式（12）對應雅可比行列式的特征值而得到，其特征值λ滿足特征方程：

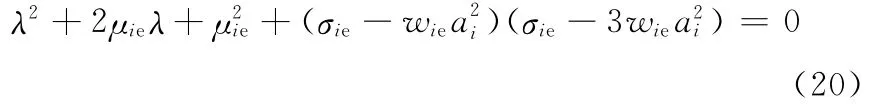
分析上式解可以得到：μie＜0，振動系統不穩定；μie＝0，特征值是一對純虛根，系統可能發生Hopf分岔；μie＞0，兩根之和恒為負。綜合分析可以得到系統穩定的充分條件［11，16］：

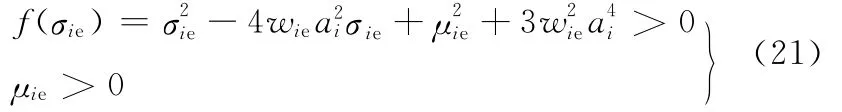
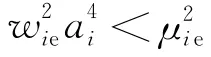
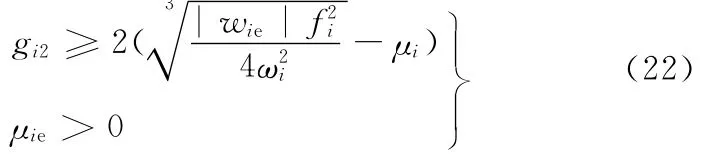
當方程f（σ）＝0有兩個實數解時，方程的解為

令

或

顯然式（21）滿足f（σ±）＞0，因而可以得到

由式（22）得到速度反饋控制參數范圍，由式（24）可以得到位移反饋控制參數范圍，據此可以設計非線性振動主共振控制器，該控制器考慮了非線性振動系統的穩定性，具有穩定的控制效果。

3 控制器參數最優化設計分析

通過對非線性振動系統的穩定性分析，我們得到反饋增益參數取值范圍，但是對系統的最佳控制參數還很難得到，為此我們進一步構造目標函數，利用最優化原理來確定最佳控制參數。

3.1 基于衰減率最優化參數設計

以非線性振動系統的衰減率為目標函數，以反饋增益參數取值范圍為約束條件，求解最佳的速度反饋參數。該模型可表示為

由上式可以計算得到速度反饋系數的數值。

3.2 基于能量最小的最優化參數設計

以非線性振動系統的能量函數為目標函數，以反饋參數取值范圍為約束條件，求解最佳的位移反饋參數。構造非線性振動系統能量函數為［17］

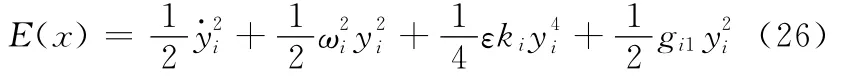
由主共振響應的一次近似解可得響應的最大值為

將式（27）代入式（26）得到能量的最值函數：

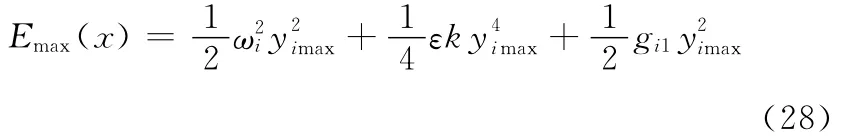
則

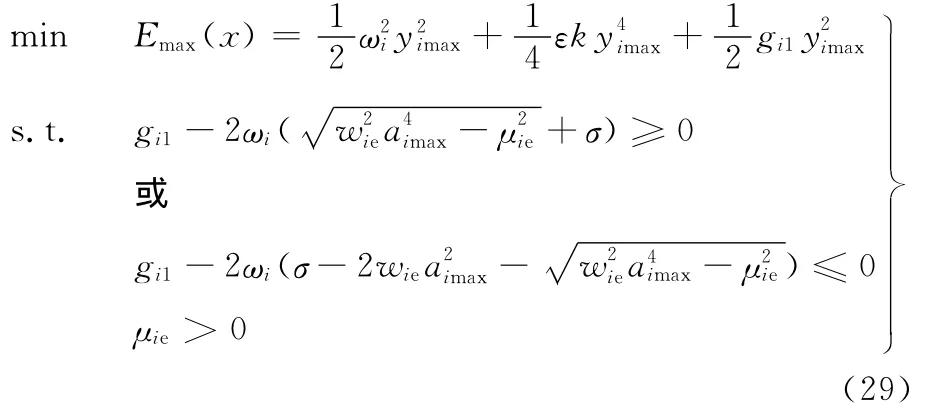
由式（25）可以求得gi2，因而可以求出μie的值，再由式（29）求得gi1的值。

4 振動阻尼測量

對于壓電傳感器，外加電場為零，當柔性梁振動時，粘貼于梁表面的壓電傳感器產生感應電荷，則壓電片上產生的輸出電壓為［18］

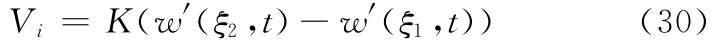
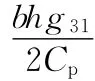
由式（30）可以得到響應峰值為

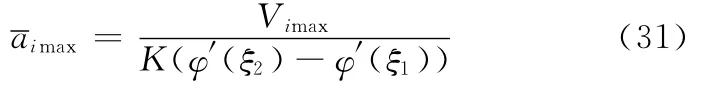
利用系統的非線性振動的幅頻方程可以確定系統的阻尼。系統無控制時，由主共振響應的峰值式（18）可以得到［19-20］：

利用上式可以得到各階模態方程對應的阻尼系數。

5 實驗分析

以粘貼壓電傳感器的懸臂梁為實驗實例，由壓電傳感器、最優化控制器和壓電驅動器組成一個閉環控制回路，對懸臂梁進行減振控制。梁的上層壓電片作為傳感器粘貼在上表面，隨著梁的振動而變形（圖1）。由壓電效應可知，隨著梁變形而縮短或伸長的壓電片會產生電壓信號，利用dSPACE采集壓電傳感器的電壓信號，送入最優化減振控制器。壓電驅動器粘貼在與壓電傳感器相同位置的梁的下表面，接收控制系統傳來的控制電壓信號，產生控制力偶矩，對梁進行減振控制。

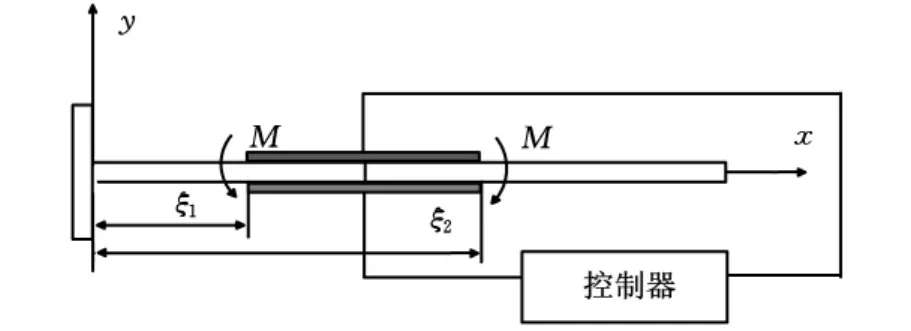
圖1 壓電懸臂梁控制系統模型

基梁為鋁材料梁，其幾何和物理參數為：長238mm，寬 50mm，高 0.93mm，彈 性 模 量E＝70GPa。壓電材料采用PZT型壓電陶瓷，壓電傳感器和驅動器的幾何和物理參數均為20mm×20mm×0.2mm，壓電片彈性模量Epe＝63GPa，g31＝10.6μV/N，Cp＝65nF。壓電感應器和驅動器的位置坐標參數均為ξ1＝15mm，ξ2＝35mm。

忽略壓電傳感器的影響，由理論計算得到懸臂梁前兩階固有頻率理論值分別為13.2788Hz、83.223Hz。通過掃頻的方式測量得到懸臂梁前兩階的固有頻率分別為16.02Hz、91.56Hz。由式（32）可以得到前兩階時域方程的阻尼系數分別為12.29和70.27。利用YE15400型激振器給懸臂梁施加一基礎振動，利用dSPACE數據采集系統采集壓電傳感器數據信號，應用MATLAB7.0快速傅里葉程序生成主共振振動圖像，由圖像讀出振動幅值電壓。由式（31）可以計算得到aimax。由式（25）計算得到前兩階穩定的速度反饋控制系數最小值分別為14.48和21.36，由于μi和g i2均為正值，由式（25）可知，gi2取值越大，衰減率越小，控制效果越好，因而為了取得較好的控制效果，反饋控制參數應盡可能取值大一些。由式（29）可以得到能量最小的前兩階位移反饋系數最大值分別為－12.28和－6.28。

利用反饋控制方法實現梁非線性主共振振動的主動控制。考慮控制系統的安全和實驗實際，一階和二階控制參數分別取為g11＝－15，g12＝55；g21＝－7，g22＝65，增益值均滿足式（22）和式（24）的要求。應用MATLAB7.0快速傅里葉程序生成振動控制圖像，如圖2～圖5所示。圖2和圖3分別為一階主共振共振時域和幅頻圖像，由圖可知，振動幅值減小了18.13dB。圖4和圖5分別是二階主共振共振時域和幅頻圖像，二階模態的位移幅值減小了11.78dB。可見，梁的前兩階模態的振動幅值都受到了明顯的抑制。

圖2 懸臂梁一階主共振響應時域圖

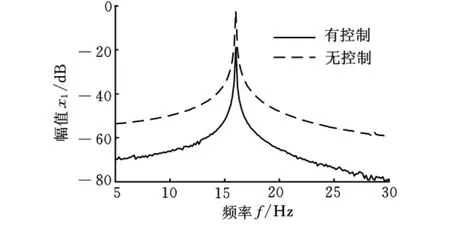
圖3 懸臂梁一階主共振響應幅頻圖

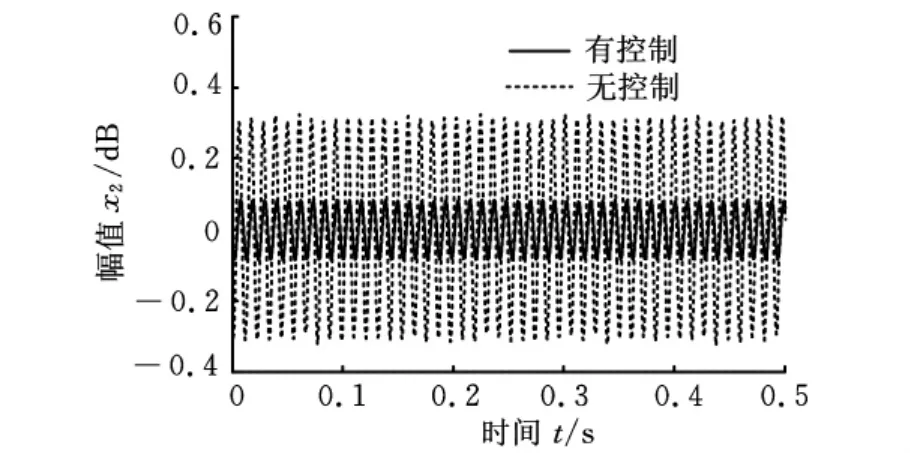
圖4 懸臂梁二階主共振響應時域圖像

6 結論

（1）本研究探索了一種基于主共振振動穩定條件的位移和速度反饋控制參數的求解方法，能夠定量地給出反饋控制參數范圍，該方法避免了以往采用嘗試法確定控制參數的弊端。應用最優化方法，得到衰減率和能量函數值最小的控制參數，該方法一方面考慮最優的減振效果，另一方面也考慮控制輸入能量和振動能量最小，有利于控制器的優化設計。

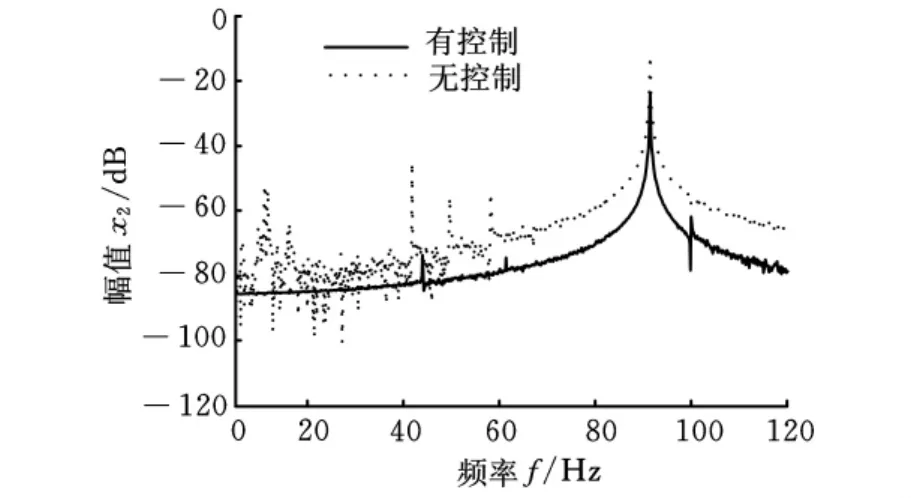
圖5 懸臂梁二階主共振響應幅頻圖

（2）該算法對應的控制器電路結構簡單，容易實現。壓電控制器控制效率高，因而該控制策略對于柔性結構的非線性振動控制具有較好優越性。

（3）該方法能較快確定有效控制參數范圍，有利于實驗參數的確定。實驗結果表明該控制方法能有效地減小主共振振動幅值，減振控制效果較好。

［1］黃建亮，黃惠儀，陳樹輝，等.梁的強非線性超、次諧波共振［J］.振動與沖擊，2004，23（1）：1－3.

Huang Jianliang，Huang Huiyi，Chen Shuhui.Superharmonic and Subharmonic Resonances of Strongly Nonlinear Vibration of Beams［J］.Journal of Vibration and Shock，2004，23（1）：1－3.

［2］袁尚平，張建武，王慶宇.薄板3倍超諧振動的分析與試驗［J］.上海交通大學學報，2001，35（7）：955－961.

Yuan Shangping，Zhang Jianwu，Wang Qingyu.Analysis and Experiment on 3－times Superharmonic Resonance of Thin－plate［J］.Journal of Shanghai Jiaotong University，2001，35（7）：955－961.

［3］Amabili M.Nonlinear Vibrations of Rectangular Plates with Different Boundary Conditions：Theory and Experiments［J］.Computers and Structures，2004，82：2587－2605.

［4］李韶華，楊紹普.采用改進Bingham模型的非線性汽車懸架的主共振［J］.振動與沖擊，2006，25（4）：109－111.

Li Shaohua，Yang Shaopu.Primary Resonance of a Nonlinear Vehicle Suspension System Using a Modified Bingham Model［J］.Journal of Vibration and Shock，2006，25（4）：109－111.

［5］馮霏，李凌軒，陳亞哲，等.汽車非線性懸架系統共振特性的研究［J］.東北大學學報（自然科學版），2010，1（3）：415－417.

Feng Fei，Li Lingxuan，Chen Yazhe，et al.Research on Resonance Characteristics of Nonlinear Suspension System of Motor Vehicles［J］.Journal of Northeastern University（Natural Science），2010，1（3）：415－417.

［6］丁虎，陳立群.軸向運動黏彈性梁橫向非線性受迫振動［J］.振動與沖擊，2009，28（12）：128－131.

Ding Hu，Chen Liquan.Transverse Non－linear Forced Vibration of Axially Moving Viscoelastic Beam［J］.Journal of Vibration and Shock，2009，28（12）：128－131.

［7］趙艷影，徐鑒.時滯非線性動力吸振器的減振機理［J］.力學學報，2008，40（1）：98－105.

Zhao Yanying，Xu Jian.Mechanism Analysis of Delayed Nonlinear Vibration Absorber［J］.Chinese Journal of Theoritical and Applied Mechanics，2008，40（1）：98－105.

［8］Alhazza K A，Nayfeh A H，Daqaq M F.On Utilizing Delayed Feedback for Active Multi－mode Vibration Control of Cantilever Beams［J］.Journal of Sound and Vibration，2009，31（9）：735－752.

［9］Nayfeh A H，Nayfeh S A.On Nonlinear Modes of Continuous Systems［J］.Journal of Vibration and Acoustics，1994，116：129－136.

［10］Daqaq M F，Alhazza K A，Arafat H N.Nonlinear Vibrations of Cantilever Beams with Feedback Delays［J］.International Journal of Non－linear Mechanics，2008，43：962－978.

［11］Li X Y，Ji J C，Hansen C H，et al.The Response of a Duffing－van der Poloscillatorunder Delayed Feedback Control［J］.Journal of Sound and Vibration，2006，291：644－655.

［12］Qian C Z，Tang J S.A Time Delay Control for a Non－linear Dynamic Beam under Moving Load［J］.Journal of Sound and Vibration，2008，309：1－8.

［13］Alhazza K A，Daqaq M F，Nayfeh A H，et al.Nonlinear Vibrations of Parametrically Excited Cantilever Beams Subjected to Non－linear Delayed－feedback Control［J］.International Journal of Non－linear Mechanics，2008，43：801－812.

［14］胡海巖.應用非線性動力學［M］.北京：航空工業出版社，2007.

［15］Ji J C，Zhang N.Suppression of the Primary Resonance Vibrations of a Forced Nonlinear System Using a Dynamic Vibration Absorber［J］.Journal of Sound and Vibration，2010，329：2044－2056.

［16］黃濤，樊建平，何建平，等.非線性彈簧汽車懸架系統的非線性振動機理研究和運動穩定性分析［J］.中國機械工程，2007，18（15）：1882－1885.

Huang Tao.Fan Jianping，He Jianping，et al.Dynamic Characteristics and Motion Stability Analysis of Vehicle Suspension with Nonlinear Spring［J］.China Mechanical Engineering，2007，18（15）：1882－1885.

［17］李驪，葉紅玲.強非線性系統周期解的能量法［M］.北京：科學出版社，2008.

［18］Narayanana S，Balamurugan V.Finite Element Modeling of Piezolaminated Smart Structures for Active Vibration Control with Distributed Sensors and Actuators［J］.Journal of Sound and Vibration，2003，262（3）：529－562.

［19］劉延柱，陳文良，陳立群.振動力學［M］.北京：高等教育出版社，1998.

［20］Pramod Malatkar.Nonlinear Vibrations of Cantilever Beams and Plates［D］.Blacksburg，Virginia：Virginia Polytechnic Institute and State University，2003.