讓聯(lián)系在課堂教學中大放光彩——《正弦定理》的課堂實錄

☉浙江省象山中學 祝益鋒

數(shù)學學科是一個不可分割的整體，聯(lián)系是數(shù)學知識結(jié)構(gòu)的本質(zhì).中學數(shù)學中眾多的“知識點”并非彼此孤立地存在著，而是充滿錯綜復(fù)雜“多方位”的聯(lián)系.既然數(shù)學知識是結(jié)構(gòu)化的知識，在數(shù)學教學中，教師就應(yīng)把知識間的聯(lián)系如實地展示出來，使學生獲得數(shù)學理解的同時，充分認識其內(nèi)在的聯(lián)系；并且只有通過平時教學的經(jīng)常聯(lián)系，學生才能逐漸地樹立起整體聯(lián)系的觀點，學到結(jié)構(gòu)化的、互相聯(lián)系的數(shù)學知識，為形成和發(fā)展良好的數(shù)學認知結(jié)構(gòu)打下基礎(chǔ).

但是，由于知識在教材中的呈現(xiàn)相對獨立，且教學內(nèi)容以課時為單位設(shè)計學習，加之學生認知發(fā)展的局限，知識的聯(lián)系往往被“隱藏”起來，在沒有教師引領(lǐng)的情況下，學生不易發(fā)現(xiàn)知識之間的關(guān)聯(lián)，看到的只是零碎的顯性知識.教師在教學過程中，如何根據(jù)知識的發(fā)展和學生的認知規(guī)律，精心選擇教學材料，從而構(gòu)建聯(lián)系組織教學.對于這一問題，本文以“正弦定理”的教學實錄為例，談?wù)勛约旱膶嵺`與思考.

一、認知聯(lián)系：創(chuàng)設(shè)矛盾情境，引發(fā)認知沖突

眾所周知，教學關(guān)系不是靜態(tài)固定的，而是動態(tài)變化的.從學生角度來說，教學過程是一個“從教到學”的轉(zhuǎn)化，是在教師的作用下學習能力不斷提高的過程.因此，在“教”與“學”的關(guān)系中，“教”是為幫助“學”而存在，但在如何幫助“學”上存在兩種教學思路，一種是著眼于學生的無知，關(guān)注學生不會什么，于是迫不及待地用自己已掌握的學科知識去填補他的空白.這樣的教學，將數(shù)學知識的構(gòu)建產(chǎn)生的生動過程變成機械的連鎖學習，枯燥而乏味；另一種是著眼于學生的認知，關(guān)注學生已會了什么，尊重他們的認知，適當?shù)貙ⅰ奥?lián)系”貫穿于教學之中，引導(dǎo)他們把握數(shù)學知識的內(nèi)在聯(lián)系，有效促進學生把數(shù)學知識結(jié)構(gòu)內(nèi)化為自己的認知結(jié)構(gòu)，提高對數(shù)學整體性的認識.

師（幾何畫板演示）：如圖1，已知點C在弦AB所對的優(yōu)弧上運動，請分析，在△ABC中，邊與角分別有哪些關(guān)系成立？

學生易發(fā)現(xiàn)，①A+B+C=π；②大邊對大角；③角C的對邊c保持不變.

圖1

師：我們發(fā)現(xiàn)在△ABC中，有角C的對邊c保持不變，角A，B與它們的對邊a，b卻在不斷地變化，大家覺得這“變”與“不變”中是否存在某種確定的數(shù)量關(guān)系呢？

數(shù)學教學是數(shù)學活動的教學，它不僅在于讓學生學會某個知識點，掌握一定的知識與技能，更應(yīng)是一個創(chuàng)造思維的起點，一個創(chuàng)新意識的啟動.在某些數(shù)學知識的背后，往往有著學生已經(jīng)掌握的舊知或者生活經(jīng)驗作為基礎(chǔ).表面上，教師設(shè)計問題情境的目的，在于喚醒學生對初中有關(guān)三角形的一些知識的記憶，為學生提供基于最近發(fā)展區(qū)的學習支持；但更重要的是通過向?qū)W生提供豐富的、典型的背景材料，以矛盾誘發(fā)認知沖突，創(chuàng)設(shè)激活知識間聯(lián)系的情境，激發(fā)學生探究新知的欲望：“變”與“不變”中是否存在某種確定的數(shù)量關(guān)系呢？

二、建立聯(lián)系：提出猜想，促進認知順應(yīng)

學生是信息加工的主體，是意義的主動建構(gòu)者，在其原有認知結(jié)構(gòu)已無法“容納”新的對象時，他們就必須對已有的認知結(jié)構(gòu)進行變革，以求與客體相適應(yīng)，達到新的“平衡”，即為所謂的“順應(yīng)”.建構(gòu)主義學習觀認為：學習不是被動地接受外部知識，而是根據(jù)自己的經(jīng)驗背景，對外部信息進行選擇、加工和處理，從而獲得心理意義．教師作為意義建構(gòu)的幫助者與促進者，應(yīng)利用已經(jīng)生成的認知沖突，學生膨脹的探索欲望，給學生提供足夠的時間和空間，通過合理的數(shù)學活動，順勢引導(dǎo)學生運用數(shù)學知識與方法，如變化、特殊化、聯(lián)系等觀點的內(nèi)在思想性，使學生經(jīng)歷知識的“再發(fā)現(xiàn)”，在感悟知識聯(lián)系的挑戰(zhàn)中，將數(shù)學知識與思想方法融為一體，獲得結(jié)果.

師：許多數(shù)學問題，雖然我們對其表現(xiàn)形式可能陌生，但其本質(zhì)總存在著簡單的一面.因此，我們不妨實施“特殊化”的策略，從一般退到特殊進行探究，發(fā)現(xiàn)問題可能的一般性結(jié)論.

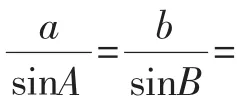
師：很好！我們將任意三角形特殊化為直角三角形，得到了一個漂亮的結(jié)果!我思故我在，對知識我們應(yīng)該思考不止，探索不已.它是否能推廣為更具價值的一般性結(jié)論呢？

師（贊許）：你什么時候?qū)W會了“順桿爬”了？你的回答，既體現(xiàn)了數(shù)學知識從特殊到一般的歸納形成過程，也體現(xiàn)我們對問題的一個合理化猜想.大家能證明這個結(jié)論嗎？

蘇霍姆林斯基說，“在人的心靈深處，都有一種根深蒂固的需要，這就是希望感到自己是一個發(fā)現(xiàn)者、研究者和探索者，而在兒童的精神世界，這種需要特別強烈.”因此，教學中應(yīng)以研究為主線，引導(dǎo)學生展開積極的、合理的猜想，是學生“再發(fā)現(xiàn)”、“再創(chuàng)造”知識的良好開端.同時，數(shù)學知識的內(nèi)在聯(lián)系表現(xiàn)在：數(shù)學知識相互滲透，形成基本的數(shù)學思想方法，使之融合為具有特定規(guī)律的知識體系，這也決定了數(shù)學教學不能停留在知識的顯性聯(lián)系上，把知識背后的隱性聯(lián)系——數(shù)學思想方法貫穿其中，做到既見其“表”又入其“里”，使學生在感悟數(shù)學知識間的相互聯(lián)系的同時，實現(xiàn)數(shù)學思維和認知能力的飛躍.

三、感悟聯(lián)系：證明猜想，促進知識同化

聯(lián)系的觀點之形成和發(fā)展，需要有一個不斷加深認識的過程.布魯納的發(fā)現(xiàn)學習論認為，“認知是一個過程，而不是一種產(chǎn)品.”但在實際的教學活動中，我們常將形成結(jié)論的生動過程變成單調(diào)的反復(fù)演練，希望通過“大容量、高密度”的強化訓練，加深對知識的理解，這固然對鞏固知識有很大的效果，但相對而言，這只是表層認識，對知識的整體性理解作用甚微.所以無論是從特殊到一般的數(shù)學知識的歸納形成過程，還是從一般到特殊的數(shù)學知識的驗證應(yīng)用過程，教師應(yīng)鼓勵學生積極思考、有效交流，并適當予以方法指引，探究證明猜想，引導(dǎo)學生發(fā)現(xiàn)猜想與已有數(shù)學知識的內(nèi)在聯(lián)系，挖掘其中的數(shù)學思想方法，促進學生把數(shù)學知識內(nèi)化為自己的認知結(jié)構(gòu)，使學生建立更深層次的聯(lián)系觀念.

生：如圖2，不妨設(shè)△ABC中最大角為角A.作直徑AD，連結(jié)BD，CD.在Rt△ABD中，AB=2RsinC；在 Rt△ACD中，AC=2RsinB.

圖2

圖3

作直徑BE，連接CE.由圓內(nèi)接四邊形的性質(zhì)，可知若A為銳角，有∠BEC=A（如圖2）；若A為鈍角，有∠BEC=180°-A（如圖 3），所以，在 Rt△BCE中，BC=2Rsin∠BEC=2RsinA.

師（總結(jié)）：不錯！將任意三角形轉(zhuǎn)化為直角三角形來研究，這恰好也體現(xiàn)了從一般到特殊的思維方式.

師生共同總結(jié)正弦定理：在一個三角形中，各邊和它所對角的正弦的比相等，即

《數(shù)學課程標準》指出，“有效的數(shù)學學習過程不能單純地依賴模仿與記憶，教師應(yīng)引導(dǎo)學生主動地從事觀察、實驗、猜測、驗證、推理與交流等數(shù)學活動”.在教學中，從知識層面上，教師的主要作用在于激發(fā)學生的學習熱情，再現(xiàn)知識的形成和生長過程，揭示知識間的聯(lián)系，加深學生對所學知識的理解，促進學習有效地進行；從情感與價值觀層面上，讓學生在獲得知識的過程中，更深刻地體會從特殊到一般、從具體到抽象的認知規(guī)律；培養(yǎng)大膽猜想、小心求證的理性精神，逐步形成自主學習的能力.

四、溝通學科聯(lián)系：聯(lián)想物理知識，深化知識

教學是教與學的交往、互動，它不是教師教與學生學的機械疊加，而是形成一個真正的“學習共同體”.在教學中，師生分享彼此的思想，以豐富教學內(nèi)容，求得新的發(fā)現(xiàn)，從而實現(xiàn)教學相長和共同發(fā)展.在數(shù)學教學中，教師應(yīng)重視生成性教學，敏銳地捕捉課堂上的生成性資源，依據(jù)知識之間的邏輯關(guān)系和遷移條件，幫助學生理解內(nèi)化新知，揭示知識間的內(nèi)在聯(lián)系，構(gòu)建更高層次的知識體系.

師：有沒有其他辦法證明正弦定理呢？

教師本來預(yù)設(shè)的方案是引導(dǎo)學生用三角形的面積公式證明正弦定理，正如布盧姆所言，“人們無法預(yù)料到教學所產(chǎn)生的成果的全部范圍.”沉默中，突然一名學生興奮地叫了起來：“這個正弦定理的形式不是與力學中的拉密定理完全一樣嗎？”所有的同學都被他的想法所吸引.

師：你真善于聯(lián)想，確實這形式就是拉密定理！拉密定理的內(nèi)容是什么？物理學中怎么證明的？

生：在同一平面內(nèi)，當三個共點力的合力為零時，其中任一個力與其他兩個力夾角正弦的比值相等.證明方法？……好像用到了力的正交分解.

師（引導(dǎo)）：嗯，物理學上力的正交分解，實際上也就是數(shù)學中什么方法？

生（遲疑中回答）：在直角坐標系中研究——坐標法.

師：對，我們常借助坐標系研究幾何問題，我們能否利用坐標法證明正弦定理呢？

學生動手建立坐標系，并表示出相應(yīng)點的坐標.

師：如圖 4所示，將△ABC置于直角坐標系中，并作ADBC.請你思考：你能寫出點C與點D的坐標嗎？隨著角A從銳角變化到鈍角，點C與點D坐標的表示形式會發(fā)生變化嗎？

學生順利地寫出C（bcosA，bsinA），D（acos（π-B），asin（π-B）），即D（-acosB，asinB）.

師：由四邊形ABCD為平行四邊形，我們能想到什么呢？

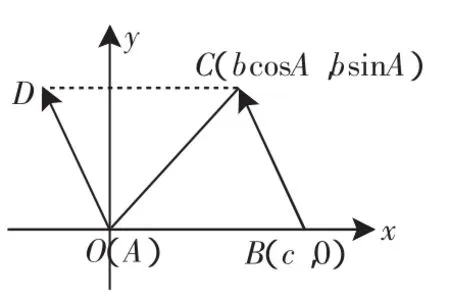
圖4

師（總結(jié)）：我們可以看出，由坐標法，拉密定理其實是正弦定理的外角表示形式.正弦定理的證明過程與其說是令人驚奇，不如說是知識間聯(lián)系的絕妙.在數(shù)學學習的過程中，注重數(shù)學知識的理解和領(lǐng)會知識間的聯(lián)系，這樣才能真正把握數(shù)學知識的本質(zhì)，提高自己的能力.這種證明方法的優(yōu)點是避免了繁雜的分類討論，雖然我們對坐標法接觸不多，但在學習解析幾何后，可以進一步體會坐標法解決幾何問題的優(yōu)越性.

在數(shù)學教學中，教師往往只注重精煉的、本質(zhì)的邏輯結(jié)論的應(yīng)用教學，對數(shù)學知識的整體性和知識的相互聯(lián)系缺乏必要的組織，其形成和發(fā)展過程被簡單化，學生很難理解其中的“源”與“流”，而造成知識間互相閉鎖，聯(lián)系人為割裂.其實，數(shù)學知識的聯(lián)系不僅表現(xiàn)為學科內(nèi)部系統(tǒng)的單向聯(lián)系，還有學科間的多向的交叉聯(lián)系.學生原有知識結(jié)構(gòu)中也不乏能用數(shù)學的眼光去審視的問題，而他們?nèi)鄙俚模蚴且痪涔奈璧脑挘蚴且桓更c方向的手指.這就要求教師在教學中，關(guān)注課堂內(nèi)“預(yù)設(shè)”之外“生成”，發(fā)揮學生對知識加工的自主性，“就湯下面”，從學生認知數(shù)學知識角度與方式，在大學科的背景中把握教學內(nèi)容，拓展學生知識建構(gòu)的途徑，讓數(shù)學學習生動而深刻.

五、深化聯(lián)系：構(gòu)建知識網(wǎng)絡(luò)

在數(shù)學教學中，學習活動是否有效，主要看新的學習內(nèi)容能否與學習者認知結(jié)構(gòu)中原有的知識系統(tǒng)建立實質(zhì)性的聯(lián)系.因此，數(shù)學教學中不應(yīng)追求知識的“一步到位”，而應(yīng)體現(xiàn)知識發(fā)展的階段性，符合學生的認知規(guī)律；不應(yīng)過早地將知識“符號化”，而應(yīng)延長知識的生長過程，讓學生充分經(jīng)歷研究的樂趣；不應(yīng)追求解決方法“統(tǒng)一化”和“最佳化”，而應(yīng)致力于“多樣化”與“合理化”，建立知識的深層聯(lián)系.這需要教師引導(dǎo)學生通過類比、歸納、聯(lián)想等思維活動，促進學生數(shù)學認知結(jié)構(gòu)的形成與發(fā)展，培養(yǎng)學生深刻的思維品質(zhì).

師：受上面證明方法的啟發(fā)，既然我們聯(lián)想到向量，使向量作為工具去證明正弦定理也成為可能，那么你會證明嗎？

在學生沉思無果時，教師適時提示：在我們所學過的向量知識中，有什么知識同時涉及長度和三角函數(shù)？

學生指出平面向量的數(shù)量積.

師：請大家回憶，向量的運算中，哪種運算與三角形有關(guān)？

生：向量的加法和減法滿足三角形法則，如：

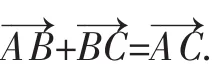
師（追問）：e應(yīng)具有什么特征呢？

所以，e為與AB垂直的非零向量，其模可以是任意大小.

“教學的藝術(shù)不在于傳授本領(lǐng)，而在于激勵、喚醒和鼓舞.”實踐證明，教學中，教師及時抓住知識的連接點、生長點，誘發(fā)學生對一個數(shù)學問題從多方位、多角度去探索聯(lián)想，引導(dǎo)學生努力挖掘知識的相關(guān)性、相通性和綜合性，加強知識的橫向聯(lián)系，有利于學生理解定理的實質(zhì)和公式的含義，形成對基礎(chǔ)知識系統(tǒng)化的認識；提高學生的思維能力，激發(fā)學習興趣.經(jīng)常突出“聯(lián)系”的觀點，還可使學生突破原有的思維模式和常規(guī)的范圍，在聯(lián)系中有發(fā)現(xiàn)，在發(fā)現(xiàn)中有發(fā)展.

六、知識的應(yīng)用

在數(shù)學教學中，解題是教學活動的重要組成部分，其目的不只是強化結(jié)論識記，更重要的是學生通過對數(shù)學對象的思維構(gòu)造，綜合調(diào)用數(shù)學知識，多方位建立具體問題與認知結(jié)構(gòu)中知識間的本質(zhì)聯(lián)系，將習得的知識遷移到新情境中去解決問題的一個具體化過程，是知識的又一次“升華”.

師：聯(lián)想其他知識，正弦定理還可以利用面積法證明.請大家課下自行研究.下面我們來歸納正弦定理的結(jié)構(gòu)特征與應(yīng)用.這個定理在結(jié)構(gòu)上有何特征？

生：各邊與其對角的正弦互相對應(yīng)，體現(xiàn)數(shù)學的對稱美.

師：學習正弦定理有什么用呢？先讓我們來了解一下“解三角形”的概念：一般地，把三角形的三個角A，B，C和它們的對邊a，b，c叫做三角形的元素.已知三角形的幾個元素，求其他元素的過程叫做“解三角形”.正弦定理是解三角形的重要工具之一.如果用方程的觀點認識正弦定理，那么在六個元素中需要知道幾個量，才能求出其他量？

例：已知D為等腰△ABC底邊BC上一點，試判斷△ABD和△ACD的外接圓的半徑大小.

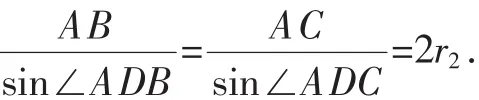
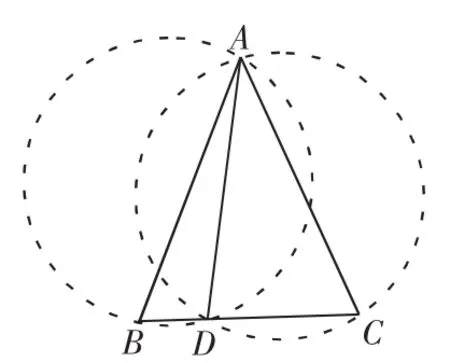
圖5

課堂練習與知識小結(jié)環(huán)節(jié)（略）.

解題作為數(shù)學學習的重要手段，通過解題引導(dǎo)學生外顯的推理演算與內(nèi)隱的邏輯思考相結(jié)合，加深對數(shù)學知識的理解，有助于知識間聯(lián)系的豐富與鞏固；通過解題，使知識的理解更具生成性，學習心理學表明，新信息若能納入到已有的知識體系中，會使原有的理解不斷拓展、深化，產(chǎn)生新的理解，有助于知識間聯(lián)系的擴展與調(diào)整，因此，例題的選擇與教學也應(yīng)注意貫穿“聯(lián)系”的觀點，有效促進學生把數(shù)學知識結(jié)構(gòu)內(nèi)化為自己的認知結(jié)構(gòu).

七、結(jié)語

“注重聯(lián)系，提高（學生）對數(shù)學整體的認識”是《數(shù)學課程標準》的教學建議之一.它還認為，“要注重數(shù)學的不同分支和不同內(nèi)容之間的聯(lián)系，數(shù)學與日常生活的聯(lián)系，數(shù)學與其他學科的聯(lián)系”.數(shù)學知識間的聯(lián)系，不單表現(xiàn)在鄰近概念的聯(lián)系，或知識的表層聯(lián)系與單向聯(lián)系，在數(shù)學教學中，更應(yīng)引導(dǎo)學生對學習內(nèi)容進行多向聯(lián)系和深層次的聯(lián)系.如果拋開聯(lián)系的觀點去學習數(shù)學定義、定理、公式、法則，那么數(shù)學學習將淪為死記硬背式的學習，且極易遺忘.實踐證明，只有理解知識間的內(nèi)在聯(lián)系，從聯(lián)系中發(fā)現(xiàn)內(nèi)在規(guī)律，領(lǐng)悟含于其中的數(shù)學基本思想方法，使認識不斷“升華”，這樣才能在聯(lián)系中理解，在理解中記憶，這樣的記憶才能保持，即使遺忘，通過聯(lián)想（聯(lián)系）也能再現(xiàn)，這樣才能教得自由，學得主動.

過程因探究而精彩，知識因聯(lián)系而生動.總之，在教學中，發(fā)掘數(shù)學知識之間的內(nèi)在聯(lián)系是一項復(fù)雜而繁重的任務(wù)，需要我們在平時的教學中不斷地深思探索，使學生理解數(shù)學知識的整體性，知曉數(shù)學方法的一般性.