解讀導數背景下的“參數分離”

☉江蘇省丹陽高級中學 陳曦遠

含參變量的不等式恒成立問題是歷年高考的熱點，也是難點，在各省市高考命題中屢見不鮮，且常考常新.此類問題綜合性較強，融函數、導數、不等式等高中數學主干知識為一體，能有效考查考生的綜合解題能力，在培養學生思維的靈活性、創造性方面起到了舉足輕重的作用.在眾多的求解方法中“分離參數”法的作用不容忽視.本文以導數背景下的不等式恒成立問題為例，談談“分離參數”法的應用.

一、參數的直接分離

例1 已知函數f（x）=lnx-ax+1，a∈R是常數.討論函數y=f（x）零點的個數.

當x=1時，g（x）的最大值為g（1）=1.

所以若a＞1，則f（x）無零點；

若f（x）有零點，則a≤1.

若a=1，f（x）=lnx-ax+1=0，易知f（x）有且僅有一個零點x=1.

若a≤0，f（x）=lnx-ax+1單調遞增，由冪函數與對數函數的單調性比較，知f（x）有且僅有一個零點（或：直線y=ax-1與曲線y=lnx有一個交點）.

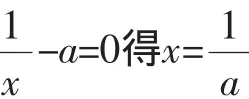
綜上所述，當a＞1時，f（x）無零點；當a=1或a≤0時，f（x）有且僅有一個零點；當0＜a＜1時，f（x）有兩個零點.

點評：本題原為考查零點的個數問題，經參數直接分離后即轉化為函數與直線交點個數問題，進而使問題輕松獲解.

二、導函數中的參數分離

例2 已知函數f（x）=x2+2alnx.

（1）求函數f（x）的單調區間；

解析：（1）略.

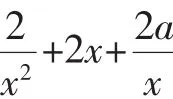
點評：題目中若給出函數在某區間內的單調性，則問題轉化為導函數在該區間內恒大于（小于）0，進而再進行參數分離求解即可.

三、整體思想下的參數分離

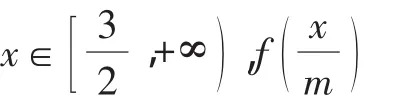
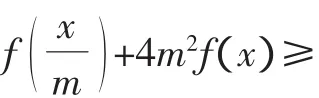
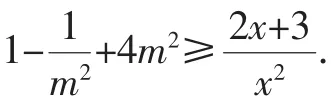
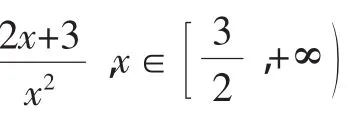
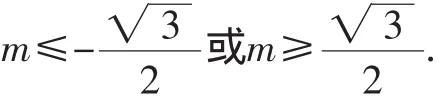
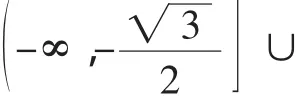
點評：分離出來的參數，有些時候并不是以單獨的字母的形式出現，而是一個關于參數的函數式g（m），如g（m）≤f（x）或g（m）≥f（x）的形式，解題思路是先求出f（x）在給定的區間上的最值，即有g（m）≤fmin（x），g（m）≥fmax（x）.

四、自變量的取值范圍決定了參數是否能順利分離

例4 設函數f（x）=ax3-3x+1，（x∈R），若對任意的x∈［-1，1］，都有f（x）≥0成立，則實數a的值為______.

解析：由ax3-3x+1≥0，得ax3≥3x-1.因x∈R，故分離參數a，需根據x的取值進行分類討論，如下：

（1）當x=0時，f（x）=1＞0恒成立，a可以取任意實數；

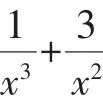
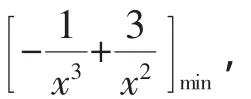
綜上可得a=4.

點評：本題在參數分離的過程中，要在不等式兩邊同時除以x才能實現參數的分離，若x的取值范圍在正數區間上，可以避免討論；若x的取值范圍中包含零或者負數，則需要進行分類討論.

五、函數最值的存在性決定參數取值區間的開或閉

A.［-1，+∞）B.（-1，+∞）C.（-∞，-1］D.（-∞，-1）

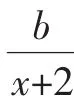
函數g（x）=x（x+2）在區間（-1，+∞）上的值域為（-1，+∞），不存在最小值-1，故b的值可以為-1，即b≤-1，答案為C.

例6 已知函數f（x）=x2-3x，當x∈（0，+∞）時，不等式f（x）＞ax-1恒成立，則實數a的取值范圍為__________.

點評：參數的取值范圍必然涉及區間的開或閉，起決定因素的是不等號以及函數最值的存在性.比如a≤f（x），f（x）的最小值是fmin（x），則a≤fmin（x）；當f（x）沒有最小值，但接近一個常數m，則a≤m.又如a＜f（x），f（x）的最小值是fmin（x），則a＜fmin（x）；當f（x）沒有最小值，但接近一個常數m，則a≤m.

綜上所述，本文簡述了解不等式恒成立問題中“分離參數”法的應用，此法是求解不等式“恒成立”問題的基本應對策略.教師在實際教學中還應注重培養學生對解題方法的提煉，經常引導學生梳理知識，形成知識板塊和方法體系，真正提高學生分析問題和解決問題的能力.