基于荷載結構原理的隧道結構可靠度研究

趙懷東

(山西焦煤集團有限責任公司 計劃發展部，山西 太原030024)

1 隧道工程結構的設計模型

地下工程的設計理論和方法經歷了一個相當長的發展過程。早在19 世紀初期，地下工程（包括隧道和地下洞室）對以磚石作為襯砌，用木支撐的分布開挖方法進行施工， 這樣設計的襯砌結構的厚度偏大。隨著社會的發展，科學技術的不斷進步，地下工程的科技人員提出了不同的設計計算方法。 如溫克爾提出了局部變形理論，假定了圍巖對襯砌結構的抗力的大小與襯砌結構本身的變形大小成正比；還有將襯砌和圍巖作為一體的連續介質設計分析模型，用彈性力學的方法進行分析。 20 世紀50 年代，在地下工程的修建中，噴射混凝土和錨桿作為初期支護得到了廣泛應用，這樣的柔性支護使開挖后的洞室圍巖有一定的變形，圍巖內部的應力重新分布，但是圍巖能夠發揮自穩性，這樣可以大大減小襯砌結構的設計厚度。 20 世紀60 年代，隨著計算機的發展和巖土本構關系的建立，地下工程結構的設計分析進入了以有限元為主的計算機數值模擬分析時期。

國際隧道協會于1978 年成立了結構設計模型研究小組， 收集了各會員國所采用的地下工程結構設計模型[1-2]（如表1）。

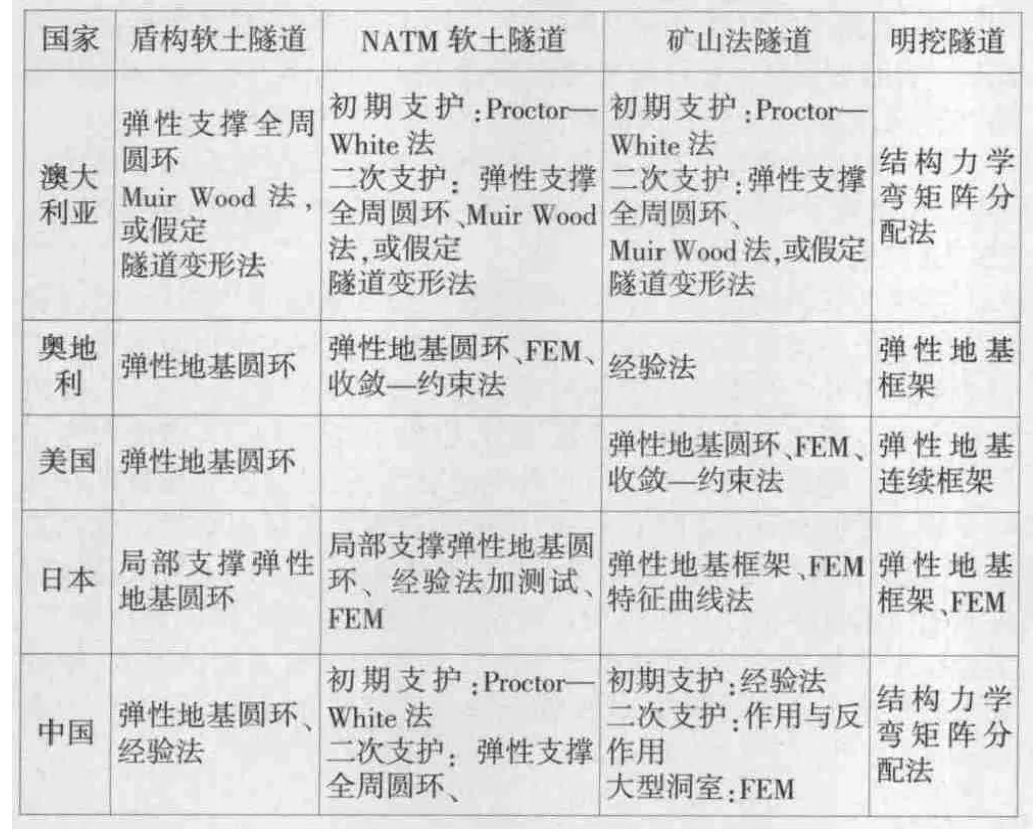
表1 隧道及地下工程結構設計模型

其中： NATM——新奧法（New Austria Tunneling Method）

FEM——有限元法（Finite Element Method）

2 隧道襯砌荷載效應的隨機有限元原理

2.1 基本假定

假定襯砌為小變形梁，襯砌為足夠多個離散等厚度直梁單元。

用布置于模型各節點上的彈簧單元來模擬圍巖與結構的相互作用性，彈簧單元不承受拉力，受拉力將自動脫落，彈簧的彈性系數由Winkler 假定為基礎的局部變形理論確定， 一般采用地層的彈性抗力系數K 值，再計算得出模擬結構與地層相互作用間彈簧的彈性系數。

拱底作用相同的豎向反力來平衡地面荷載、土壓以及結構自重。

因為隧道是細長結構，采用平面應變模式進行分析[3]。

2.2 隨機有限元基本原理

在整體坐標系下，有限元方法的基本公式如下：

其中K、U、F 分別為剛度矩陣、位移、荷載向量。

當材料性質、幾何尺寸和荷載作用具有隨機變化的性質時上式就成為具有隨機性質的矩陣位移分量的隨機有限元表達式

設具有隨機變化性質的某一參數Z 用一個確定值Z0和一個隨機擾動動量αZ0的和來表示，即Z=Z0(1+α)。 其中α 為均值為零的隨機場，反映了參數Z 的隨機性。 Z0一般為均值。 將α 離散化為隨機向量{α}，則函數K、U、F 為隨α 而變的隨機函數，將分別在α=0 處按泰勒級數展開，略去二階以上的項，則有：

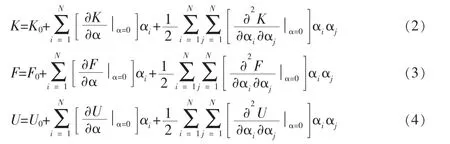
式中：N 表示隨機變量的總數，上式帶入上上式，略去含有3、4 階項，并運用二階攝動法即可得到如下的遞推公式：

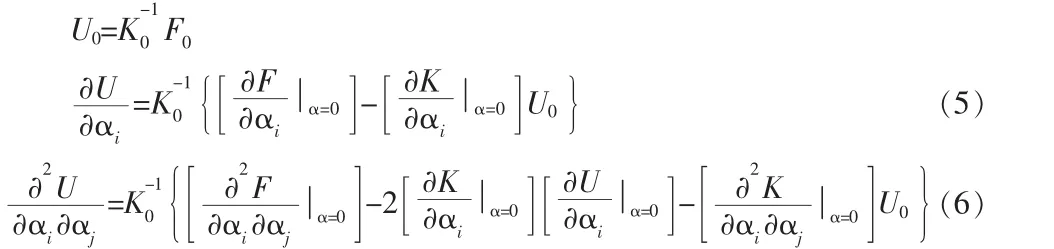
在求出對α 的二階微分后，便可以求出節點位移的均值和方差：

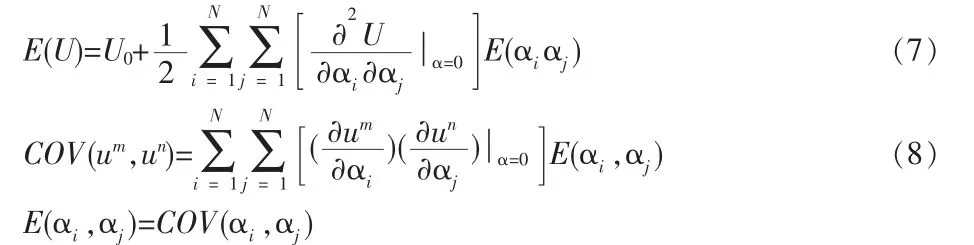
其中um和un分別為U 的第m 個和第n 個分量。 同樣，由內力與位移的關系可求得內力得均值和協方差[4]。

3 隨機有限元法計算結構可靠度的步驟

利用隨機有限元計算襯砌結構可靠度的步驟如下：

1）建立功能極限函數

對于隧道結構可靠度而言，采用最大抗拉強度，單元極限狀態方程為：

g(x)=R(x)-S(x)=σL-σ1

其中，σL—為材料的抗拉強度

σ1—為單元的最大拉應力

2）劃分網格，建立離散化模型

隨機有限元法分析結構結構的可靠度，需要將隨機場離散化為隨機場單元，其劃分網格的方法和要求與有限元計算類似，除了需要考慮物體內部應力變化的劇烈程度以外，還要考慮物體內部隨機場（或隨機變量）的變異性和相關結構。一般來說，隨機場單元與有限單元可以共享一套網格，一個隨機場單元可以包含若干個有限單元，以便減少計算工作量。

3）準備數據信息。 輸入基本變量的均值、標準差等。

4）進行隨機變量抽樣。

5）代入上述計算公式，計算安全余量。

6）迭代計算可靠指標。

4 計算實例

設混凝土襯砌隧洞的橫截面如圖1 所示，其內半徑ri=3.0m，襯砌厚度0.5m，埋深25m，承受0.5MPa 的荷載作用，各隨機變量及其統計特征見表2。

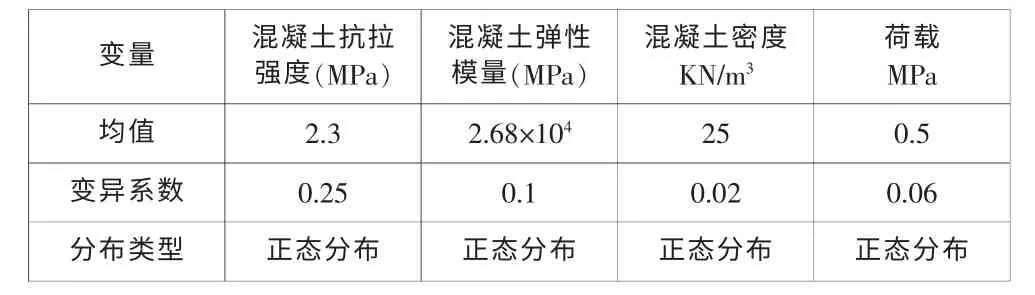
表2 隨機變量及其統計特征

泊松比取為定植，圍巖取值0.25。在邊界荷載下，計算隧洞周邊各單元的可靠指標。

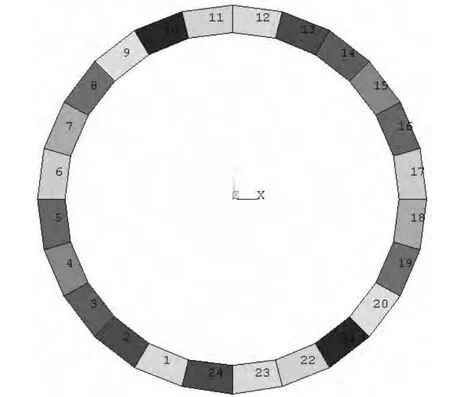
圖1 混凝土襯砌單元圖

采用四節點等參隨機有限元法計算，由于結構的對稱性，左邊算得的結構可靠指標列于表3：

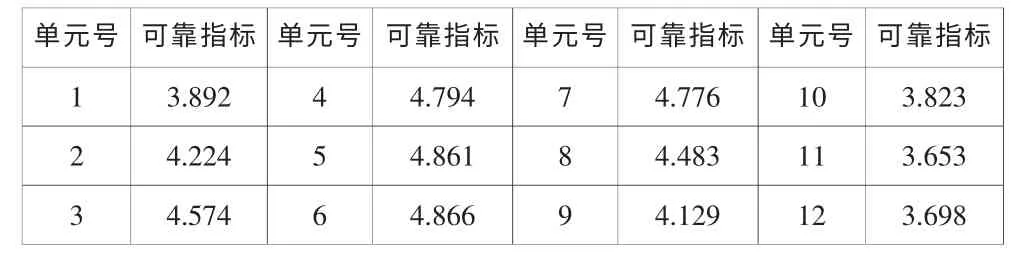
表3 混凝土襯砌單元的結構可靠指標

由表中的計算結果可以看出：隧洞頂部、底部單元的可靠指標較低，中部單元的可靠指標較高；隧道周邊單元的可靠指標均在3.6 以上，能滿足一般工程的要求。

5 結論

本文利用荷載結構原理和隨機有限元基本原理，建立了隧道可靠度的功能函數， 以某混凝土襯砌為例， 采用ANSYS 軟件進行編程計算，利用四節點等參隨機有限元法計算了該隧道襯砌單元抗拉強度的可靠指標。 計算結果表明，利用該方法計算隧道結構可靠指標是可行的。

［1］武清璽.結構可靠性分析及隨機有限元法[M].北京：機械工業出版社，2005.

［2］李權.ANSYS 在土木工程中的應用[M].北京：人民郵電出版社，2005.

［3］畢忠偉，丁德馨，饒龍.工程可靠度的隨機模擬次數[J].水利水運工程學報，2005（1）：44-46.

［4］畢忠偉，丁德馨，宋會蓮.地下工程可靠度的研究進展及趨勢[J].礦業開發與研究，2004（3）：27-30.