基于線路退運的靜態安全風險評估指標模型

李雋，趙一婕，吳軍，劉滌塵，董飛飛，潘旭東

(1.國網北京經濟技術研究院，北京市 100052;2.武漢大學電氣工程學院，武漢市 430072)

0 引言

電網的互聯發展使電力系統逐漸成為超大規模的系統，系統的運行情況更加不確定。在這種形勢下，自然災害或者嚴重故障的發生很可能破壞系統的安全穩定運行［1-3］，造成的后果包括線路過載和電壓越限等。分析電力系統的安全穩定狀態，采用基于風險的靜態安全評估方法對系統中的關鍵元件進行量化評估及排序，對于電力系統的規劃及運行方式安排均具有重要意義。電力系統的靜態安全風險評估［4-6］主要有3種方法，即確定性的評估方法、概率分析方法和風險評估方法。其中，確定性的評估方法沒有涉及系統的復雜性和隨機性;概率分析方法沒有考慮系統故障所造成的后果影響［7］;而風險評估方法同時考慮了故障發生的概率和故障所造成的后果，定量地反映了元件故障對系統的影響以及元件的重要程度。

本文將靜態安全風險評估指標及方法應用于輸電線路的重要性排序中，可以方便快捷地找出系統的關鍵環節，對尋求整個網絡連通性的關鍵線路以及評估網絡的安全性具有重要意義，同時可以為電力系統規劃人員進行系統的安全穩定性分析以及規劃建設提供技術支持和安全保障，并為電力系統運行人員進行系統在線監控及實時狀態評估提供參考和借鑒。

1 靜態安全風險評估原理

電力系統的靜態風險評估需要考慮事故發生的概率和事故產生的后果，可以用風險指標進行描述，相關概念的分析如下。

(1)發生事故的概率。經統計分析可知，系統發生的事故E符合泊松分布，即

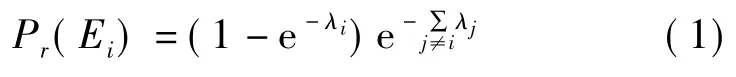
式中λi為在指定時間段內事故Ei發生的概率。

(2)事故產生的后果。為了描述系統的運行狀況，定義事故產生的后果為事故發生后系統狀態的概率與其嚴重度的乘積［8］。

造成系統狀態的不確定性因素主要有系統負荷及運行參數的不確定性。經統計可知，負荷的波動符合正態分布，系統的運行參數服從多元正態分布。經推導，系統的狀態 Yt服從正態分布［9］，即

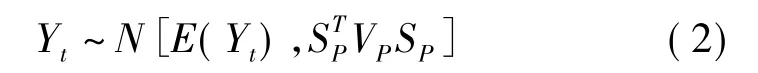
因此，由式(2)可以求得事故發生后系統狀態［10］的概率分布

系統風險的嚴重度可以用來定量描述事故造成后果的嚴重程度，可以用嚴重度函數來表示。嚴重度函數［11］是系統運行狀態Yt的函數，需要根據指定系統和風險類型來確定。嚴重度函數應根據指定系統、特定要求以及風險類型來建立。嚴重度考慮了事故發生后系統的經濟性和安全性，該方法能夠直觀反映系統的安全程度。

(3)電力系統風險。綜合以上分析，得到系統的靜態安全風險計算公式為

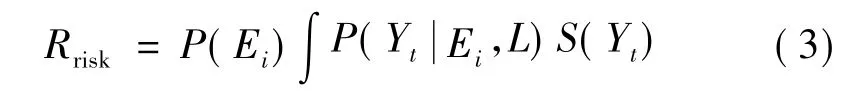
式中S(Yt)為系統處于Yt狀態時事故的嚴重程度。

2 風險指標的計算與重要性排序

2.1 線路的過負荷風險指標計算

(1)線路過負荷的嚴重度函數。事故發生后，其他線路的潮流分布決定了線路過負荷嚴重度的取值，其嚴重度函數如式(4)所示，曲線如圖1所示。由圖1可知，當輸電線路的有功功率小于或等于線路允許功率的90%時，其嚴重度取為0;當輸電線路的有功功率為線路允許功率的100%時，其過負荷風險嚴重度取為1，其中，設定線路功率額定值為定值。

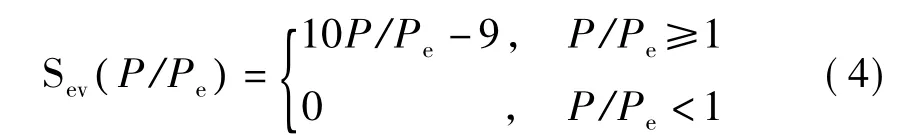
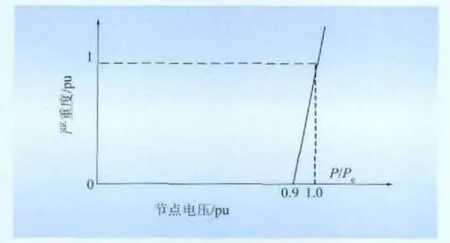
圖1 線路過負荷嚴重度函數Fig.1 Severity function of line overload

(2)過負荷風險指標。電力系統過負荷風險指標反映的是電力系統發生事故后，導致系統中未發生故障的輸電線路的有功功率超過其額定值的可能性和嚴重程度的綜合。將式(3)進行改寫，就能得到過負荷風險指標為

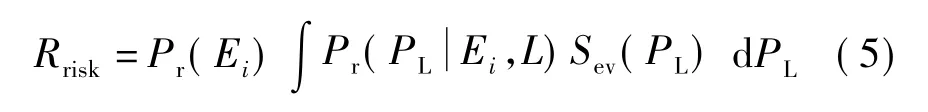
(3)過負荷風險指標的應用。應用上述過負荷風險的計算方法，計算出各條輸電線路的過負荷風險值，并對風險值進行降序排列。

線路的過負荷風險值越大，說明在發生自然災害或者嚴重故障時，這些線路的有功功率越容易超出最大傳輸功率，對整個電力系統的危害也越嚴重，因此，此類線路在規劃及實際運行當中需要進行重點關注。

2.2 電壓越限風險指標

電壓越限包含2個方面，即電壓越上限和電壓越下限，也就是過電壓和低電壓。一般情況下，采用繼電保護、避雷器等防御方式可以有效避免系統過電壓。而系統無功不足將引起低電壓問題，不但會使線路損耗增加，降低發電機的有功出力，而且可能燒毀電動機。因此本文主要集中于節點低壓風險領域。

(1)低電壓嚴重度函數。節點電壓的嚴重度取值取決于事故發生后節點的電壓，其嚴重度函數如式(6)所示，曲線如圖2所示。該曲線表示，當節點電壓為0.90時，節點低電壓風險的嚴重度函數為1.0;當節點電壓大于或等于1.0時，節點的低電壓風險嚴重度函數為0。

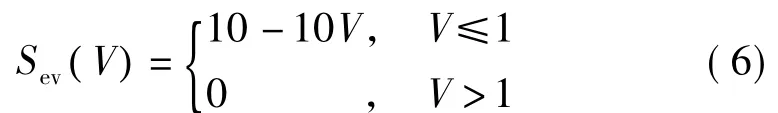
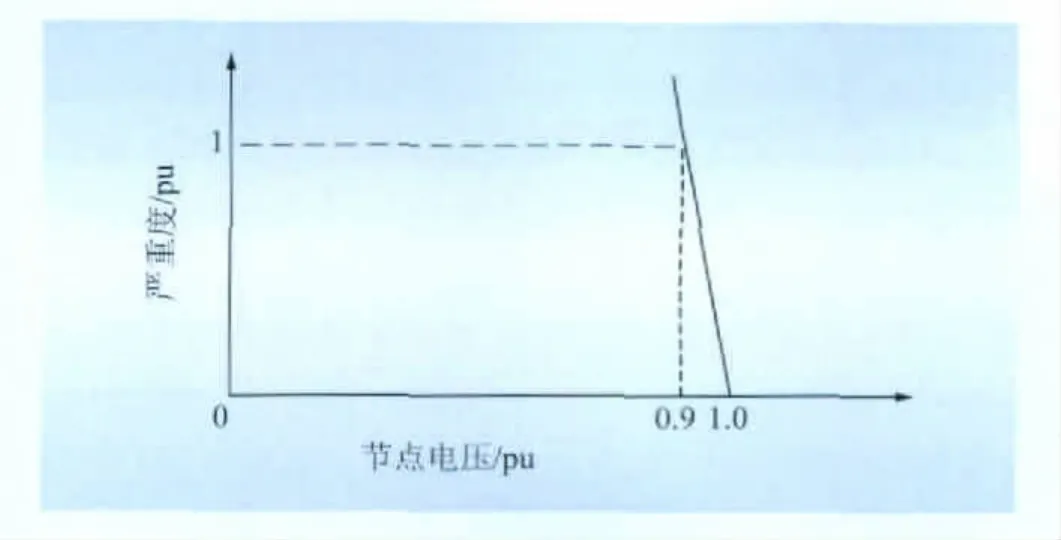
圖2 節點低壓嚴重度函數Fig.2 Severity function of node low voltage

(2)電壓越限風險。電力系統的電壓越限風險反映的是事故發生后導致電力系統中節點電壓超過其額定值的可能性和嚴重程度的綜合。將式(3)進行修改，得到電壓越限風險指標為

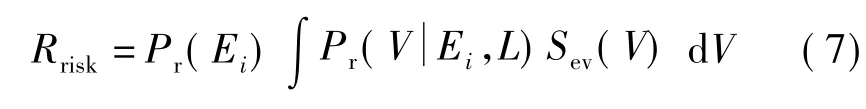
(3)電壓越限風險的應用。與過負荷風險的應用相似，可以對系統所有節點的電壓風險值進行降序排列。

電壓風險值越大的節點，表明在發生自然災害或者嚴重故障時，斷開此類線路之后將使其他節點出現電壓越限的風險提高，對整個電力系統造成更為嚴重的影響。

2.3 靜態安全風險指標的計算與評估

靜態安全風險指標的計算流程如圖3所示。依據計算流程，分別對相關指標進行計算，對不同線路斷開后系統的過負荷風險及節點電壓越限風險進行排序和比較，并將所有輸電線路按照正常運行功率、線路過負荷風險以及電壓越限風險進行重要性排序。

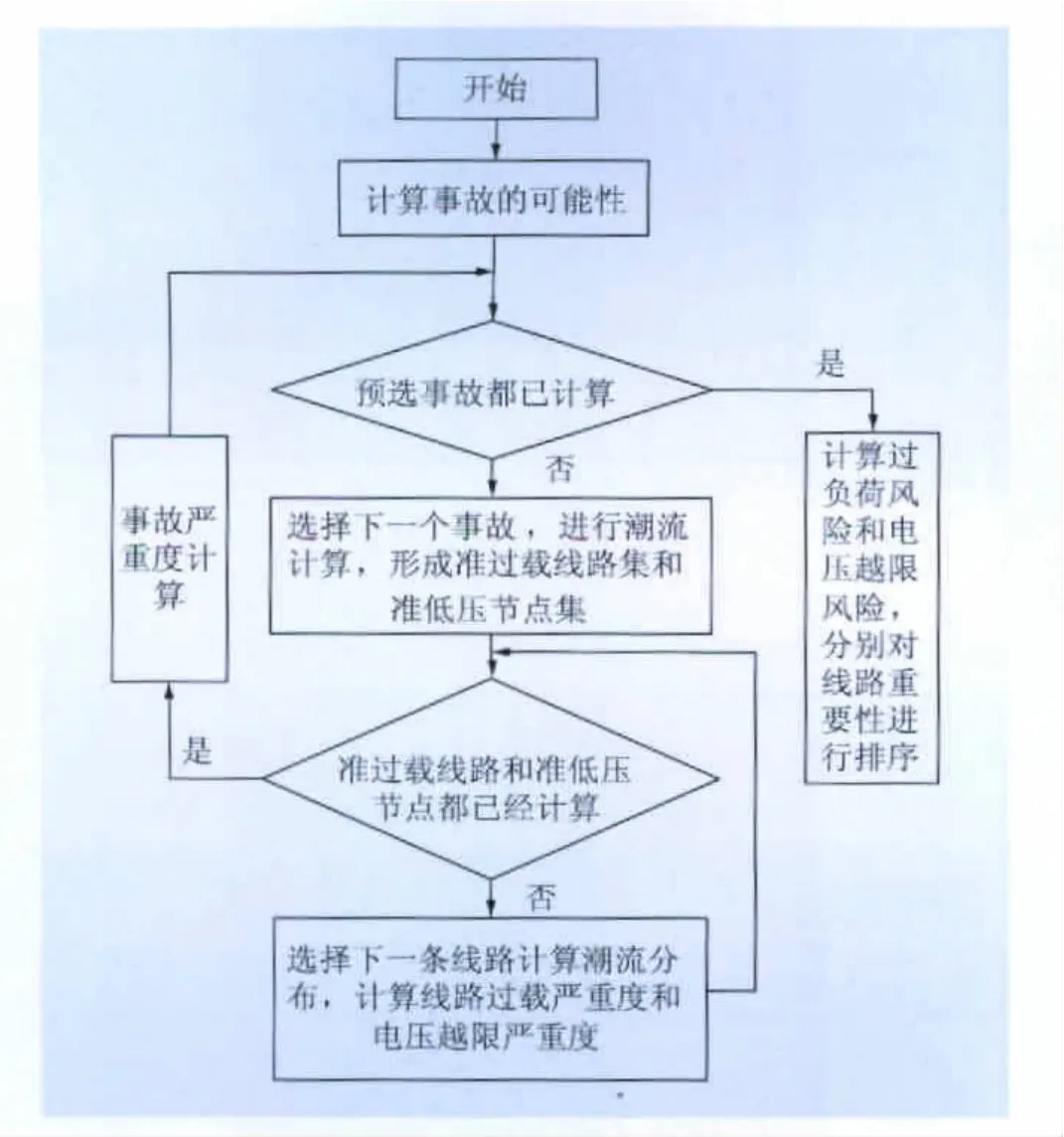
圖3 靜態安全風險計算流程Fig.3 Calculation flow of static security risk

3 計算實例

本文選用新英格蘭10機39節點系統，負荷分配因數的波動為5%，并以此作為系統運行參數的變化。設故障為單條線路無故障開斷，線路的年開斷率λy均為0.3，以事故 E，即開斷線路 L6為例進行計算。

3.1 過負荷風險計算及排序

當事故E發生時，通過潮流計算得到系統線路潮流與90%的最大傳輸功率如圖4所示。

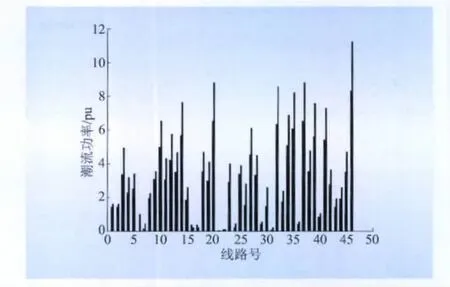
圖4 線路潮流與90%的最大傳輸功率Fig.4 Line power flow and 90%of the maximum transmission power

由圖4可知，線路L16、L17的潮流超過線路最大傳輸功率值的90%，需進一步分析。事故E的過負荷損失即為線路L16、L17的過負荷損失之和。同理可以得到發生其他事故時系統的過負荷風險。線路潮流與過負荷風險如圖5所示。

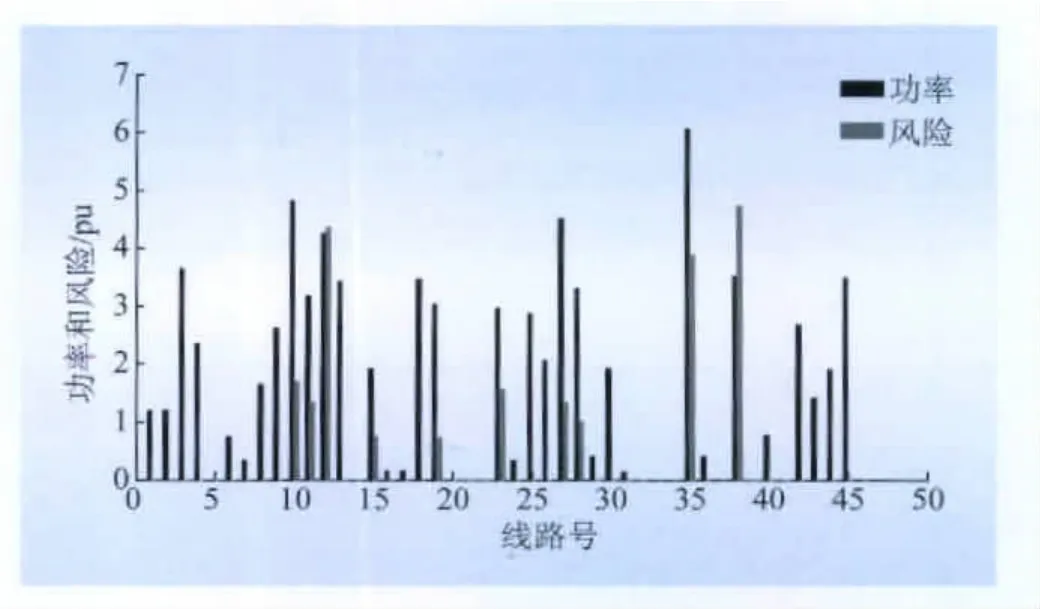
圖5 線路潮流與過負荷風險Fig.5 Line power flow and overload risk

3.2 電壓越限風險計算及排序

當事故E發生時，通過潮流計算得到系統節點電壓如圖6所示。

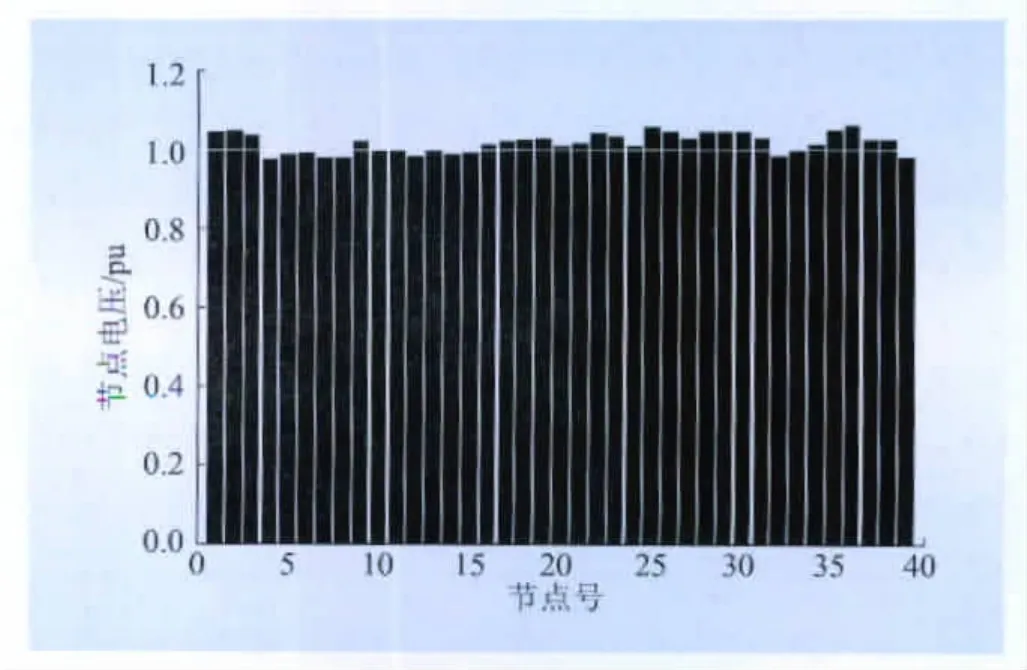
圖6 系統節點電壓Fig.6 System node voltage

由圖6 可知，節點 4、5、6、7、8、11、12、13、14、15、32、33、39的電壓幅值均低于正常電壓的門檻值1.0，需進一步分析。事故E1的電壓越限損失即為以上13個節點的電壓越限損失之和。同理可得發生其他事故時系統的低電壓風險如圖7所示。

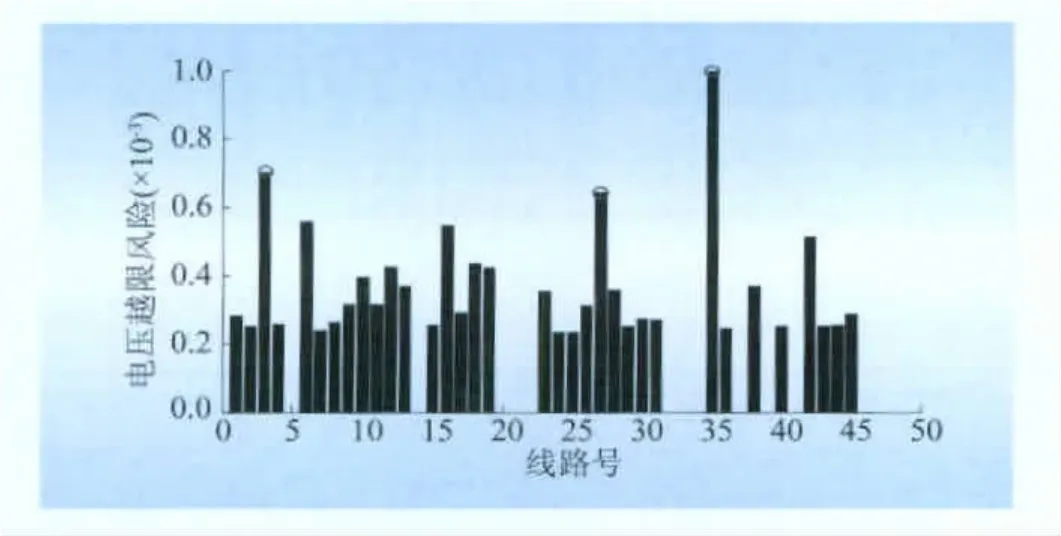
圖7 電壓越限風險Fig.7 Risk of voltage overlimit

3.3 結果分析

由圖5、7的結果可以分別對最重要的3條線路進行排序，如表1所示。

表1 3條線路排序Tab.1 Sequencing of three lines

依據初始線路的負載情況，可以得出3條線路分別為L35、L10和L27，依據線路過載風險指標進行排序得出最重要的3條線路分別為L38、L12和L35，依據電壓越限風險指標進行排序得出最重要的3條線路分別為L35、L3和 L27，可以看出3項指標結果并不相同，但是L35線路在3項指標中均比較重要。

4 結論

(1)線路在正常運行時的功率指標、線路斷線后造成的過負荷及電壓越限風險指標之間具有一定的聯系，但并非正常潮流功率越大的線路其過載及電壓越限的風險越大，主要原因是在靜態安全風險指標評估中，既考慮了風險的概率又考慮了風險的損失，只有概率及損失同時較大時，才會使風險最大，其最大風險指標所對應的線路在網架中的重要程度就越高，需要加強監視和維護。

(2)分別依據正常情況下的線路負載率、故障后的線路過載風險和電壓越限風險3項指標對輸電線路的重要性進行排序，線路的重要性排序不完全相同，這說明3種排序方法既相互依存，又相互獨立，任一指標的重要性并不能否定其他指標。

后續工作中將繼續完善靜態安全風險指標及其計算評估方法，并合并為多指標下的綜合靜態安全風險指標計算，對線路進行更加全面、科學的排序。

［1］侯慧.應對災變的電力安全風險評估與應急處置體系［D］.武漢:華中科技大學，2009.

［2］Chen W H，Jiang Q Y，Cao Y J.Risk assessment of cascading outages in power systems using fuzzy neural network［C］//Third International Symposium on Neural Networks，2006:1422-1427.

［3］Chen W H，Jiang Q Y，Cao Y J.Low voltage risk assessment in power system using neural network ensemble［C］//Third Internationa1 Symposium on Neural Networks，2006:1416-1421.

［4］陳曦，婁素華，吳耀武，等.電力系統靜態安全性評估綜述［J］.水電能源科學，2010，28(4):149-153.

［5］陳為化，江全元，曹一家.基于風險理論和模糊推理的電壓脆弱性評估［J］.中國電機工程學報，2005，25(24):20-25.

［6］王博.復雜電力系統安全風險及脆弱性評估方法研究［D］.武漢:華中科技大學，2011.

［7］肖盛.基于風險理論的電網脆弱性評估［D］.北京:華北電力大學，2011.

［8］陳為化，江全元，曹一家，等.基于風險理論的復雜電力系統脆弱性評估［J］.電網技術，2005，29(4):12-17.

［9］陳為化.基于風險的電力系統靜態安全分析與預防控制［D］.杭州:浙江大學，2007.

［10］鄒森.電力系統安全分析與控制［M］.北京:水利電力出版社，1995.

［11］王錫凡.現代電力系統分析［M］.北京:科學出版社，2003.