班車站點及路線的優化設計

馮存梅 李 威 沈 忱

（1.上海電機學院 電子信息學院，中國 上海201306；2.上海電機學院 機械學院，中國 上海201306）

0 研究背景

班車站點及線路的優化設計是屬于典型的車輛路徑問題（Vehicle Routing Problem,即VRP 問題）。VRP 問題在國外最早是由Dantzing 和Ramser[1]于1959 年首次提出的。早在1962 年，Balinski 等人就提出集分割[2]，直接考慮可行解集合并在此基礎上進行優化建立了最簡單的VRP 模型。1971 年，Eilon 等人[3]提出將動態規劃法用于固定車輛的VRP,通過遞歸方法求解。1991 年，Gendreau 等人[4]將禁忌搜索方法應用于VRP。M.L.Fisher 于1995 年 在 “Vehicle Routing Handbooks in Operations Research&Management Science”[5]中對車輛路徑問題作了總結，他把車輛路徑問題的研究方法歸結為三個階段。第一個階段，是20 世紀60 年代到70 年代，這個階段主要是應用一些簡單的啟發式方法來研究車輛路徑問題，研究的重點主要局限于局部搜索和交換技術；第二個階段，是20 世紀70 年代到80 年代基于啟發式方法的設計階段，這個階段主要是利用不同于一般啟發式方法的近似優化算法來求解車輛路徑問題。到了第三階段，即20 世紀80 年代至今，研究的重點主要放在精確的優化算法和新興的人工智能算法，包括模擬退火算法、禁忌搜索算法、遺傳算法和人工神經元網絡方法[6]。

在國內對VRP 研究最早的是郭耀煌教授，1989 年郭教授與其學生就多車場多車型等問題進行了研究[7]。1999 年姜大立等人[8]建立了VRP 的遺傳算法。2001 年，李嘉等人[9]設計了遺傳算法和禁忌搜索啟發式的混合算法。2004 年崔雪麗等人基于人工螞蟻系統給出了快速求解VRP 的螞蟻搜索算法。還有不少研究者均對VRP 的研究做出了很大的貢獻。單這些研究都是理論的東西，能夠更好的解決實際問題才能說明研究的價值。所以這些研究應該更偏向實際問題。

1 符號說明

M 企業或單位乘車總人數

L 總車輛數(k 表示第k 輛車)

Z 總站點數

N 總路徑數

C 每輛車的容量

Si第i 條路線

Pi第i 個站點

Yi第Si條路線的總乘客數

ωijk車輛k 從Pi站到Pj站的路程

Tijk車輛k 從Pi站到Pj站經歷的時間

2 班車站點設置的數學模型

設置站點的第一步是統計企業或單位的所有乘客的住址坐標（即住址所在的經緯度可利用google earth 標出）。記每位乘客的住址坐標為（ri，ci）（ri為經度ci為緯度）。假設共要設置站點Z 個,第j 個站點的坐標為（xj，yj）（xj為經度yj為緯度）。[10]

為使每位乘客到達站點距離的總路程最短及每位乘客到達站點的距離均衡以下給出總距離函數和最大距離與最小距離之差函數：

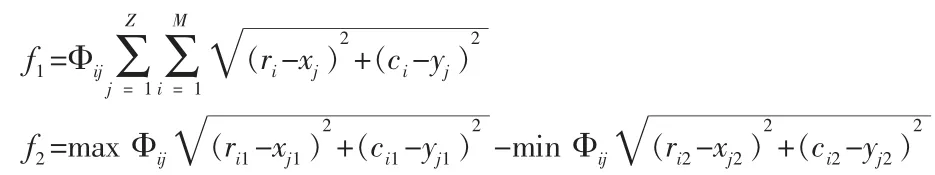
在設置站點的過程中還要考慮乘客到達站點所能承受的最大距離。假設乘客所能承受的最大距離為d1則有：

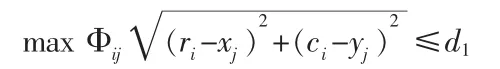
在衡量總距離與最大最小距離偏差時可在兩函數前加權重系數以更清楚地反映實際情況，綜合以上，可建立如下班車站點設置的數學模型：

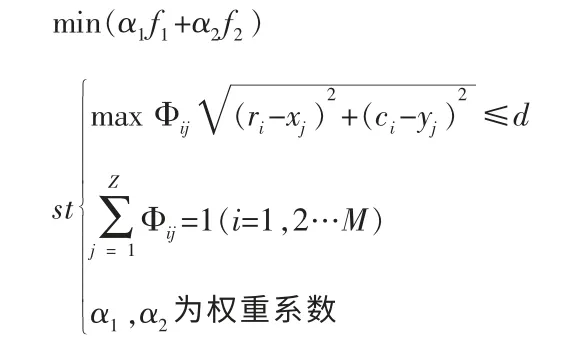
3 路線的優化設計

線路的設計優化模型建立過程中我們從多樣性角度出發并結合實際情況建立了兩種線路的模型。和多數研究者不同我們考慮了實際班車站點和路線在不同企業或單位中有些比較復雜但有些比較簡單，復雜的問題往往會有更多的目標和約束條件，解的過程也要復雜很多這是一種情況。在相對簡單的情況若仍按照復雜模型的思路和計算方法不僅得不到較好的結果還會浪費過多的時間和精力，是不經濟也是不實際的。因此我們建立了根據站點數量不同而路線安排也不同的兩種模型。即以下的模型一和模型二。

模型一：

此模型是針對一些乘客人數較少，站點較少或運輸資源有限等條件下建立的單一車輛單一路經的數學模型。僅僅適用于小型企業或單位，這種模型相對簡單但在實際應用中卻是經常要用到的。

在建立此模型中我們假設只有一輛車，車的容量足夠容納所有乘客。在站點已知且站點數目不是很多（說明：站點不多是指在總乘客數小于車容量下站點數一般小于20 個，此處20 只是對一般情況的假定，實際中具體個數應按實際需要設定）的情況下要求：①車要經過所有站點②車的路線最短③車輛行駛時間最短④除特殊情況外每個站點只經過一次（說明：特殊情況是指如不再次經過此站點車輛無法返回）。

從以上要求中可以看出此問題應屬于TSP （Travelling Salesman Problem）問題。此問題仍屬于NP-Complete 難題，許多學者在此問題上都花費了大量的精力但目前仍沒有徹底解決該問題的方法。這并不意味著此處是做無用功，在簡化數據和理想化一些條件后仍有一些有效的解決方法。

在上述要求中沒有提及成本問題，其實對于單一車輛單一路徑，車輛的成本是固定的。剩余的就只有運行的成本，運行的成本只與路程有關即只要求。

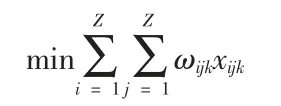
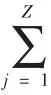
由以上要求可建立模型如下：

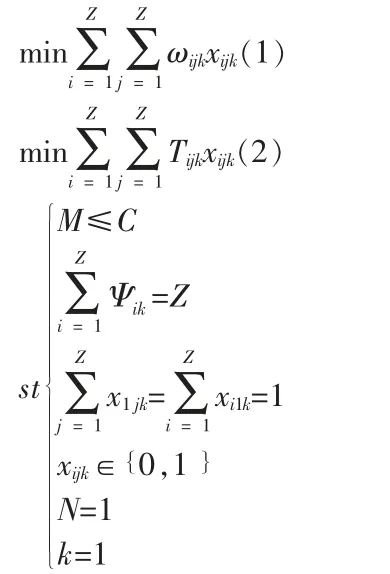
對目標函數（1）（2）其中（1）表示車輛行駛總路程最短（2）表示車輛行駛時間最短。對單一路徑來說當車速一定時，路程和時間是成正比的。但為什么此處既對路程進行約束又對時間進行約束在此說明一下。在下文中會涉及道路飽和度的因素當滿足（1）時在某些情況下會因為道路達到飽和而使運行時間過長，此時就會受到（2）的約束改變路線即使行駛路程增加但行駛的時間卻比原先減少了，這樣更有利于車輛運行效率，也更符合實際情況。第一個約束條件表示乘客總數不大于車的容量。第二個約束條件表示車必須經過每一個站點。第三個約束條件表示車從1 站點出發必須回到1 站點（假設1 站點為目的地）。第四個約束條件表示變量x 的0-1 約束。第七第八約束條件分別表示只有一條路徑和只有一輛車。

模型二：

此模型較模型一要復雜，是更具有廣泛性和實用性的一般性模型。模型二是針對多人員多站點多線路多種因素綜合考慮建立的。因為是一般性模型所以模型二較模型一相比具有多條線路，多車輛。在設置好站點后我們先用floyd 算法求出所有站點之間的最短路，由最短路依次從距原點最遠，第二遠…第N 遠為起點設置N 條線路，設置線路按兩條原則一是盡量走最短路二是所有線路盡量囊括所有站點對有些特殊情況則另作分析。具體方法見模型算法設計。

在多條路線中車輛數既不能少于總需求量也不能過多，車輛數是決定成本的重要因素所以目標函數首先應滿足使總車輛數達到最少。即：

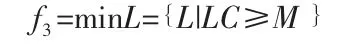
車輛達到最少是首先決定因素其次是使所有車輛行駛總路程最短，因為除車輛的固定成本外路程所決定的運行成本從長期來看也是重要的因素。即：

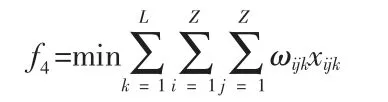
同樣在保證總路程最短的前一約束下還要使時間達到最小化。設定時間的約束原因如模型一中設定時間約束的一樣，同樣是因為道路飽和度的考慮，其約束如下：

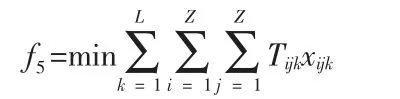
在所有路線中為出于對乘客滿意度和公平性的考慮應使最長路線與最短路線的差值在一定的可接受范圍內，假定最大差值為d2則有：

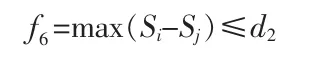
綜合以上模型可建立如下：

min（α2f2＋α3f3＋α4f4＋α5f5）

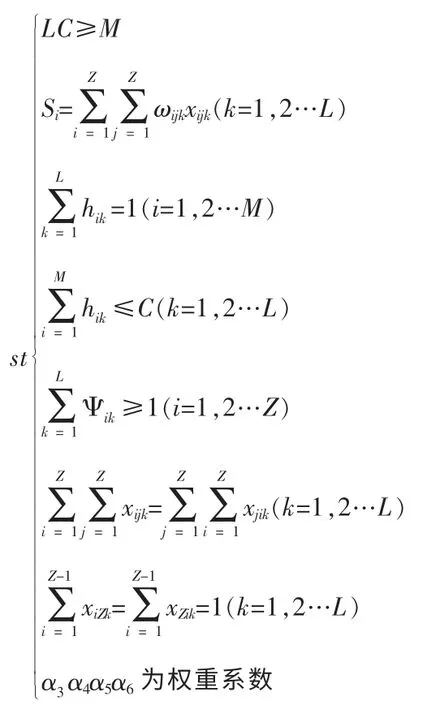
以上模型中目標函數的意義在上文中已說明此處說明一下約束條件的意義：約束條件一表示運載能力的限制即最大運載量要大于總人數。約束條件二表示每條路線的距離。約束條件三表示任意一位乘客只能乘坐一輛車。約束條件四表示每輛車的載客量不超過車的容量。約束條件五表示任意站點至少有一輛車經過。約束條件六表示同一輛車可以從pi站到pj站也可以從pj站到pi站即下行方向為上行方向的反向。約束條件七表示上行方向各路線的目的地為終點站下行方向各路線的發車點為終點站（假設第Z 站為終點站）。

4 道路飽和度的考慮

此處道路飽和度并沒有用符號在模型中表示出來是出于對模型求解可行性的考慮，因為就算沒有考慮道路飽和度此模型的求解也相當困難。但是道路飽和度是實際問題中不得不考慮的一項因素，特別是在大城市的上下班高峰期，往往會因為交通堵塞浪費大量時間這是很不合理的。此處對道路飽和度的考慮，實際上也是對路線的修正因為在有些已達到飽和的道路再安排車輛通行就不滿足時間的約束，就需要對線路進行調整。因為道路什么時候達到飽和往往與時間有關，這就要根據對不同環境的實際經驗來判定。當道路達到飽和時即通行時間遠超正常通行的時間，就在此時刻對此線路采用繞道而行的調整方案。

例如車輛k 在某時刻t 從pi站到pj站，在時刻t 此時道路ωijk達到飽和。則車輛k 在pi站與pj站途中繞經pα站，若滿足Tiαk＋Tαjk＜Tijk原來的路徑就改為車輛K 從pi站到pα站再到pj站。這樣雖然多走了一些路程但卻節省了一部分時間從效率角度講這樣做是合理的。

但對時刻t 模型和算法中是無法給出的，因為其一t 的數值無法確定其二t 具有不穩定性即每天情況可能不一樣，只有根據實際經驗才能確定。模型算法最終給出的結果只要根據實際經驗來作調整即可，所以此處只做說明。

5 站點設置的算法設計

因為對不同的案例站點的設置千變萬化，無法給出一個能保證最優最精確的解，所以站點設置算法我們采用一般情況下的啟發式算法。如上文所描述模型思想按照算法步驟在一般情況下均可得到較滿意的結果。

（1）輸入：乘客到達站點所能承受的最大距離d1以及距離函數與距離偏差函數的權重系數α1，α2；

（2）在地圖上標注出每一位乘客的住址（ri，ci）（實際操作可用google earth 由經緯度標注出）；

（3）在地圖上建立合理的坐標系將乘客住址的經緯度轉換成坐標系中的實際坐標；

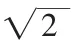
（5）統計出總的區域個數Z 和每個區域的住址點數及乘客數M；

（6）計算出每個圓或矩形的中心（此中心為該區域總路程最短的中心或住址點的重心），并將這些點的坐標作為站點的地理位置；

（7）輸出：所有的站點位置的坐標及每個站點的人數。

6 路線模型一的算法設計

對于路線一可看做是簡化的TSP 問題,在圖論中有類似像哈密爾頓圖以及二次逐次修正法這樣解決行遍性問題的一般方法。哈密爾頓圖的定義：設G＝（V，E）是連通無向圖，經過G 的每個頂點正好一次的路徑稱為G 的一條哈密爾頓路徑，經過G 的每個頂點正好一次的圈稱為G 的哈密爾頓圈或H 圈，含H 圈的圖稱為哈密爾頓圖或H 圖。[11]

在推銷員問題中經過每個頂點至少一次權最小的閉通路稱為最佳推銷員回路。一般來說最佳哈密爾頓圈不一定是最佳推銷員回路，最佳推銷員回路也不一定是最佳哈密爾頓圈。像模型一這樣求單車路程最短不適合用求哈密爾頓圖的方法，而二次逐次修正法雖然是近似解法卻往往能給出滿意的結果。但二次逐次修正法的前提是要求所解圖必須是完備圖，對于車輛站點路線來說很少有滿足此要求的路線圖。這里我們對于不滿足條件的圖用替代的方法構造成完備圖。即用最短路代替沒有相鄰的點之間的路徑。具體算法如下：

1）標記所有站點（v1v2…vi…vj…vn）并計算出所有連通站點之間的距離，做出站點路線圖的帶權鄰接矩陣W。

2）由鄰接矩陣W 應用Floyd 算法計算出此站點路線圖的最短路。

3）任取初始H 圈：C0＝v1v2…vi…vj…vnv1。

4）由于任取的初始H 圈中有些排列相鄰的站點之間在實際中并不直接相鄰，所以對這些站點之間的權值由（2）中所求最短路代替。

5）對所有i，j，1＜i＋j＜n 若W（vi，vj）＋W（vi＋1vj＋1）＜W（vivi＋1）＋W（vjvj＋1）則在C0中刪去邊（vivi＋1）和（vjvj＋1）加 入邊（vi，vj）和（vi＋1vj＋1），形成新的圈C，即：C＝v1v2…vivjvj－1…vi＋1vj＋1…vnv1。

6）對C 重復步驟⑷直到條件不滿足為止，最后求得的C 即為最佳H 圈。

7）將所求H 圈中站點序列從發車站依次記錄最終所得站點序列的路徑即為模型一的車輛路徑。

7 路線模型二的算法設計

模型二是屬于多線路的一般性模型，對于此類模型的求解大部分研究者都用了像遺傳算法，啟發式算法，蟻群算法，動態優化法等算法。本文也不例外采用了啟發式算法，因為這個模型本身就比較復雜再由于實際情況的各種變化，很難給出能解出穩定結果的算法。啟發式算法雖然不一定能給出準確結果，卻能根據實際經驗在復雜的環境中給出讓人較為滿意的結果。其算法過程具有可調節性，在不同條件下很容易根據實際情況調整，使其更切合實際。具體算法如下：

1）輸入：最長路線與最短路線的差值的極限值d2，客車容量C，各個站點的坐標位置和各站點人數。

3）由Floyd 算法根據個站點路線圖計算出最短路。

4）在最短路中取距終點最遠的L 個站點，根據距終點的距離由大到小分別計為線路S1S2…SL的起始站點。

5）從S1開始按最短路到終點確定第一條路線，依次確定L 條路線。

6）調整從S2到SL的L－1 條路線，調整的原則為：①將未在路線中的站點調整至路線中；②站點調整時只將此站點納入據此站點最近的路線中；③調整過程中路線以走最短路為優先原則。若所有未在路線上的站點均調整在了路線中則轉（7）。

7）在所有站點均考慮的前提下，計算出每條路線的路程分別計為S1到SL的實際值，若max（Si－Sj）＞d2則轉至（6）重新調整路線直至max（Si－Sj）≤d2則轉至（8）。

8）計算每條路線上總乘客數，有多條路線經過同一站點時只將此站點計算至其中一條路線。若Yi＞C 則將Si中Yi－C 個乘客交換到其他路線（以有重合站點的一對路線為優先原則進行交換）。直至對所有路線均有Yi≤C。

9）輸出：S1至SL中L 條路線的站點路線以及每條路線所包含的站點，每個站點的上車人數在不同路線的分配。

［1］Dantzig, Ramser. The truck dispatching Problem, MgtSci[M]. 1959, 6: 81-85.

［2］Balinski M, Quand R. On an integer program for a delivery problem [J].Operations Research, 1962,12: 300-304.

［3］Eilon S, Watson -Gandy C DT, Christofides N. distribution management:mathematical modeling and practical analysis [M].London: Griffin, 1971.

［4］Gendreau M, Hertz A, LaporteG A. tabu search heuristic for the vehicle routingproblem[M]. Montreal: Publication#777, Centre de recherchesur lestranspors,1991.

［5］M.L.Fisher.Vehicle Routing Handbooks in Operations Research & Management Science. Vol8, 1995[S].

［6］金燕波.校車路徑優化問題研究[D].吉林大學,2006.

［7］郭耀煌.安排城市卡車行車路線的一種新算法[J].統工程學報,1989,4(2)70-78.

［8］姜大立,等.車輛路徑問題的遺傳算法研究[J].系統工程理論與實踐,1999(6):40-45.

［9］李嘉,等.一類特殊車輛路徑問題(VRP)[J].東北大學學報:自然科學版,2001,22(3):245-248.

［10］張富朱泰英.校車站點及線路的優化設計[J].數學的實踐與認識,2012-02-23.

［11］Herbert Fleischner.歐拉圖與相關專題[M].科學出版社,2012-04.