一道平面幾何題的六種證法
和玉梅
(麗江師范高等專科學校,云南麗江674100)
平面幾何是中學數學的基本內容之一。 平面幾何題千變萬化,證法靈活多樣,一題可有多種證法。 在平時的教學中,通過一題多證,可以加深學生對各學科知識的系統理解, 培養學生的邏輯推理能力,進一步拓展學生的思維水平;使他們能熟練、系統地運用掌握的基礎知識去分析問題和解決問題,更重要的是提高和培養了學生綜合解題能力和思維能力。下面以一道經典平面幾何題為例,作六種證法和總結。
1 題目
題目:如圖1,已知AD∥BC,∠1=∠2,∠3=∠4,
直線DC 過E 點交AD 于D,交BC 于C。
求證:AD+BC=AB
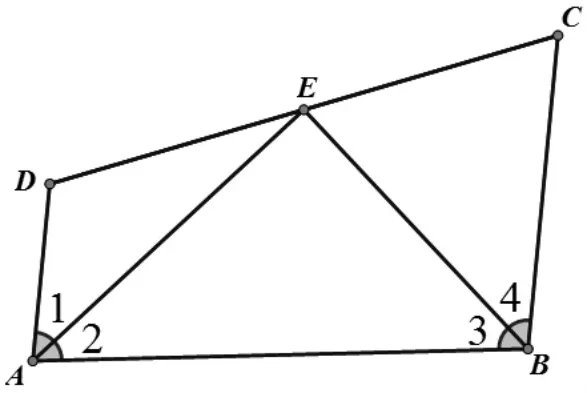
圖1
2 證法
證法一:【分析】如圖2,在AB 上截取AF,使AF=AD,再證FB=BC即可,此為截長法。
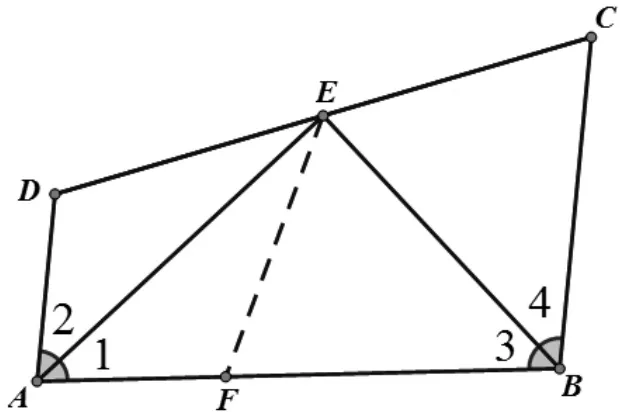
圖2
【證明】如圖2,在AB 上截取AF,使AF=AD
在△ADE 和△AFE 中,
∵AD=AF,∠1=∠2,AE=AE
∴△ADE≌△AFE
∴∠ADE=∠AFE
∵AD∥BC,∴∠ADE+∠ECB=180°
又∵∠AFE+∠EFB=180°,∴∠EFB=∠ECB
在△BEF 和△BEC 中,
∠3=∠4,∠EFB=∠ECB BE=BE
∴ △BEF≌△BEC,∴BC=BF
因此,AD+BC=AF+BF=AB
即:AD+BC=AB
證法二:【分析】如圖2,作∠AEF 使∠AEF=∠DEA,EF 交于F
則AF=AD,再證FB=BC 即可
證明:作∠AEF 使∠AEF=∠DEA,EF 交于F
在△ADE 和△AFE 中,
∵∠AEF=∠DEA,∠1=∠2,AE=AE
∴△ADE≌△AFE
∴∠ADE=∠AFE
∵AD∥BC,∴∠ADE+∠ECB=180°
又∵∠AFE+∠EFB=180°,∴∠EFB=∠ECB
在△BEF 和△BEC 中,
∠3=∠4,∠EFB=∠ECB BE=BE
∴△BEF≌△BEC,∴BC=BF
因此,AD+BC=AF+BF=AB
即:AD+BC=AB
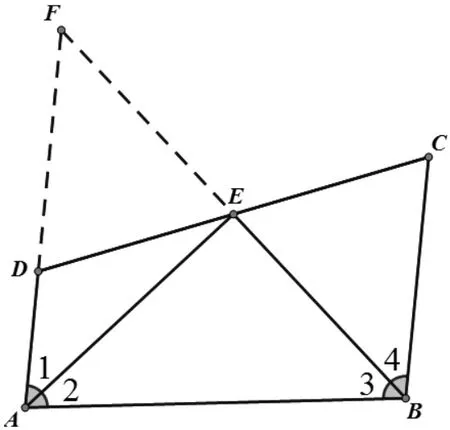
圖3
證法三:【分析】由AD∥BC,∠1=∠2,∠3=∠4 得
∠BAE=90° AE⊥BE。
可延長AD、BE 交于點F
再證DF=BC,此為補短法。
【證明】延長AD、BE 交于點F
∵AD∥BC,∠1=∠2,∠3=∠4
可得,∠BAE=90°,AE⊥BE
∴Rt△BAE≌Rt△FAE,
∴AB=AF、BE=EF
從而可證,△FDE≌△BEC
DF=BC
∴AB=AF=AD+DF=AD+BC
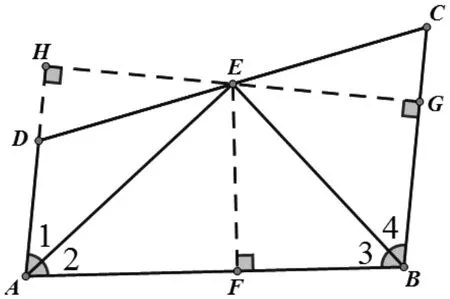
圖4
證法四:【分析】如圖4,因點E 是∠DAB 和∠CBA 的平分線的交
過E 點作EF⊥AB 交AB 于F、EG⊥BC 交BC 于G、EH⊥AD 交AD 的延長線于H,則EF=EG=EH
從而,S△EDA+S△EBC=S△EAB, 利用三角形面積公式再證AD+BC=AB即可,此為面積法。
【證明】過E 點作EF⊥AB 交AB 于F、EG⊥BC 交BC 于G,EH⊥AD 交的延長線于H,
∵∠1=∠2,∠3=∠4
∴EF=EG=EH
從而,Rt△EHA≌Rt△EFA
Rt△EFB≌Rt△EGB
Rt△EHD≌Rt△EGC
∴S△EDA+S△EBC=S△EAB
∵EF=EG=EH
∴AD+BC=AB
證法五:【分析】由AD∥BC,∠1=∠2,∠3=∠4,得
即可證得AD+BC=AB ,此為等量代換法。
【證明】取AB 的中點,連接EF
∵AD∥BC,∠1=∠2,∠3=∠4
∴∠1+∠3=90°
∴△EAB 是Rt△
∴EF=AF=BF=1 2 AB
從而,∠1=∠2=∠5
∠3=∠4=∠6
∴AD∥EF∥BC
∴EF 是梯形ABCD 的中位線,
∴AD+BC=AB
證法五:【分析】如圖5,過點E 作EF∥AD∥BC 交AB 于點F,則
∠AEF=∠1=∠2,故EF=AF,同理EF=BF
從而,EF 是梯形ABCD 的中位線,從而,EF=1 2 (AD+BC)
又由由AD∥BC,∠1=∠2,∠3=∠4 得
即可證得AD+BC=AB ,此為等量代換法。
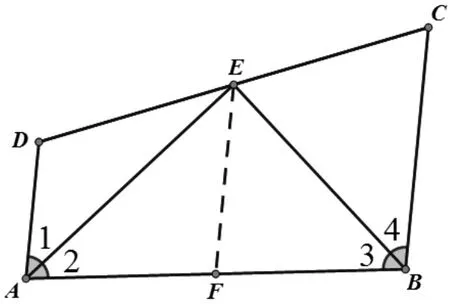
圖5
【證明】過點E 作EF∥AD∥BC 交AB 于點F,
則∠AEF=∠2,又因為∠1=∠2,
∴EF=AF,同理可證EF=BF
∵AD∥BC,∠1=∠2,∠3=∠4
∴∠1+∠3=90°
∴△EAB 是Rt△
∴AD+BC=AB
通過本例,挖掘了“截長或補短法”、“面積法”“等量代換法”等解決平面幾何問題的四種數學思想和方法,這也是平面幾何中解決線段間關系問題最常用的幾種方法。
[1]雷君,畢曉欣.三點一測叢書[M].科學出版社,龍門書局,1998.

