階梯電價政策對居民用電的影響分析：以上海市為例

●武漢大學經濟與管理學院 趙 昕

引言

從2009年底開始，各地方政府陸續開始對階梯電價進行聽證。階梯電價也繼而成為人們關注的焦點。截至2012年8月7日，全國29個試行居民階梯電價的省區市均已對外公布執行方案，九成提高了首檔電量標準，居民用電成為大眾關注的焦點。那么提價的合理性如何，能否保證大多數居民用電不受影響以及對于二、三檔電用戶支出影響情況等都成為研究的重點。本文以上海市為例，對上述問題進行了分析。

一、文獻回顧

劉樹杰、楊娟(2010)在《關于階梯電價的研究》中論證了階梯電價的合理性，并在此基礎上提出了我國階梯電價的設計方案和路徑。朱柯丁、宋藝航、譚忠富等(2011)在《居民生活階梯電價設計優化模型》中建立了階梯電價實施方案優化模型。利用秩和比法確定地區最適合的階梯分檔次數等方面。 曾鳴、李娜、劉超(2011)在《基于效用函數的居民階梯電價方案的節電效果評估》中建立居民階梯電價方案的評估模型，用來評估不同階梯電價方案所帶來的節電效果。

本文的創新點在于，借助正態分布函數與Lorenz曲線方程的關系，求出了Lorenz曲線方程的表達形式。將描述收入與財富分配的該曲線轉化為用來描述居民用電量與居民比例關系的曲線，從而反映了居民用電分配的不平衡程度。其次，通過Lorenz曲線方程求出了為滿足80%的居民用電支出不受影響的一檔電上限。在此基礎上，建立了居民支出函數、支出增長比例函數等，求得了每檔電，居民的平均支出增加情況。

二、居民用電量分布與Lorenz曲線

本文以上海市某年平均用電量的小樣本抽查數據作為樣本進行分析。以估計到的參數作為參照。在此基礎上，以當前居民用電量分配的情況，即大約5%的高收入家庭消耗了24%左右的居民用電,10%的高收入家庭消耗33%的居民用電，作為新的數據來源，建立Lorenz曲線方程，進行參數矯正。

（一）上海市居民年平均用電量抽樣

圖1 上海市部分居民戶年平均用電量直方圖

數據的參數估計。本次抽樣共獲得10000組數據，為10000戶家庭的年平均用電量。其分布直方圖如圖1所示。

由圖1可以看出，用電量分布基本符合正態分布。為進一步驗證用電量符合正態分布的合理性，用matlab軟件，借助Jarque-Bera test以及Lilliefors test檢驗其是否服從正態分布。結果顯示，在95%的置信區間內，都要否定原假設，即可認為這組數據符合正態分布。用matlab進行正態分布的擬合，得到其均值為173.29，方差為51.317。

（二）用電量分布函數與Lorenz曲線

1.用電量分布函數。居民用電量的分布服從正態分布，其密度函數為：

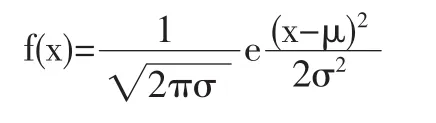
其中x表示居民年平均用電量。

其累積分布函數為：

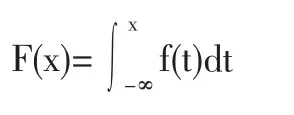
其含義為：用電量不超過x的用戶占總用戶的比例，或用電量不超過x發生的概率。

2.Lorenz曲線。Lorenz曲線是指在一個總體（國家、地區）內，以“最貧窮的人口計算起一直到最富有人口”的人口百分比對應各個人口百分比的收入百分比的點組成的曲線。它也是累積分布函數的一種描述形式，與累積分布函數存在對應關系。

具體關系如下面公式所示：

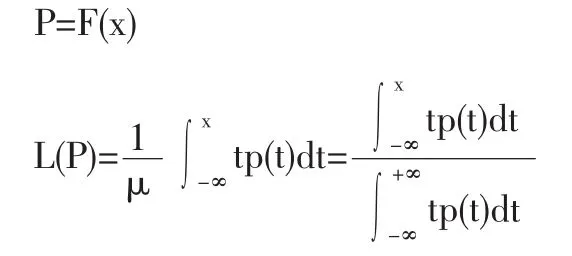
即最低收入P%的居民擁有總收入L%的財富,將人口百分比放在橫軸、收入百分比放在縱軸所得到的圖形。

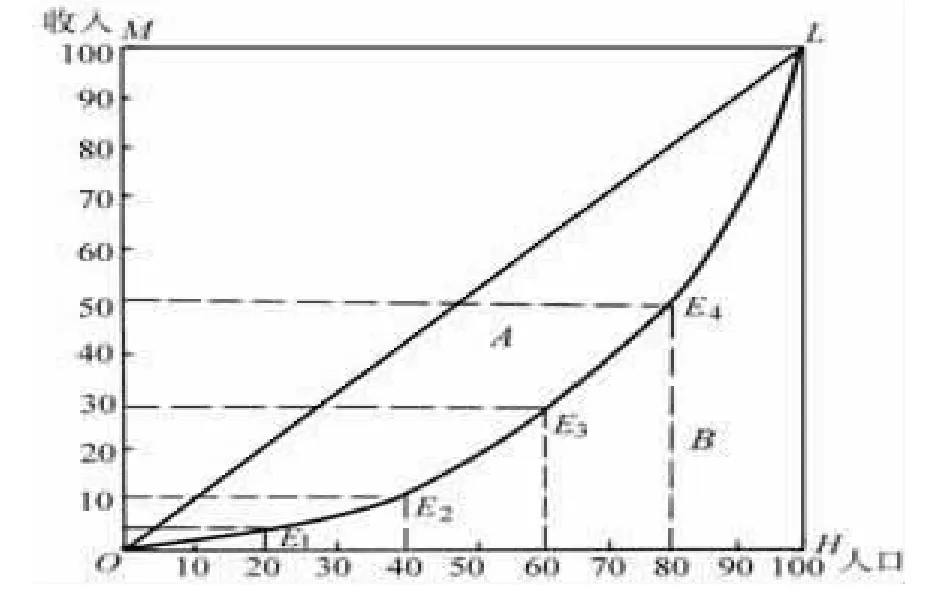
圖2 Lorenz曲線

（三）基于Lorenz曲線的參數估計。將收入類比于居民用

電量，可以得到居民用電量的Lorenz的曲線。根據居民用電分配基本情況的兩組數據（0.05,0.24），（0.1,0.33）列出的相應方程為：

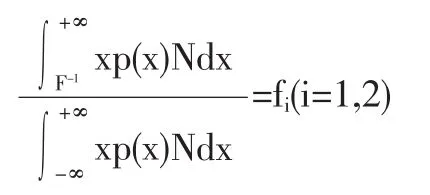
其中，1-αi=0.05,0.1 且 1-fi=0.76,0.67。

使用數值分析的方法，并基于已擬合的均值173，設置均值范圍為（100,200），可以求得調整后的均值為179。Lorenz曲線的圖形為：

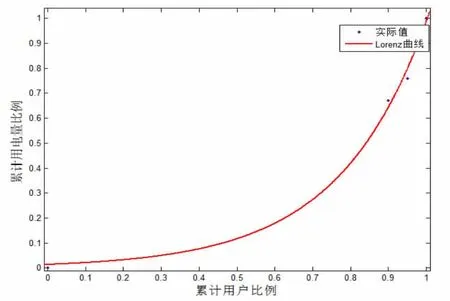
圖3 用戶年均用電量的Lorenz曲線

Lorenz曲線反映了用戶用電分配的狀況。曲線上的某一點A(a%,b%)表示百分之a的用戶使用了全部百分之b的電量。

三、多數上海市居民電費支出平穩性分析

本文中，居民用電的平穩性是指能否保證民生穩定，即能否保證80%的低電量消費戶的用電支出不受影響。

上海市的三檔電調價政策如表1：

表1 上海市三檔電

保證80%的居民用電支出不變，即要求一檔電的上界260對應的概率不小于80%。表現在累計分布函數上為，當x為260時，對應的F(x)值應不小于80%。用matlab求解，可以得到當x為260時，F(x)值為0.62，小于80%，故調價政策無法保證80%的居民用電不受影響。

那么為保障80%居民用電支出不受影響，現有一檔電調價政策應做部分改進。可以算出當F(x)值為80%時，x為396.98度，即一檔電的上限為396.98度。相應的二檔電的上限亦應做出調整，此處暫不作考慮。

四、上海市居民用電量不平等測度

居民用電量的不平等測度包括很多方面，本文的測度指標為Lorenz曲線對應的FGT指數以及Gini系數。

（一）基于FGT指標的居民用電量稀缺程度評價。FGT指數有離散型和連續型兩種，連續形式的FGT指數是建立在用電量累積分布函數之上的，可以表示為：

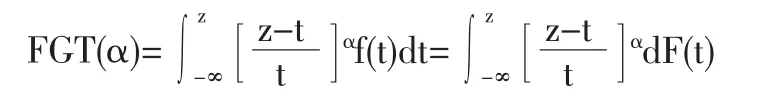
式中，z為給定的用電量的低檔線，系數α用來測算不同用電量階層對指數值的敏感性，α取值越大時，用電量較少的用戶的用電量對指數取值影響越大。

帶入累積分布函數，可以算出：

當α=0時，FGT(0)=0.62276，表示一檔電覆蓋的廣度為62%的低用電量人群。

當α=1時，FGT(1)=0.57246，表示一檔電覆蓋的人群提高用電量的松弛度為57%。

（二）基于Gini系數的居民用電量分配不平等評價。Gini系數是Lorenz曲線所定義的判斷收入分配公平程度的指標。其為比例數值，取值在0和1之間。Gini系數與Lorenz曲線的關系可以表示為：

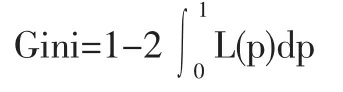
求解得：Gini等于0.223，圖形表示為：

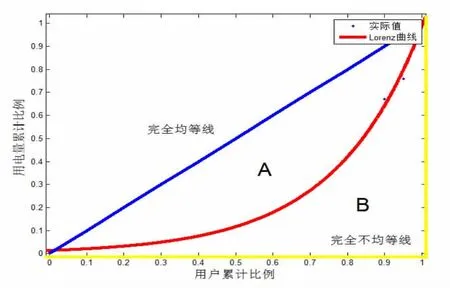
圖4 用電量的Lorenz曲線的詳細描述

Gini系數用圖中的面積表示為：

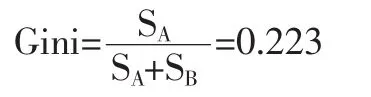
根據聯合國的有關組織規定：Gini系數若低于0.2表示收入絕對平均；0.2-0.3表示比較平均；0.3-0.4表示相對合理；0.4-0.5表示收入差距大；0.6以上表示收入差距懸殊。此處求得的Gini系數為0.223，從用電量的角度可以理解為：用電量比較平均，即用電量的變動幅度不大。

五、階梯電價對居民用電支出的影響

階梯電價對居民用電支出的影響可以分為三類，分別是對三檔電用戶的影響。其中，一檔電電價不變，其用戶不受影響；二、三檔電電價提高，對用戶支出存在一定影響。用戶電費支出可以表示為

其中，C 表示年平均用電支出，p1、p2、p3表示一、二、三檔電的價格。x1表示一檔電上界，x2表示二檔電上界。x表示用電量。用電支出圖為：

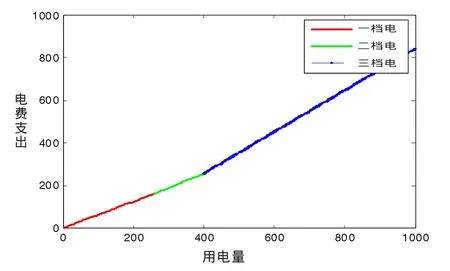
圖5 階梯電價居民用電支出情況

從圖中可以看出，居民的用電量在進入更高一檔電時，電費支出的斜率相應增加，邊際支出更大。因電價上調導致的支出增加百分比為：

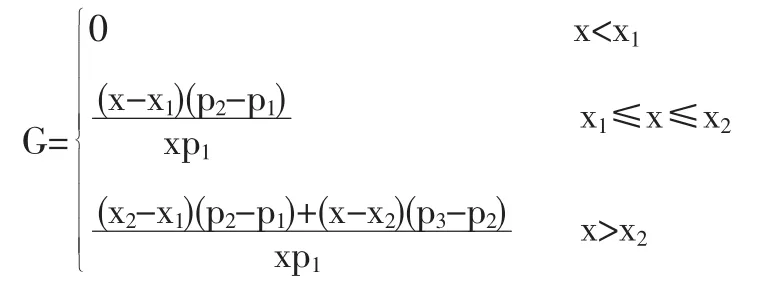
支出增加百分比的圖為

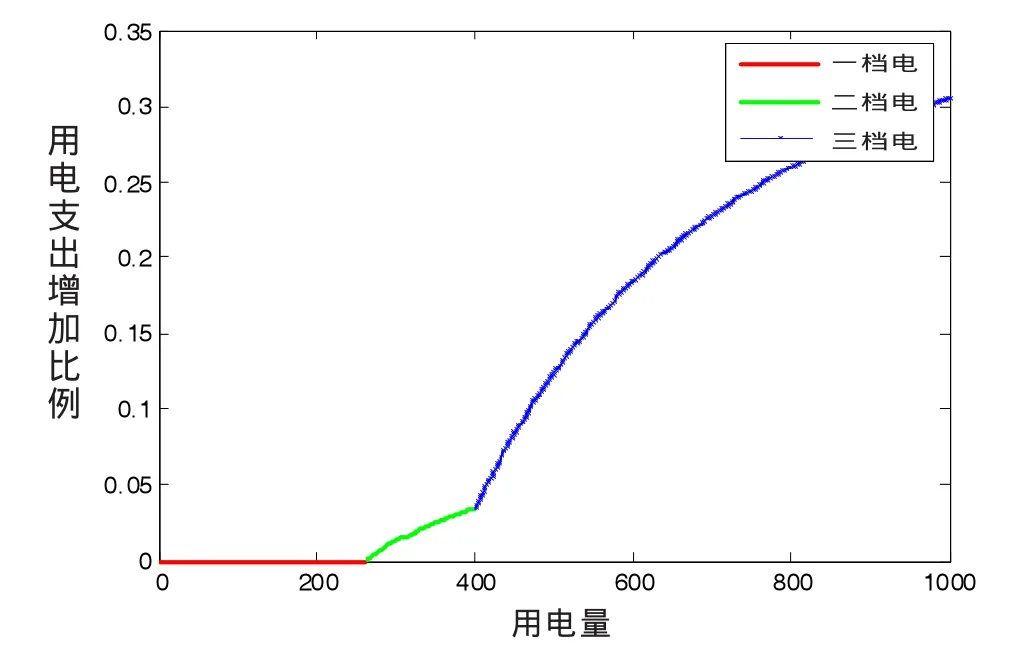
圖6 居民用電支出增加比例

從圖中可以看出，除一檔電用電支出不受影響外，其他檔電費支出隨用電量增加而增加，但增加幅度逐漸減小，即電費支出增加的速度逐漸減小。

對于每一檔電，用戶平均支出增加百分比期望為：

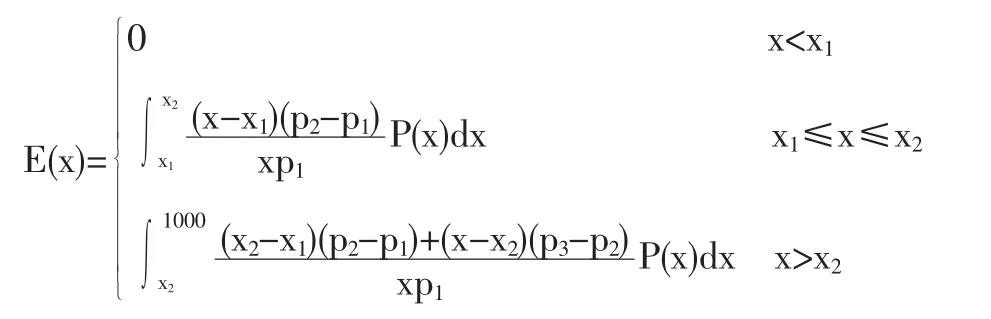
其中，假設三檔電用戶的用電上限為1000度。

計算得，二檔電用戶平均支出增長0.7%，為1.25元。三檔電用戶平均支出增長3.6%，為9.12元。可見對于三檔電用戶每度電增加0.3元，造成的支出增加更大，更明顯。

六、政策建議

其一，在保證用電成本完全彌補的情況下，提高一檔電的上限，對低收入家庭提供部分免費電。根據上文中得到的結論，一檔電的上限有待提高。以現在的用電劃分標準，無法滿足80%的居民用電支出平穩。故在滿足生活用電成本得以彌補，工業用電成本減小的情況下，應更多地考慮民生，降低居民生活負擔。同時，對于低保人群等應實行提供免費電的政策，促進社會全面發展。

其二，在滿足用電基本需求的情況下，二、三檔電用戶盡量減少用電消費。這樣既可以降低生活成本，又可以減小環境壓力。以上海市為例，二、三檔電用戶用電支出增加的百分比隨其用電量的增加而上升，即邊際成本上升，故減少用電量成為居民的必然選擇。從環境角度來講，采用階梯電價可以提高居民的環保意識，利用經濟杠桿，采用環保型電氣設備，減少不必要的用電量，從而減少發電造成的污染，減小環境壓力。

其三，用電量按家庭常住人口分攤。避免因家庭人口較多或私房出租等造成的用戶電費負擔較大。合表用戶和一戶一表用戶受階梯電價的影響不同。農村及私房租房戶多為合表用戶，他們將因階梯電價支付更多成本，對已經較為貧困的他們造成更大的壓力。故應在實行階梯電價方案的同時，針對以上問題制定如按人均計算電費等的配套方案，從而降低低收入人群生活成本，促進社會的和諧發展。

————————

1.郭清、王小合、李曉惠等.2006.Lorenz曲線和Gini系數在社區衛生服務資源配置公平性評價中的應用[J].中國衛生經濟，25(1):50-53。

2.康璞、蔣翠俠.2009.貧困與收入分配不平等測度的參數與非參數方法[J].數量經濟技術經濟研，5:120-131。

3.劉樹杰、楊娟.2010.關于階梯電價的研究[J].價格理論與實踐，3：12-14。

4.劉宗謙、曹定愛.2004.收入分配不均等與Lorenz曲線"修補"[J].數量經濟技術經濟研究，21(8):46-54。

5.彭森.2012.把握形勢 抓住機遇 堅定不移地繼續深化改革開放[C].2012年全國經濟體制改革工作會議。

6.曾鳴、李娜、劉超.2011.基于效用函數的居民階梯電價方案的節電效果評估[J].華東電力，8。

7.朱柯丁、宋藝航、譚忠富等.2011.居民生活階梯電價設計優化模型[J].華東電力，6。