高空模擬試車臺擴壓器兩相流數值模擬①

崔立堃，江曉瑞，李 卓

(1.內蒙古工業大學 理學院，呼和浩特 010051;2.呼和浩特職業學院，呼和浩特 010051)

0 引言

高空模擬試車臺是能夠模擬發動機在空中飛行時的高度、速度等條件的地面試驗設備，基于常規真空設備在火箭發動機高空試車臺設計中的困難，國際上在20世紀50年代，即開展了采用超聲速引射器作為高空試車臺真空設備的實驗研究工作［1－2］，并取得了積極的成果。目前，二次喉道式擴壓器被動引射系統是國內測試發動機高空性能的主要手段，擴壓器是該系統中極其重要的部分，但擴壓器中存在著極其復雜的流場結構，這使得理論分析很難準確地評價擴壓器性能的好壞，通過大量吹風實驗來驗證擴壓器的性能，不僅耗費大量人力物力，而且實驗周期長。現代計算機技術和計算流體力學的迅速發展，使采用數值方法模擬求解超聲速擴壓器流場成為可能，通過數值計算驗證擴壓器的性能已被許多單位采用，并取得了一定的研究成果［3－6］，但針對固體火箭發動機具體燃燒產物對擴壓器流場結構及性能影響的研究卻幾乎沒有。

本文按照固體火箭發動機熱力學計算公式得到的燃燒產物主要成分，利用組元輸運模型和顆粒軌道模型，對被動式超聲速擴壓器內的兩相流動進行了數值模擬，并討論了Al2O3及粒徑大小對擴壓器內流場的影響，為擴壓器的設計研究提供參考。

1 物理模型

被動引射高模試車臺簡圖如圖1所示，該系統可模擬2 kPa左右的高空狀態。

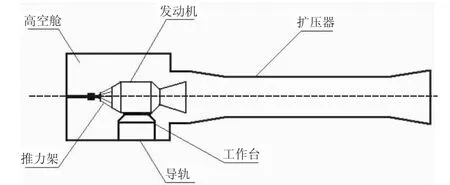
圖1 被動引射高模試車臺簡圖Fig.1 Schematic diagram of passive ejection altitude simulation facility

進行高模試車時，將發動機置于工作臺上，其前端通過推力架與承力墻連接。發動機點火前，用真空泵對高空艙預抽真空，將艙內壓強降至2 kPa。發動機點火后，隨燃燒室壓力增加，燃氣在噴管喉部迅速達到聲速，喉管內的激波向下游移動，直至移出噴管形成普朗特-邁耶爾膨脹流，此時引射系統進入最佳工作狀態。這種狀態下處于欠膨脹狀態的超音速燃氣流出噴管后迅速膨脹，壓強進一步降低，并與擴壓器壁面碰撞形成連續反射的激波。當燃氣流至二次喉道末端時，在環境反壓的作用下發生附面層分離，并形成激波串。在這個過程中，壓強逐漸升高、速度逐漸下降，最終以亞聲速進入擴壓器亞擴段，在亞擴段進一步減速增壓后排入大氣。這樣噴管出口處感受到的反壓非常低，從而模擬了一定高度的真空環境。同時，在整個過程中，燃氣會抽吸和夾帶高空艙內的空氣，使高空艙內也保持穩定的真空度。

2 數值計算模型

2.1 二維軸對稱控制方程

包含多種組分的二維軸對稱N-S方程以守恒形式［7］寫出如下:

其中

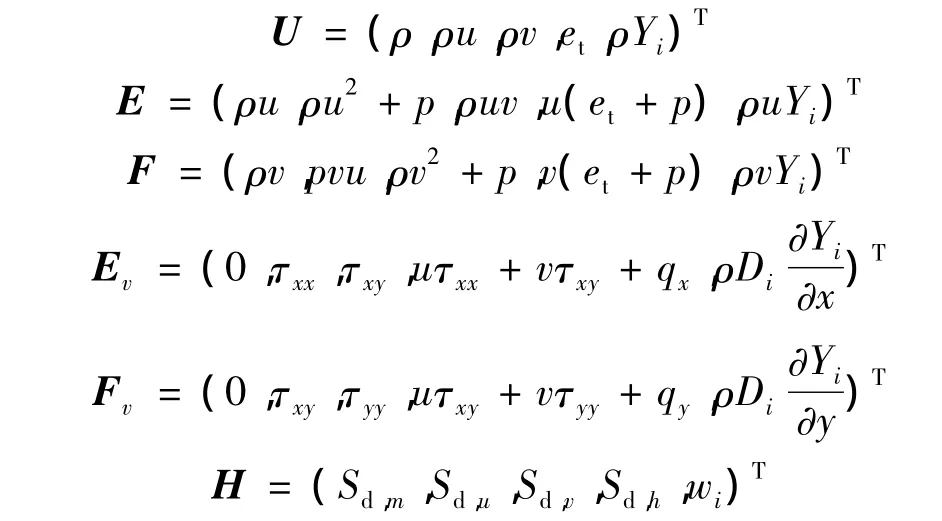
2.2 湍流模型

在動量方程中，涉及到湍流粘性系數μ1，它必須通過湍流模型求得，本文采用工程上廣泛使用的Spalart-Allmaras模型，該模型是一個相對簡單的模型，只求解一個有關渦粘性的輸運方程，計算量相對較小。此模型是專門用于涉及到束縛壁面流動的航空領域，對于受到反壓梯度作用的邊界層，能給出很好的模擬結果。湍流粘性系數μ1按下式計算:

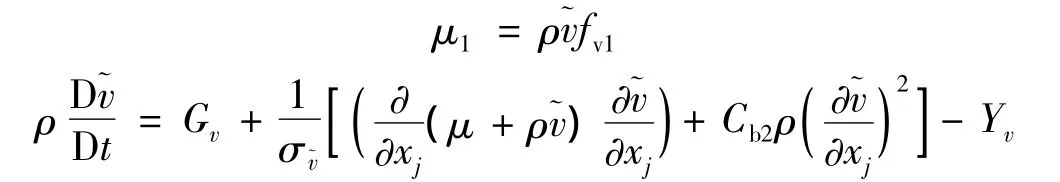
式中各系數的具體含義及表達式見文獻［8－9］。

2.3 離散相顆粒軌道模型

(1)流動絕能、無粘、不計重力作用，氣相是完全氣體。

(2)粒子為尺寸均一的球體，內部溫度均勻，忽略粒子所占的容積，認為粒子是離散相的，即粒子間互相沒有作用。

(3)僅考慮粒子與氣體間的阻力和傳熱作用，粒子對氣體壓力沒有貢獻，在流動中不膨脹做功，粒子不起化學反應。

顆粒相的基本方程［10－11］如下:

(1)顆粒的運動方程:

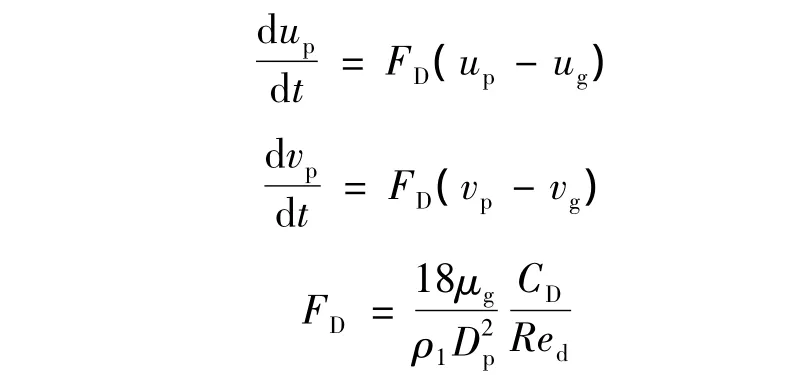
(2)顆粒的軌道方程:

(3)顆粒的加熱方程:

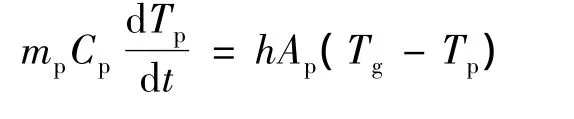
2.4 計算模型及參數

2.4.1 計算區域

計算區域見圖2，包括發動機噴管、擴壓器及部分外場。計算域的幾何和流場結構是軸對稱的。

圖2 計算域Fig.2 Computation domain

模擬介質為某推進劑燃燒產物的成分，推進劑按鋁18.2%、高氯酸銨67.2%、丁羥11%、葵二酸二辛酯3.1%、甲苯二異氰酸酯0.5%配比，噴管擴張比54.6，燃燒組分的計算采用布林克萊法，詳細的計算公式和方法及程序參見文獻［12］。

表1列出了計算得到的主要組分及其摩爾數。

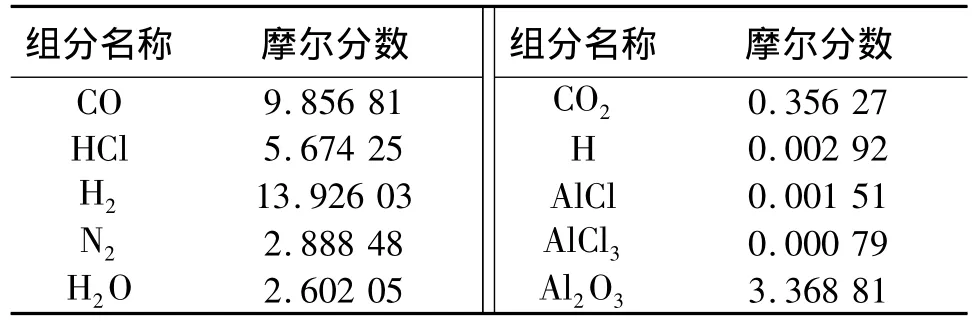
表1 燃氣中各組分含量Table 1 Content of each component in fuel

計算中，取占比重較大的前7種組分和最后1種組分。其中，前7 種物質 CO、HCl、H2、N2、H2O、CO2、H是氣態產物。最后1種組分Al2O3是凝相顆粒，由于相互間的破碎、聚合、碰撞等作用，粒徑會產生變化而非均一分布，不同的發動機在不同工況下燃氣中的粒子粒徑分布也會有所不同［13－14］。本文選取粒徑為5～100 μm間呈標準正態分布的 Al2O3顆粒，研究了Al2O3顆粒在擴壓器中的運動軌跡及其對流場的影響，并針對粒徑為 10、30、50、80 μm 4 種情況，研究了不同粒徑顆粒在擴壓器中的運動軌跡及其對流場的影響。整個過程采用凍結流進行計算。

2.4.2 邊界條件

選取某型號發動機的噴管及其高模試車時所用的擴壓器，對其幾何形狀進行適當的簡化，并添加部分外流場。其結構如圖2所示。計算中，燃氣入口為壓力入口，總壓4.5 MPa，總溫3 394 K;高空艙壓力入口為2 kPa。粒子由噴管入口進入，速度為100 m/s，溫度3 394 K，質量流量3 kg/s。

3 結果分析

3.1 Al2O3粒子對擴壓器流場的影響

圖3～圖5給出了不含粒子和含有粒子時的擴壓器馬赫數、溫度和壓強分布圖。其中，圖5中只給出了1 000～202 650 Pa間的壓強分布。

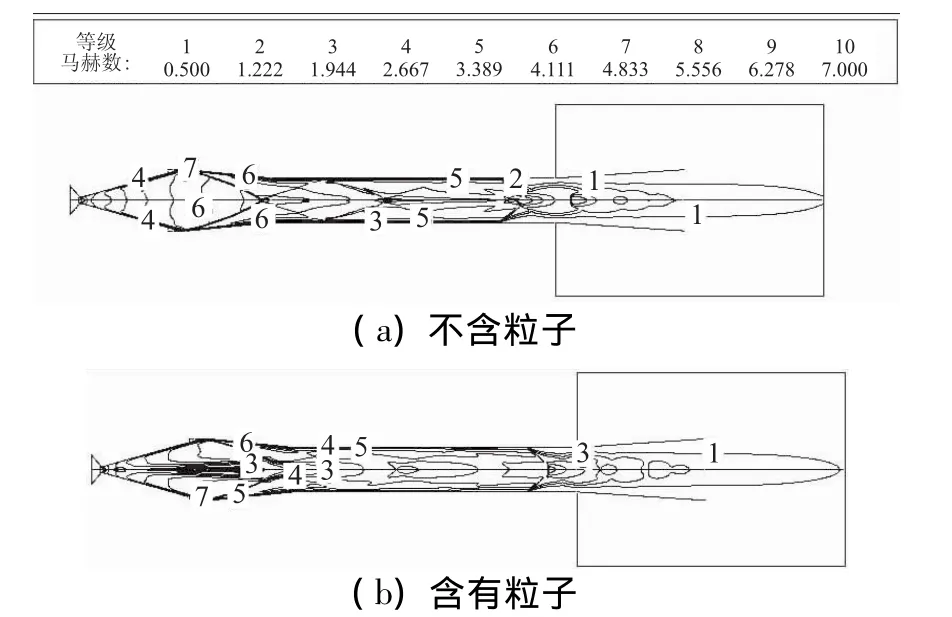
圖3 擴壓器馬赫數分布圖Fig.3 Mach number distribution in diffuser

圖4 擴壓器溫度分布圖Fig.4 Temperature distribution in diffuser

圖5 擴壓器壓強分布圖Fig.5 Pressure distribution in diffuser

在不考慮粒子的情況下，燃氣在擴壓器收縮段中形成斜激波，在軸線上相交之后形成反射激波，并打到擴壓器直管段壁面上，經壁面反射會再次形成斜激波，并交于軸線。在直管段末端產生壁面分離，形成一串復雜的激波串。

考慮粒子的影響時，粒子自噴管流出后在氣體作用下加速，并逐漸擴散，但粒徑較大的顆粒由于隨流性能較差主要集中在軸線附近，而粒徑較小的顆粒則逐漸彌漫至整個流場。粒子的存在會使流場的速度變得較緩慢。結合圖3～圖5可看出，在噴管軸線附近，由于聚集了較多的大粒徑粒子，其速度較無粒子時明顯為慢，溫度略高，在斜激波第一次相交的位置粒子與激波相互作用產生1個低速高溫的區域，進入二次喉道后，斜激波反射并再次相交，在相交處附近，粒子與激波再次碰撞，并形成低速高溫區，但由于此時粒子的分布已較均勻，且激波強度較小，該區域的速度變化量較小，至二次喉道的末端通過一串復雜的激波串后，速度降至Ma≤1，在擴張段再次減速增壓后排入大氣。

由圖5可看出流場中壓強的分布情況，在整個過程中，壓強隨激波的演變呈振蕩式上升，考慮粒子與不考慮粒子時基本一致。在激波交匯的區域附近，由于速度、溫度的變化，考慮粒子時壓強分布也會與不考慮粒子時有一定差別，特別在二次喉道的末端和擴張段中，形成了比不考慮粒子時更長的復雜激波串，激波串后壓強逐漸升至環境壓強。

圖6和圖7分別給出了不含粒子和含粒子2種情況下壓強和馬赫數沿擴壓器軸線的分布變化情況，其分布趨勢與文獻［5］一致。

圖6 擴壓器軸線上2種情況下馬赫數分布Fig.6 Mach number distribution on central axis of the diffuser in two situations

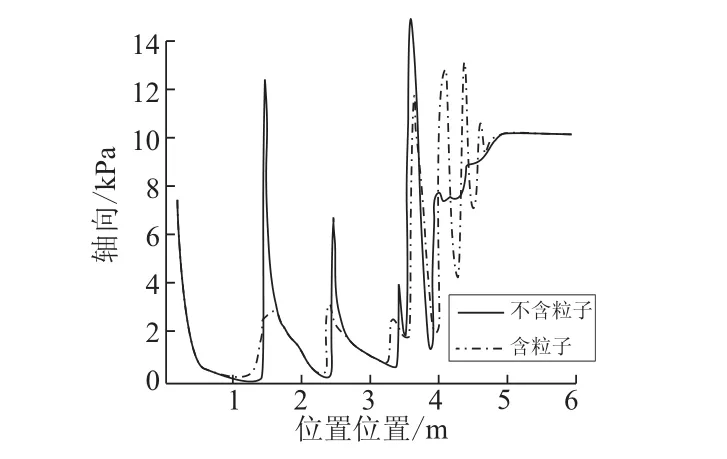
圖7 擴壓器軸線上2種情況下壓強分布Fig.7 Pressure distribution on central axis of the diffuser in two situations

從圖6和圖7可看出，2種情況下壓強均呈波動式上升，馬赫數均呈波動式下降。在不考慮粒子時，壓強的波動幅度比考慮粒子時更大，在二次喉道末端和擴張段，由于激波串較短波動次數較少，最后在出口處都升至環境壓強。由圖7可看出，不考慮粒子時，斜激波第一次交匯處形成了較大的馬赫數，而考慮粒子時，由于粒子的作用，使得軸線附近的速度低于周圍區域，且交匯處形成了低速區，故此處的馬赫數兩種情況下有較大區別。在二次喉道末端和擴張段不考慮粒子時，激波串較短波動次數也較少;考慮粒子時，波動次數較多，最終都以低于一個馬赫數的速度排入大氣。

3.2 Al2O3粒子粒徑大小對擴壓器流場的影響

圖8～圖11分別為不同粒徑時粒子軌跡、馬赫數、溫度和壓強的分布圖(圖下所注為粒徑)。

圖8 擴壓器粒子軌跡分布圖Fig.8 Particle vector distribution in diffuser

圖9 擴壓器馬赫數分布圖Fig.9 Mach number distribution in diffuser

圖10 擴壓器溫度分布圖Fig.10 Temperature distribution in diffuser

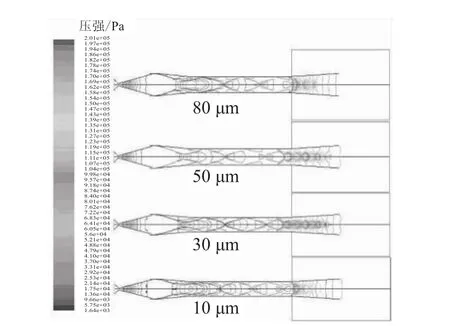
圖11 擴壓器壓強分布圖Fig.11 Pressure distribution in diffuser

由圖中可看出，不同粒徑下流場的基本流動規律:

(1)不同粒徑下流場分布存在諸多共同點:燃氣在擴壓器收縮段中形成斜激波，在軸線上相交之后形成反射激波，并打到擴壓器直管段壁面上。經壁面反射會再次形成斜激波并交于軸線。在直管段末端產生壁面分離，形成一串復雜的激波串。在整個過程中，馬赫數隨激波的演變呈振蕩式下降，并在直管段末端降至Ma=1之下。壓強則隨激波的演變而逐漸升高，并在擴張段逐漸升至環境壓強。

(2)粒徑不同時，粒子在流場中的分布存在較大不同。粒徑越小，其隨流性越好，易擴散，在流場中分布較廣;粒徑越大，其隨流性越差，不易于擴散，粒子分布更集中于軸線附近。由圖8可看出，粒徑為10 μm時，粒子通過噴管喉部后開始擴散，到噴管出口處時，已分布于出口橫截面的大部分區域，至擴壓器收縮段中后部時，已擴散至整個橫截面上，對擴壓器壁面造成沖刷。隨著粒徑的增加，粒子的擴散速度明顯變慢，粒子與擴壓器壁面接觸的位置隨著粒徑的增大向后移動。當粒徑為80 μm時，粒子在二次喉道的中后部，才擴散至整個擴壓器的橫截面上。

(3)粒子在流場中分布情況的不同，使得流場結構產生明顯變化。由于粒子的運動速度較慢，且會對周圍的氣體流動產生阻礙，所以粒子密集的區域流場流速較慢。由圖9可看出，噴管中軸線附近的流速明顯低于周邊區域。由于粒徑越大粒子分布越集中，所以粒徑越大時，噴管中低速區就越小，低速區的速度也越低。進入擴壓器后，速度場的分布也受到影響而產生差別。另一方面，粒子對溫度場也產生較大影響，粒子集中的區域溫度較高。

(4)不同粒徑時，都會在二次喉道末端出現壁面分離，并產生復雜的激波串，通過激波串后，降至亞聲速。但不同粒徑下，產生分離的位置和激波串的機構有較大差別。由圖11可看出，當粒徑為30 μm時，壁面分離出現的最早，激波串的長度最大。

表2給出了4種情況下擴壓器壁面上的最高溫度和平均溫度。

表2 不同粒徑時擴壓器壁面最高溫度和平均溫度Table 2 The highest temperature and average temperature on the wall of diffuser with different particle sizes

由表2可看出，4種情況下壁面的最高溫度差別不大，都在3 200 K左右。平均溫度差別較大，且粒徑越小，平均溫度越高。這可能是由于粒徑小時，粒子擴散快，較早的與擴壓器壁面接觸，對擴壓器壁面沖刷和在壁面上的沉積較嚴重，將更多的熱量帶至壁面上，這樣高的溫度對擴壓器的散熱提出了很高要求。因此，在設計擴壓器時，必須充分考慮其散熱問題。

4 結論

(1)在引射器中存在著非常復雜的超聲速流場，形成了有一定長度的激波串，氣流通過激波減速增壓。因此，為了達到最大的壓力恢復，應保證擴壓器有一定的長徑比。

(2)不同粒徑的粒子在流場中的擴散速度不同，對擴壓器壁面的沖刷位置不同。當粒徑為10 μm時，粒子在擴壓器收縮段中后部，就已擴散至整個橫截面上，并對之后的擴壓器壁面造成沖刷。當粒徑為80 μm時，粒子在二次喉道的中后部，才擴散至整個擴壓器的橫截面上，并形成沖刷。

(3)不同大小的粒子對擴壓器壁面的沖刷和沉積程度不同，帶至擴壓器表面的熱量不同，使得擴壓器表面的平均溫度有較大差別。但壁面的最高溫度與粒徑大小關系不太密切，基本在3 200 K左右。

［1］Bauer R C，German R.The effect of second throat geometry on the performance of ejectors without induced flow［R］.AEDC-TN-61-133.

［2］Jones W L，Frice H G and Lorenzo C F.Experimental study of zero-flow ejectors using gasous nitrogen［R］.NASA TN D-203.

［3］丁學進，王志浩，劉曉麗.高空模擬試車臺擴壓器數值分析［J］.重慶科技學院學報(自然科學版)，2008，10(1):61-63.

［4］張志峰，劉洋，蔡體敏.隨機顆粒軌道模型在長尾噴管發動機中的應用［J］.固體火箭技術，2007，30(5):376-380.

［5］徐萬武，譚建國，王振國.高空模擬試車臺超聲速引射器數值研究［J］.固體火箭技術，2003，26(2):71-74.

［6］朱子勇，李培昌，瞿騫.某型號火箭發動機高空模擬試驗中擴壓器的數值計算與試驗比較［J］.航天器環境工程，2010，27(2):231-237.

［7］武曉松，陳軍，等.固體火箭發動機工作過程數值仿真［M］.北京:高等教育出版社，2006.

［8］Spalart R，Allmaras S.A one-equation turbulence model for aerodynamic flows［R］.AIAA 92-0439.

［9］周猛.超聲速高聲速流場理論研究［D］.國防科技大學，2001.

［10］周力行.湍流兩相流動與燃燒的數值模擬［M］.北京:清華大學出版社，1991.

［11］趙云華，何玉榮，等.煤粉顆粒群著火和燃燒過程的數值模擬［J］.燃燒科學與技術，2007，13(2):107-112.

［12］QJ 1393A—2004.固體火箭發動機熱力學計算方法和計算程序［S］.中華人民共和國航天行業標準，2004.

［13］張明信，王國志，魏建維，等.固體推進劑燃燒中凝相粒子的激光全息測試［J］.固體火箭技術，2000，23(1):70-73.

［14］李越森，葉定友.高過載下固體發動機內Al2O3粒子運動狀況的數值模擬［J］.固體火箭技術，2008，31(1):24-27.