基于排序值差異與被引次數的論文分區研究

●郭 強，趙 瑾

(1．鄭州大學 信息管理系，鄭州 450001；2．中國人民解放軍陸軍軍官學院 軍事運籌教研室，合肥230031)

論文的被引次數與論文的學術影響力之間所具有的相關性使得論文的被引次數能夠作為對論文影響力進行反映的基本指標，同時數字與網絡環境的發展也使得論文被引次數的獲取具有便捷性，所以被引次數及其相關復合指標也滿足指標具有可測性的要求，需要指出在利用被引次數對論文的影響力進行描述時有時會需要對被引次數的取值大小進行較為明確的劃分，例如，與期刊類似，需要對關于某主題的論文進行大致的分類，由此來得到關于該主題的代表性論文，在對論文進行分區的過程中，如果論文關于被引次數具有負指數分布的特征并近似滿足布拉德福分布的要求，那么可以嘗試對論文進行傳統的布拉德福分區。但是對于所選取的關于某主題的論文而言，如果較多的論文均具有相對較小的被引次數，那么在末尾分區中可能會包含明顯偏多的論文，從而體現為在末尾或靠后分區處會具有偏高的論文數相繼比，這種情況會在一定程度上影響對論文進行布拉德福分區的合理性。如果將末尾分區處偏高的相繼比視為特異值，那么在保證分區合理性的同時也會影響到末尾分區中論文的劃分。是否能夠直接對論文被引次數的取值大小進行大致的判定，并由此來對論文直接進行分區，從而避免在論文分區中出現的格魯斯下垂。由此，本文希望能夠對被引次數的取值進行劃分，并在此基礎上根據論文被引次數的實際取值來嘗試對論文進行分區。

1 布拉德福分區

從直觀上，關于某主題的論文會具有負指數分布的特征，例如相對較多的論文有著相對較低的被引次數，同時相對較少的論文的被引次數會相對較高。假設圖書情報類論文的最大引文年限為3年，那么選取2004年6月以及在2005年6月出版的圖書情報類期刊論文作為考察對象，數據的統計時間選取為2011年10月。這樣選取的原因是由于論文的最大引文年限為3年，按照所選取的統計時間論文的考察時長會超過5年，從直觀上在最大引文年限之后論文的受利用程度會隨時間呈現下降的趨勢，不嚴格地在該時段內的被引次數能夠對論文受利用情況的主要部分進行近似的反映，或者說，在該時段內的被引次數足夠大，從而能夠對論文的被引次數進行近似的表示。另外，在網絡環境下，論文入庫時間的差異會影響論文被引次數之間的可比性。如果能夠認為這里的考察時長為足夠長，從而對具有不同入庫時間的論文的被引用情況均能夠進行大致的體現，那么在這里沒有將入庫時間的差異所帶來的影響考慮在內。本文選取CNKI的鏡像站版作為數據來源，對于所選取的論文樣本以及考察時長，每篇論文均有在時段內的被引次數并將其近似為論文的總的被引次數，將論文按照該被引次數降序排列，得到論文的累積量與被引次數的累積量之間的關系，如圖1所示。

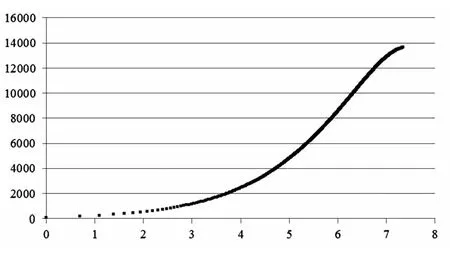
圖1 論文的累積量與被引次數累積量之間的關系

在圖1中，橫軸為論文累積量的對數，縱軸為累積被引次數。如果取分區數為3，那么此時核心區的論文數能夠近似為136，并且各個分區中的累積被引次數的平均值為4551，標準差僅為12。此時，各分區中論文數的相繼比的平均值為2.891，并且標準差為0.771。如果取分區數為5，那么能夠看到在末尾分區處相對偏高的相繼比。此時，各個分區中的論文數的相繼比分別為1.859、1.571、1.631以及2.872，其平均值為1.983，并且標準差能夠達到0.605。同時，除了分區描述之外，在圖1中也能夠看到在被引次數偏低處的格魯斯下垂的出現。另外，被引次數的累積量與論文累積量之間的關系能夠與布魯克斯公式相吻合，例如取分區數為3時，所得到的分段擬合方程為m=116.46n0.755以及m=4042.7Ln n-15563，并且核心區與非核心區的判定系數分別為0.998以及0.994，其中m為累積被引次數，n為相應的論文累積量。所以對于被引次數在論文中的分布而言，從直觀上會有相對較多的論文具有相對較低的被引次數，同時如果能夠近似地認為這里的分布性質具有一定的布拉德福分布特征并由此來對論文進行分區時，那么當選取分區數為3時，各分區的論文累積數分別為136、319以及1096。

2 被引次數分區

對于所選取的論文樣本，每篇論文均有與其對應的被引次數以及施引期刊的影響因子之和，其中當施引期刊相同時對其影響因子進行累計求和。

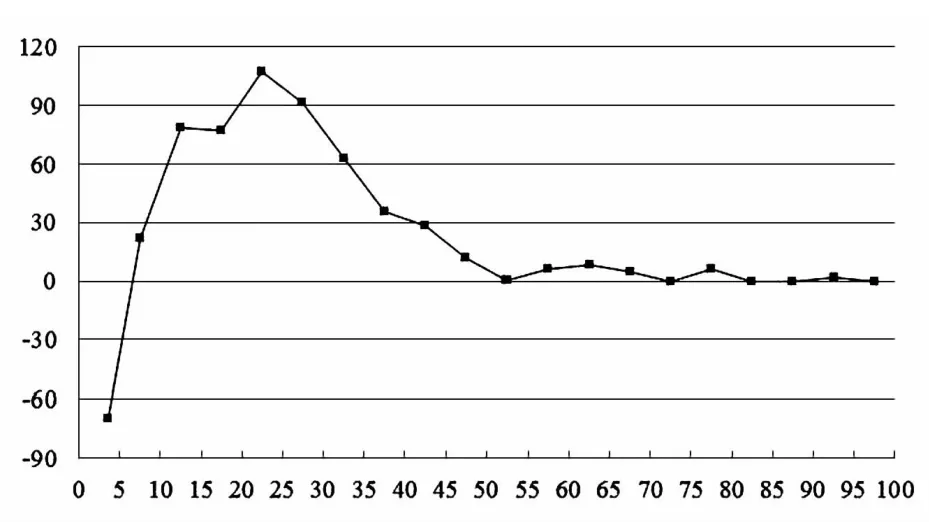
圖2 按照影響因子之和與被引次數的排序值差值與論文被引次數的關系

在圖2中，橫軸為論文的被引次數，將論文按照影響因子之和以及被引次數分別進行降序排列，得到論文在這兩個序列中的排序值。圖2中各點的縱坐標分別為所在被引次數范圍內的論文排序值差值的平均值。對于這里的被引次數的劃分間隔，當被引次數小于5時會出現差值為負的情形；當被引次數大于50時，在兩個序列中論文的排序情況沒有發生顯著的變化。而在被引次數的其余范圍內，與按照被引次數進行降序排列相比，論文按照影響因子之和進行排序所得到的排序值會相對較高。

一種可能的原因是由于在被引次數相對較高的區域，對于具有偏高被引次數的論文而言，其施引期刊的影響力在總體上也往往會相對較高。同時，當論文的被引次數相對較高以至于達到一定程度時，對于該區域的每篇論文而言，其施引期刊的影響因子的取值范圍以及數值分布情況在總體上也會具有相對較小的差異。由此能夠近似地認為，在該區域中論文的被引次數與論文施引期刊的影響因子之和會具有相同的降低速度，例如論文的被引次數由50降低至25時，施引期刊的影響因子的大小范圍與總體分布特征近似相同，這意味著僅是影響因子的分布密度或者是施引期刊的數量會有差異。而當論文的被引次數足夠高時，例如對于被引次數分別為50與25的兩篇論文，前者的施引期刊的影響因子之和能夠近似等于后者的影響因子之和的兩倍。同時，對于被引次數的任意降低比例，類似地由于不同論文的施引期刊的影響因子具有相似的取值范圍以及分布性質，所以在影響因子的任一分布區域施引期刊的分布密度均具有相同的降低比例。另外，由于論文的總被引次數等于各區域的被引次數之和，所以該降低比例與上述被引次數的降低比例相同，并且當區域分割得足夠細時，在各區域中的影響因子能夠被認為近似相等。這樣，在各區域中的施引期刊影響因子之和僅由相應區域中的施引期刊的數量來確定，從而在各區域中的影響因子之和也具有相同的降低比例。將各區域中的影響因子之和進行累計后能夠得到論文的影響因子之和同樣具有相同的降低比例，由此可以認為，在被引次數相對較高的區域，論文的被引次數與論文的影響因子之和具有相同的降低速度。分別按照被引次數與影響因子之和進行降序排列，發現所得到的兩個序列中這兩篇文章與其他論文的相對位置不會發生改變，同時論文在排序上的這種對應關系也意味著在所得到的兩個序列中，在被引次數相對較高的范圍內以及在對應的影響因子之和相對較高的范圍內會具有相似的論文分布，只是論文的被引次數與論文的影響因子之和的實際取值范圍會存在差異。對于被引次數相對較高的論文而言，在分別按照被引次數以及按照影響因子之和進行排序的序列中的論文排名也不會發生變化，并且在所得到的兩個序列中任意的被引次數處與降低相應比例的影響因子之和處的論文是相同的。需要指出的是，這些考慮均建立在一定的假設基礎上，也就是被引次數相對較高的論文其施引期刊的影響因子之和也會相對較高，同時被引次數相對居中的論文的影響因子之和也會較為居中，對于被引次數偏低的論文也有類似的情形。或者是將論文分別按照被引次數以及施引期刊的影響因子之和進行降序排列，并且只針對這三個部分進行粗略的分區，那么由這兩個序列所得到的對應分區會包含同樣的論文，這樣當考察論文在分別按照被引次數與影響因子之和進行排序時的排名變化時只需要考慮該論文在所屬分區內的排序變化情況。另外，在被引次數相對居中的區域，隨著論文被引次數的降低，論文的施引期刊在影響力上也會有所下降或是會有所差異，所以在這里假設在該區域中對于被引次數相對較高的論文而言其施引期刊的影響因子會具有較大的變化范圍，同時與被引次數相對較低的論文相比，前者的變化范圍的最大值會相對較高，而兩者變化范圍的最小值會近似相等。仍然假設不同論文的施引期刊的影響因子在其變化范圍內具有相同的分布特征，由此能夠得到影響因子之和的降低比例會高于論文被引次數的降低比例，例如對施引期刊影響因子的變化范圍進行等分，并且使得不同論文的分區數量相同，那么對于被引次數不同的任意兩篇論文而言，所得的分區長度之間的比例關系等于施引期刊影響因子的取值范圍之間的比例關系。對應于這兩篇文章的被引次數的降低比例，由于影響因子的分布狀況沒有發生變化，所以將影響因子的分布范圍進行等分時，各區間施引期刊的數量的相互之間的比例關系不會發生改變，各區間中的施引期刊的數量均會同比例降低，并且該比例等于上述論文被引次數的降低比例。進一步地，當分割得足夠細時，各個分區中的影響因子能夠被認為近似相等，那么施引期刊的影響因子之和近似等于各分區的施引期刊的數量與所屬分區的影響因子的乘積的累計和，因為各個分區的施引期刊的數量均與被引次數的降低比例相同，同時與被引次數相對較高的論文的對應分區相比，被引次數較低的論文在各個分區的施引期刊的影響因子會相對較小。其原因是，由于影響因子變化范圍的最小值會接近于零，如果能夠假設影響因子變化范圍的最小值為零，那么被引次數較低的論文在對應分點處的影響因子均會降低相同的比例，并且該比例與上述影響因子取值范圍之間的比例關系相同，即使這種變化范圍的最小值不為零并且假設為α，那么兩篇論文在對應分點處的影響因子的比值會隨著分點的不同而發生改變，并且該比值能夠等于(α+χα’i)/(α+α’i)，其中χ為與這兩篇論文對應的影響因子取值范圍的比例關系并且取χ大于1，α’為與被引次數較低的論文相對應的取值范圍與總的分區數量的比值，i為按分點處的影響因子對分點進行升序排列后的分點序號。由于χ大于1，所以被引次數較高的論文的各個分點處的施引期刊影響因子均大于被引次數較低的論文在相應分點處的影響因子，這樣影響因子之和的降低比例就會高于論文的被引次數的降低比例，例如當論文的被引次數由18降低至9時，在該區域中對于具有不同被引次數的論文而言，論文的施引期刊的影響力也會有差異。在假設施引期刊的影響因子具有相同的分布特征的基礎上，對兩篇論文的影響因子的分布范圍分別進行等分后，對于被引次數較低的論文，其各分區的施引期刊的數量均會比被引次數較高的論文在對應分區的施引期刊數量降低50%，從而保證不同論文的影響因子的分布特征不會發生變化。同樣，當對分布范圍分割的足夠細時，論文施引期刊的影響因子之和近似等于各分區的影響因子與各個分區的施引期刊的數量的乘積的累計和，在各個分區中施引期刊數量的降低比例與論文被引次數的降低比例相同也為50%。同時，對于被引次數為18的論文，其施引期刊的影響因子具有相對較大的取值范圍，在假設這種變化范圍具有相近的最小值的基礎上，被引次數為9的論文在各分區的對應分點處的影響因子會相對較小，所以后者具有的施引期刊影響因子之和的降低比例會高于論文被引次數的降低比例。進一步地，如果施引期刊的影響因子之和與論文的被引次數相比具有更高的降低比例，那么在按照被引次數以及影響因子之和分別進行降序排序的論文序列中，能夠分別得到被引次數的累計百分比與論文數量的累計百分比之間的關系以及影響因子之和的累計百分比與論文數量的累計百分比之間的關系。在圖3中能夠看到這兩種關系之間的一致性。這說明，被引次數與影響因子之和在兩個論文序列中分布的相似關系，僅是被引次數與影響因子之和的實際取值范圍會存在差異，而在這兩個論文序列中任意的被引次數處與降低相應比例的影響因子之和處的論文可以是不相同的。這樣對于被引次數相對居中的任意的論文而言，由于其施引期刊影響因子之和的降低比例會相對較高，所以與按照被引次數進行降序排列相比，這篇論文在按照影響因子之和進行排序的序列中的論文排序值也會有所提升。在圖3中，橫軸為論文的累計百分比，縱軸分別為影響因子之和以及被引次數的累計百分比，并且對應于不同的論文的累積百分比，影響因子之和的累計百分比均高于被引次數的累計百分比，其中累計百分比差值的最大值為5.251%，所以在這里假設上述兩種關系之間具有近似的一致性。

圖3 影響因子之和與被引次數的累積量與論文累積量之間的關系

在被引次數相對較低的區域，能夠得到影響因子之和的降低比例會低于論文被引次數的降低比例，例如當論文的被引次數由2降低至1時，論文的被引質量往往不會降低50%的比例，這兩篇論文通常會具有程度相當的被引質量。由于施引期刊的影響因子之和能夠將論文被引情況中施引期刊的數量與質量均納入在內，所以如果能夠將論文的施引期刊的影響因子之和對應于論文的被引質量，那么施引期刊的影響因子之和的也不會降低50%的比例，從而低于論文被引次數的降低比例。進一步地，由于在按照被引次數以及影響因子之和進行降序排列的論文序列中，被引次數以及影響因子之和隨論文累積量的變化具有其一致性，也意味著被引次數與影響因子之和在論文序列中分布的相似性，所以當論文的被引次數的降低比例相對較高時，與按照被引次數進行排序相比，論文在按照影響因子之和進行降序排列的序列中會具有相對較小的排序值。

這樣，在被引次數相對較低的區域，論文在按照被引次數以及按照影響因子之和分別進行排序后所得到的排序值會有差異，且后者的排序值小于前者的排序值。同時，在被引次數相對居中的區域，論文在按照被引次數降序排列的序列中的排序值會相對較低，或者說，當被引次數較為居中時，后者的排序值會大于前者的排序值。另外，在被引次數相對較高的區域，按照被引次數以及按照影響因子之和分別進行降序排列時所得的論文排序值不會發生顯著的改變。所以當論文的被引次數發生變化時，論文在分別按照不同的指標進行排序時的排名情況也會發生變化，由此是否能夠考慮將論文在兩個序列中的排名變化情況來作為對論文被引次數實際取值的反映。

另外，也可以將論文按照其被引次數進行降序排列，其中具有相同被引次數的論文的相互之間的排序是任意的，由此能夠得到所有論文的被引次數序列，同時每篇論文均有施引期刊的影響因子之和與其對應，所以也能夠得到相應的影響因子之和序列，在被引次數序列中對任意的被引次數用其后繼的被引次數與該被引次數相除來得到被引次數的相繼比序列，同理，能夠得到影響因子之和的相繼比序列。在圖4中，橫軸為相繼比的序號，由于論文是按照被引次數降序排列，所以相繼比序號的增加能夠與論文被引次數的減少相對應，縱軸為被引次數以及影響因子之和的相繼比。需要指出的是，圖4只是對相繼比變化趨勢的近似反映，并且只考慮了被引次數不為零的論文且論文數為1551，在被引次數相對較低的區域影響因子之和的相繼比位于被引次數相繼比的上方，能夠近似地反映在該區域中論文的影響因子之和的降低速度會低于其被引次數的降低速度。當按照影響因子之和進行降序排列時，論文的排序值會有所下降，在被引次數相對居中的區域，影響因子之和的相繼比位于被引次數相繼比的下方，從而意味著影響因子之和的降低速度會高于被引次數的減低速度，在一定程度上反映了當按照論文的影響因子之和進行排序時，與按照被引次數降序排列相比，論文的排序值會有所上升，同時在被引次數相對較高的區域，或者更為確切地是對應于兩條曲線接近重合的區域，影響因子之和與被引次數具有相近的降低速度。在分別按照被引次數以及影響因子之和進行排列的序列中，論文會具有相近的排序值，與圖2中排序值沒有發生明顯變化的區域相對應，這兩條曲線接近重合的區域為被引次數在50以上的區域，對應的相繼比序號為14。需要指出，這種考慮是建立在按照被引次數以及影響因子之和分別進行降序排列時論文具有相似或一致分布的基礎上。另外兩條曲線的起始縱坐標均近似地取為1的原因是所在區域的被引次數與影響因子之和均會相對較高，所以對被引次數降序排列后后繼被引次數的相對變化比例會相對較小，盡管此時的影響因子之和并沒有降序排列，但是該區域中相對較高的影響因子之和也同樣會帶來后繼影響因子之和的相對較小的變化比例。其次，兩條曲線的另一個交點的橫坐標或者是相繼比的序號取為893，是對應于圖2中的排序值的差值由正變為負時所對應的被引次數得到的。

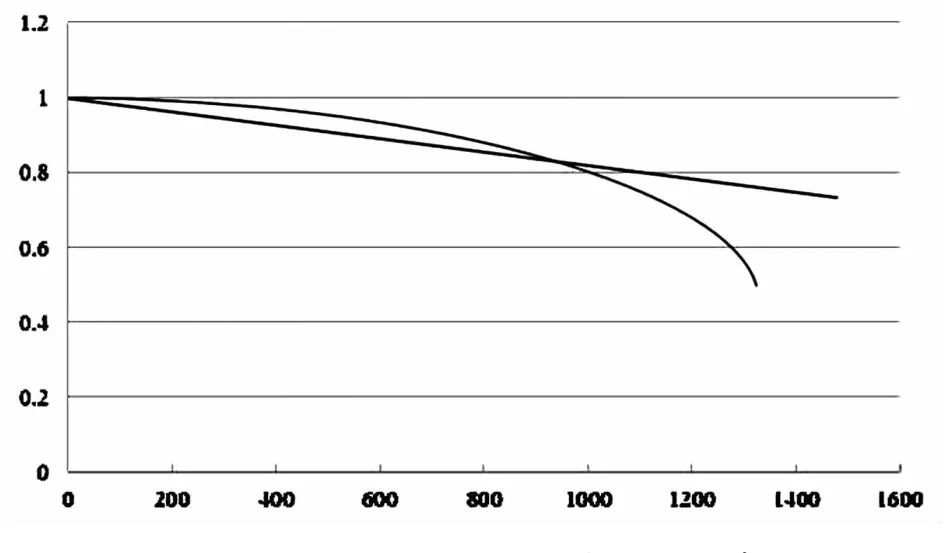
圖4 影響因子之和與被引次數的相繼比與被引次數之間的關系

如果能夠認為論文排序的變化情況與論文的被引次數相關聯，能否利用這種變化情況來對被引次數的取值進行反映，由此來對被引次數以及相應的論文進行分區。按照圖2中排序值差值的變化情況，將被引次數以及論文進行分區為被引次數大于50，被引次數小于5，以及被引次數在5與50之間的區域，同時各分區的論文數分別為14,659，以及878篇，需要指出這里的分區是較為近似的，需要進一步調整，例如減小圖2中的被引次數的劃分間隔。

3 結束語

論文的被引次數與論文學術影響力之間的普遍相關性是被引次數成為基本指標的一種原因，這也是使得被引次數與論文排序變化情況之間具有關聯性的基礎。類似地，當被引次數發生變化時，論文按照不同的影響力描述體系來得到的影響力分值的排名情況也會發生改變，并且所得論文排序值的差值隨著被引次數也會具有相近的取值變化情況，例如當被引次數小于10時考慮施引期刊的差異與考慮被引次數絕對量的論文影響力的排序值的差值會小于零；當被引次數大于70時，論文按照這兩種論文影響力的排序情況不會發生顯著的變化。如果論文的被引次數位于10與70之間的區域，那么排序值的差值會大于零，其中的論文影響力分值是由文獻[1]中的指標體系并考慮論文的下載情況來得到，所以能否利用這種被引次數與排名變化情況的關聯性來對被引次數的大小進行側面地反映，對被引次數進行劃分以及對論文按照其被引次數來進行分區。另外，被引次數能夠作為對論文影響力的表征，并且論文的排序情況也會隨著論文的被引次數發生變化，那么論文排序情況的變化是否也能夠成為對論文影響力的側面反映。[1]金晶,等.不同學科領域自然科學論文學術影響力評價與比較的可行性研究[J].科技管理研究,2010,(14)：279－284.