直擴/跳頻測控信號捕獲算法研究*

王金寶，楊文革，章蘭英

(1.裝備指揮技術學院，北京 101416;2.酒泉衛星發射中心，甘肅酒泉 732750)

0 引言

隨著空天電磁環境的日趨復雜，航天測控系統作為一種保障空間航天器正常運轉的系統，其對電磁對抗性的要求也日趨提高。現行統一載波測控系統抗干擾性能較差［1］;而統一擴頻測控隨著盲檢測與盲估計技術的發展，其抗干擾性能遭受到嚴峻挑戰。直擴/跳頻混合擴頻體制綜合了直擴和跳頻的優點，是國內外公認的最富有生命力的抗干擾體制，將這一體制引入到測控系統中，將能有效提高測控系統的電磁對抗能力。

直擴/跳頻(direct sequence spread spectrum/frequency hopping，DS/FH)混合擴頻系統在通信方面應用廣泛，美國的國防衛星通信系統(DSCS)、北約的衛星鏈路(NATO)［2］均采用了直擴/跳頻混合擴頻技術。但關于DS/FH擴頻信號用于航天測控的文獻少見論述。文獻［3］論證了DS/FH擴頻信號具有優良的測距和測速性能。文獻［4］提出了混合擴頻系統雙極同步技術，因跳頻與直擴的同步分開進行，降低了同步系統的抗干擾性能。文獻［5］提出一種利用導頻信道傳輸同步偽碼的方法，但其捕獲時間慢，不適合高動態環境。文獻［6］提出采用快速頻率識別，實現混合系統的快速同步方案，但只考慮了跳頻圖案和偽碼相位的二維同步。文獻［7］提出了DS/FH測控信號的同步方案，并研究了測控信號的捕獲性能。本文在文獻［7］的基礎上，針對混合測控信號特點，進一步優化了混合擴頻測控信號的捕獲方案，對捕獲方法進行了改進，其仿真結果表明了改進的有效性。

1 混合擴頻測控信號的捕獲方案

1.1 混合測控信號的不同之處

與一般混合擴頻通信系統相比，航天測控有一些自身的特點。一是信號動態范圍大，除同步軌道外，目標與測控站間的相對速度使得測控信號產生的多普勒頻率達百kHz量級;二是航天測控對目標有跟蹤的要求;三是接收信號信噪比很低。測控鏈路的傳輸距離很遠，鏈路損耗很大，即使是低軌道衛星其測控鏈路損耗也在190 dB以上［8］。由于這些特殊問題的存在，使得混擴測控信號的捕獲與一般的混合擴頻通信有所不同。由于大多普勒存在，使得對其信號的捕獲由一般意義上對跳頻圖案和偽碼相位的二維搜索轉為對跳頻圖案、偽碼相位和載波多普勒的三維搜索，并且在一個本地駐留時間內要完成對偽碼與載波的二維搜索;另外測控對于跟蹤的需求，也要求捕獲的結果盡可能準確，以利于跟蹤的快速建立與穩定。綜合考慮，本文采用快速掃描等待法實現跳頻圖案的捕獲;采用適用于低信噪、高動態環境下部分匹配濾波-快速傅里葉變換(partial matched filter-fast Fourier transform，PMF-FFT)的方法，實現直擴的二維快捕。同時對PMF進行凱澤加權，提高相關幅度;采用拋物線測頻法來減小多普勒的估計誤差，從而使捕獲結果更為精確。

1.2 捕獲方案

其捕獲過程如圖1所示。

圖1 直擴/跳頻混合擴頻測控信號捕獲方案Fig.1 Acquisition scheme of DS/FH signal for TT＆C

整個捕獲過程在處理器的控制下進行。開始時頻率合成器工作在快速掃描模式，它以H倍于發端的頻率跳變速率輸出本地參考頻率，當本地參考頻率為f'j，接收信號頻率為fj，即可經過混頻濾波A/D轉換得到數字中頻信號。數字中頻信號先與載波NCO(number controlled oscillator)相乘轉換為 I，Q兩路基頻信號，與本地載波相乘后的結果送入凱澤加窗PMF-FFT的直擴捕獲電路。送來的信號先與本地偽碼進行相乘，而后與凱澤窗進行加權，再經部分匹配濾波進行累加求和，最后經FFT進行變換輸出信號的幅度和多普勒頻率估算值。輸出的信號幅值與門限VT進行比較，如果在本地駐留時間T'h內相關檢測值均小于門限VT，則捕獲失敗轉入下一頻點繼續快速掃描;反之則轉入驗證階段。驗證階段與上述過程類似，只是當信號幅值通過門限VT時，拋物線測頻部分重新開始對FFT輸出的多普勒值進行估算并將估算結果送入處理器，處理器隨后對載波NCO進行修正，從而形成更為接近的零中頻信號，驗證成功則轉入跟蹤階段。圖中頻率合成器的等待搜索模式工作在跟蹤的初始階段。

PMF-FFT的偽碼捕獲方法雖能適應高動態、低信噪環境下的混擴的捕獲［9］，但PMF-FFT法同時也存在2個問題，下面將對這2個缺陷進行改進。

2 捕獲方法的改進

2.1 PMF-FFT基本原理

基于PMF-FFT的載波并行法就是在一個碼搜索單元內，同時搜索所有的頻率偏移量，將二維的搜索變為在碼搜索方向上一維的搜索［10］。如圖2所示，在此結構下，本地偽碼與輸入信號偽碼之間保持相對滑動，設PMF長度為 L，共有 N個，LN=M，M為偽碼周期長度。進入PMF的L個數據相關后進行累加，得到N個累加輸出值，這N個輸出值進行K(K≥N)點的FFT運算，對變換后的頻譜進行分析，得到多普勒頻率值，若其值超過所設定的門限，則此時對應的時域和頻域的值即為偽碼相位和多普勒頻率的估計值，從而完成載波和偽碼相位的二維并行捕獲。

設PMF參數設置與上面相同，碼元相位估計正確且不計初始相位，也不考慮數據的影響，相關器的2個輸入分別為本地偽碼r(n)、接收偽碼r(n)·exp(j2πfdnTs)，其中Ts為采樣間隔。第i個PMF的歸一化輸出為

對N個PMF的輸出作FFT變換，得到

圖2 基于PMF-FFT的載波并行捕獲原理框圖Fig.2 Parallel carrier acquisition theory figure based on PMF-FFT

基于PMF-FFT方法存在2個缺陷，一個是累加后的譜峰會出現“扇形衰減”，其原因是在頻域內K點FFT運算相當于K個并行的窄帶濾波器，相鄰2個窄帶濾波器因為主瓣的衰減從而導致扇形衰減的出現，這使得所搜索的信號幅值將會大大減小;另一個是進行頻率估計的時候存在“柵欄效應”，其原因是用FFT計算的頻譜，只限于基頻(1/MTs)的整數倍而不能將頻譜視為一連續函數而產生的。只有當頻偏fd為頻率分辨率(1/MTs)的整數倍時，其估計值才是準確的。這2個缺陷直接影響著捕獲難易和對多普勒的頻率估計的準確性，因此有必要加以改進。

2.2 對扇形衰減的改進

(1)改進原理

對扇形衰減的改進從對PMF的2種理解入手。一種是從相關累加的方面進行理解。參數設置與2.1相同，經相關后輸出結果為

x(n)=r(n)×r(n)exp(j2πfdnTs)=exp(j2πfdnTs)，則PMF的各部分匹配濾波器輸出結果為

對PMF還可以從信號處理方面進行理解。首先，相關后M點數據x(n)和長度為L點的矩形窗w(n)進行卷積，該過程完成對x(n)的低通濾波，卷積結果為

然后，以抽取率L(即每隔L-1個數據取一個)對r(m)進行抽取，對數據進行降速處理。抽取后信號為

比較式(2)和式(4)可知，M點數據x(n)與長度為L點的矩形窗w(n)先卷積再以抽取率L對其進行抽取得到的序列，與直接對M點數據x(n)的每L點求和得到的新序列相同。從這個意義上說直接PMF處理與對M點數據先卷積后抽取的處理是相同的。因此，直接PMF的頻譜就是信號頻譜和矩形窗函數頻譜相乘的結果。而矩形窗的主瓣較窄，旁瓣較高且衰減較小，因此要降低扇形衰減效應，一個有效的方法就是使窗函數的主瓣寬度變寬。要使窗函數的主瓣寬度變寬，一種方法是減小矩形窗時域的窗口寬度，即減小L，但L減小N(N=M/L)隨之增大，FFT的運算量隨之增加。另一種方法是在不減小L的情況下，使用主瓣寬度較寬的窗函數。凱澤窗［11］作為一種窗函數，它的主瓣寬度較寬，旁瓣峰值較小且衰減很快，更為重要的是凱澤窗有一個可調參數β，通過調整參數β可使函數頻譜主瓣在不同寬度間變換，從而適應不同的環境，本文即采用凱澤窗進行加權。

凱澤窗與數據卷積的結果為

式中:h(n)為凱澤窗，對式(7)以抽取率L抽取可得

令k=n+Li，于是式(6)變為

凱澤窗加權PMF-FFT算法與直接PMF-FFT算法不同之處在于進行PMF時，每L點數據先與長度為L的凱澤窗相乘后再求和。由于凱澤窗的主瓣寬度較寬，在相同峰值衰減時的帶寬較寬，所允許的積分累加時間較長，PMF后可使數據進一步變短，從而減少FFT的運算量。而在相同PMF積分時間，即相同帶寬時，凱澤窗主瓣衰減較小，能夠有效降低FFT輸出的峰值衰減。另一方面，凱澤窗旁瓣峰值較小，旁瓣譜峰衰減速度很快，因此能夠有效減小頻譜泄漏。最后，凱澤窗有一個可調參數β，通過調整β可以產生主瓣寬度不同的窗，從而適應不同的環境。凱澤窗的以上特性表明，凱澤窗加權PMF-FFT的算法更有利于信噪比較低的擴頻信號的捕獲。

當本地碼相位與輸入信號碼相位一致時，二者相乘后的信號為 x(n)=ej2πfdTsn，由式(8)可得凱澤窗加權PMF-FFT的歸一化幅頻響應為

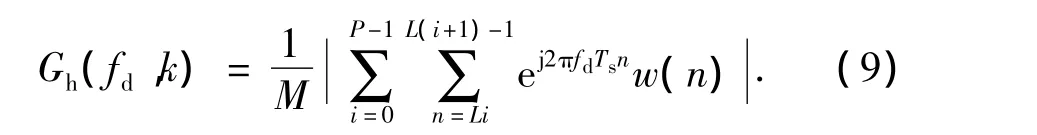
將式(6)代入式(9)中，即可得到凱澤加權的PMF-FFT的歸一化幅頻響應。圖3所示為直接PMF-FFT和凱澤窗加權PMF-FFT的歸一化幅頻響應曲線，其中實線表示凱澤窗加權的PMF-FFT算法的幅頻響應，虛線表示直接PMF-FFT的幅頻響應。

圖3 直接FFT與凱澤加權幅頻輸出比較Fig.3 Output comparison between amplitude ＆frequency about FFT and Kaiser FFT

(2)仿真與分析

采用Matlab對混合擴頻信號的捕獲進行仿真，比較直接PMF-FFT和凱澤加權的PMF-FFT對捕獲的相關峰幅度的影響。

仿真條件:跳頻16個頻點，每個跳頻間隙調制16個直擴偽碼周期，跳頻速率500 hop/s;直擴碼為Gold碼，碼長511，碼速率4.088 Mchip/s，采樣率56 MHz;多普勒頻偏設置為150 kHz，碼相位設置偏移2 610;L長度為50，FFT點數為512;β=7.865。

設載噪比范圍為46～55 dB·Hz，分別仿真2種方法在不同載噪比下捕獲時的峰值幅度。從圖4中可以看出，當載噪比升高時，峰值幅度均有緩慢的下降，其原因是帶內高斯白噪聲的減小，減小了相關峰的幅值。相同載噪比下凱澤加窗的峰值幅度至少要大于直接PMF-FFT的峰值幅度120，說明凱澤加權后對幅值改善效果明顯。

圖4 不同載噪比下直接PMF與凱澤加權下的幅度比較Fig.4 Scope comparison between FFT to Kaiser window weighted PMF in different C/N

2.3 對柵欄效應的改進

(1)改進的原理

從2.1分析中可知，采用PMF-FFT方法時若fd不是FFT頻率分辨率的整數倍時，此時fd是位于FFT主瓣內2條最大譜線(m，m+1)之間，可表示為

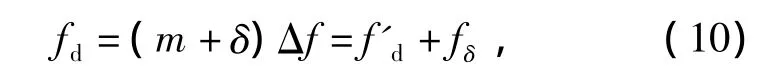
式中:f'd為對fd的估計值;m為離正確多普勒最近的整數值;fδ為正確多普勒頻率與估計值之間的相對偏差。參數設置與2.1相同，則經PMF-FFT后頻率分辨率為fs/L/512=2.187 5 kHz，也就是說當fd位于FFT輸出兩點之間時，會有較大的誤差。因此可以通過插值的方法來估計多普勒頻偏，對刪欄效應加以改進［12］。

在插值方法中，拋物線插值法運算量小，精度較高，適合于混合擴頻信號快速捕獲需要。拋物線插值法是基于3個已知點的估計法，利用FFT頻譜峰值和其左右相鄰兩個點可提高譜峰的估計精度。

拋物線插值法為首先建立一個二次插值多項式:y=ax2+bx+c，其中 a，b，c均為系數。假設已知直接FFT估計的峰值點及左右兩點的采樣值分別為(x0，y0)，(x1，y1)，(x2，y2)，真正的頻譜峰值點為(x，y)，如圖5。

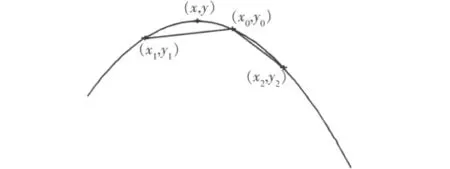
圖5 拋物線估計原理圖Fig.5 Theory figure about the estimate of parabola arithmetic

將已知點帶入式(10)并聯立可得

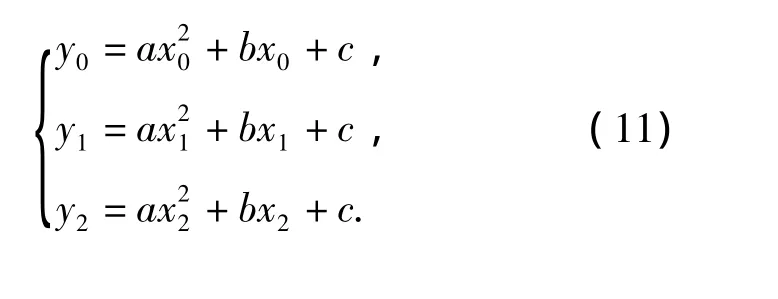
解方程組可得

當多普勒頻率位于整數倍頻率分辨率時，y1=y2，此時直接FFT法和拋物線插值法估計的多普勒相等，都等于實際的多普勒頻偏，此時估計的誤差也最小。當多普勒頻偏位于2個整數倍頻率分辨率正中時，y1=y0或y2=y0，此時直接FFT法的頻率估計誤差為頻率分辨率的一半，估計誤差最大;而拋物線插值法修正的峰點為y0-0.5，當y1=y0時或是y0+0.5，當y2=y0，與實際值相當，頻率估計誤差也最小。所以，只需知道直接FFT估計的峰值點及其左右兩點幅值、各幅度對應的頻域采樣點位置，就可以進一步精確估計出多普勒的頻偏。

(2)仿真與分析

仿真條件:與2.2中相同。

1)設輸入信號的多普勒頻率變化范圍為145～150 kHz，步進為 100 kHz，載噪比為 59 dB·Hz，直接FFT法頻率的分辨率為2 187.5 Hz，仿真1 000次取統計平均。仿真結果如圖6a)所示。

2)設定多普勒頻率為148 kHz，載噪比變化范圍為49～59 dB·Hz，高斯帶通白噪聲，每個載噪比仿真1 000次，取統計平均。仿真結果如圖6b)所示。

圖6 有無插值法估計頻差比較Fig.6 Estimate error comparison of frequency in with or without parabola arithmetic

從圖6a)中可以看出，直接FFT法和拋物線插值法對頻率估計的誤差與理論分析的結果一致。當多普勒頻率位于FFT輸出的兩點中間時估計誤差最大，從兩點中間向兩邊越接近整數倍頻率分辨率誤差越小，而位于頻率分辨率整數倍時估計誤差最小。拋物線插值法位于整數倍分辨率或是位于整數倍分辨率中間時誤差均較小，其他位置則有上下的波動，但總的誤差比FFT直接估計法的要小，誤差變化在±60 Hz內，有效改善了FFT直接估計法估計精度不高的問題，有利于后繼部分快速地跟蹤。

圖6b)為2種不同算法在載噪比變化的情況下多普勒的估計誤差。從圖中可以看出，隨著載噪比的增大，2種方法對多普勒頻偏的估計精度都有所提高，而拋物線插值法的估計精度在同載噪比下要高于FFT直接估計法。由于噪聲的影響，在低信噪的條件下，拋物線插值法對頻率估計的改善要略低于高信噪比的情況。

3 結束語

針對航天測控信號捕獲時面臨的大的多普勒頻移、后繼有跟蹤需求以及接收信號信噪比低的特點，采用快速掃描法與PMF-FFT的方法來實現對混合擴頻測控信號的捕獲。本文提出了基于凱澤窗PMF-FFT的改進算法，充分利用了凱澤窗函數主瓣寬度較寬，峰值衰減較小，旁瓣峰值低，衰減較快特性，增大捕獲時頻譜幅值峰度，因此，凱澤窗加權PMF-FFT算法和直接PMF-FFT算法相比具有明顯的優勢。而基于拋物線法測頻利用3個已知頻點對正確頻率值進行估計，算法簡單，運算量小，與不采取拋物線測頻法相比估計精度有很大提高，測頻誤差的減小有利于后繼跟蹤的快速建立。

［1］ 趙曙光，楊莘元，盧鑫.航天測控通信系統中的高速數據傳輸技術［J］.飛行器測控學報，2003，22(1):41-44.ZHAO Shu-guang，YANG Xin-yuan，LU Xin.High-Speed Data Transmission Technology in TT＆C Telecommunication［J］.Journal of Spacecraft TT＆C Technology，2003，22(1):41-44.

［2］ 成躍進，周宇昌.軍用通信衛星與信息戰［J］.空間電子技術，2001(1/2):15-29.CHENG yue-jin，ZHOU yu-chang.Military Communication Satellite and Information Warfare［J］.Space Electronics，2001(1/2):15-29.

［3］ 楊文革，文貽軍，孟生云，等.一種直擴/跳頻混和擴頻信號測量性能分析［J］.電訊技術，2009，49(1):13-17.YANG Wen-ge，WEN Yi-jun，MENG Sheng-yun，et al.Performance Analysis of a Kind of DS/FH Hybrid Spread Spectrum Signal for Telemetry［J］.Telecommunication Engineering，2009，49(1):13-17.

［4］ 李超，徐友云，羅漢文，等.DS/FH混合擴頻通信系統雙級同步技術研究［J］.移動通信，2004(增):50-53.LI Chao，XU You-yun，LUO Han-wen，et al.A Study of Double Stage Synchronization of DS/FH Hybrid Spread Spectrum Communications System［J］.Mobile Communications，2004(z1):50-53.

［5］ 劉繼承，李暑堅，邵定蓉.基于編碼擴頻的DS/FH混合擴頻通信系統同步與數據解調技術的研究［J］.遙測遙控，2002，23(5):29-34.LIU Ji-cheng，LI Shu-jian，SHAO Ding-rong.Study on Synchronization and Data Demodulation of Hybrid DS/FH System Based on Coding Spread Spectrum［J］.Journal of Telemetry，Tracking，and Command，2002，23(5):29-34.

［6］ 張波，邵定蓉，李署堅.DS/FH混合系統快速同步的研究［J］.北京航空航天大學學報，2005，31(11):1226-1231.ZHANG Bo，SHAO Ding-rong，LI Shu-jian.Study on Fast Synchronization of Hybrid DS/FH System［J］.Journal of Beijing University of Aeronatics and Astronautics，2005，31(11):1226-1231.

［7］ 孟生云，楊文革，王金寶，等.DS/FH擴頻測控信號同步方案的捕獲性能［J］.宇航學報，2010，31(8):2036-2041.MENG Sheng-yun，YANG Wen-ge，WANG Jin-bao，et al.Acquisition Performance of a Synchronization Scheme of DS/FH Spread Spectrum TTC Signals［J］.Journal of Astronautics，31(8):2036-2041.

［8］ 王燕.衛星通信鏈路(四)典型鏈路中的鏈路損耗［J］. 國際電子戰，2005(8):52-53.WANG Yan.Satellite Communication Link(4)A Typical Link in the Link Loss［J］.Iinternational Electronic Warefare，2005(8):52-53.

［9］ 章蘭英.基于虛擬無線電的擴頻測控信號處理關鍵技術研究［D］.北京:裝備指揮技術學院，2010:31-33.ZHANG Lan-ying.Study on Key Technology of Spread Spectrum TT＆C Signal Processing Based on Virtual Radio［D］.Beijing:The Academy of Equipment Command＆ Technology，2010:31-33.

［10］ 郭肅麗，劉云飛.一種基于FFT的偽碼快捕方法［J］.無線電通信技術，2003，29(1):11-13.GUO Su-li，LIU Yun-fei.A Based FFT Method of Fast Acquired Pseudo Coad［J］.Radio Communications Technology，2003，29(1):11-13.

［11］ 奧本海姆A V，謝弗R W，巴克J R.離散時間信號處理［M］.黃建國，劉海棠，譯.北京:科學出版社，1998:374-379.OPPENHEIM A V，SCHAEFER R W，BUCK J R.Discrete-Time Signal Processing［M］.HUANG jian-guo，LIU hai-tang，Translate.Beijing:Science Press，2001:374-379.

［12］ 封建湖，車剛明，聶玉峰.數值分析原理［M］.北京:科學技術出版社，2001:17-19.FENG Jian-hu，CHE Gang-ming，NIE Yu-feng.The Principle of Numerical Analysis［M］.Beijing:Science and Technology Press 2001:17-19.