基于貪婪算法的貨位優化模型
劉志帥,仝凌云,魏利鵬,朱 凱,茜曉立
LIU Zhi-shuai1,TONG Ling-yun1,WEI Li-peng2,ZHU Kai1,QIAN Xiao-li1
(1.河北工業大學 經濟管理學院,天津 300401;2.天津理工大學 中環信息學院,天津 300380)
(1.School of Economics&Management,Hebei University of Technology,Tianjin 300401,China;2.Zhonghuan Information College,Tianjin University of Technology,Tianjin 300380,China)
伴隨科技的進步和經濟的發展,尤其是改革開放以來,我國倉儲業取得了快速發展,倉儲設施得到明顯改善,服務水平與作業效率有所提高。但從總體上看,我國倉儲業的傳統經營方式還沒有根本性改變,倉儲自動化、標準化與信息化管理仍處于較低水平,造成我國流通企業商品庫存時間過長、占壓資金過多。2007至2011年,我國總物流費用占國內生產總值的比重由18.2%下降到17.8%,而保管費用占國內生產總值的比重卻由5.8%上升到6.1%[1]。企業往往從運營成本角度考慮,導致依賴人工作業的倉庫和配送中心仍占據較大比重。
倉庫和配送中心作為供應鏈的一個重要組成部分,其訂單揀選作業系統的效率是影響倉庫和配送中心整體運行效率的關鍵因素,進而也影響整個供應鏈的運營效率。倉庫或配送中心大約50%~75%運營成本都來源于訂單揀選作業[2]。訂單揀選作業是倉儲工作人員根據顧客訂單在貨位上揀取貨品的整個作業流程,其效率的高低受到貨位布局和企業運營策略的影響。而通過貨位優化可以改善訂單揀選作業的效率。
當前,國內外學者貨位優化的研究較多,主要集中在以一段時期內的訂單揀選作業成本最小、訂單揀選時間最小、行走距離最短、貨架重心最低等為目標建立相關的貨位優化模型研究方面,較少考慮到貨品特性中的質量對訂單揀選作業影響。從人因工程學的角度來考慮,在實際的訂單揀選作業過程中,貨品質量也是影響搬運效率的重要因素之一,尤其是完全依賴人工作業的倉庫或配送中心。
基于分類存儲策略,本文通過對一段時期內的有效訂單進行統計,以人工訂單揀選作業導致的人體能耗最小為目標,建立了貨位優化模型,然后利用貪婪算法對該數學模型較為快速地進行求解。
1 貨位優化模型
1.1 分類存儲策略
存儲策略即決定貨品在倉庫或配送中心存儲區域位置的指派方法及相關原則,合適的存儲策略可以減少出入庫移動的距離、縮短作業時間,甚至能夠充分利用存儲空間。常見的存儲策略有固定貨位存儲策略、隨機存儲策略、分類存儲策略、分類隨機存儲策略和共同存儲策略。其中分類存儲策略是指把貨品按照類別進行存儲,并且每一類別的貨物都有其固定的存儲區域,而同屬一類的不同貨品又按照一定的原則來指定貨位。分類存儲策略方便暢銷貨品的存取,具有固定貨位存儲策略的所有優點[3]。故本文選用其作為存儲策略,考慮如何將倉庫或配送中心的貨位安排給各個分類,最終實現人工訂單揀選作業所致的人體能耗的最小化。
1.2 貨位優化模型假設
為了構建貨位優化數學模型,提出以下假設:
倉庫或配送中心只有一個出入口;同一貨位僅存儲同一類別貨品,不允許混放;同一類別貨品可以有多個貨位;每個貨位存放的貨品以容積為限;所有貨位及托盤尺寸一致;訂單揀選作業人員勻速行走;訂單揀選作業人員人體能耗只由貨品質量引起,工作人員自身質量和揀選設備質量不計,且只計算在貨位至出庫口的克服摩擦力導致的能耗,不計從貨位揀取至設備上的人體能耗;訂單揀選作業揀取貨品的貨位始終為該類別貨品距離出口最近的貨位;貨位至出庫口的距離采用直線距離(曼哈頓距離)計算。
1.3 建立模型
設置優化模型參數如下:
Hi——第i類貨品,1≤i≤I
Hij——第i類中的第j種貨品,1≤i≤I,1≤j≤J
Qm——第m個貨區,1≤m≤M
Qmn——第m貨區中的第n個貨位,1≤m≤M,1≤n≤N
Lmn——第m貨區的第n個貨位至出庫口平面直線距離,1≤m≤M,1≤n≤N
μ——搬運設備與倉庫或配送中心地面的摩擦系數
mij——第i類中的第j種貨品的單件質量,1≤i≤I,1≤j≤J
nij——第i類中的第j種貨品的出貨數量,1≤i≤I,1≤j≤J
Mij——第i類中的第j種貨品的總出貨質量,1≤i≤I,1≤j≤J——第i類貨品的總出貨質量,1≤i≤I,1≤j≤J
XHiQm——表示若第i類貨品存儲在第m貨區中,則XHiQm=1,否則 XHiQm=0,1≤i≤I,1≤m≤M
XHijQmm——表示若第i類中的第j種貨品存儲在第m貨區中的第n個貨位中,則XHijQmn=1,否則XHijQmn=0,1≤i≤I,1≤j≤J,1≤m≤M,1≤n≤N
以任意某一段時期內的有效訂單為研究對象,結合物理學相關知識,訂單揀選作業導致的人體能量消耗主要來自于克服搬運設備與地面摩擦力,從貨位Qmn揀取貨品Hij的人體能耗,則可以表示為:
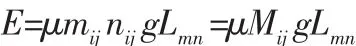
其中,g為重力加速度,取9.8N/kg,其他計量單位均為相對應的國際標準單位。
因此,可得到目標函數:
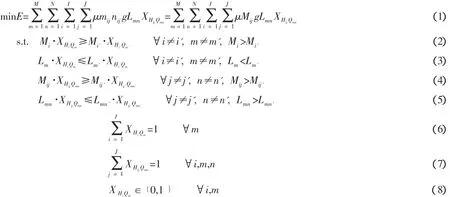

其中,目標函數(1)表示貨位優化之后,使得人工訂單揀選作業所導致的人體能耗最小;約束條件(2)和(3)保證把總出貨質量較大的貨品類指派到距離出口較近的貨區中;約束條件(4)和(5)確保把同一類中總出貨質量較大的貨品種別指派到距離出口較近的貨位上;約束條件(6)表示貨區存儲的唯一性,即貨區Qm僅存儲同一類別的貨品;約束條件(7)表示貨位存儲的唯一性,即貨位Qmn僅存儲一種貨品品項;約束條件(8)和(9)為決策變量的取值約束;約束條件(10)表示貨區數目和貨品類別數目必須一致。
2 貪婪算法求解模型
2.1 貪婪算法
貪婪算法(又稱貪心算法)是一種常用的求解最優化問題的簡單、迅速的方法。在求解問題時,貪婪算法總是做出在當前看來最好的選擇,它所作的每一個選擇都是在當前狀態下某種意義的最好選擇即貪心選擇,并希望通過每次所作的貪心選擇導致最終得到問題最優解[4-5]。其基本思路為:從問題的某一個初始解出發逐步逼近給定的目標,以盡可能快地求得更好的解。當達到某算法中的某一步不能再繼續前進時,算法停止[6]。貪婪算法不是對所有問題都能得到整體最優解,但對范圍相當廣泛的許多問題他能產生整體最優解或者是整體最優解的近似解。
對于企業而言,耗費大量的人力、財力和時間去求解目標函數的最優解是不經濟的,尤其是對那些出貨差異較大的倉庫和配送中心而言,因為最優解是伴隨時間而不斷變化的。因此,本文針對此類配送中心或倉庫,采用了貪婪算法進行快速求解。
2.2 模型求解
貪婪算法求解次貨位優化模型的步驟如下:
Step 1:計算每一個貨品品項的總質量Mij、每一類貨品品項的總質量Mi、每一個貨區到出口的距離的Lm和每一個貨位到出口的距離Lmn;
Step 2:將貨品類別按照Mi值降序(非增序)排列編號,設A()a為排序后的數列,其中a為順序號;
Step 3:將貨區按照Lm值升序(非降序)排列并編號,設B()b為排序后的數列,其中b為順序號;
Step 4:將具有最大Mi值的貨品類別Hi存儲在Lm值最小的貨區中,即把數列A()a中編號為1的那一類貨品指派到數列B(b)編號為1的貨區中,然后把編號為2的那一類貨品指派到數列B(b)編號為2的貨區中,重復這一過程,直到把數列A(a)中的所有類別的貨品指派完畢;
Step 5:將同一類下的貨品類別按照Mij值降序(非增序)排列編號,設C()c為排序后的數列,其中c為順序號;
Step 6:將同一貨區的貨位按照Lmn值升序(非降序)排列并編號,設D()d為排序后的數列,其中d為順序號;
Step 7:將具有最大Mij值的貨品類別Hij存儲在Lmn值最小的貨位中,即把數列C()c中編號為1的那一類貨品指派到數列D(d)編號為1的貨位中,然后把編號為2的那一類貨品指派到數列D(d)編號為2的貨位中,重復這一過程,直到把數列C(c)中的所有類別的貨品指派完畢;
Step 8:重復step5~7這一過程,直到把所有類別的貨品指派到特定的貨位中。
3 結束語
與之前的貨位優化目標函數不同,本文從人因工程學的視角,結合分類存儲策略,提出了以人工訂單揀選作業所致的人體能耗最小的目標函數,并建立了相關的貨位優化模型,最后利用貪婪算法這一快速求解算法進行求解。此模型不僅可以對不同時期具有明顯差異訂單的倉庫或配送中心的貨位進行快速優化,還因此降低了訂單揀選工作人員的勞動強度,提高了勞動效率。從而,進一步提高了倉庫或配送中心的運營效率,具有一定的實用性和實際意義。
[1]中華人民共和國商務部流通業發展司.商務部關于倉儲業轉型升級的指導意見[EB/OL].(2012-12-18)[2013-07-06].http://www.mofcom.gov.cn/article/b/g/201304/20130400075343.shtml.
[2]John J.Coyle,Edward J.Bardi,C.John Langley.The management of business logistics[M].St.Paul,MN:West Pub.,1996.
[3]田源,張文杰.倉儲規劃與管理[M].北京:清華大學出版社,2009:134-135.
[4]S.A.Curtis.The classification of greedy algorithms[J].Science of Computer Programming,2003,49:125-157.
[5]Seungmo Kang,Yanfeng Ouyang.The traveling purchaser problem with stochastic prices:Exact and approximate algorithms[J].European Journal of Operational Research,2011,209:265-272.
[6]魏英姿,趙明揚,黃雪梅,等.求解TSP問題的貪心遺傳算法[J].計算機工程,2004,30(19):19-20.

