新發艾滋病感染者治療依從性的Probit模型分析*

武漢科技大學醫學院預防醫學系(430065) 張連生 黃琴琴 劉 雷 劉 丹

新發艾滋病感染者治療依從性的Probit模型分析*

武漢科技大學醫學院預防醫學系(430065) 張連生 黃琴琴 劉 雷 劉 丹

目的 運用數學模型擬合艾滋病感染者治療依從性保持率的變動規律，為合理、適時采取干預措施提供理論依據。方法 收集某市2001－2012年新發艾滋病感染者的數據資料，運用SPSS15．0軟件進行Probit模型擬合。結果 累積新發感染者治療依從性保持率r(t)的模型為r(t)=1－Φ〔－0.865+0.733×ln(t)〕，(χ2=5.306，P=0.807)，11年中最大相對誤差僅為5.96%，擬合中位數為3.25年。結論 運用Probit建立的新發艾滋病感染者治療依從性保持率模型擬合度較好。模型顯示，該市的新發感染者在1～3年內治療依從性保持率的變化幅度很大，在此之后變化幅度減小。對新發感染者要在檢測陽性結果的前3年采取主動有效干預措施，可較好地避免感染者流失。

治療依從性 感染者保持率 Probit模型

提高艾滋病感染者治療依從性直接關系該病的治療效果。AIDs病人按照要求合理服用抗病毒藥，接受規范的抗病毒治療是提高艾滋病抗病毒治療效果，減少耐藥性發生的重要前提。目前，對HIV感染者和艾滋病患者的臨床實踐多采用以家庭和社區為基礎的綜合治療策略，即開展逆轉錄病毒藥物治療(antiretroviral therapy，ART)、預防和治療機會性感染、增強機體免疫功能、輔以支持療法及心理咨詢，其中以ART最為關鍵。研究顯示，接受ART患者的良好依從性可以保持體內藥物濃度的穩定，最大程度和持續性地抑制病毒復制，減少病毒耐藥性的出現，促進免疫重建，從而達到預期療效，減緩HIV感染發展到艾滋病的進程和減低死亡率〔1－2〕。

在發達國家和發展中國家已開展的有關ART依從性及其影響因素的研究發現，不同研究人群和不同測量方法得到的依從性水平為37%至83%〔3〕。治療依從行為是個復雜的動態過程，接受ART的患者常面臨多種因素的影響，依從性水平隨時間的推移而發生改變。對于艾滋病感染者治療依從性保持率的動態模型還缺乏相應的研究。

客戶保持率理論和數學模型

1.顧客終生價值理論和數學模型

管理學中使用顧客終生價值(CLV)來反映客戶對企業的忠實程度。客戶保持率是用來描述永久性流失客戶模型中客戶在將來交易可能性的參數，以r(t，t+1)表示客戶在［t+1］時段上的條件客戶保持率，即該客戶在時段［0，t］為保留客戶的前提下在［t，t+1］時段上繼續保留的概率。以r(t)表示客戶在時刻t的累積客戶保持率，指該客戶在成為企業的客戶后經過時段t后在t時刻仍然是企業客戶的概率。累積客戶保持率可以表示為客戶在該時刻之前的所有交易時段上的條件客戶保持率的乘積。

顧客收益函數曲線描述了整個持續期顧客終生價值的發展走向，永久性流失的典型客戶關系收益函數如下:

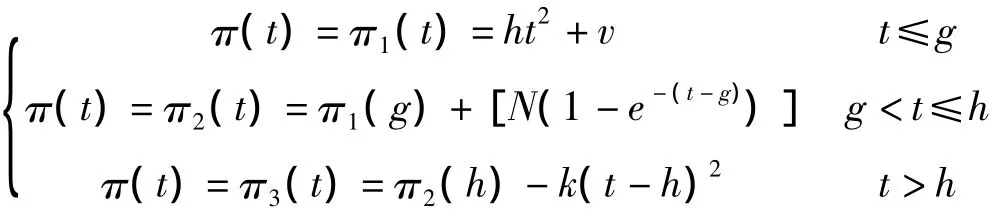
在客戶關系初期，客戶收益快速增長，在某一點g后增長速度開始逐漸變緩，到達h點后雙方關系逐漸開始走向解體，直至最后降為0。用收益現值法構建客戶終生價值模型為:

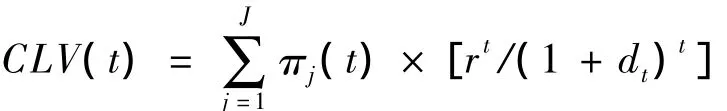
其中，d為折現率，r為顧客保持率，CLV為顧客終生價值。在顧客終生價值模型中非常重要的一個參數是累積顧客保持率r，指從成為企業的顧客后到t時刻仍然是該企業顧客的概率。

2.客戶保持率模型研究現狀

目前用于累積客戶保持率估計的常用方法是常量條件客戶保持率，即累積客戶保持率為常量指數壽命模型r(t)=bt，在 Berger和 Nada〔4〕關于客戶終生價值模型計算中涉及到的客戶累積保持率參數都采用了常量指數壽命模型。該模型假定客戶在各個交易期的條件保持率與客戶關系時間無關，是一個固定的量，在實際計算時取歷史平均條件客戶保持率。在該假定之下，客戶在交易時段的交易可能行為，即客戶的累積保持率為。

客戶流失率通常是單調遞減并且遞減幅度越來越小，這一變化導致條件客戶保持率單調遞增，但累積客戶保持率呈單調遞減，不過遞減的幅度越來越小。累積客戶保持率的指數壽命分布模型假定條件客戶保持率為常量，因此指數壽命分布模型并不能涵蓋客戶流失的所有情形，有必要尋求一種新的壽命分布模型來更好地描述客戶流失的各種情況。

齊佳音〔5〕認為威布爾壽命分布模型能夠更有效地擬合客戶流失的各種情況，通過建立威布爾生存函數，r(t)=e［－(at)b］(t＞ 0)，估計參數后得到累積顧客保持率計算模型。當r(t)=0.5時，即為累積顧客保持率下降到50%時所經歷的時間段，求出t即為該客戶群典型顧客的平均生命周期值，證實其較指數壽命分布模型有更好的擬合效果。鄭浩等〔6－7〕通過建立壽命表，得到實際的累積生存率曲線，然后計算中位數得到顧客的平均生命周期，也達到較好的結果。而這兩種模型均為冪函數，遠期地累積保持率擬合誤差較大。

艾滋病感染者治療依從性分布規律是否符合顧客保持率數學模型，本文以某市近10年艾滋病新發感染者數據，運用Probit建立模型并進行擬合。

累積保持率的Probit模型

Probit模型為概率單位模型，常用來分析某事件的發生概率受另一因素變化的影響，模型形式為:

其中，βχ稱為概率密度函數值，服從標準正態分布，Φ為累積標準正態分布函數。該模型建立在正態分布的理論基礎上，對該模型構建似然函數:

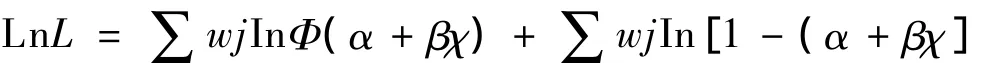
然后采用極大似然法可求解參數α、β。

在Probit模型中，要求概率p逐漸累積增大，而本文中累積顧客保持率是逐漸減少，因此在模型中，定義p為累積顧客流失率，則1－p為累積顧客保持率，得到累積顧客保持率的模型:

由于累積顧客流失率p與時間t之間一般為長尾S型曲線，對t取自然對數使曲線變換為對稱S型。

新發艾滋病感染者治療依從性累積保持率的估計分析

本文采用某市2000－2011年690名新發艾滋病感染者的治療依從性案例數據，運用SPSS15.0軟件建立Probit模型，分析新發艾滋病感染者治療依從性累積流失率和保持率的變化，結果見表1。

將表1數據進行變換處理，轉化為表2。表2中艾滋病感染者數指隨訪時間達到某一持續時間段t的數量，以9年段為例，該時段包含從2001－2009，2002－2010，2003－2011這三個時間段內被隨訪的感染者數，包括2001年的新發現艾滋病感染者，2002年的新發現艾滋病感染者，2003年的新發現艾滋病感染者，即106+27+39=172。而累積保留艾滋病感染者數指在隨訪時間段t內連續治療的感染者數量之和，以9年為例，分別經歷了這三個時間段內被隨訪的感染者數，即29+4+3=36。艾滋病感染者累積保留率=36/172×100%=20.93%;艾滋病感染者累積流失率=(172－36)/172×100%=79.07%。

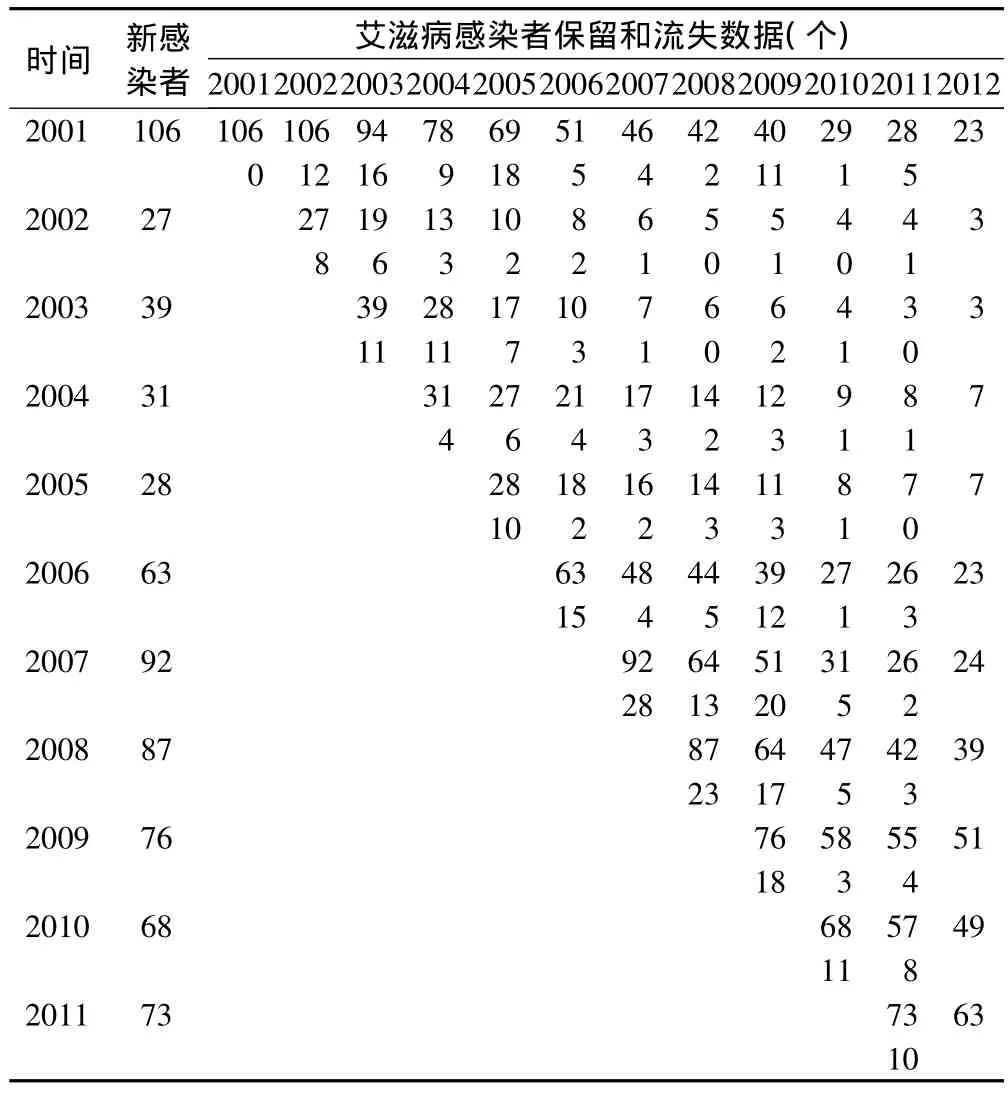
表1 某市2001～2012年艾滋病感染者保留和流失數據

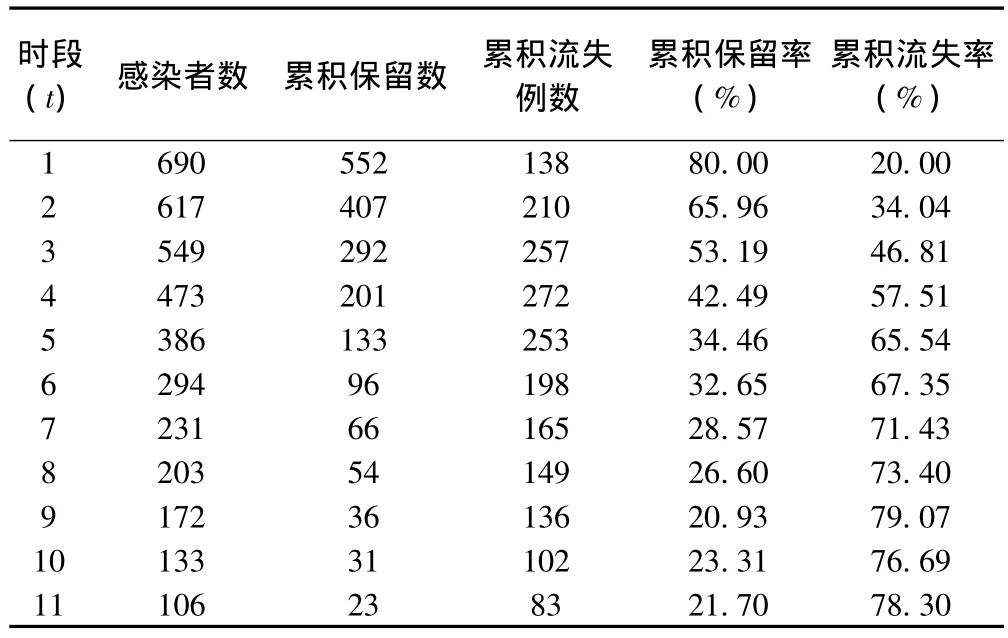
表2 某市艾滋病感染者保留和流失情況分析表

建立時刻t的自然對數ln(t)和累積流失率的Probit模型如下:

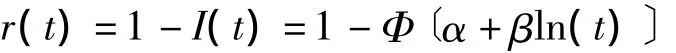
經過軟件擬合，得出某市新發艾滋病感染者治療依從性累積流失率I的模型如下:

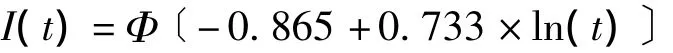
α的Se為 0.043，Z值為 －20.281;β的Se為0.030，Z值為24.243。

模型擬合較好(χ2=5.306，P=0.807。)，對應的艾滋病感染者治療依從性累積保持率r(t)的模型為:

Probit模型估計效果分析

為了對比分析新發艾滋病感染者治療依從性累積保持率的Prohit模型估計效果，對艾滋病感染者治療依從性累積保持率的Probit模型進行擬合估算，并與實際艾滋病感染者治療依從性累積保持率進行比較分析，見表3。由估計精度看，Probit模型的估計效果好。

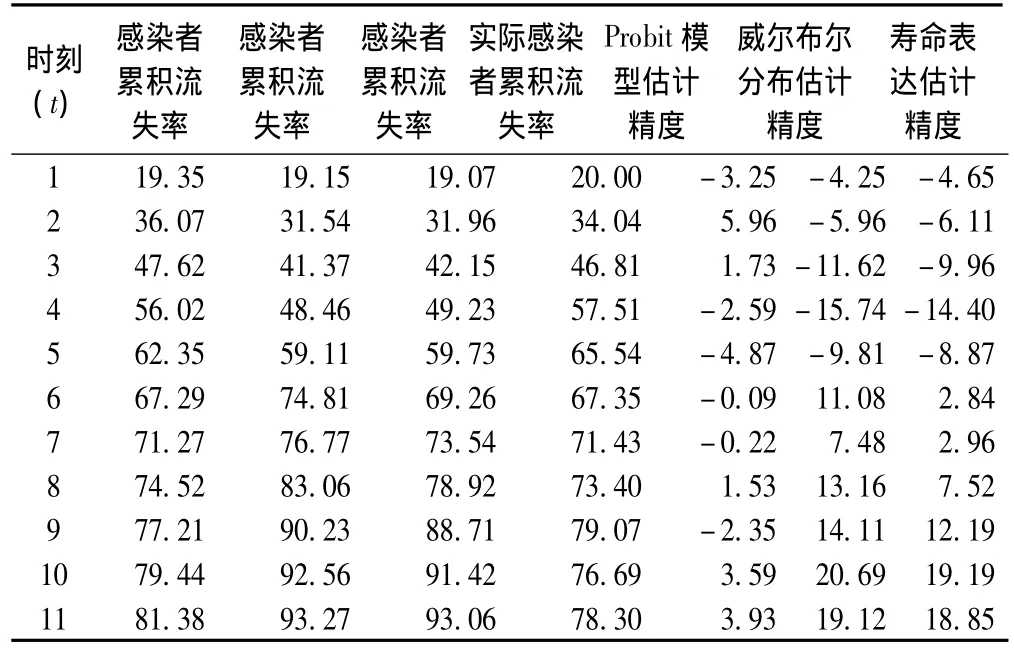
表3 感染者累積流失率的效果分析

由Probit模型進一步估計出該市的新發艾滋病感染者治療依從性累積流失率與所需時間的關系，見表4。

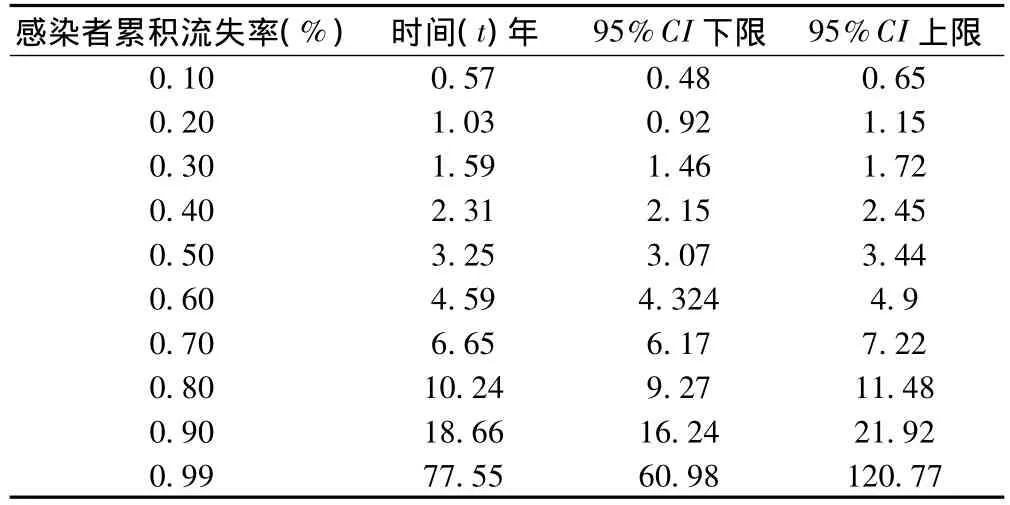
表4 感染者累積流失率與時間t的關系

由表可以查知，Probit模型的新發感染者治療依從性流失率估計中位數為3.25年，即經過3年3個月后，該市艾滋病感染者將有50%會流失。

討 論

艾滋病患者的服藥依從性對保證抗病毒藥物療效有著重要的意義。建立有效的艾滋病感染者治療依從性累積保持率模型可以降低估算的誤差，從而為醫療機構合理利用衛生資源，采用可行干預方案提供可靠的決策依據。

一般來說，艾滋病感染者在檢出艾滋病毒后的隨訪早期，有較高的流失率，隨著時間的推移，對醫療機構的依從性逐步形成，關系時間越長久的感染者越容易保留下來，累積保留率逐漸以較小的幅度減少。該市的新發艾滋病感染者治療依從性數據明顯地呈現這一趨勢，在1～3年之前新發艾滋病感染者保持率的變化幅度很大，在此之后變化幅度減小。依從性影響因素可分為四類:患者相關因素，如社會人口學和心理學因素、個人技能等;醫療服務質量和醫患關系;與治療方案或藥物副作用相關因素，如治療方案、抗HIV藥物的副作用、治療時間的長短等;社會環境因素，如衛生保健服務、家庭關懷和社會支持、醫療實踐括動等。

本文運用Probit模型給出了計算疾病治療依從性累積保持率的一種新方法，研究結果表明，Probit模型可以較為地準確描述新發艾滋病感染者治療依從性流失率的變化情況，從而能更客觀地確定艾滋病感染者治療依從性累積保持率，是衛生部門依據艾滋病感染者治療依從性保持率進行治療依從性決策的理論基礎。

1．Li H，Li L，et al．Prevalence and evolution of drug resistance HIV-1 variants in Henan，China Cell Research，2005，15:843-849．

2．錢峰，呂效國．多目標優化模型在艾滋瘸療法的療效預測上的應用．中國衛生統計，2009，26(1):101-102．

3．Simoni J，Frick P，Patalone D，et a1．Antiretroviral adherence interventions:a review of current literature and ongoing studies．Topics in HIV Medicine，2003，11(6):185-198．

4．Berger P，Nada I．Customer lifetime value:Marketing model and applications ．Journal of Interactive Marketing，1998，12(1):17-30．

5．齊佳音，車懷祖，舒牟美．一種新的累積客戶保持率模型．管理工程學報，2004，(4):150-155．

6．鄭浩．顧客終生價值預測中顧客生命周期參數的確定．統計與決策，2006(20):152-154．

7．葉勇．基于Probit模型的客戶累積保持率分析．統計與決策，2007(14):161-163．

Probit Model for the New AIDS Infestors Treatment Compli-ance

Zhang Liansheng，Huang Qinqin，Liu Lei，et al．Medical College，Wuhan University of Science ＆ Technology(430065)，Wuhan

ObjectiveTo study the altering regularity of the maintaining rate of treatment compliance of the new AIDs infestors with mathematical model，in order to provide theoretical evidence for reasonable and timely interventions.MethodsThe data of the new AIDs infestors was collected from 2001 to 2012 in a certain city．The Probit model was used to analysis the new AIDs infestors cumulative maintaining rate by using SPSS15.0 software.ResultsThe model of the new AIDs infestors cumulative maintaining rate is r(t)=1－Φ〔－0.865+0.733×In(t)〕，χ2=5.306，P=0.807，the maximum error of 11year is as low as 5.96%sonly 5.96%，and the estimated fitting median is 3.25years)．Conclusion The model of new AIDs infestors cumulative maintaining rate fits well．It indicates the amplitude of the new AIDs infestors cumulative maintaining rate changes remarkably in the first three years．Afterwards，the change in amplitude reduces．For the new AIDs infestors，the activeness intervention measures are adopted in the first three years，so to avoid the loss for infestors．Given active interventions are meted out for the new AIDs infectors，the loss of infectors could be avoided effectively．

Treatment compliance;Infestor maintaining rate of treatment compliance;Probit model

湖北省人文社科重點研究基地——湖北非營利組織研究中心項目(HBNP02012ZD003)

(責任編輯:劉 壯)