彈性復合圓柱滾子軸承靜態徑向剛度分析

姚齊水 張 然 明興祖 楊 文

湖南工業大學，株洲，412007

0 引言

圓柱滾子軸承因其滾動體與滾道為線接觸、徑向承載能力和徑向剛度較高的特點，廣泛應用于各類機械設備中。目前使用的圓柱滾子軸承的滾動體一般為實心圓柱滾動體（或外表面帶有一定凸度的實心圓柱滾動體）和空心圓柱滾動體（去掉實心圓柱滾動體中心部分的材料，將滾動體做成空心狀）兩種。從實際應用中發現，實心圓柱滾子軸承存在傳動精度不高、振動噪聲大、高速和重載情況下容易損壞等不足，空心圓柱滾子軸承具備較高的傳動精度和振動性能等優點，但受載空心滾動體處于周期性的交替變形狀態，空心滾動體的內壁容易彎曲疲勞斷裂，因此，研制具有高精度、高轉速、高壽命的圓柱滾子軸承在工程上具有特別重要的意義。筆者根據組合創新的原理，在保留實心圓柱滾子軸承和空心圓柱滾子軸承優點的基礎上，提出了一種全新的彈性復合圓柱滾子軸承，并申請了專利［1］。

軸承的剛度是軸承的重要參數之一，定義為軸承內外套圈產生單位的相對彈性位移量所需要的外加載荷。剛度參數對整個系統的振動、噪聲、壽命有著非常重要的影響，研究彈性復合圓柱滾子軸承的剛度十分必要。國內外許多學者對實心圓柱滾子軸承和空心圓柱滾子軸承剛度的研究做了大量工作：Harris等［2］給出了點接觸和線接觸情況下軸承的接觸應力分布和接觸變形公式；Erwin等［3］給出了計算線接觸圓柱滾子軸承彈性變形的近似公式；陳家慶等［4］利用曲梁理論推導出空心圓柱滾子軸承接觸變形公式；劉衛群等［5］利用PSARB程序編寫的程序分析了滾動軸承的剛度；李偉健等［6－7］利用當量彈性模量的分析方法推導出了空心圓柱滾子軸承的剛度計算公式。考慮到彈性復合圓柱滾子軸承結構上的特殊性，不能直接應用上述的研究結論。本文將在分析計算彈性復合圓柱滾子軸承載荷分布的基礎上，利用有限元仿真的方法計算軸承的受載變形，結合剛度的定義，推導出彈性復合圓柱滾子軸承靜態徑向剛度的計算公式；再通過彈性復合圓柱滾子軸承剛度的計算，分析填充度、外載荷、滾子數三者對彈性復合圓柱滾子軸承剛度的影響規律，并和空心圓柱滾子軸承的剛度進行比較。

1 載荷分布［8］

彈性復合圓柱滾子軸承結構如圖1所示。彈性復合圓柱滾子軸承是在空心圓柱滾子軸承的滾動體中嵌入聚四氟乙烯材料，用以改善滾動體內壁的應力狀態，減小內壁彎曲疲勞應力，提高承載性能［9］，延長軸承的安全服役壽命［8］。為了便于分析計算，作如下假設：①軸承內外圈均為剛體，不發生變形；②所有的彈性變形均發生在滾動體上；③軸承外圈靜止，內圈在外載荷作用下發生相應的位移；④滾動體和內部的填充物之間粘結良好，可看作一個整體結構。

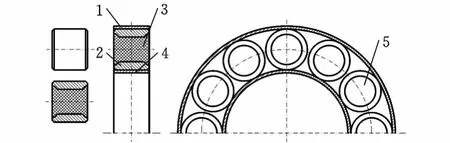
圖1 彈性復合圓柱滾子軸承結構圖

軸承在承載過程中受接觸變形等原因的影響，不同位置的滾動體所承受的載荷和彈性變形都不同，所以研究在受載情況下的載荷分布具有十分重要的意義。如圖2所示，在不考慮徑向游隙的情況下，軸承在承受徑向載荷Fr時，內圈中心從O點沿徑向移動到O′點，相對于外圈產生徑向位移δ。假設有一個滾動體的中心位于徑向負荷的作用線上，取最下面的滾動體編號為0，產生的彈性變形量為δ0（在徑向游隙為0的情況下δ0＝δ），從最下面的滾動體向兩邊依次給每個滾動體編號，則第i個滾動體上產生的理論變形量為δi。

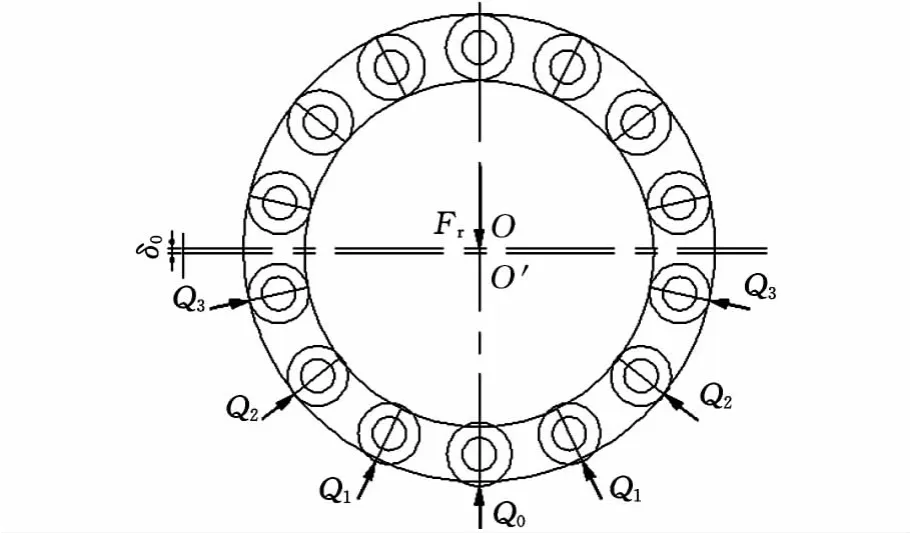
圖2 彈性復合圓柱滾子軸承受徑向載荷時的載荷分布

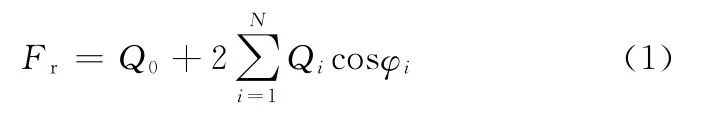
式中，φi為第i個滾動體中心和外圈中心連線與徑向負荷作用線之間的夾角；N為軸承單邊接觸滾動體數。

根據軸承整體的受力平衡可得

變形協調方程如下：

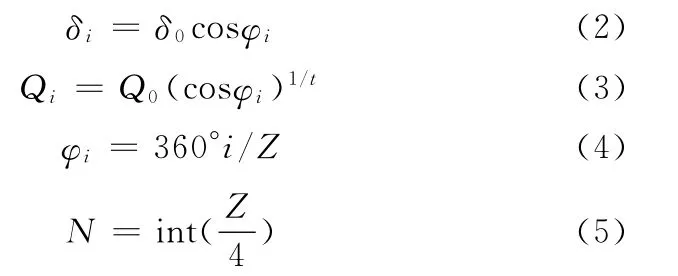
式中，Z為滾動體總數；t為指數，線接觸時，t＝0.9。

聯立式（2）～ 式（5）并且代入式（1）可求得

其中，對于圓柱滾子軸承，有

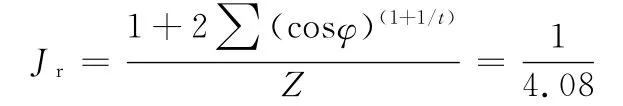
通過式（6）可求得Q0的一個初始值，再代入式（1）～ 式（5）反復進行迭代運算，求得Q0的一個精確值，最后通過式（3）可求得彈性復合圓柱滾子軸承在承受徑向載荷時每個滾動體所承受的載荷。

2 接觸變形有限元仿真計算

根據 GB／T4661－2002以及 GB／T283－2007來確定本文所要分析的彈性復合圓柱滾子軸承的各項參數，如表1所示。

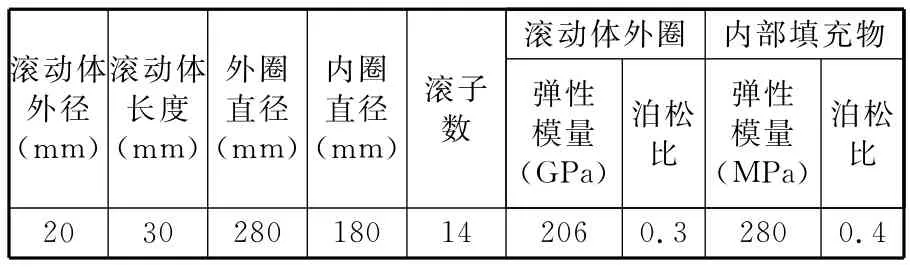
表1 彈性復合圓柱滾子軸承參數

應用ABAQUS軟件進行有限元建模，根據上述假設①和假設②，不考慮內外圈的接觸變形，利用文獻［7］中所用方法，將軸承內外圈的彈性模量設置為206TPa（該彈性模量遠大于滾動體外圈彈性模量，接觸變形可忽略），泊松比為0.3。考慮到軸承受力的對稱性和軸承的滾子數，在建立模型時，分別取1／20的軸承內外圈和1／2的滾動體進行分析，在不影響計算結果的前提下，將內圈的內表面和外圈的外表面簡化為平面。采用單元類型為三維二次完全積分單元來對模型進行網格劃分。由于滾動體與內外圈接觸區域的接觸半寬很小，容易產生應力集中，將此區域網格進行局部細劃，而內外圈基本不發生變形，對計算結果影響不大，此區域網格劃分相對較粗。在定義相互作用時，對滾動體外圈和內部填充物施加綁定約束；而滾動體和滾道之間的接觸采取面面接觸，以內外圈接觸面為主面，滾動體接觸面為從面，對內外圈與滾動體之間分別設立接觸對。有限元分析模型如圖3所示。

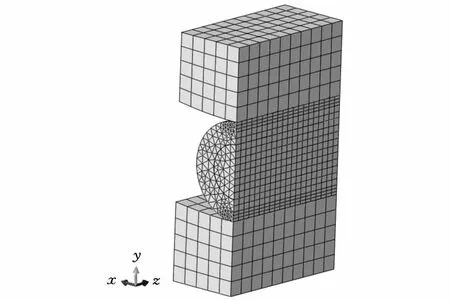
圖3 彈性復合圓柱滾動體與內外圈接觸有限元分析模型

邊界條件的設置在有限元的分析中起著非常重要的作用。工作過程中軸承外圈與軸承座之間不會發生相對轉動，可視為固定，在外圈外表面添加所有自由度的約束；在模型的剖面處施加對稱約束；在內圈的端面處施加軸向的約束。在內圈的內表面施加總和為Qi／2的均布載荷，內圈在邊界條件和徑向載荷的作用下，只能沿著y軸方向移動，而這部分位移則會被滾動體和內外圈的變形所吸收，即內圈在y軸上的位移就是滾動體所產生的徑向變形量的大小。

3 剛度計算公式

軸承的徑向剛度是指軸承內外套圈產生單位的相對彈性位移量所需的外載荷，軸承的徑向剛度等于軸承所受徑向載荷除以徑向變形，結合載荷分布公式可得

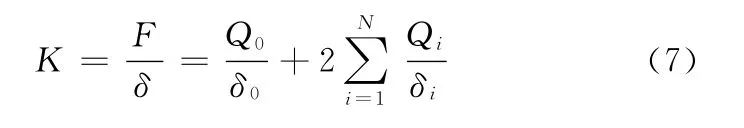
4 計算結果及分析

定義滾動體的填充度為k，k＝d／D，其中d為填充物的直徑，D為滾動體外圈的外徑。取不同徑向載荷和不同填充度的彈性復合圓柱滾子軸承，結合載荷分布公式以及彈性變形的有限元計算結果，對彈性復合圓柱滾子軸承的徑向剛度計算結果如表2所示。

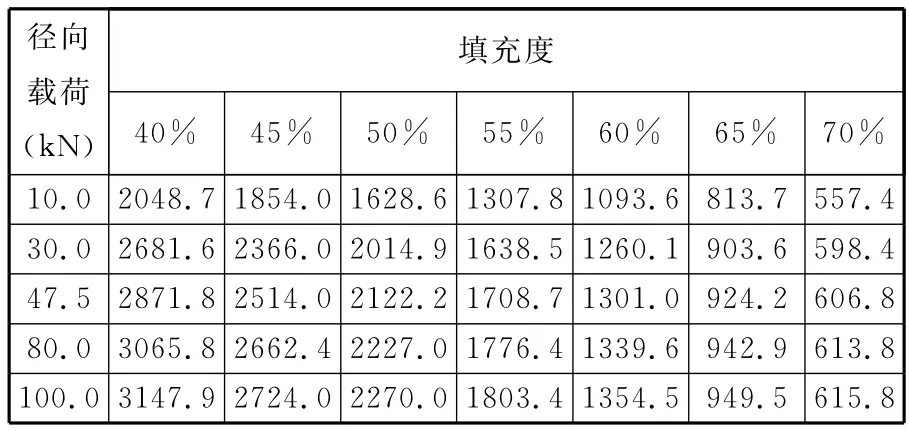
表2 不同填充度、不同載荷情況下彈性復合圓柱滾子軸承的剛度值 MN／m

4.1 填充度對剛度的影響

填充度是影響彈性復合圓柱滾子軸承剛度的一個非常重要的因素，填充度過小則對軸承的接觸狀態和變形影響不大［10］，無法體現彈性復合圓柱滾子軸承的優勢，填充度過大則容易變形過大而產生破壞，本文取填充度從40%到70%的情況來分析。為分析方便，將表2的數據進行處理，結果如圖4和圖5所示。可以看出：在相同載荷情況下，隨著滾動體填充度增大，彈性復合圓柱滾子軸承的剛度都是迅速減小的；填充度在40%到55%之間，隨著外載荷增大，軸承的剛度都有著明顯的增大趨勢；填充度在60%到70%之間，隨著載荷增大，軸承的剛度基本上變化不大，在70%時，剛度甚至趨近于一條水平線。

4.2 徑向載荷對剛度的影響

徑向載荷是另一個對軸承剛度影響很大的參素，從圖4和圖5中可以看出，徑向載荷對軸承剛度的影響是隨著填充度的不同而不同的。外載荷在30kN到100kN之間時，隨著填充度增大，軸承的剛度迅速減小；而當徑向載荷等于10kN時，隨著填充度增大，軸承的剛度減小趨勢明顯變小。徑向載荷越小，隨著載荷增大，對軸承的剛度提升就越大；徑向載荷越大，隨著載荷增大，對軸承的剛度提升幅度就越小。

圖4 軸承剛度與填充度的關系圖

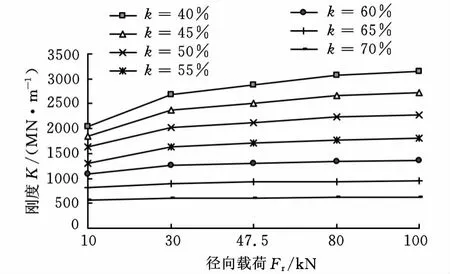
圖5 軸承剛度與徑向載荷的關系圖

4.3 滾子數對剛度的影響

由式（1）～式（6）可知，滾子數對軸承的載荷分布有著非常重要的影響，進而也影響著軸承的剛度值。表3表明，在相同外載荷和填充度的情況下，隨著滾子數增多，彈性復合圓柱滾子軸承的靜態徑向剛度逐漸增大；填充度越小，滾子數的增加對軸承的剛度提升幅度越大，填充度越大，滾子數的增加對軸承的剛度提升幅度越小。滾子數越多，隨著填充度增大，軸承的剛度減小越明顯。

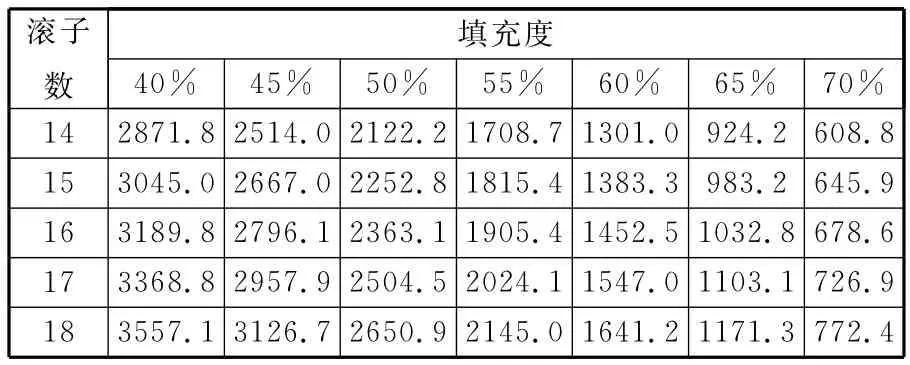
表3 Fr＝47.5kN時，不同滾子數、不同填充度情況下彈性復合圓柱滾子軸承的剛度值 MN／m

4.4 和空心圓柱滾子軸承剛度比較

從表4不難發現，相同填充度和空心度（即針對空心圓柱滾子軸承的參數）的彈性復合圓柱滾子軸承的剛度一直比空心圓柱滾子軸承大，填充度（空心度）越大，彈性復合圓柱滾子軸承和空心圓柱滾子軸承的剛度差越大。填充度為40%的彈性復合圓柱滾子軸承和空心度為40%的空心圓柱滾子軸承的剛度差小于1%，幾乎可以忽略；而填充度為70%的彈性復合圓柱滾子軸承和空心度為70%的空心圓柱滾子軸承的剛度差約為4%，已經不能夠完全忽略。這是由于在填充度較小的時候，填充度所占的體積比較小，對軸承的剛度影響不大，隨著填充度增大，填充物所占的體積比越來越大，所承受的力越來越大，對軸承的影響也就越來越大。

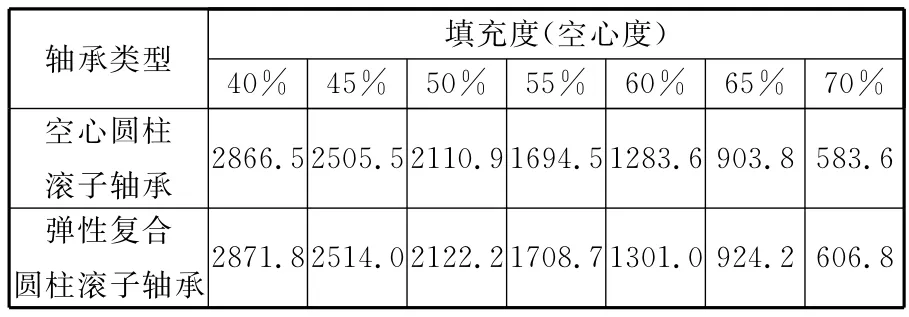
表4 Fr＝47.5kN時，彈性復合圓柱滾子軸承和空心圓柱滾子軸承的剛度值比較 MN／m

5 驗證

彈性復合圓柱滾子軸承與實心圓柱滾子軸承僅在滾子內部結構方面存在差異，兩者與內圈形成的接觸副的情況相似，可以將分析實心滾子軸承時建立的有限元模型用來分析彈性復合圓柱滾子軸承的接觸問題［11］。反之，用與上述彈性復合圓柱滾子軸承有限元分析模型相似的方法對實心圓柱滾子軸承的接觸變形進行有限元分析；分析過程中設定相同的邊界條件，模型中的內外圈材料和彈性復合圓柱滾子軸承分析時相同，實心滾動體的材料和彈性復合圓柱滾子軸承的滾動體外圈相同。有限元分析模型如圖6所示。

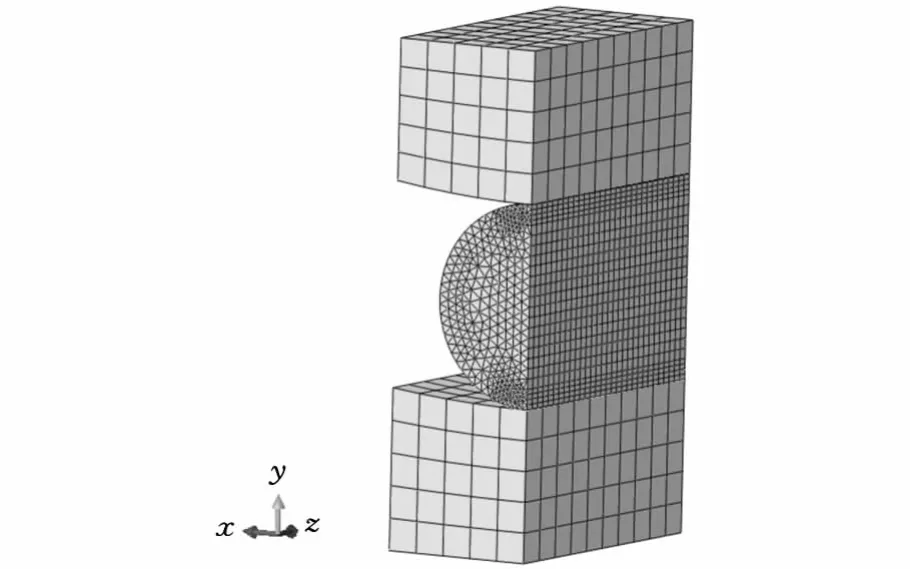
圖6 實心圓柱滾動體與內外圈接觸有限元分析模型

通過有限元計算得到了實心圓柱滾子軸承的受載變形的關系，并和帕姆格林經驗公式［3］所求得的結果進行比較，所得結果如圖7所示。

由圖7可見，本文所用的有限元計算模型在計算實心圓柱滾子軸承接觸變形時所得結果與帕姆格林理論公式所求的結果基本接近，充分說明了本文所用的有限元計算模型用于計算軸承滾動體的接觸變形是比較可靠的，求解的精度也能符合計算的標準。

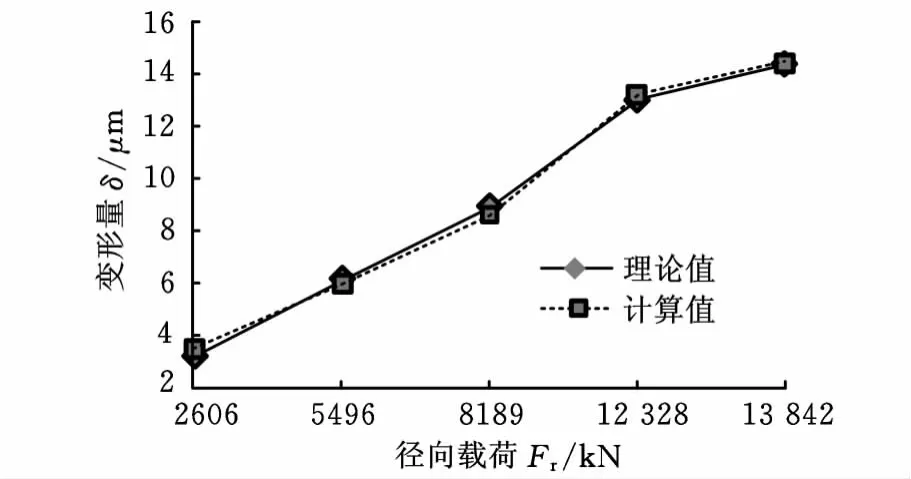
圖7 軸承實心圓柱滾子軸承接觸變形有限元計算值與理論值比較

6 結論

（1）填充度在40%到55%之間，隨著外載荷增大，軸承的剛度有著明顯的增大趨勢；填充度在60%到70%之間，隨著載荷增大，軸承的剛度基本上變化不大，填充度為70%時，軸承的剛度甚至趨近于一條水平線。

（2）外載荷較大，隨著填充度增大，軸承的剛度迅速減小；而當外載荷較小時，隨著填充度增大，軸承的剛度減小趨勢明顯變小。外載荷越小，隨著載荷增大，對軸承的剛度提升就越大；外載荷越大，隨著載荷增大，對軸承的剛度提升就越小。

（3）填充度較小的情況下，滾子數的增加對軸承的剛度提升幅度比較大；填充度較大的情況下，滾子數的增加對軸承的剛度提升幅度比較小。

（4）相同填充度和空心度的彈性復合圓柱滾子軸承的剛度一直比空心圓柱滾子軸承大，填充度（空心度）越大，彈性復合圓柱滾子軸承和空心圓柱滾子軸承的剛度差越大。

［1］姚齊水.一種彈性復合圓柱滾子軸承：中國，201120066406.1［P］.2011－11－23.

［2］Harris T A，Kotzalas M N.Advanced Concepts of Bearing Technonlogy［M］.New York：Taylor ＆Francis，2006.

［3］Erwin V，Zaretsky A.Palmgren Revisited－abasis for Bearing Life Prediction［J］.Journal of the Society of the Tnbologists and Lubrication Engineers，1998，54（2）：18－23.

［4］陳家慶，毛紅兵，張寶生.無預載荷空心圓柱滾子軸承的理論研究［J］.軸承，2002（6）：1－5.Chen Jiaqing，Mao Hongbing，Zhang Baosheng.Theoretical Research on Hollow Cylindrical Roller Bearing Without Preloading［J］.Bearing，2002（6）：1－5.

［5］劉衛群，羅繼偉，吳長春，等.滾動軸承剛度分析程序［J］.計算力學學報，2001，18（3）：375－378.Liu Weiqun，Luo Jiwei，Wu Changchun，et al.Program for the Stiffness Analysis of Rolling Bearing［J］.Chinese Journal of Computational Mechanics，2001，18（3）：375－378.

［6］李偉建，潘存云，王榮吉.空心圓柱滾子軸承剛度分析［J］.中國機械工程，2009，20（7）：795－798.Li Weijian，Pan Cunyun，Wang Rongji.Stiffness Analysis of Hollow Cylindrical Roller Bearings［J］.China Mechanical Engineering，2009，20（7）：795－798.

［7］李偉建，潘存云，王榮吉，等.空心圓柱滾子接觸變形的一種計算方法［J］.軸承，2009（8）：1－5.Li Weijian，Pan Cunyun，Wang Rongji，et al.An Analytical Method for Calculating of Hollow Cylindrical Roller Contact Deformation［J］.Bearing，2009（8）：1－5.

［8］姚齊水，楊文，余江鴻，等.彈性復合圓柱滾子軸承結構設計研究［J］.中國機械工程，2012，23（1）：2899－2902.Yao Qishui，Yang Wen，Yu Jianghong，et.Research on Structure Design of Elastic Composite Cylindrical Roller Bearing［J］.China Mechanical Engineering，2012，23（1）：2899－2902.

［9］楊文，姚齊水，余江鴻，等.彈性復合圓柱滾子軸承承載性能的理論研究［J］.機械傳動，2013，37（5）：6－9.Yang Wen，Yao Qishui，Yu Jianghong，et al.Research of Carring of Elastic Composite Cylindrical Roller Bearing［J］.Mechanical Transmission，2013，37（5）：6－9.

［10］魏延剛.空心圓柱滾子與滾道接觸應力及位移分析［J］.軸承，2003，5（5）：1－5.Wei Yangang.Study on Capacity Performance of Hollow Cylindrical Roller Bearing without Preloads［J］.Bearing，2003，5（5）：1－5.

［11］李偉健，潘存云，王榮吉.3種滾子接觸的有限元分析［J］.中國鐵道科學，2009，30（3）：109－112.Li Weijian，Pan Cunyun，Wang Rongji.Finite Element Analysis of Three Types of Roller Contact［J］.China Railway Science，2009，30（3）：109－112.