供需平衡的集裝箱船舶最大載箱量
趙夢夢,陳國慶,趙一飛,李南南
(1.上海交通大學a.船舶海洋與建筑工程學院;b.安泰經濟與管理學院,上海 200240;2.中航商用航空發動機有限責任公司,上海 201108)
0 引言
自1956年泛大西洋輪船公司開創世界集裝箱運輸的新紀元以來,集裝箱運輸以其特有的便捷、安全、廉價和高效等優越性備受廣大客戶的青睞.隨著經濟全球化的不斷深入,全球集裝箱海運量持續上升.雖然2008年的金融危機對全球貿易產生巨大沖擊,但是2004—2011年的世界集裝箱貿易量仍以年均6.89%的速度遞增(圖1).
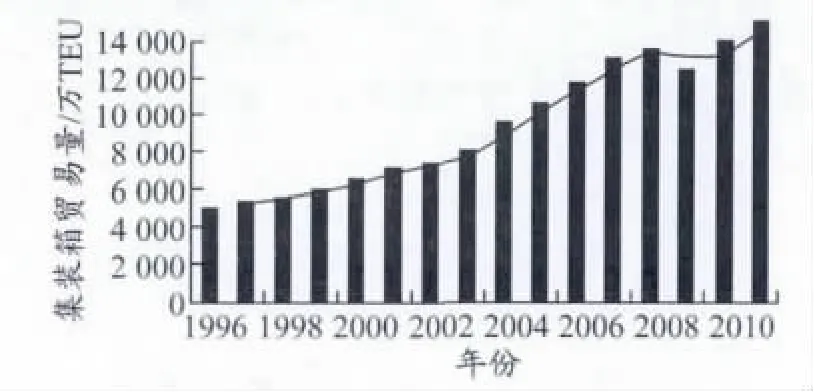
圖1 1996—2011年世界集裝箱貿易量
在全球航運市場普遍低迷的環境下,集裝箱貿易量的持續增長對班輪公司無疑是極大的激勵.為應對日益激烈的市場競爭,班輪公司積極加快集裝箱船舶大型化的步伐[1],2006年馬士基班輪公司用“艾瑪·馬士基(Emma Maersk)”號重新定義集裝箱船的最大載箱量.
目前,全球載箱量超過10000 TEU的巨型集裝箱船(Very Large Box Carrier,VLBC)總數并沒有因為全球金融風暴而停止增加的步伐,2012年底又有60多艘船舶被投入遠東歐洲航線以及太平洋航線.[2]更有甚者,2011年2月,馬士基班輪公司給出30艘18000 TEU集裝箱船的訂單.圖2為1996—2011年全球集裝箱船舶載箱能力增長情況.面對這一現實,全球班輪界必須思考:集裝箱船舶的大型化將按照怎樣的規律演變?
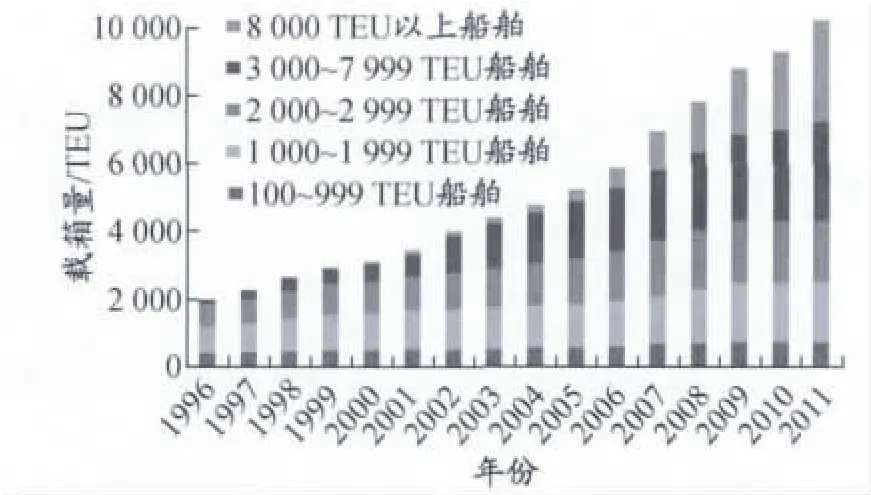
圖2 1996—2011年全球集裝箱船舶載箱能力增長情況及構成變化
趙一飛[3]從船舶規模和港口、航道等技術限制出發,對集裝箱船型規模進行預測,認為5000 TEU以上的集裝箱船舶從建造角度看技術難度可以突破,但是從航行和經濟可行性角度看存在較大的不確定性.IMAI[4]概述超大型集裝箱船的基本特征.CULLINANE等[5]分析典型航線上不同船型的單位經濟成本,以及未來船舶大型化趨勢對集裝箱營運、物流系統及碼頭的影響.CULLINANE等[6]對超大型集裝箱船的可行性作進一步研究.仇鑫堯[7]討論可行的主尺度、航速等設計參數,以利潤為目標,以費用-效益分析方法對中遠發展7000 TEU集裝箱船進行技術可行性分析和論證.吳沖[8]對集裝箱船舶大型化的規模經濟效益優勢進行分析,建立集裝箱船舶運輸成本模型,對不同規模集裝箱船舶的成本差異進行相對評價.張仁頤[9]給出在航線上貨運量已知條件下集裝箱船舶最大載箱量的計算方法.BRANCH等[10]從全球適箱貨貿易增長的周期性出發,表示出對VLBC發展速度的擔憂.以上對集裝箱船大型化的研究基本立足于船舶經濟性和技術可行性等方面,他們的預言多數都被業界的實際發展狀況所突破.
1 集裝箱船大型化和巨型船舶的概念
集裝箱船舶大型化趨勢有兩個含義:一個是集裝箱船舶平均箱位的增長;另一個則是船舶最大載箱量的提高.20世紀60年代,集裝箱船的平均箱位運力不足300 TEU;到20世紀70年代末,這一數字迅速上升到620 TEU;據德國航運經濟與物流研究所統計,20世紀80年代末達到 1200 TEU;據CLARKSONS統計,1995年末世界集裝箱船單船平均運力1500 TEU,到20世紀末該數字進一步增加到1756 TEU;截至2012年9月1日,世界集裝箱現役船隊的平均運力已達到3134 TEU,船舶大型化已是集裝箱船隊發展的主流.[11]
關于集裝箱船的最大載箱量,航運界與造船界的認識不同.1982年底,在荷蘭鹿特丹舉行的討論會上,西班牙的造船專家們提出一種預計可裝運3400只40英尺集裝箱(或6800只20英尺集裝箱)的集裝箱船設計方案,在當時被稱為巨型集裝箱船.隨著造船技術的不斷發展,2005年集裝箱船的最大載箱能力增長到8000 TEU.到2011年,載箱量18000 TEU的船已經開始建造,根據建造進度,這些船舶應該在2013年投入運營.
導致上述變化的原因無疑是全球貿易的增長.但是有關全球貿易與船舶大型化趨勢關系的研究,大多建立在定性分析以及數量的相關性分析基礎上,尚未有人給出明確的算法和結論.本文試圖基于供需平衡理論探討全球集裝箱貿易量與集裝箱船最大載箱量之間的關系,以幫助班輪公司確定最大載箱量的船舶投入市場的時間,對于班輪公司的投資決策具有重要意義.
2 建模
假設全球集裝箱貿易量穩定增長,各大班輪公司的新造船投資都是理性的,即每家班輪公司的造船計劃均是根據航線增長計劃制訂的,而航線增長計劃又是由航線兩端港口之間的貿易增量決定的,針對基于集裝箱船舶運力供給與全球集裝箱貿易量供求平衡的情況可以進行如下分析.
設t年度集裝箱船舶的最大載箱量為Yt,該年全球集裝箱貿易量為Tt,兩個變量之間的關系可表示為

式(1)中,Tt是自變量,它主要隨全球GDP的增長率、主要經濟體的貨幣發行量、利率以及主要貨幣之間匯率的變動而變動,但Yt的大小對其只是約束作用.反過來,Yt與 Tt正相關,Tt越大,Yt就越大;但是Tt一旦變小,Yt卻保持在Tt最大值時的數值上,一般不會同步下降.
為找出Yt與Tt的函數關系,首先要取得分析期各年份的Yt和Tt,見表1.
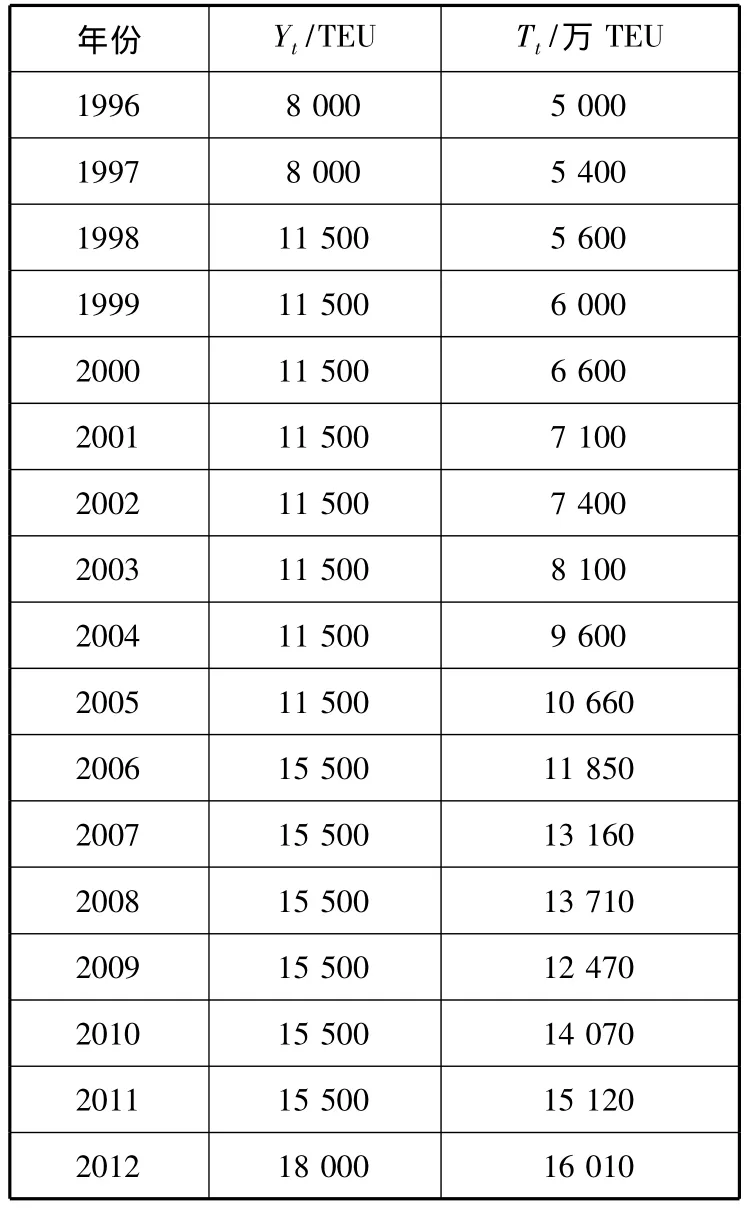
表1 分析期各年份的集裝箱船最大載箱量和相應的集裝箱貿易量
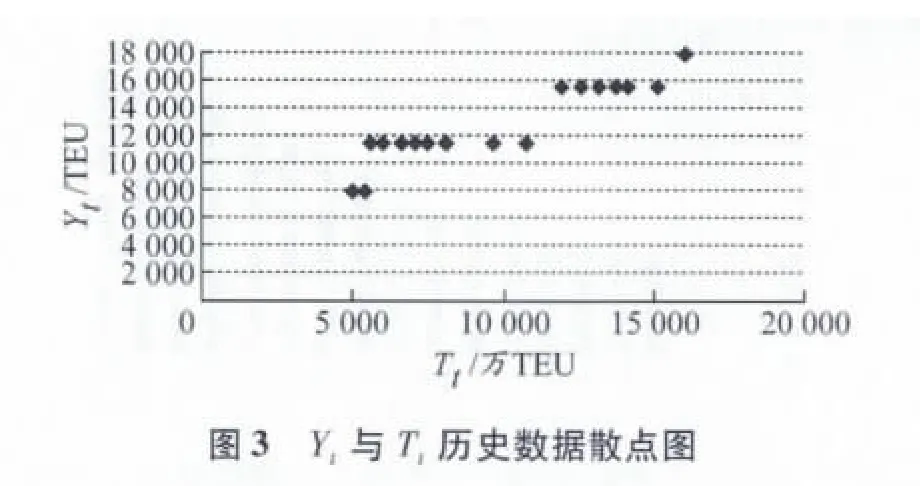
求解此類問題通常都會采用回歸方法尋找二者之間的函數關系.[12]但是從運用表1的數據所作的散點圖(圖3)可見,Yt與Tt之間不存在顯著的函數關系.顯然,回歸方法不適合解決此類問題,必須另辟蹊徑.
根據國際海事組織(International Maritime Organization,IMO)公布的1996—2012年間各年度集裝箱船隊的數據,可以作出如圖4所示的曲線族,其中縱軸為船舶的載箱量yt,橫軸是對應一定載箱量的船舶數量nt.
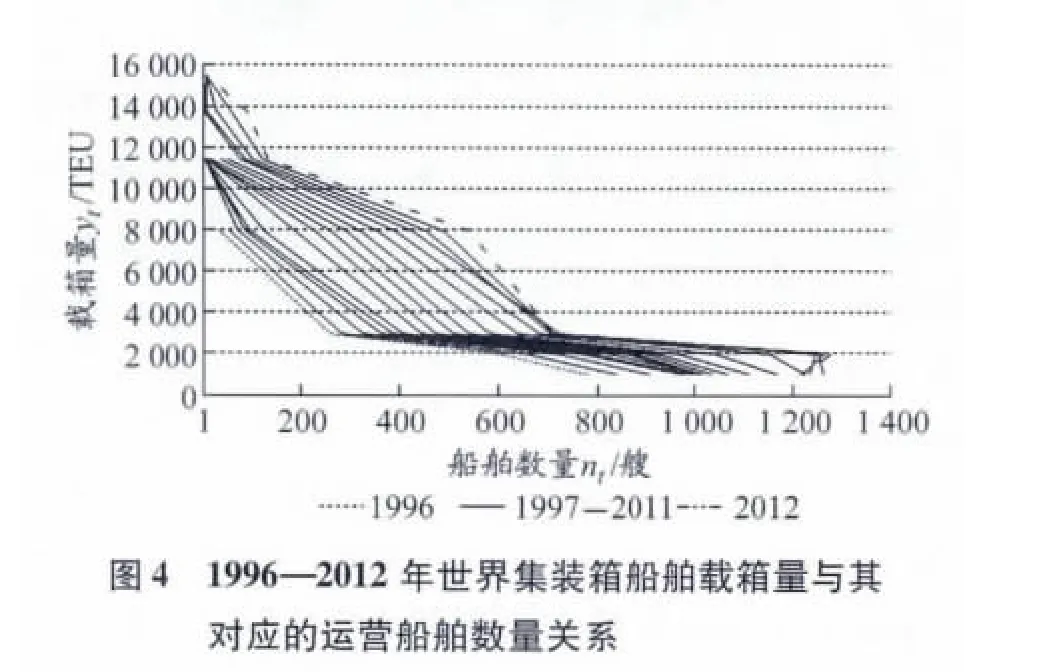
由圖4可見,集裝箱船舶的載箱量與其數量存在負相關性,也就是載箱量越大的船舶,其數量越少.因此,可以寫出函數關系式

式中:yt為t期船舶的載箱量;nt是t期對應一定載箱量的船舶數量,且<0.
每年的全球集裝箱貿易量均由集裝箱船舶完成,因此有
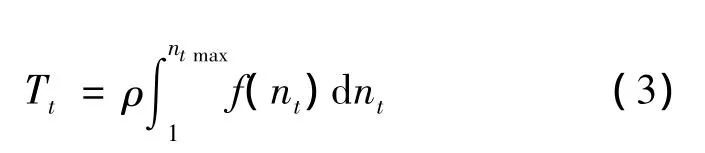
式中:ntmax為t期最小船型的數量;ρ為運力運量轉換系數.
3 驗證
顯然,要求解式(3)存在一定困難,因此需要尋找簡化的方法.
3.1 模型簡化
由于船舶大型化不僅考慮單船載箱量,還與特定船型的投入數量有關.考察圖4,式(2)所對應的曲線族的斜率在yt≈3000 TEU時出現較大改變,這使式(2)的函數關系不易被很快發現.但是,從當前全球航線運營的船舶載箱量分布看,能夠成為最大型船舶替代者的只可能是載箱量在3600 TEU以上的船舶.考慮到本文的研究內容,可以不考慮載箱量為3000 TEU以下船舶的情況.而圖4中,當載箱量為3000 TEU以上時,各年度的對應載箱量與船舶數量之間的關系幾乎為一直線,因此可以假定yt與nt的關系為線性函數,即存在
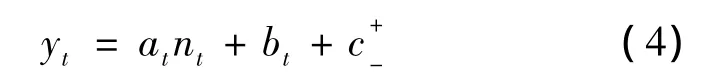
式中:at為計算年度曲線的斜率(at<0);bt為計算年度船舶載箱量的截距;c+-為預測集裝箱船舶最大載箱量與當年實際最大載箱量之差,取絕對值.模型分析流程見圖5.
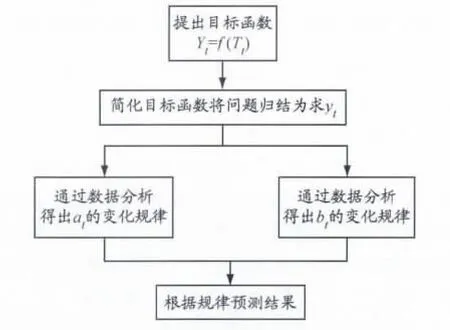
圖5 模型分析流程
將圖4中的數據按年度分別代入式(4)進行線性回歸計算,結果見表2.
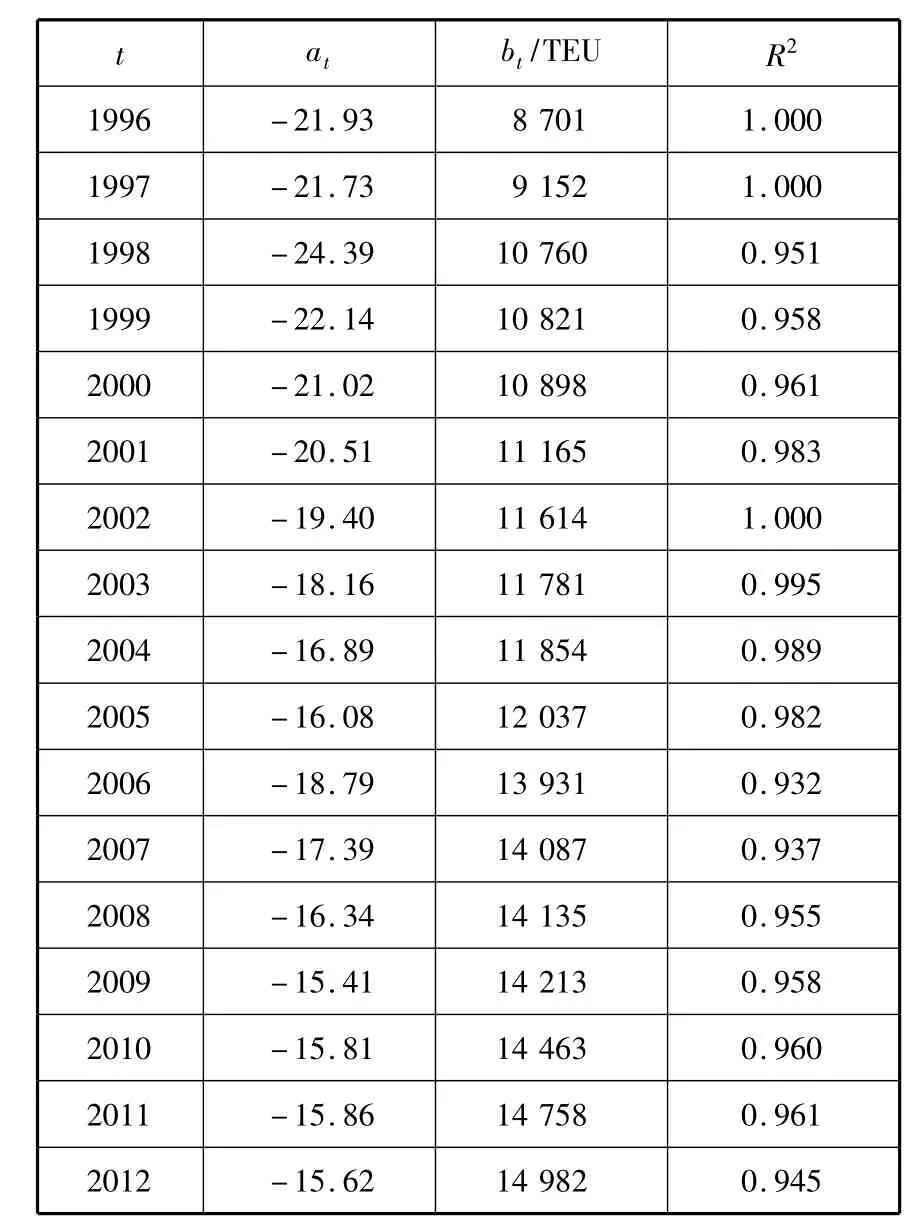
表2 圖4中各曲線線性回歸數據
由表2可知:計算期內各年的船型和數量方程與實際數據的擬合度均滿足合理性要求,R2最小的也為0.932;但是at和bt均不為常數,具體而言就是這些曲線相互間不平行,且間距也不固定,但都可以獲得船舶載箱量與船舶數量曲線,見圖6.
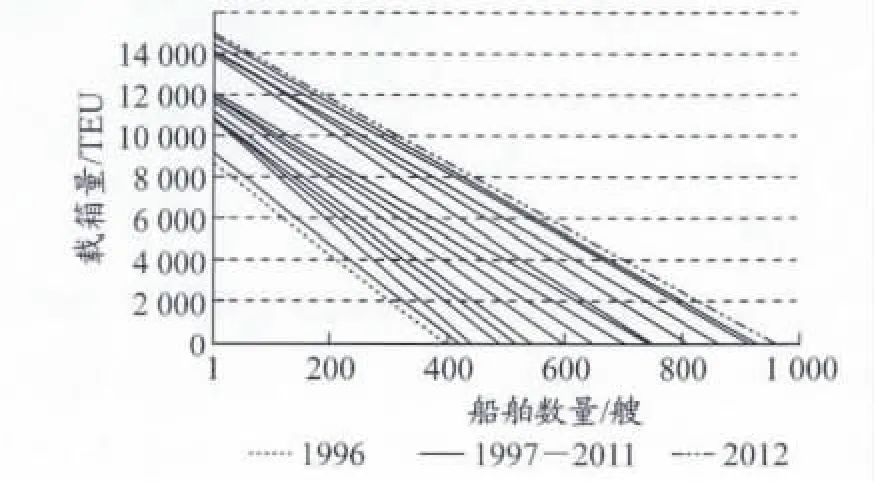
圖6 1996—2012年船舶載箱量與船舶數量線性趨勢線分布
3.2 試算
這里嘗試用時間序列求出at和bt的變化規律.
3.2.1 計算 at
先作出at的時間序列散點圖,見圖7.通過線性回歸,可以得出at的計算式
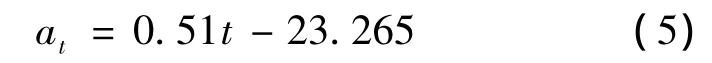
式(5)的R2=0.8329>0.75,可以認為其符合線性規律.
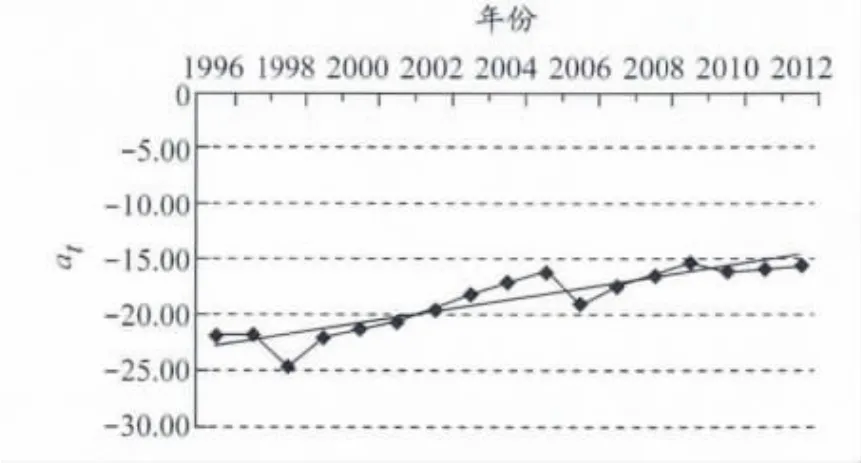
圖7 1996—2012年趨勢線斜率
3.2.2 計算 bt
先作出bt的時間序列散點圖,見圖8.通過線性回歸,可以得出bt的計算公式
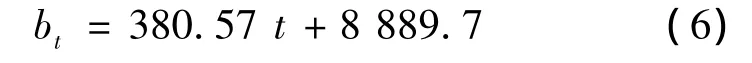
式(6)的 R2=0.9459>0.75,可以認為其符合線性規律.
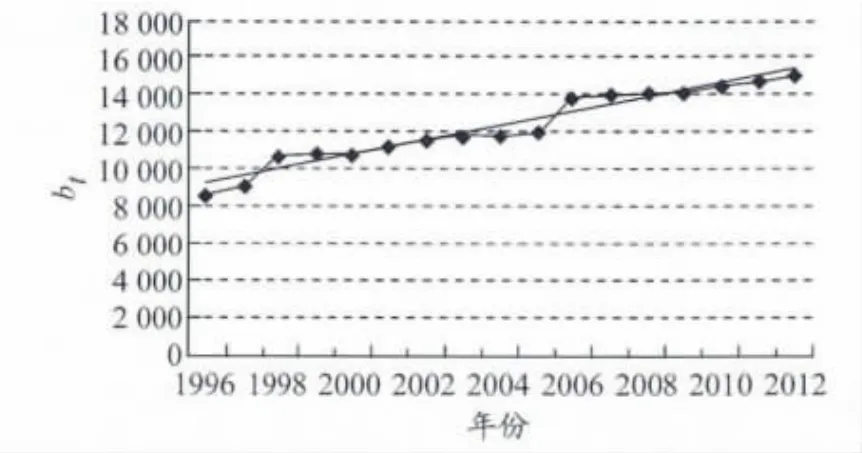
圖8 1996—2012年趨勢線截距
3.3 誤差求取
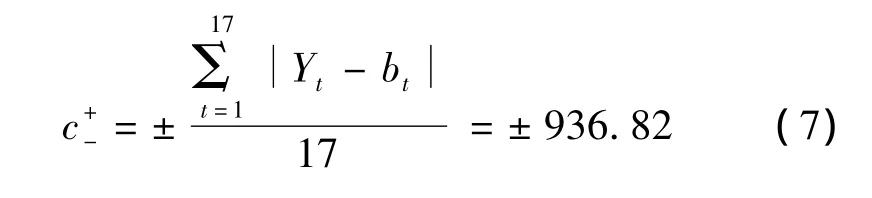
3.4 預測
根據式(5)和(6),可以分別求出預測年份的at和bt,代入式(4)即構成預測年份的載箱量與船舶數量關系函數.在本例中,可以預測出2020,2025和2030年載箱量與船舶數量關系函數,分別見式(8),(9)和(10).
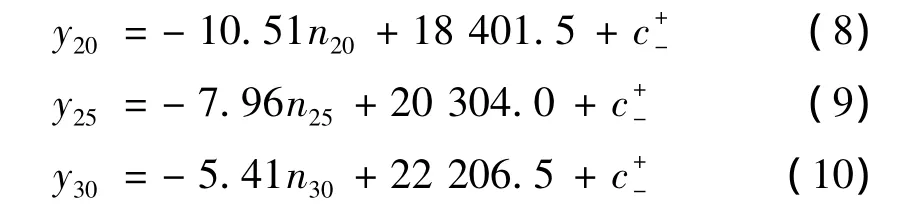
從2020年到2030年各主要預測年份的載箱量與船舶數量關系曲線見圖9.在式(10)中,當n30取值為最小值1時,y30取值為

4 結束語
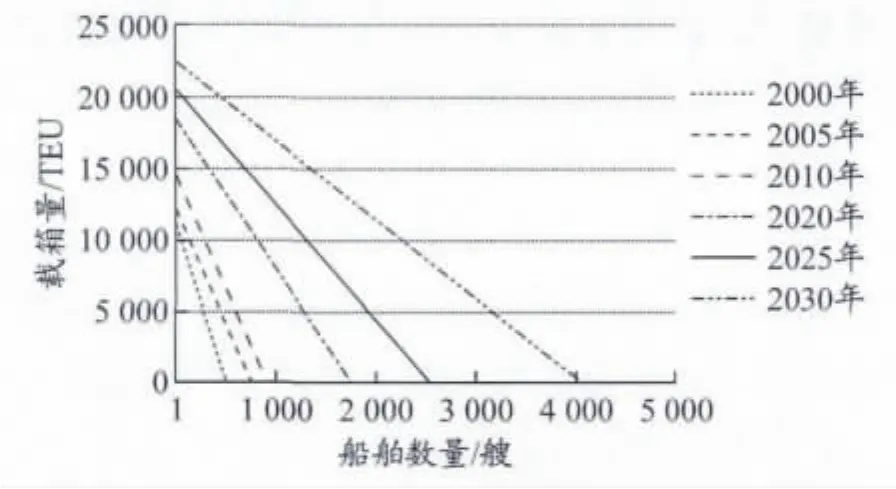
圖9 2020,2025和2030年集裝箱船型發展趨勢預測
采用圖形分析與時間序列回歸相結合的方法,給出集裝箱船舶最大載箱量的算法.根據這一算法,可以較為準確地估計出未來年份將出現的最大集裝箱船舶載箱量.這對船舶設計部門、建造部門以及港口企業無疑是十分重要的.本文沒有考慮航道、碼頭等對船舶大型化的限制,主要是因為此類大型船舶多數安排在大洋航線上.當然,影響集裝箱船舶大型化的因素很多,如港口設施[13-14]、國際經濟走向、經濟一體化[15]、船舶技術和世界航運格局等.
本算法僅僅是在集裝箱船型領域的一項探索,其計算精度也需要采用更為合理的算法加以提高.希望這種思路也可以用于干散貨、油船等其他類型船舶的最大載貨量預測上.
[1]鄭樓先,林曉東.集裝箱船舶大型化的利與弊[J].船海工程,2005(4):79-80.
[2]陳飛兒,張仁頤.基于水運系統的超大型集裝箱船經濟可行性論證[J].船舶工程,2008,30(1):78-81.
[3]趙一飛.論集裝箱船的大型化趨勢[J].上海造船,1995(3):1-7.
[4]IMAI A,NISHIMURA E,PAPADIMITRIOU S,et al.The economic viability of container mega-ships[J].Logistics & Transportation Rev,1997,21(4):32-34.
[5]CULLINANE K,KHANNA M.Economies of scale in large container ships[J].J Transport Econ & Policy,2000,33(2):185-207.
[6]CULLINANE K,KHANNA M.Economies of scale in large containerships:optimal size and geographical implications[J].J Transport Geography,2000,8(3):181-195.
[7]仇鑫堯.中遠集團建造超大型集裝箱船技術經濟可行性分析[D].上海:上海海運學院,2003:37-41.
[8]吳沖.集裝箱船舶大型化規模經濟研究[D].上海:上海海事大學,2005.
[9]張仁頤.水運物流系統分析[M].上海:上海交通大學出版社,2007:87-88.
[10]BRANCH A,STOPFORD M.Maritime economics[M].3rd ed.Oxon:Routledge,2009:45-47.
[11]CLARKSONS.Container intelligence quarterly[R].Third quarter 2012:13.
[12]陳麗江,蘇含秋.中國國際集裝箱班輪運輸市場運價趨勢分析[J].上海海事大學學報,2005,26(4):75-76.
[13]高潔.上海港集裝箱運輸競爭力評價[J].上海海事大學學報,2005,26(4):67-72.
[14]曹金虎,薛士龍,陳加敏,等.基于PLC和組態王的高效自動化集裝箱碼頭監控系統設計[J].上海海事大學學報,2011,32(2):25-28.
[15]郭永紅.集裝箱船大型化經濟性分析[D].大連:大連海事大學,2000.

