同倫法部分極點配置中特征靈敏度計算

吳晶瑩，王冠楠

（浙江大學 電氣工程學院，浙江 杭州 310027）

0 引 言

隨著電力事業的蓬勃發展，電力系統規模不斷擴大，電力網絡日益復雜，電網運行越來越容易接近穩定極限。使得低頻振蕩現象屢屢發生，嚴重時會引起停電事故，給經濟造成了巨大的損失也給社會安定帶來了不良的影響［1-2］。因此，分析電力系統低頻振蕩及其抑制措施具有非常重要的現實意義。阻尼是影響低頻振蕩的關鍵，安裝電力系統穩定器（Power System Stabilizer，PSS）作為一種經濟有效的阻尼抑制方法得到了廣泛的應用。而如何合理配置、選定電力系統穩定器參數是備受關注的問題［3-4］。

極點配置作為PSS參數配置的常用方法已經被廣泛使用，文獻［5］采用全部特征值，雖然魯棒性好，但對于大系統常常會出現所謂“維數災”的問題。文獻［6-8］分別利用選擇模式分析法、AESOPS法、S矩陣法，以確保計算精度和速度都可以滿足大電力系統的要求，但計算結果受到搜索初值和范圍的影響很大，不能保證所有的負阻尼和弱阻尼模式都被搜索到。另外牛頓法［9］，初值的依賴性非常強，而對初值求解往往很復雜。文獻［10］驗證了最小二乘同倫法的可行性，以及它的收斂速度和魯棒性都比經典的牛頓法好很多。

目前在電力系統研究領域中對于特征靈敏度研究雖有不少，卻多為針對特征值靈敏度的分析，對于特征向量及其在電力系統的計算分析卻很少見，傳統的特征向量靈敏度的計算方法如文獻［11］中所述需要知道所有的特征向量才能求取特征向量靈敏度并且僅適用于只有一些特征向量的小系統，不適用于大系統。文獻［12］提出了特征靈敏度分析方法，但是又由于負荷矩陣的稀疏性或者數值不穩定，對實際系統的分析并不可行。

本研究提出一種基于最小方差全概率同倫法的極點配置方法，以PSS可調參數為優化變量，以部分極點配置為目標，通過利用多種特征向量靈敏度分析方法實現小干擾下PSS的參數優化配置，并且著重分析特征靈敏度在其中的計算，分析多種特征值靈敏度、特征向量靈敏度的計算方法，利用經典的3機9節點系統和New England10機39節點系統算例分析該方法的可行性。

1 小信號穩定及簡單的PSS模型

根據數學模型的不同類型［13］，電力系統小干擾穩定性分析的方法可以分為4類:數值仿真法、特征值分析法、頻域分析法和非線性理論分析法［14］。而特征值分析法是一種成熟的小干擾穩定研究方法，也是公認非常有效的分析方法，它以線性系統和李雅譜諾夫第一定律為基礎，將系統在平衡點線性化，形成狀態方程矩陣，計算特征值、特征向量、參與因子等信息。

PSS是抑制低頻振蕩最簡單有效的方法，本研究中PSS調試的是單機無窮大系統。通過配置多個標準的二階電力系統穩定器模型實現，示意圖如圖1所示。

圖1 標準的二階電力系統穩定器

其傳遞函數為:

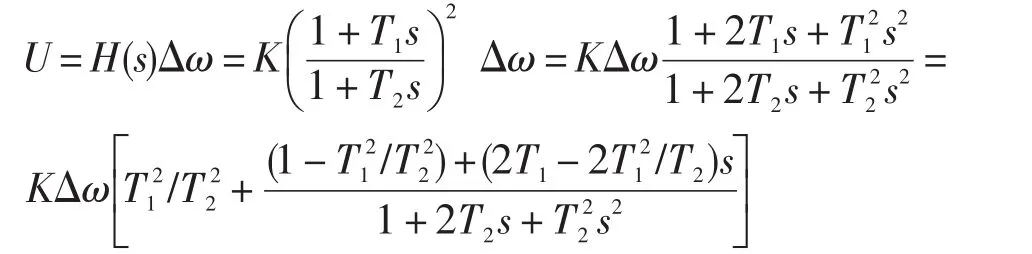
設PSS的狀態變量為:

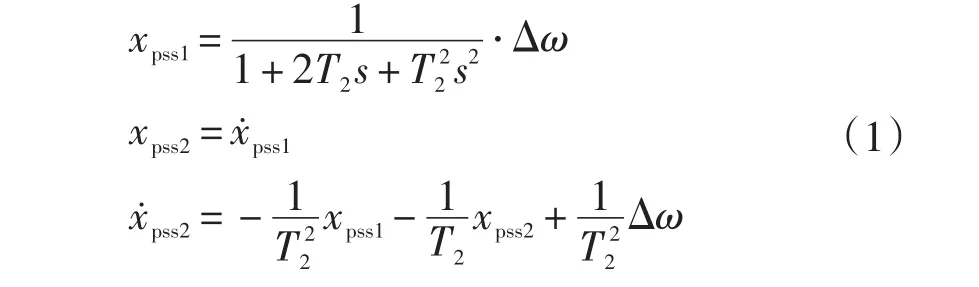
綜合以上結果，制定一個PSS狀態方程，輸入Δω為:

閉環系統的狀態矩陣及其系數的偏導為:

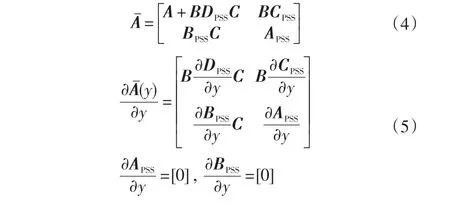
2 最小方差同倫法極點配置

研究者設計PSS參數的時候，對于控制反饋環節，將系統中不符合穩定運行條件的極點重新配置到復平面內合理的位置，使得新的系統符合動態穩定標準，振蕩得以被抑制。

又因為知道閉環系統可以表示為式（4），在傳統方法中，極點配置問題可以認為是求解目標函數方程:

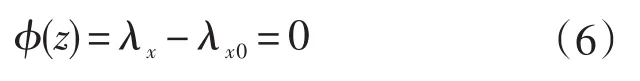
然而，目標函數方程并不一定有解，為了增加極點配置問題的可解性，引入最小方差極點配置，它具有如下的特點:無需使用泰勒法展開非線性模型，理論嚴密，特別適合求解非線性強度較高的模型；對初值依賴性極低，具有大范圍收斂性，數值解穩定，且精度高。它的目的是讓目標解與目標值的距離的平方和最小［15］:

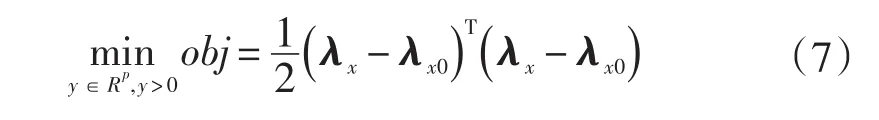
相當于上式滿足:

下面引入同倫法的概念，它作為代數拓撲學（To?pology）的基本概念，來源于延拓法，通過對不穩定的最優化問題添加一個穩定泛函，把它變為一個穩定的最優化問題［16］。自19世紀初開始作為數值工具用于求解一般的非線性方程組，至今已取得了卓越的成果。具體的求解過程如下，設有一個非線性方程組:

設z1,z2為p維空間Rp的非空子集，?:z1→z2為一個光滑的同倫映射。在同倫算法中，并不是直接求解式（9），而是在其中加入一個已知其解或者易于求解的方程φ(z)，配合同倫參數，構造同倫方程:

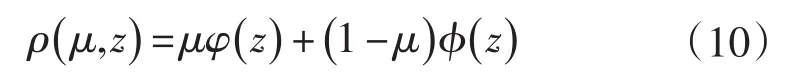
其中，μ∈[0,1]，ρ(μ,z)為同倫函數，且本研究采用的是全概率同倫法，即概率為1，‖μ˙,z˙‖2=1，即同倫方程具有以下關系:

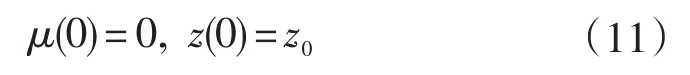
利用參考文獻［17］中所用的方法，求解如下:

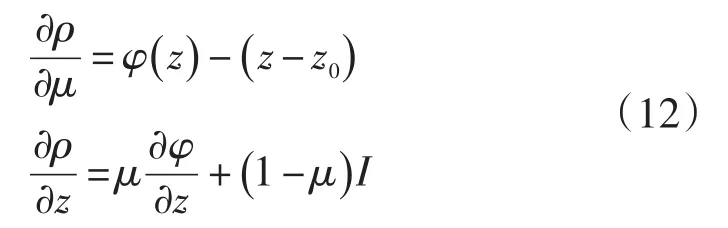
為了利用同倫算法還需要知道φ(z)的雅可比矩陣如下所示（其求解過程將在下文中詳細敘述）:

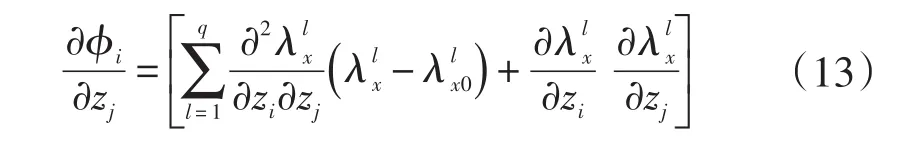
3 特征靈敏度的分析

由公式可以知道，需要求解同倫算法需要知道特征值一階靈敏度、特征值二階靈敏度、特征向量靈敏度，具體的求解過程將在下文詳述。

3.1 特征值一階靈敏度

對于系統的狀態矩陣A有以下方程:

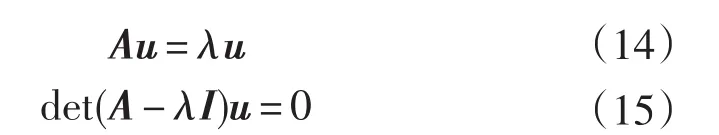
式中:λ—A的特征值，λ=[λ1,λ2,...,λn]；u—右特征向量；v—左特征向量。

用viTui=Ci=1進行標準化，來求解特征值一階靈敏度?λ/?zi，將式（14）關于zi求導，可得:

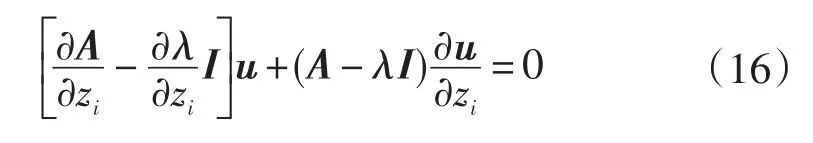
再對上式兩邊都左乘vi，整理可得:

3.2 特征值二階靈敏度

除了需要求解特征值的一階靈敏度，還需要求解特征值的二階靈敏度。將上式關于zj求導，可得:

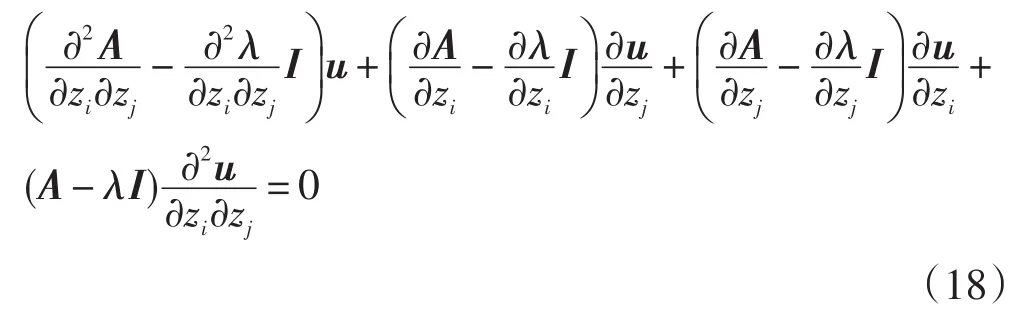
將上式的左右兩邊都乘以vT，化簡可得:

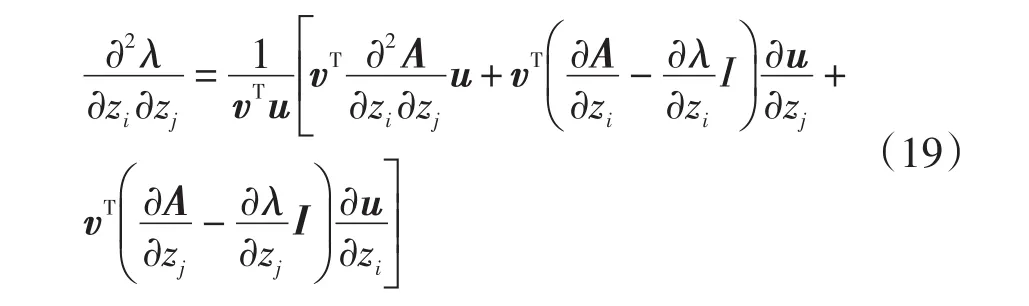
為了求解二階特征值靈敏度需要知道:第i個特征值的左右特征向量v,u；第i個特征值關于參數zi,zj的一階特征值靈敏度；狀態矩陣的二階偏導數；特征向量關于參數zi,zj的一階特征值靈敏度。

這表示要求解特征值的一階、二階靈敏度，并不需要求解狀態矩陣的所有特征值。

3.3 特征向量靈敏度

特征靈敏度的計算主要是指特征值和特征向量導數的數值計算。特征值導數的計算比較容易，困難在于特征向量導數的計算。由上可知，為了求解特征值二階靈敏度，其中最關鍵的就是會求解右特征向量一階靈敏度。常見的計算方法主要可以分為以下5種［18］:①差分法；②模態法；③NELSON類方法；④代數法；⑤迭代法。

其中，差分法和迭代法又屬于數值法，而NELSON法、模態法屬于解析法。由于大部分特征靈敏度的研究是集中在機械、土木、航空、航天等方面，研究的系統大多數為對稱無阻尼系統，而小干擾穩定運行的環境是實非對稱系統，所以其中的大量方法并不可行，下面本研究選擇了切實可行且具有代表性的幾種算法對特征向量靈敏進行求取:

3.3.1 FOX和KAPOOR的方法

1968年FOX和KAPOOR［19］首先提出了特征值導數和特征向量的求解方法，利用完整的模態展開法，對對稱無阻尼系統給出了特征值和特征向量一階導數的精確求解。該方法指出:將式（14）的兩邊進行求導，可得:

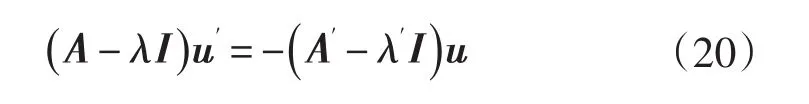
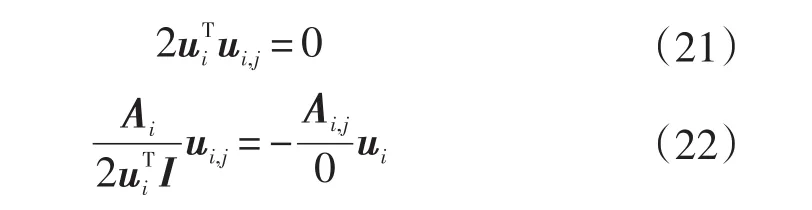
當方程具有n個互不相同的特征值時，(A-λI)為奇異陣，秩為n-1，此時特征向量靈敏度可以由下式所求:

由此可見，利用經典的模態展開法來進行特征向量靈敏度的求解，需要知道所有的特征值、特征向量，對于維數大的向量系統而言是一個異常復雜的過程。

3.3.2 John Condren的方法

在文獻［20］中，John Condren提出了一種求解特征向量靈敏度的方法，因為:

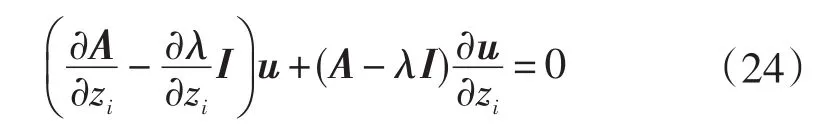
其中:A-λI是奇異的，所以無法在式子兩邊直接左乘(A-λI)-1來求解特征向量靈敏度。因此本研究提出了一種標準化條件:

所以研究者可以構造方程，利用標準化方程來分別求解特征向量一階靈敏度的實部和虛部:

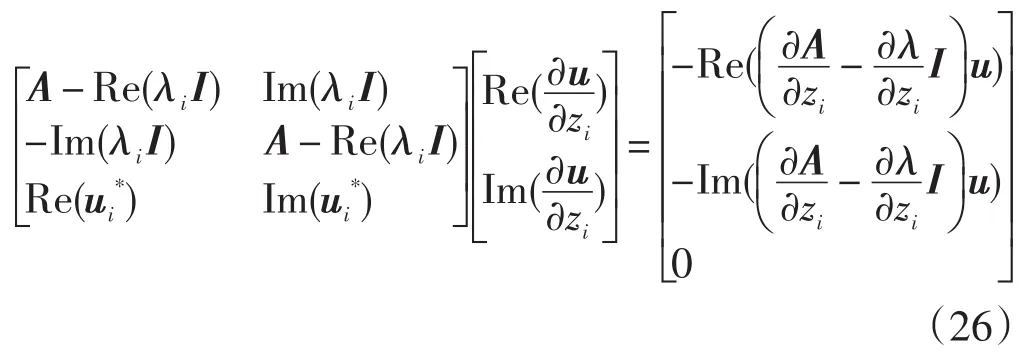
使用該方法時，只要知道需要配置的特征值以及它所對應左、右特征向量即可。

3.3.3 M.jankovic的方法

另一種方法利用文獻［21］中所提的新的約束條件，首先將下式:

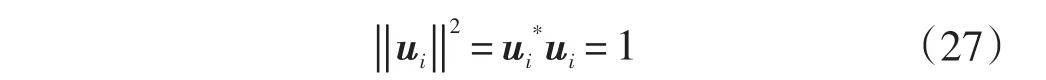
關于zi求偏導，可以得到:

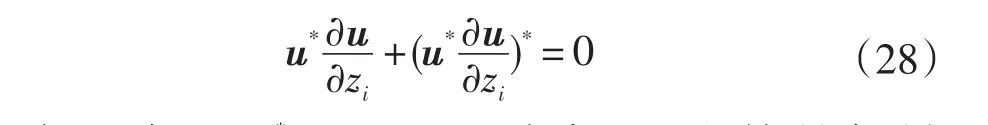
方程在 Im[u*(?u/?zi)]=0 時成立，也就是如果u*(?u/?zi)是實數，那么上式u*(?u/?zi)+[u*(?u/?zi)]*=0 成立，可以變為:

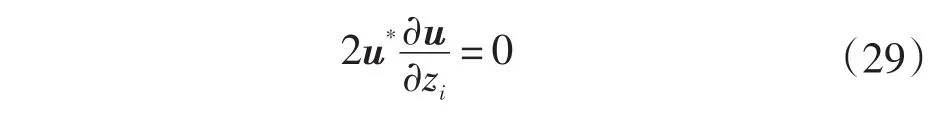
若u*?u/?zi=0 兩邊左乘u，可以得到:

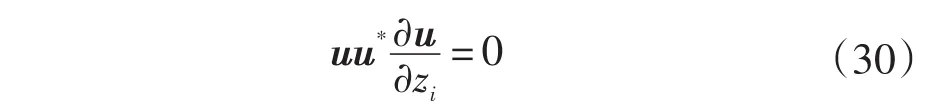
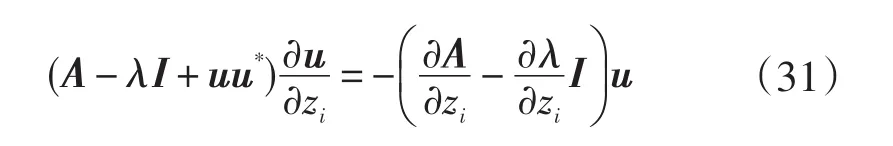
同樣也可以利用上式展開分別求解特征向量的實部和虛部獲得所求解。3.3.2節中的方法和3.3.3節中的方法主要區別是利用不同的歸一化條件進行運算分析。

3.3.4 NELSON的方法

以NELSON［22］為代表的一系列方法都稱為直接法，它就是直接處理特征值向量導數在控制方程中系統矩陣的奇異性。其基本思想是把特征向量導數表示為齊次方程的通解和非齊次方程的特解的和的形式，再對兩部分分別求解，假設:

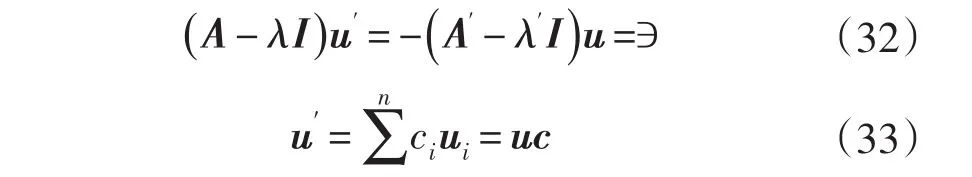
聯立可得:

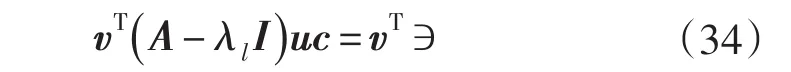
又因為vTAu=diag(λ)，那么方程等于:

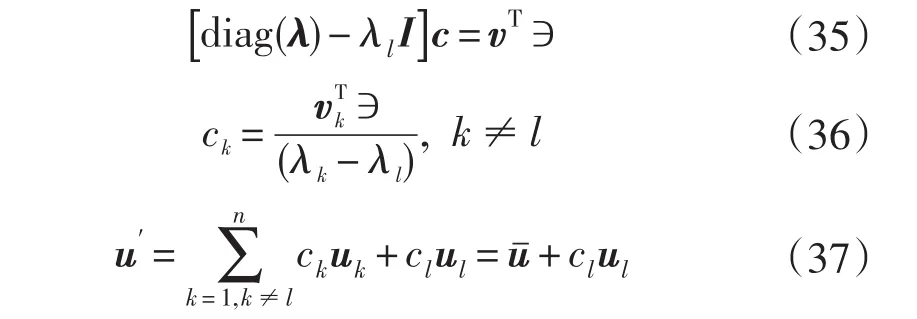
uT*u=1，取偏導，得:

將式（37）代入，可以求得:

求解u′的關鍵是求解uˉ，考慮齊次方程:

也可以表示成:

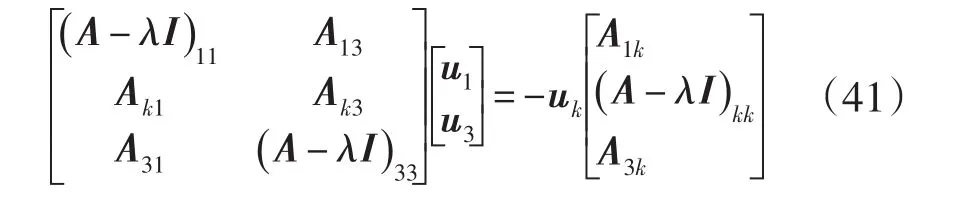
如果uk≠0，那么 (A-λI)的第k列，是剩下（n-1）列的線性組合。同理可得，對于左特征向量v:

如果vk≠0，那么(AT-λI)的第k列是(A-λI)剩下的（n-1）行的線性組合。綜上所述，可得如果vk≠0，uk≠0，那么(A-λI)的第k行第k列都可以刪除，則u1,u3滿足:

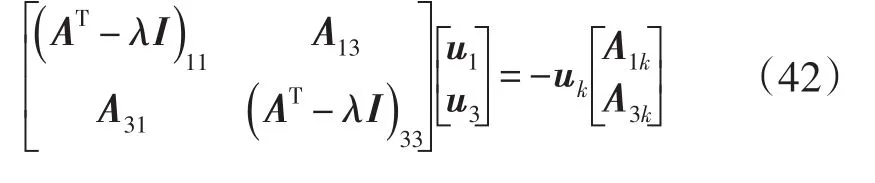
綜上所述，第i個特征值所對應的特征值向量靈敏度可以表示為:

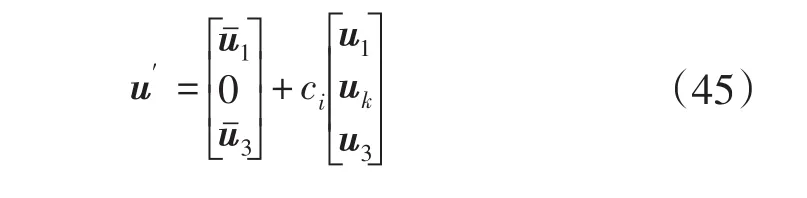
這樣就得到了u′，然后利用LU分解法來求解PSS超前滯后環節的參數。

NELSON計算的優點是不用求解每一個特征值，只要求解需要的特征值即可，保持了結構特征值問題的對稱性和帶寬特點，但在求解重根特征值時有局限性。

4 算法實現

算法實現過程如下:

（1）初始化系統參數；

（2）求取系統的閉環狀態矩陣A；

（3）求取特征值以及相應的左、右特征向量λ,v,u；

（4）求取特征向量靈敏度?u/?zi；

（5）利用最小方差同倫法求?ρ/?zi；

（6）利用改進歐拉法求得μ,zi；

（7）得到配置后的極點以及PSS參數；

（8）判斷結果是否提高了阻尼、降低了振蕩頻率。

運算流程圖如圖2所示。

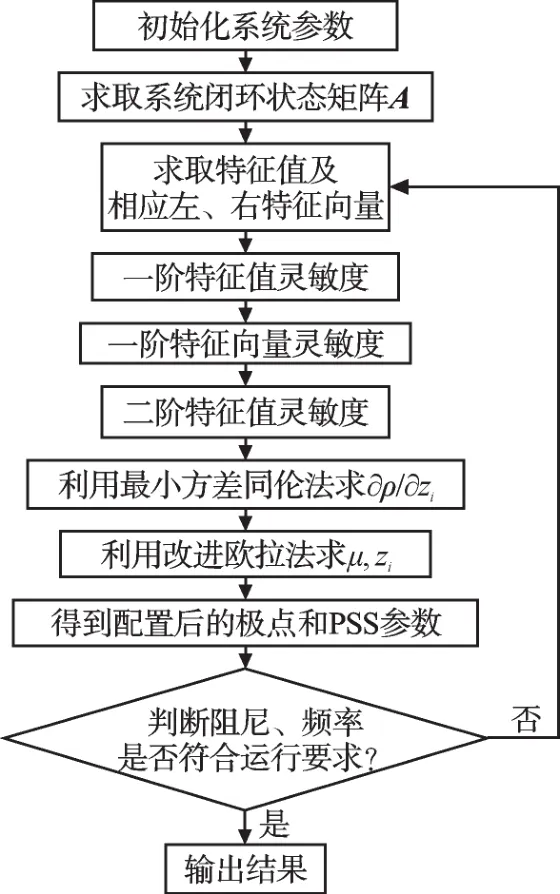
圖2 運算流程圖

5 算 例

5.1 3機9節點算例

為了進一步驗證上述同倫求解極點配置的方法是有效的，本研究引入的3機9節點系統如圖3所示，該系統是一個經典的小信號穩定分析系統，它有3臺發電機、3個負荷、9條輸電線路。

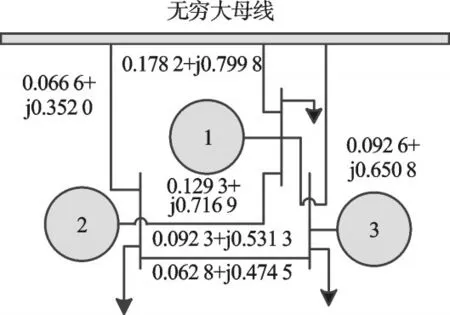
圖3 系統接線圖

3.3.1 節中的方法在運算速度上已經非常緩慢，下面本研究使用3.3.2節、3.3.3節、3.3.4節中的方法分別進行極點配置，將系統的特征值配置到目標極點的位置，初始Ta=［0.16，0.19，0.165］；K=［44.5，83.5，25.50］，如圖4所示。

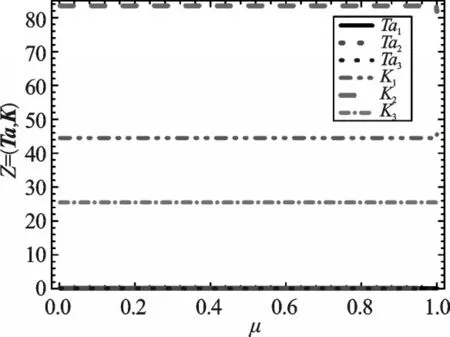
圖4 Ta和K隨著μ變化到1的變化

隨著特征值λ1-λ6達到想要配置的點，參數Ta、K的變化過程如圖5所示，最終在μ=1的時候停止，是一個全概率的過程。以及在這個過程中，特征值λ1-λ6也都被配置到了目標位置。此時參數Ta=[0.164,0.194,0.169]，K=[44.119,83.956,25.504]，λ=[-3.997,-3.617,-1.899,-8.364,-10.984,-13.689]。

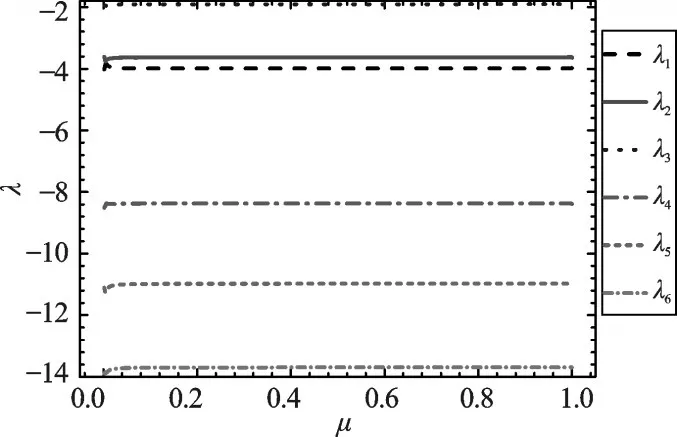
圖5 λ1-λ6隨著 μ變化到1的變化

5.2 New England 10機39節點算例

同時針對New England 10機39節點的系統算例，本研究分別使用上述幾種方法對其進行計算，初始Ta和K為:Ta=[0.250 65,0.250 88,0.269 38]，K=[25,25,25.000 16]，采用3.2.2節方法時卻發現由于rank=n-1，3.3.2節方法產生的最優解具有數值錯誤，而3.3.3節、3.3.4節方法仍然適用，配置結果如圖6、圖7所示。

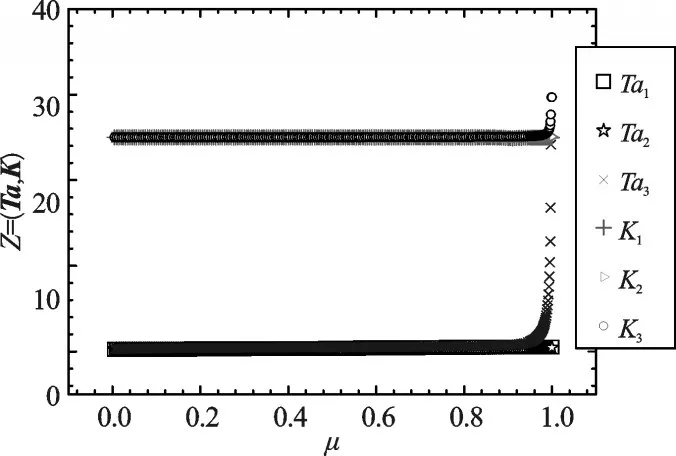
圖6 Ta和K隨著 μ變化到1的變化

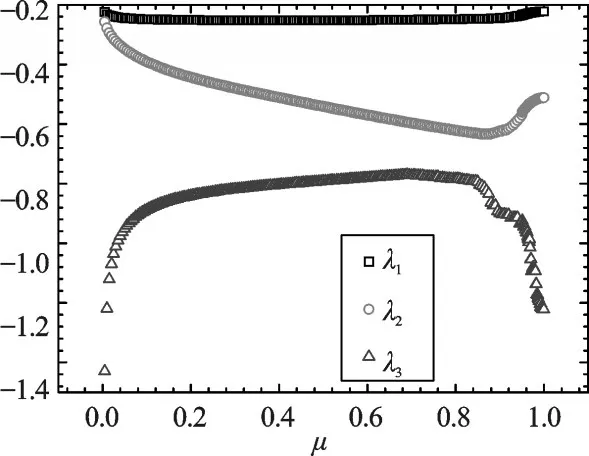
圖7 λ1-λ3隨著 μ變化到1的變化

可以看到通過3.3.2節、3.3.3節、3.3.4節方法，都能夠將特征值配置到目標位置，但是相比3.3.4節方法，3.3.2節、3.3.3節方法雖然計算過程簡單，但是在求解大系統的時候會出現不穩定，求解矩陣奇異，稀疏性較差，無法求得精確解。3.3.4節方法具有更好的魯棒性。

6 結束語

本研究介紹了特征靈敏度在同倫最小方差極點配置中的計算，其中對于特征向量靈敏度分別提出了3種計算方法，通過對算例的比較分析驗證了3.3.2節方法和3.3.3節方法的可行性，但它們稀疏性較差且大系統時矩陣會出現病態，3.3.4節方法具有更好的適用性、魯棒性以及特征靈敏度計算方法的可行性和有效性。

（References）:

［1］朱 方，趙紅光，劉增煌，等.大區電網互聯對電力系統動態穩定性的影響［J］.中國電機工程學報，2007，27（1）:1-7.

［2］余貽鑫，李 鵬.大區電網弱互聯對互聯系統阻尼和動態穩定性的影響［J］.中國電機工程學報，2005，25（11）:6-11.

［3］王 康，金宇清，甘德強，等.電力系統小信號穩定分析與控制綜述［J］.電力自動化設備，2009，29（5）:10-19.

［4］韓禎祥，薛禹勝，張伯明.1996年國際大電網會議（CI?GRE）第37，38，39組簡介［J］.電力系統自動化，1997，21（1）:45-48.

［5］袁 野，程 林，孫元章.采用廣域測量信號的 2級 PSS控制策略［J］.電力系統自動化，2007，30（24）:11-16.

［6］ROUCO L，PEREZ-ARRIAGA I J.Multi-area analysis of small signal stability in large electric power systems by SMA［J］.Power Systems，IEEE Transactions on，1993，8（3）:1257-1265.

［7］SAUER P W，RAJAGOPALAN C，PAI M A.An explana?tion and generalization of the AESOPS and PEALS algo?rithms［power system models］［J］.Power Systems，IEEE Transactions on，1991，6（1）:293-299.

［8］UCHIDA N，NAGAO T.A new eigen-analysis method of steady-state stability studies for large power systems:＜ e1＞S＜/e1＞ matrix method［J］.Power Systems，IEEE Transac?tions on，1988，3（2）:706-714.

［9］ANGELIDIS G，SEMLYEN A.Improved methodologies for the calculation of critical eigenvalues in small signal stabili?ty analysis.Power Systems［J］.Power Systems，IEEE Transactions on，1996，11（3）:1209-1217.

［10］WANG Guan-nan.A Probability-one Homotopy Method for Partial Pole Assignmen［tC］.CEPSI 2012.Bali，2012.

［11］WANG K W，CHUNG C Y，TSE C，et al.Multimachine ei?genvalue sensitivities of power system parameters［J］.Pow?er Systems，IEEE Transactions on，2000，15（2）:741-747.

［12］NAM H K，KIM Y K，SHIM K S，et al.A new eigen-sensi?tivity theory of augmented matrix and its applications to power system stability analysis［J］.Power Systems，IEEE Transactions on，2000，15（1）:363-369.

［13］倪以信，陳壽孫，張寶霖.動態電力系統的理論和分析/現代電力系統叢書［M］.北京:清華大學出版社，2002.

［14］仲悟之.大型電力系統小干擾穩定性分析方法研究和軟件開發［D］.北京:中國電力科學研究院，2005.

［15］NOCEDAL J，WRIGHT S J.Numerical optimization［M］.Springer verlag，1999.

［16］TIKHONOV A N，ARSENIN V Y.Solutions of Ш-posed Problems［M］.VH Winston&Sons，Washington，DC，1977.

［17］唐利民，朱建軍.不適定非線性最小二乘問題的正則化同倫法及其應用［J］.大地測量與地球動力學，2010，30（6）:51-56.

［18］徐忠海.結構特征靈敏度分析若干問題研究［D］.長春:吉林大學，2008.

［19］FOX R L，KAPOOR M P.Rate of change of eigenvectors and eigenvalues［J］.AIAA Journal，1968，12（6）:2426-2429.

［20］CONDREN J，GEDRA T W.Expected-security-cost opti?mal power flow with small-signal stability constraints［J］.Power Systems，IEEE Transactions on，2006，21（4）:1736-1743.

［21］JANKOVIC M S.Exact nth derivatives of eigenvalues and eigenvectors［J］.Journal of guidance，control，and dy?namics，1994，17（1）:834-837.

［22］NELSON R B.Simplified calculation of eigenvector deriva?tives［J］.AIAA Journal，2011，14（9）:823-832.