穩中有變 注重思想——2012與2013年高考廣東卷數列綜合題探析

廣東省惠州學院數學系 林鴻德 （郵編：516007）

數列是初等數學和高等數學的一個重要銜接點，是歷年高考必考的重點內容之一.以近幾年廣東試題看，既有選擇題或填空題，又有綜合題.但是從歷年高考考試情況反映，數列綜合題是大部分考生認為較難的題型.以下通過對近兩年高考廣東卷理科數學數列綜合題進行比較分析，討論高考數列的命題目的和考查意向，希望能給中學數學教學一點啟示.

1 試題呈現

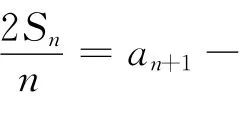
（1）求a2的值；

（2）求數列｛an｝的通項公式；

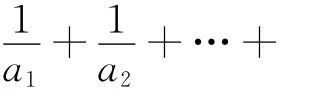
試題2 （2012年廣東卷理數，19）設數列｛an｝的前n項和為Sn.滿足2Sn＝an＋1－2n＋1＋1，n∈N＊，且a1，a2＋5，a3成等差數列.

（1）求a1的值；

（2）求數列｛an｝的通項公式；

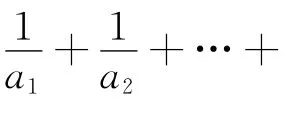
2 解法探析

對于問題1和問題2的第（1）問都較為簡單，目的是為考生增加得分機會，也為后續解答增加信心，體現試題的人文關懷.容易得到試題1中a2＝4及試題2中a1＝1，試題的難點在第（2）問和第（3）問，其中關鍵是對通項公式的求解.

探究1 構造法

根據2an＝2Sn－2Sn－1（n≥2），得

評析 構造法就是在解決某些數學問題的過程中，通過對條件與結論的充分剖析，構造與之相關的輔助模型，使陌生問題轉化為熟悉問題來求解.構造法是解決數列問題的一種重要方法.經常把一個遞推關系式構造成熟悉的等差或等比數列問題來求解數列的通項公式，使問題得到簡化.

探究2 數學歸納法

同理，令n＝2，得a3＝9＝32；

令n＝3，得a4＝16＝42.

猜想：an＝n2.再用數學歸納法證明（略）.

試題2 由條件可得a1＝1；an＋1－3an＝2n，從而得a2＝3a1＋2＝3＋2＝32－22

依此類推，則a3＝3a2＋22＝3（3＋2）＋22＝32＋3×2＋22＝33－23；

a4＝3a3＋23＝3（32＋3×2＋22）＋23＝33＋32×2＋3×22＋23＝34－24.

猜想：an＝3n－2n.再用數學歸納法證明（略）.

評析 數學歸納法是中學數學中一種常用的論證方法.它在一些較難的問題中發揮著重要作用.常用來處理和自然數有關的數學命題.如數列通項公式的求解問題，可通過觀察——歸納——猜想——證明的過程來求解.有利于培養學生觀察、猜想與歸納的合情推理能力.

探究3 放縮法

評析 數列不等式的證明是高中數學教學的重點和難點，也是高考考查的熱點，多數以壓軸題的形式出現.證明此類不等式最常用的方法就是放縮法.在數列不等式的證明中經常把普通數列的求和放縮化歸為等差、等比數列等可求和的數列來求解，這樣就可求出其前n項和，通過這個和的橋梁作用來完成證明.

3 命題分析

從命題角度看，兩道題所考查的基礎知識有所不同，但考查的數學基本思想、基本能力是一致的，注重對分類、整合思想和化歸思想的考查，注重對推理論證能力和運算求解能力的考查，展現了數學的科學價值和人文價值.

（1）分類與整合思想

在數學問題中，有些問題含有多種可能的情況，難以對它進行統一處理時，只能按其出現各種情況分類進行討論，旨在化大為小，化小為了.在數學活動中，分類好比指南針，它能給我們指明方向.分類討論思想貫穿于高中數學的全過程，不僅能迅速地找到解決問題的切入點，還起到了搭建解決問題的總體框架的作用，使人們在清晰的邏輯結構中再逐一地解析每一個具體問題.

在運用數列通項公式與前n項和的關系時，應當討論n＝1和n≥2的情況.就這兩道試題來看，都需要對n進行討論，在形成分類討論的步驟以后，還要切勿忘掉整合這一步.只有完成上述兩步，才算完成了分類與整合的完整過程.這是大部分考生容易出錯的地方，因此，在平時的練習中就應該養成細致認真的好習慣.

（2）化歸思想

在中學數學中，分析、處理和解決問題時，總是將較復雜的問題向易解決的方向轉化，將陌生的問題向熟悉的問題轉化，即化繁為簡、化難為易、化未知為已知等.一般來說，化歸思想主要體現于運用數學方法處理和解決數學問題的過程之中.在數學教學中，充分利用化歸思想，有利于學生構建知識體系，強化其解決數學問題的應變能力，發展其數學思維能力.

在利用構造法和放縮法求解數列問題時，體現的正是化歸思想.在中學數學中，等差數列和等比數列是要求掌握的兩類基本數列，其他的大部分數列都是通過轉化為這兩類數列來處理的.如試題1是轉化為等差數列來求解，而試題2是轉化為等比數列來求解.另外，對于數列的求和，則通過放縮化歸為特殊的數列求和來求解.如試題1將其放縮為兩項的積的形式，再利用裂項相消法求和并完成證明的目的.試題2則是通過放縮化歸為等比數列求和的形式，再利用公式求和.

（3）推理論證能力

推理是思維的基本形式之一，它由前提和結論兩部分組成.論證是由已有的正確的前提到被論證的結論的一連串的推理過程.推理既包括演繹推理，也包括合情推理；論證方法既包括按形式劃分的演繹法和歸納法，也包括按思考方式劃分的直接證法和間接證法.一般運用合情推理進行猜想，再運用演繹推理進行證明.

在運用數學歸納法求解數列通項公式時，先通過數列的前幾項運用合情推理的方法對數列的通項公式進行猜想，然后再運用演繹推理的方法對猜想的通項公式進行證明.這是數列中常用的一種方法，是高中生應當熟練掌握的一種處理問題的方法.

（4）運算求解能力

運算求解能力是思維能力和運算技能的結合.運算包括對數字的計算、估值和近似計算，對式子的組合變形與分解變形，對幾何圖形各幾何量的計算求解等.運算能力包括分析運算條件、探究運算方向、選擇運算公式、確定運算程序等一系列過程中的思維能力，也包括在實施運算過程中遇到障礙而調整運算的能力.

運算求解能力是解決數學問題的基本能力，對它的考查成為高考命題者控制題目難易程序的主要手段.“錯解”往往是“錯算”結出的苦果.在上述試題中要特別注意的是裂項相消法中消去之后剩下的項，這是學生容易出錯的地方.因此，在平時學習中，要求學生會根據法則、公式進行正確運算、變形和數據處理，能根據問題的條件尋找與設計合理、簡捷的運算途徑，能根據要求對數據進行估計和近似計算.

總之，從近兩年高考數列的命題上看，突出基本數學思想方法，強化能力立意，有效地發揮了考試的選拔性功能.

4 教學反思

經過上述分析發現，兩道試題作為高考的綜合題，不需要高深的數學知識和方法就能解決，都是對基本概念、定理和基本思想方法進行考查，以及對綜合分析能力的考查.從高考的命題角度給我們的教學帶來一定的啟示：

（1）重視基礎知識的理解

根據課程標準的要求，堅持了對數學基礎知識、基本技能、基本思想方法的考查，其中強調注重對知識內在聯系的考查，這就要求我們的教學應注意基礎知識的內在聯系.這是不少教師教學中比較缺乏的，易造成教學中重點把握不住，一味地強化訓練，其效果不佳.因此，教師要理解所教基礎知識在高中階段、本章、本節、本課的地位以及重要性，理解所教基礎知識的掌握程度，理解所教基礎知識的多方向延伸的出發點，以及可能的生長方向，做到這樣，基礎知識的訓練才能有度，才能有效，才能達標.

（2）切實認識基本技能的本質

基本技能的水平高低，決定于基礎知識掌握的熟練程度.提高基本技能的運用水平就是多練.但僅是一方面，有時即使練得再多，基本技巧的運用水平還是難以提高.其中主要原因是沒有理解基本技巧的本質，如求解數列的通項公式有很多種方法，如倒數法，很多學生根本不理解倒數法的作用是什么.因此，在教學時，更要注重引領學生理解基本技巧的作用.

（3）滲透數學基本思想方法

高中數學教學是貫穿數學思想方法的教學.數學教育家傅仲孫先生說過：“思想方法為經，教材知識為緯.”在實際教學中，許多教師卻往往忽視數學思想方法的教學，或者覺得太虛空，無法準確把握.這實際上是對數學思想方法認識不到位的體現.學好數學，不等于拼命做習題、背公式，而是著重領會數學的思想方法和精神實質，了解數學在文明發展中所起的關鍵作用，自覺接受數學文化的熏陶.只有這樣，才能從根本上體現素質教育的要求，并為全民族思想文化素質的提高夯實基礎.因此，在教學的過程中，不能只注重解題訓練和題型歸納，要重視對數學思想的培養，它蘊含在數學知識的產生、發展及運用的全過程中，需要在平時教學中時刻滲透，適時地引導學生梳理總結，逐個認識其本質特征和思維特點，主動地、有意地將這些思想方法滲透到解題過程中去.

（4）注重數學能力的提高

命題者以數學知識為載體，從問題入手，把握學科的整體意義，用統一的數學觀點組織材料，側重體現對知識的理解和應用，以此來檢測考生將知識遷移到不同情境中的能力.在教學中，不應追求數學解題中的“技巧”，不搞“偏題”、“怪題”.將最基本的數學方法進行提升和鞏固，突出思維能力和運算能力，及時引申拓展、培養歸納能力，這樣學生在高考中才可以達到融會貫通、高屋建瓴的境界.

總之，在數學教學中，教師應當善于將知識縱橫聯系，加強學生對數學思想的提煉和應用，注重培養學生的思維能力以及分析問題和解決問題的能力.

1 嚴士健.普通高中數學課程標準（實驗）解讀［M］.南京：江蘇教育出版社，2011

2 李善良等.高中新課程問題與對策：數學［M］.上海：上海教育出版社，2012

3 涂榮豹等.新編數學教學論［M］.華東師范大學出版社，2011

4 林生.平穩中重基礎 樸素中透靈氣 常規中見真功——2012年高考數學廣東卷試題評析與備考建議［J］.中國數學教育，2012，20：27－30

5 左偉群，劉秀湘.穩定題型難度，凸顯雙基觀念——2013年高考數學廣東卷試題與答卷分析［J］.中學數學研究，2013，8