幾何相位分析法(GPA)基本原理
郭紅艷
遼寧廣播電視大學錦州分校(錦州 121000)
分析固體物質微觀結構中的應變場,對于豐富人們對微觀世界的認識有著十分重要的意義。獲得該應變場的方法有兩種常用方法:peak-finding(PF)法和geometric phase images(GPA)法。相比而言,材利用高分辨像處理技術分析獲得位移場和應變場大小的幾何相位分析方法,其精度和應用范圍較peak-finding方法更高和更廣泛。其精度可達0.003nm[1],并已用于半導體材料裂紋、位錯和結構合金中小的析出相周圍位移場和應變場的測量[2-4]。GPA方法是M.J.Hytch教授在1998年的Ultramicroscopy雜志上首先提出。由于HRTEM像可以由經過Fourier變換后某一帶軸2維的Bragg反射譜所表征。周期排列的2維強衍射斑點中蘊含晶體結構信息。選擇兩個非線性相關的衍射斑點就可以定義正空間的2維高分辨像,并以此為參考可以度量實驗高分辨像晶格的畸變。
GPA的基本原理:
完整晶體的HRTEM像的強度可以用公式(1)來描述:
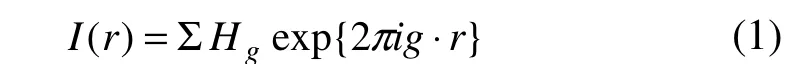
其中: )(rI 表示在位置r處像的強度,g是與布拉格反射點相關的周期性。傅里葉互相關系數gH 可以用公式(2)描述:
其中gA表示振幅,gP表示相位。
為了說明像的強度隨位置的變化而改變,將gH看做位置的函數:
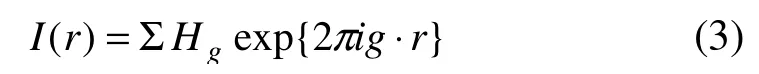
相關系數 )(rHg可以解釋為傅里葉分量gH 的實際值。為了將上述函數用傅里葉空間表達,必須對變換后的強度定義為:
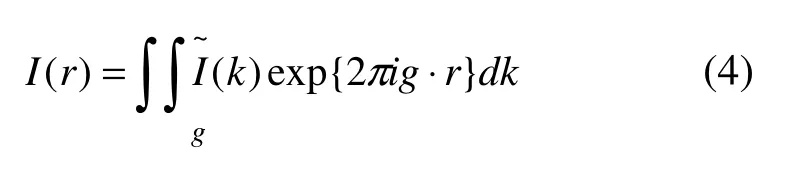
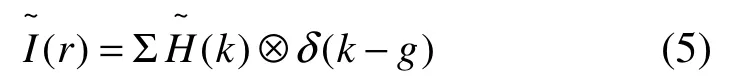
公式(3)的傅里葉變換為:用與倒易空間矢量g的卷積操作表示。對于完
算符表示卷積計算,因此公式(5)說明可以整晶體HRTEM像的傅里葉變換
位置時其值才不為零并且函數是高的δ函,只有其處于布拉格數。如果在圖像某位置有變化,那么在傅里葉變換過程中布拉格衍射位置直接會變成非零。在一個布里淵區,g可以寫成:

這可以引入掩模函數提取相應信息。

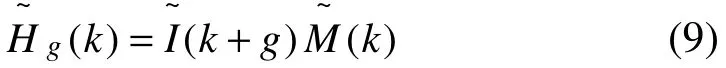
這樣,公式(5)給出的HRTEM像強度的傅立葉變換可以用公式(9)表達出來。
完整晶體高分辨像傅里葉變換分量gH ,強度I( r)分別用來表征與衍射矢量g相對應的高分辨像的
接下來 )(rHg可以按照公式(9)進行定義振幅和相位。按照公式(2)的定義,將公式(1)寫成振幅Ag和相位 Pg的形式,并用該公式用于真實圖像上,考慮到傅里葉變換后圖像存在共軛對稱特性,因而可得公式(10):
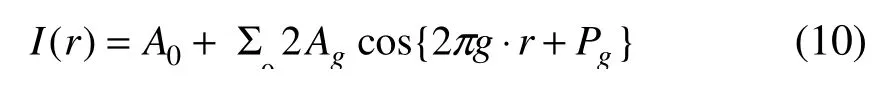
特定晶面的晶格條紋 )(rBg科研用公式(11)描述
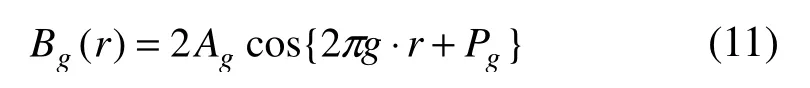
將掩膜板放置于傅里葉變換后的±g衍射矢量位置,可以得到原圖像的布拉格濾波像。在晶格條紋出現變化的時候,在傅里葉變換后的衍射圖中仍保留共軛對稱性:
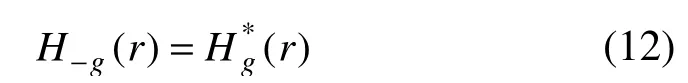
利用公式(7)和(8)定義的布里淵掩膜板過濾得到的布拉格濾波像的強度可以表示為:
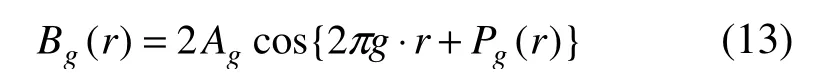
假設倒易空間晶格矢量相對于完整晶體倒易空間矢量發生了改變,既:

式中:gΔ表示在倒易空間中相對于完整晶體的改變量。這樣公式(11)則可以寫成
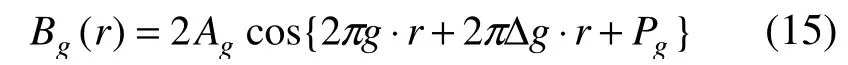
將公式(15)與公式(13)進行比較可知,相位作為位置的函數可以表示為:

忽略任意完整晶體產生的常數相位gP,那么由于倒易空間晶格矢量的變化在相位圖上必定產生位移量的明顯變化。
針對具體的HRTEM圖像,GPA分析的過程是:首先對HRTEM像利用適當的掩膜板濾波后進行傅里葉變換得到含有強度信息的倒易空間的衍射譜;選擇一個衍射斑點作參考的矢量g,利用適當的掩膜板做濾波處理;接著計算原始圖像傅里葉變換后的強度于位置矢量g;進行反傅里葉變換可以計算出

按照公式(2)將 )(rHg寫成振幅和相位形式:

接著按下面公式計算布拉格濾波后的像強度
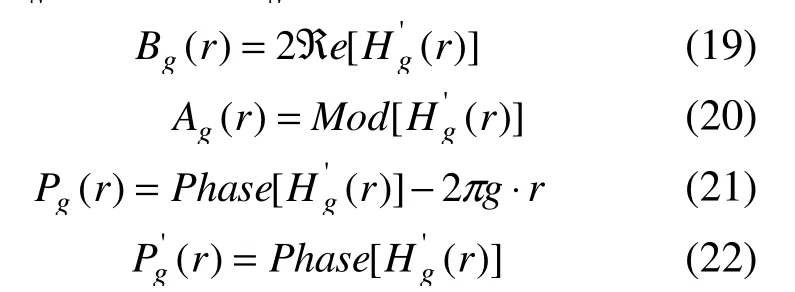
公式中e?表示實部,表示HRTEM像的原始相位,對微分可以得到可用于確定局部倒易空間矢量的改變量將原始相位減去常量)(2rgπ就可以得到)(rPg。
利用兩個線性無關的倒易矢量1g和2g可以確定與之相對的相位 )(rPg。
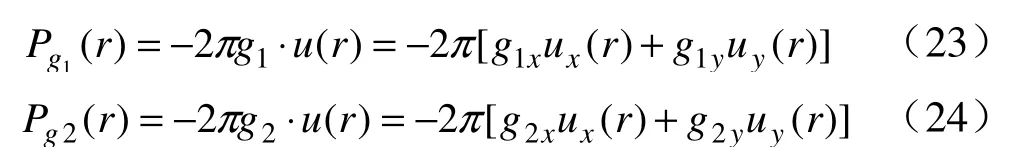
用矩陣方式表示位移場:
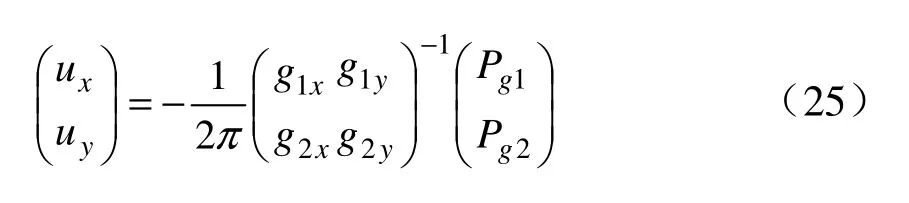
令按照線性代數原理可得T表示矩陣的轉置,帶入公式(25)可得:
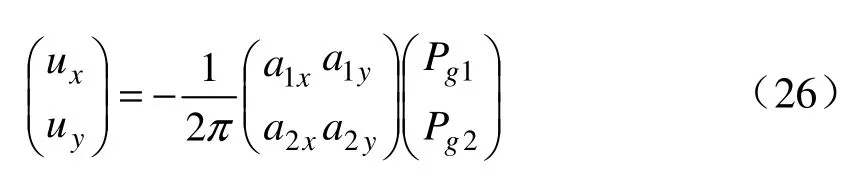
根據彈塑性力學原理將公式(26)求導數,得到應變場大小:
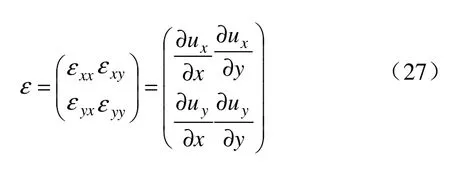
[1]H?tch M J,Putaux J-L,Pénisson J-M.Measurement of the displacement field of dislocations to 0.03? by electron microscopy[J].Nature,2003,423:270-273.
[2]Zhao C W,Xing Y M,Bai P C.Quantitative measurement of deformation field aroundlow-angle grain boundaries by electron microscopy[J].Physica B,2008,403(10-11):1838-1842.
[3]侯小虎,白樸存,趙春旺,邢永明.噴射沉積Al-Zn-Cu-Mg合金GP區應變場的定量測量[J].實驗力學,2011,26(1):16-20.
[4]Zhao C W,Xing Y M,Bai P C.Experimental examination of displacement field in an edge dislocation core in aluminum[J].Physics Letters A,2008,372(3):312-315.
[5]H?tch M J,Snoeck E,Kilaas R.Quantitative measurement of displacement and strain fields from HREM micrographs[J].Ultramicroscopy,1998,74:131-146.

