增刪點后的Voronoi圖生成算法
張 娟, 杜全葉
(1. 蘭州交通大學,甘肅 蘭州 730070;2. 中國測繪科學研究院,北京 100380)
1 Voronoi圖的基礎
1.1 Voronoi 圖的概念[1]
如圖1,L是P1P2的垂直平分線,并將平面分成L左和L右兩部分,位于L左內的點P左 具有特性:
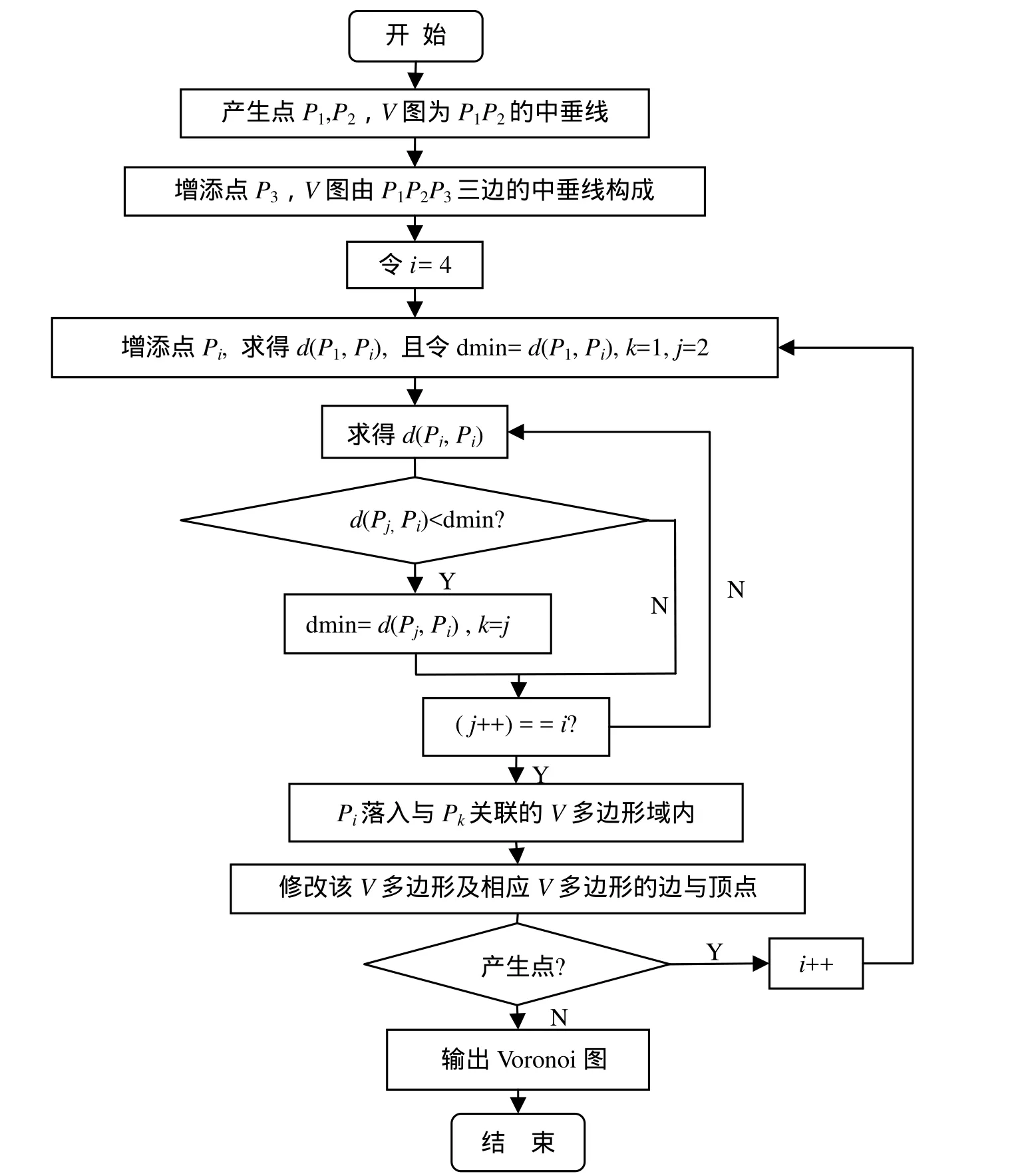
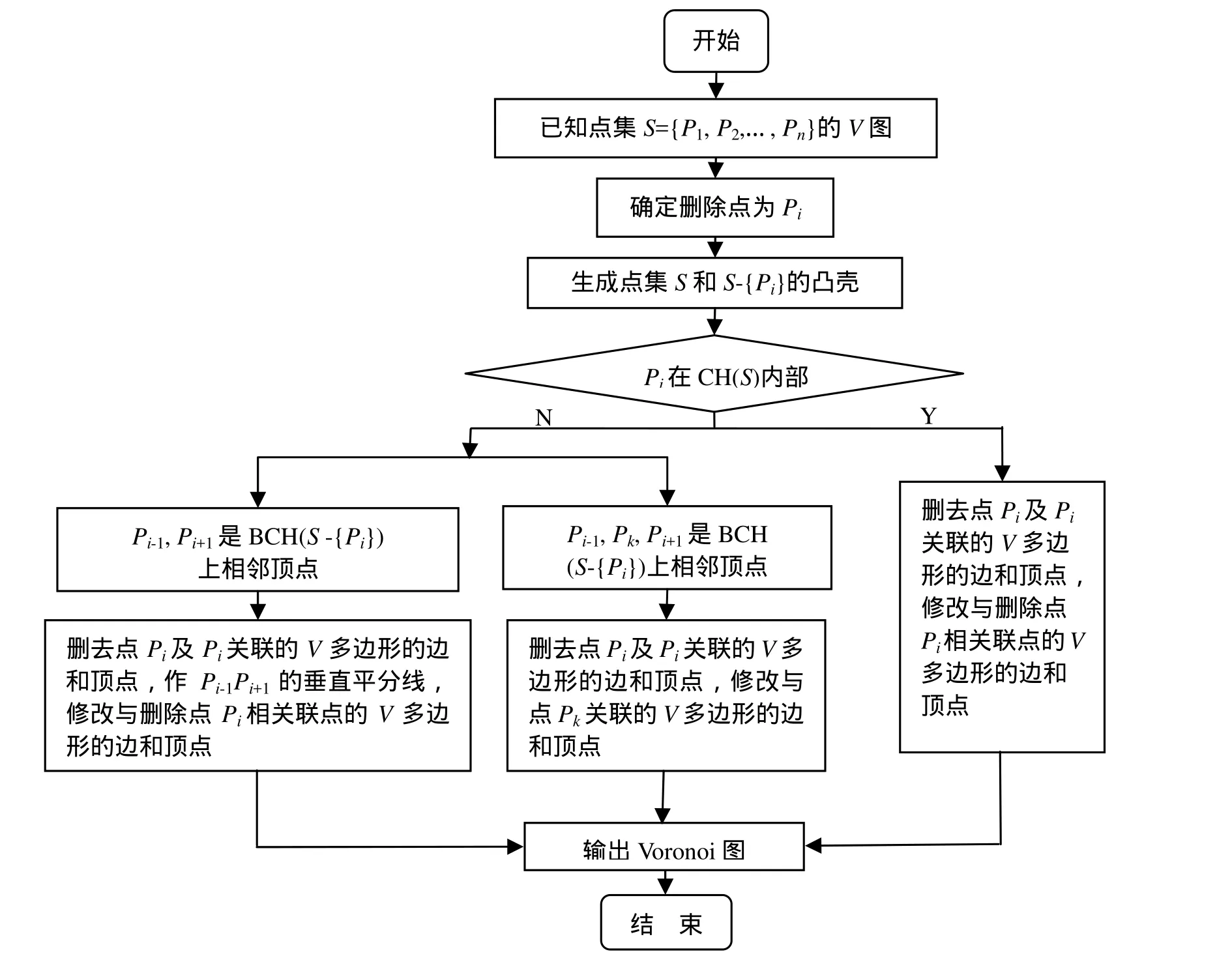
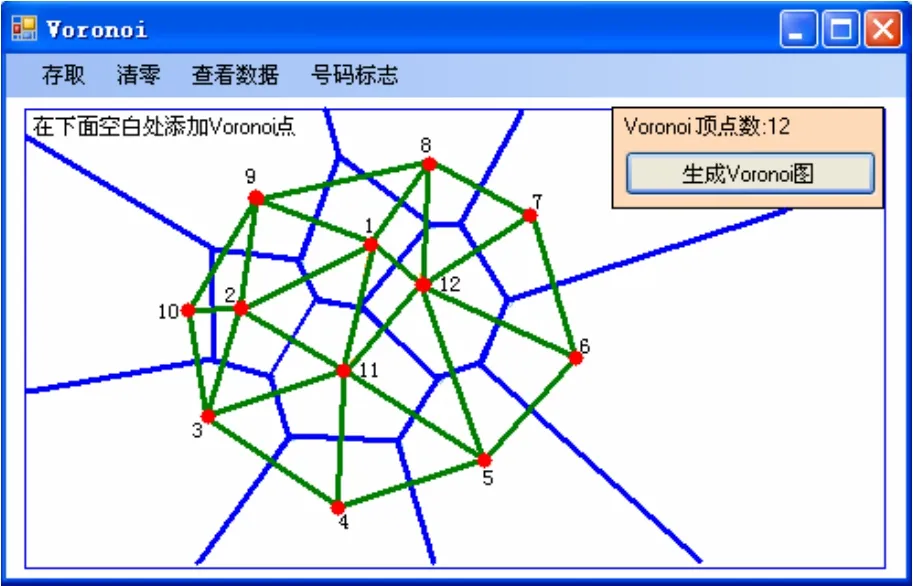
d(P左,P1) 圖 1 V(P1),V(P2)圖示 圖2 n= 6時的一種Voronoi圖 給定平面上n個點的點集S={P1,P2,…,Pn},定義V(Pi)=H(Pi,Pj),即V(Pi)表示比其他點更接近Pi的點的軌跡是n-1個半平面的交,它是一個不多于n-1條邊的凸多邊形域,稱為關聯于Pi的Voronoi多邊形或關聯于Pi的Voronoi域。 S中的每個點都可做一個 Voronoi多邊形,這樣的n個多邊形組成的圖稱為Voronoi圖,記作Vor(S),其頂點和邊分別稱為Voronoi頂點和Voronoi邊,如圖2為n= 6時的一種Voronoi圖。Voronoi圖的定義可以推廣到三維或多維,也可以推廣到二階或高階(以2個站點或多個站點為一組來劃分臨近區域)[2]。1.2 Voronoi 圖的特性 1) 每個Voronoi多邊形內僅含有一個離散點數據; 2) Voronoi多邊形內的點到相應離散點的距離最近; 3) 每個Voronoi 點恰好是3條Voronoi 邊的交點(Voronoi 點是S中3點形成的三角形的外接圓的圓心)。 簡單來說,Voronoi圖是一個關于空間劃分的基礎數據結構[2],已知平面上有任意n個點,按照這些點的分布將平面劃分成n部分,從而得到一種對平面的劃分圖。Voronoi圖理論成功地解決了找最近點、求最大空圓、求n個點的凸包、求最小樹等問題,與其對偶圖Delaunay三角剖分已被廣泛地應用到幾何形體重構、計算機圖形學、圖像處理、模式識別、機器人運動規劃、分子生物學等眾多領域。 隨著計算機的發展和工程設計自動化的要求以及建立地理信息系統的需要,出現了用數字形式表示地面的方式,即“數字地面模型(DTM)”。而數字高程模型(DEM)中地表面形態只用點的高程來表示,具有存儲量小,可以進行壓縮,便于使用管理的優點,是目前使用最廣泛的地形模型[3]。DEM 中不規則三角網 TIN的建立和優化是地圖正射影像的一個基礎研究問題,其要求所建的TIN模型具有存儲效率高、數據冗余度小、圖形網格強度好、三角網拓撲關系強、且能較好地顧及地形特征等優勢。用Voronoi圖及其對偶圖 Delaunay,發展了帶約束的D-網特征建模,充分地考慮了地形特征(如地性線、陡坎、地物地貌等)[4]。 平面點集的Voronoi 圖構造算法有多種:半平面的交、增量構造方法、分治法、減量算法、平面掃描算法等,由于增量算法不僅適用于靜態點集,而且還適用于動態點集,因而受到重視[5]。本文為了方便實現增刪點式Voronoi 圖的動態生成,選用了聯機增量和減量算法。 已知點集S={P1,P2,…,Pn},并設已經構造出k(k 算法中分別計算了Pi至P1,P2,…,Pi-1的距離,并相互比較求得與Pi最近的點,因此需要進行i-1次的距離計算和i-2次的距離比較。因為n個點的Voronoi圖至多有3n-6條邊和2n-5個頂點,所以每個V多邊形邊的數目為一常數,修改與Pi關聯的Voronoi多邊形邊與頂點時,其邊數決定了計算的復雜性,即耗費常數時間[1]。 已知點集S={P1,P2,…,Pn}的Voronoi圖,現刪除點Pi之后,要求構造Voronoi圖Vor({P1,P2,…,Pi-1,Pi+1,…,Pn}),算法流程圖如圖4所示。 圖3 聯機增量算法流程圖 執行該算法時,首先判定點Pi是否為凸殼頂點或在凸殼內,這需要求出凸殼CH(S)進行比較,耗時為O(nlogn)。如果點Pi-1,Pi,Pi+1是凸殼邊界BCH(S)上連續的3個點,刪除點Pi后耗費O(log2n)時間可以恢復 BCH(S-{Pi}),即判定Pi-1與Pi+1之間是否有新的凸殼頂點。刪去點Pi及Pi關聯的Voronoi多邊形的邊和頂點,修改相應的Voronoi多邊形的邊和頂點,耗費常數時間。因此算法的時間復雜度為O(nlogn)[1]。 在程序設計中,數據類型定義的好壞對程序設計的影響是很大的,良好合理的數據類型定義,將極大地方便程序中數據的處理,本文根據Voronoi邊和頂點在數據文件中的存儲方式定義及其相應的數據結構,對其定義如下: 其中x,y為Voronoi點的位置坐標,next為指向下一個點數據的指針,點和點之間以此指針相連形成單向鏈表,從而構成Voronoi圖(圖5為任意添加12個Voronoi頂點后,算法運行得到的結果)。 圖4 減量算法流程圖 圖5 實驗結果 Voronoi 圖是計算幾何學科的一個重要結構,它與一些自然結構十分相像,已廣泛應用于天文、地理、網絡等領域[6]。隨著計算機技術的普及和發展,Voronoi 圖的應用范圍也在不斷擴大,可將其擴展到三維,用于DTM的建模等。本文實現了增刪點后Voronoi圖的生成,所選用的算法還存在著不足,需進一步改進: 1) 增量算法中每次增加點Pi需要進行i-1次的距離計算及i-2次最小值比較,循環耗時。 2) 執行減量算法時,每刪除一個點就要對與之關聯的Voronoi多邊形邊和頂點進行修改,修改量大,影響算法效率。 [1]周培德. 計算幾何——算法設計與分析[M]. 北京:清華大學出版社, 2005: 88-101. [2]劉金義, 劉 爽. Voronoi 圖應用綜述[J]. 工程圖學學報, 2004, 25(2): 125-132. [3]李德仁, 周月琴, 金為銑. 攝影測量與遙感概論[M].北京: 測繪出版社, 2001: 163-164. [4]彭儀普, 劉文熙. Delaunay三角網與 Voronoi圖在GIS中的應用研究[J]. 測繪工程, 2002, 11(3): 39-41. [5]王曉東, 廖士中. 一個基于桶技術的平面點集Voronoi 圖增量算法[J]. 遼寧師范大學學報(自然科學版), 2002, 25(2): 139-143. [6]秦志霞, 沈 煒, 劉文昊. 二維 Voronoi 圖刪除任意生成點算法研究[J]. 浙江理工大學學報, 2010,27(3): 421-425.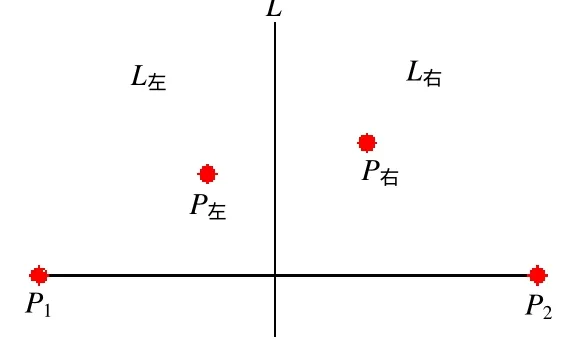
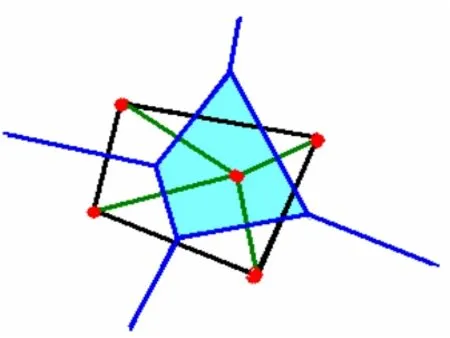
1.3 Voronoi 圖的應用
2 Voronoi 圖生成算法
2.1 聯機增量算法
2.2 減量算法
3 數據類型定義

4 結 論

