含膠結物砂質邊坡穩定性的新分析方法
潘 健,丁孝勇
(華南理工大學土木與交通學院,廣東 廣州 510640)
0 引言
隨著世界沿海建設的不斷發展,在我國沿海建設過程中,特別是長江中下游和南方沿海地區以中、細砂、粘性土為主的河流沖積平原為主,如廣州,上海等地[1].經常面臨分析含有膠結物的砂質邊坡穩定性的問題,因此建立一種合理的分析含膠結物砂質邊坡的方法十分迫切.
近年來許多國內外的學者對膠結物顆粒的巖土特性做了大量的研究,對于膠結砂土顆粒間膠結接觸模型問題,Cundall提出標準接觸模型用于分析顆粒介質的力學特性[2];蔣明鏡提出簡單膠結模型(即蔣氏模型)[3],并在該模型下才有PFC2D軟件對膠結砂土進行雙軸實驗模擬[4],同時蔣明鏡還研究不同膠結厚度和膠結物類型下,粒間膠結強度指標的變化規律以及對膠結物力學特性的影響[5-6];張永雙對砂黃土的膠結物組成及膠結機理進行了研究[7];Clough通過大量實驗來研究膠結砂的抗拉強度和壓縮特性[8],三軸試驗和循環剪切實驗測定弱膠結砂的膠結程度和重度[9];Nicholas Sitar采用實地觀察和有限元分析程序研究含膠結物砂質邊坡在地震響應下的變形特征和破壞[10];Hampton通過案例分析含膠結物砂質邊坡在自然狀態下土體內應力和土體參數變化[11].這些研究包括含膠結物砂土顆粒間的接觸模型、強度特性、抗液化能力、邊坡的變形、破壞特征和在自然狀態下應力特征和土體參數變化;但是這些研究在預測邊坡發生破壞的準確程度方面也未能達到令人滿意的效果.并且在實際工程中,對如何準確評價含膠結物砂質邊坡穩定性缺乏較可靠的理論指導.在某些情況下,常規的分析方法[12]對邊坡穩定性的分析給出了保守的估計;一些邊坡理論上會發生破壞而實際觀測中是穩定的;而一些邊坡常規方法分析結果是穩定的,但實際上發生了破壞.
為了更好的反映膠結程度及幾何形狀對沿海邊坡穩定性的影響,給出與所觀察到的邊坡破壞結果相一致的分析方法.本文根據膠結程度的不同將含膠結物邊坡分類,分析它們的破壞模式,根據破壞模式尋求不同的穩定性分析方法.
1 含膠結物砂質邊坡破壞模式分析
要準確評價含膠結物砂質邊坡的穩定性,首先要正確的鑒定邊坡的破壞模式.沿海邊坡在自然界中經歷一系列的侵蝕作用,包括地表風化[13]、地表水和地下水滲流[14]、坡腳腐蝕[15].每一個過程都對應著特定的破壞模式(平面剪切、旋轉剪切、旋轉張拉等),需要不同的分析方法,因而邊坡的破壞模式決定著邊坡穩定性分析方法的準確性.然而具體的破壞模式又與邊坡精確的幾何形狀和材料性能相關.
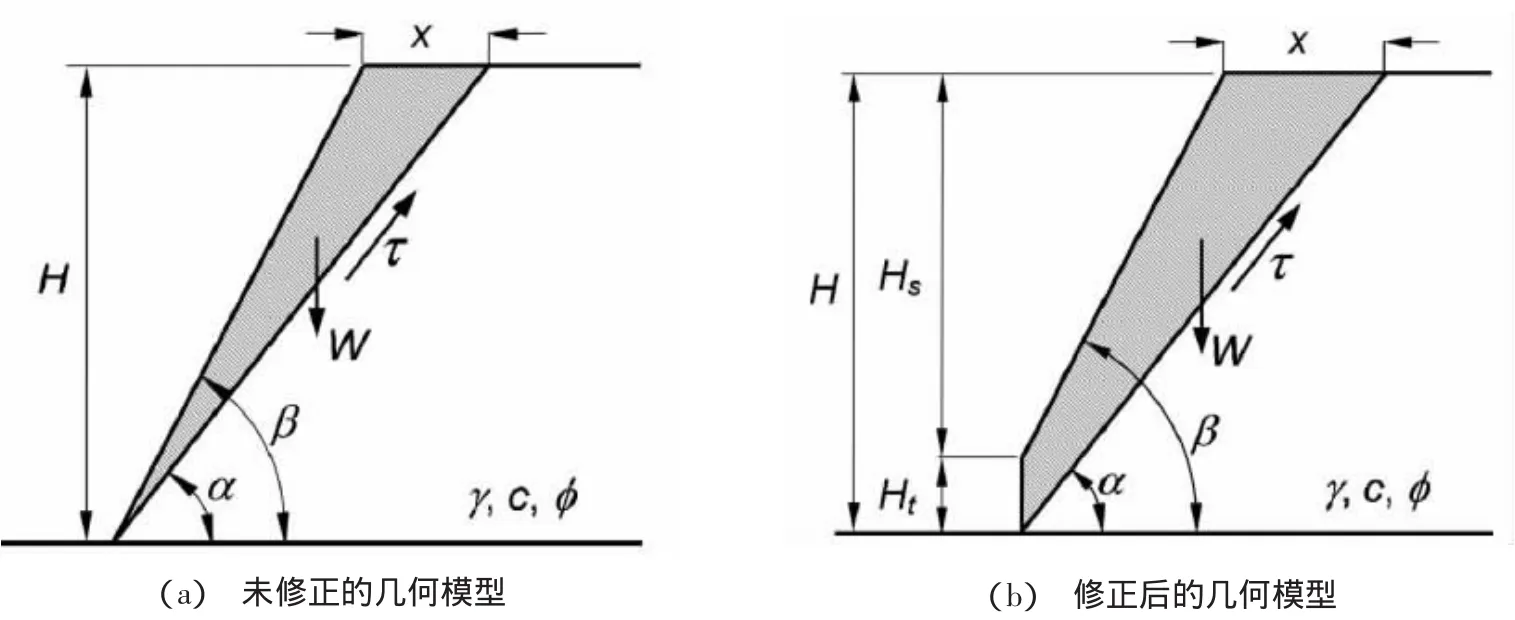
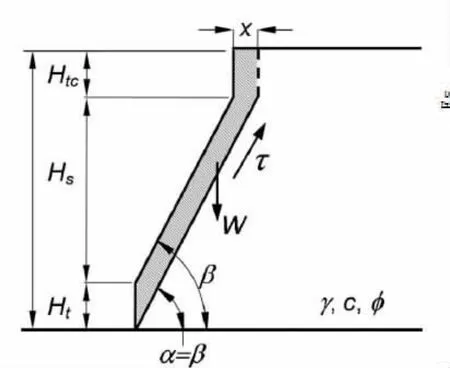
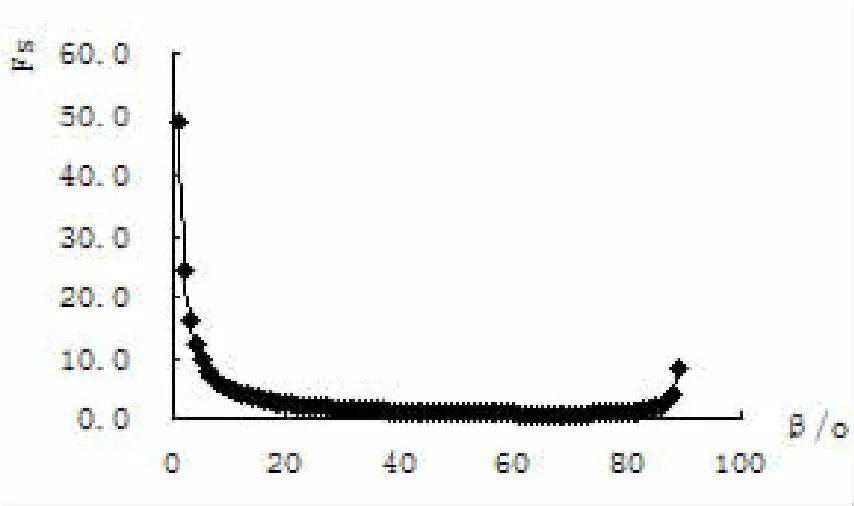
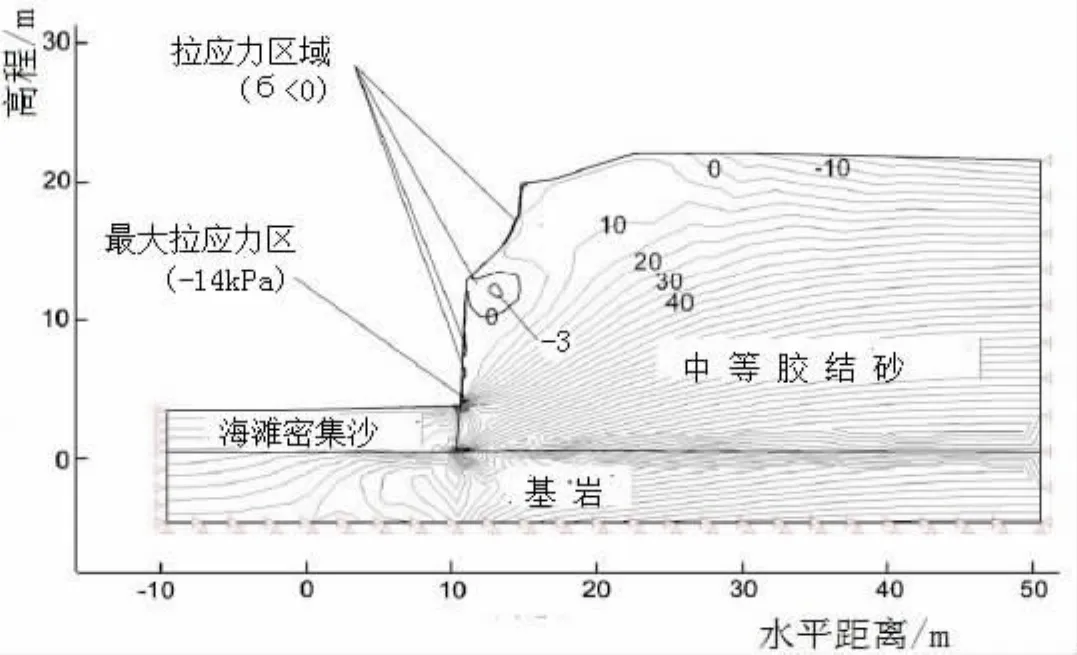
對某一區域膠結砂質邊坡破壞模式的分析[13]顯示:不同膠結程度的砂質邊坡存在不同的破壞模式;其中含弱膠結物的砂質邊坡(無側限抗壓強度qu<30 kPa),由于各種腐蝕作用,邊坡幾何形狀發生變化,邊坡破壞平面平行于邊坡坡面;含中等膠結物的砂質邊坡(無側限抗壓強度30 kPa 由分析結果可見,對于含膠結物的砂質邊坡的破壞模式隨著膠結程度發生變化的,不同膠結程度的邊坡的破壞模式不同,因而穩定性分析方法也會不同. 在邊坡穩定性分析中經典的分析方法是利用極限平衡方程或者連續變形協調方程,但在具體的邊坡穩定性分析中選擇何種方法依賴于材料的性能.例如對于發生很小的應變就發生破壞的邊坡,常選用極限平衡法.常規的分析方法適用于弱膠結物砂質邊坡的破壞模式.常規分析方法[12]假定土體沿莫爾-庫倫剪切面滑動,假定破壞平面的角度α=(β+φ)/2,其模型如圖1(a)所示,其中陰影部分滑動楔形體的重力W為: 抗滑動力T為: 其中L=H/sinα,c為土體的粘聚力,?為土體的內摩擦角,γ為土體的重度,β為邊坡傾角,α為破壞平面的傾角,則坡頂水平張拉裂隙水平位置x為: 安全系數Fs表達式為 當邊坡的傾角越大這種方法預測的結果越準確,特別是對于接近垂直的粘性土邊坡[13].然而將這種方法應用于含弱膠結物砂質邊坡穩定性分析時,計算所得到坡頂裂隙水平位置x超過了預測值的2~3倍,破壞時邊坡的角度高估了10°. 考慮到邊坡由于水流的沖擊作用而存在垂直坡腳,為了更加準確的模擬邊坡的幾何形狀,有學者對常規的方法進行了修正[15].修正的方法假定存在垂直坡腳,設垂直坡腳高度Ht,邊坡的總高度H等于Ht和Hs之和,如圖1(b)所示,修正后的表達式如下: 其中坡頂水平張拉裂隙位置x為: 圖1 常用方法的幾何模型 楔形滑動體的重力W為: 安全系數可以表示為如下形式: 修正后的表達式雖然在預測坡頂裂隙水平位置有所改善,能夠更好的模擬邊坡幾何形狀在發展過程中的真實狀況;但它忽略了邊坡存在垂直坡頂的可能,并且坡頂張拉裂隙水平位置的估計仍比預測值大很多,對于破壞平面角度的預測也不準確[16].同時,由于假定條件的限制,該方法只能適用于β>?的邊坡.另外,這兩種分析方法是以剪切破壞模式為主,無法分析以拉伸破壞為主的含中等膠結物砂質邊坡. 由于常規的分析方法和修正后的方法存在一定的缺陷,為了準確的估計邊坡破壞角度和坡頂張拉裂隙的水平位置.改進的方法準確的考慮邊坡傾角、破壞平面傾角、弱膠結程度砂質邊坡坡腳幾何形狀對穩定性的影響.該方法允許坡腳高度的變化,考慮垂直坡頂的存在,假定邊坡破壞平面的傾斜角度平行于邊坡坡面傾角(即α=β),且邊坡無限大,建立極限平衡方程.其幾何模型如圖2所示,陰影區為滑動楔形體的重力(W). 坡頂裂隙水平位置x為 抗滑力T的表達式見等式(2),安全系數可以表示為 式中H為邊坡的總高度,Htc為坡頂垂直高度,γ為總重度.注意當等式(10)中Ht=0,Htc=0(即H=Hs),且α不等于β時,可以得到等式(2).但是要使Ht的值非零,必須假定存在不連續的破壞深度.等式(10)可以用來判別邊坡是否達到破壞所需要的幾何條件.也就是說,邊坡達到極限平衡狀態時,Ht,Hs,β的值以及垂直張拉裂縫的位置(見圖2,x).這種方法可以用于快速評價邊坡的穩定性,特別是對于超長邊坡. 對含中等膠結物砂質邊坡的實測分析可知由于邊坡的坡度變陡和地表水、地下水的浸潤作用導致土的抗拉強度降低是邊坡發生破壞的主要原因[17].因此對于含弱膠結物砂邊坡的穩定性分析方法不適用于含中等膠結物邊坡.盡管極限平衡分析可以適用于脆性破壞,但是它無法明確確定近乎垂直邊坡的拉應力,故對含中等膠結物砂質邊坡給出不同的穩定性分析方法,即線彈性有限元法.線彈性有限元法可以用來分析邊坡表面的應力,并且可以將表達式寫成與極限平衡法一樣的形式. 線彈性有限元分析法直接比較給定邊坡的表面的拉應力(σ3)和土體的抗拉強度(σt)的大小,當土體抗拉強度(σt)大于邊坡的拉伸強度(σ3)認為邊坡是穩定的,其中σ3<0, 存在兩種可能不穩定的情況:(1)邊坡的幾何形狀發生變化,拉應力增加:(2)材料的抗拉強度降低,例如,由于水的浸潤作用的結果,材料的抗拉強度降低. 由公式可知邊坡坡度增加導致邊坡拉應力增加和由于水的侵蝕作用引起的抗拉強度降低均可以用線彈性有限元法進行分析.等式(12a)和等式(12b)兩種機理都可以引起含中等膠結物砂質邊坡的破壞;但在由于坡腳腐蝕邊坡坡度增加的情況中(如小溪的河岸、沿海峭壁或者其它開挖邊坡),第一種破壞機理在邊坡中更加常見.盡管中等膠結砂邊坡的拉伸破壞,可以用線彈性有限元法分析出邊坡表面的應力分布,但它仍屬于極限平衡分析,并且對所觀察到邊坡發生破壞的行為給出了合理的解釋.這相對于常規的分析方法來說是一種進步. 針對不同膠結程度的沿海砂質邊坡分別給出根據不同案例用新的方法進行分析,并評價改進方法所得到的分析結果的合理性和有效性. 假定含弱膠結物砂質邊坡的材料參數和幾何參數為γ=16.8N/m3,?=36°,c=10 kPa,H=28 m,Ht=4 m,Htc=3 m,β從0°到90°不斷變化代入公式(10)進行計算,其中計算結果如圖3所示.由圖可知隨著β<60°不斷增大,其中表達式(10)中邊坡的安全系數越來越小,當β>60°時,由公式(10)可知,分母逐漸趨近于零,故安全系數又逐漸增大.其中當β=0°表示一平坡,剪切面無切應力安全系數無窮大;當β=46°時,安全系數Fs=1.0,坡頂裂隙值x=3.9 m;當β=90°,表示為一直立邊坡,剪切面無正應力.對于高陡峭邊坡,邊坡發生破壞的模式發生改變,使用該方法無法解釋邊坡的安全性,但可以用來計算邊坡的幾何特征. 圖2 含弱膠結物砂質邊坡模型 圖3 安全系數與邊坡傾角的關系 同理將邊坡的材料和巖土參數代入常規方法(即等式4)和修正后的方法(等式7),將這兩種方法所計算的結果與其它方法相比較如表1所示,改進的方法所得的結果與上限極限分析結果近似相等,而常規的方法和修正后的方法對于邊坡破壞時邊坡的傾角估計與上限極限分析結果相差很大,見表1所示. 表1 含弱膠結物砂質邊坡的不同分析方法結果對比 其中極限上限分析根據莫爾庫倫準則和塑性流動準則,假定形成兩個獨立的剛體滑動面,其表達式為:極限上限分析反映邊坡的真實受荷載情況.因而該方法能夠更加準確的預測邊坡發生破壞時的幾何形狀的變化. 對于含中等膠結物砂質邊坡,引用某沿海邊坡案例[17],用MIDAS/GTS將土層分三種材料,972個節點,847個單元來模擬,每個單元的高度為1.2 m.材料參數和抗拉強度見表2所示,且中等膠結砂在不排水情況下的γsat=19.6 N/m3,?=47°,c=34 kPa[18]. 表2 含中等膠結物砂質邊坡材料特性 線彈性分析結果(圖4)所示坡頂裂隙部位和邊坡表面大部分處于拉伸狀態,坡頂裂隙雖然沒有導致邊坡破壞,但其促使土體的整體強度降低;另外它增加了地表水通過裂隙流入邊坡的潛在可能性.在邊坡表面預測的拉應力為-3 kPa,到底部增加到-14kPa.根據等式(11)和(12),邊坡在干燥狀態下的抗拉強度為32 kPa,遠遠大于邊坡表面的拉應力,故邊坡是穩定的;在濕潤狀態下,抗拉強度小于邊坡拉應力,由等式(12b)可知邊坡失穩.所得到的結果與實際觀測到的邊坡幾何形狀發生的變化相一致. 圖4 含中等膠結物砂質邊坡的應力分布 (1)根據膠結程度將砂質邊坡進行分類,可分析出它們的不同破壞模式.其中含弱膠結物砂質邊坡的破壞模式一般屬于剪切破壞,含中等膠結物砂質邊坡一般為拉伸破壞. (2)常規的分析建立的模型忽略邊坡垂直坡腳和垂直坡頂的存在,分析的結果對于破壞時邊坡的角度高估10°,拉裂縫的水平位置比實際值大2~3倍;修正后的方法不考慮垂直坡頂的存在,與實際情況相差較大.改進的模型考慮了垂直坡頂的影響. (3)對于含弱膠結物砂質邊坡,改進方法假定邊坡發生破壞時的傾角平行于邊坡坡面傾角,建立極限平衡方程.分析結果與極限上限分析的結果基本一致,能夠反映邊坡的真實荷載情況.對于含中等膠結物砂質邊坡,用線彈性有限元法分析出邊坡表面的拉應力分布,直接與邊坡材料的抗拉強度相比較,進而判別邊坡的穩定性.改進方法較合理解釋了邊坡的破壞現象,且可快捷、有效地評估這類邊坡的穩定性. [1]臧秀平,李廣杰,劉寶國.工程地質[M].北京:高等教育出版社,2009. [2]Cundall P A,Strack O D L.A discrete numerical model for granular assemblies[J].Geotechnique,1979,29(1):47-65. [3]Jiang M J,Leroueil S,Konrad J M.DEM study of microstructured soil[C]//55th CSCE-ASCE Conference.HamiLton,2002:313-320. [4]蔣明鏡,張伏光,孫渝剛,等.不同膠結砂土力學特性及膠結破壞的離散元模擬[J].巖土工程學報,2012,34(11):1969-1976. [5]蔣明鏡,周雅萍,陳賀.不同膠結厚度下粒間膠結力學特性的試驗研究 [J].巖土力學,2013,34(5):1264-1273. [6]周雅萍,蔣明鏡,陳賀.變膠結厚度下膠結顆粒微觀模型的初步研究[J].地下空間與工程學報,2011,7(5):890-894. [7]張永雙,曲永新.陜北晉西砂黃土的膠結物與膠結作用研究[J].工程地質學報,2005,13(1):18-28. [8]Clough G W,Rad N S,Bachus R C,et al.Cemented sands under static loading[J].Journal of the Geotechnical Engineering Division,1981,107(6):799-817. [9]Clough G W,Iwabuchi J,Rad N S,et al.Influence of cementation on liquefaction of sands[J].Journal of Geotechnical Engineering,1989,115(8):1102-1117. [10]Sitar N,Clough G W.Seismic response of steep slopes in cemented soils[J].Journal of Geotechnical Engineering,1983,109(2):210-227. [11]Hampton M A.Gravitational failure of sea cliffs in weakly lithified sediment[J].Environmental&Engineering Geoscience,2002,8(3):175-191. [12]Coulomb C A.Essai sur une application des règles de maximis&minimis à quelques problèmes de statique,relatifs à l'architecture[M].De l'Imprimerie Royale,1973,7:343-382. [13]Carson M A,Carson M A.The mechanics of erosion[M].London:Pion,1971. [14]Norris R M,Back W.Groundwater Geomorphology:the role of subsurface water in earth-surface processes and landforms[M].Geological Society of America,Boulder,Colorado.1990.283-290. [15]Sunamura,T.A predictive model for water-induced cliff erosion,with application to pacific coasts of Japan[J].Geological,1982,90:167-178. [16]Darby S E,Thorne C R.Development and testing of riverbank-stability analysis[J].Journal of Hydraulic Engineering,1996,122(8):443-454. [17]Collins B D,Sitar N.Processes of coastal bluff erosion in weakly lithified sands,Pacifica,California,USA[J].Geomorphology,2008,97(3):483-501. [18]Collins B D,Sitar N.Geotechnical properties of cemented sands in steep slopes[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(10):1359-1366.2 含膠結物砂質邊坡破壞模式分析



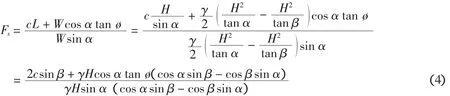

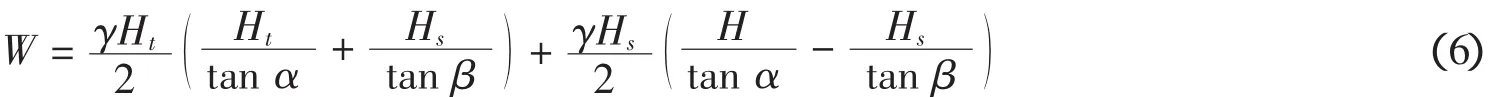

3 穩定性分析方法的改進
3.1含弱膠結物砂質邊坡



3.2 含中等膠結物砂質邊坡



4 工程算例
4.1 含弱膠結物砂質邊坡分析


4.2 含中等膠結物砂質邊坡分析

5 結論

