梯度計算的集合變分方案及其在大氣Ekman層湍流系數反演中的應用*

韓月琪 鐘中 王云峰 杜華棟

1 引言

由于人類活動主要位于大氣邊界層中,而且邊界層中湍流輸運作用對地-氣物質能量循環起著至關重要的作用,因此各種時空尺度的大氣模式和污染物擴散模式都必須要對大氣邊界層問題進行足夠精確的刻畫.大氣湍流問題是一個遠未解決的自然科學難題,所以大氣邊界層數值模擬和業務數值預報模式以及許多研究工作對于湍流摩擦這一物理過程均采用了經驗參數化的方法,即根據大量試驗給出大氣湍流系數的某種經驗形式[1-3].事實上,湍流系數是一個很難確定的物理參數,它與大氣的動力、熱力結構密切相關.因此給出大氣湍流系數合理的計算方法無論對于發展理論研究還是改進業務數值天氣預報、污染物擴散計算都是非常迫切和重要的.

實際上,完全可以把確定邊界層湍流系數的方法視為一個反問題,即在知道部分風場觀測資料的前提下,根據一定的邊界層模型來反演湍流系數.反演方法與技術在目標識別、探地雷達、地球物理遙感、醫學成像、無損檢測等許多領域得到了不同程度的應用,且其研究與開發的前景廣闊[4-15].

本文基于牛頓迭代優化反演方法,將集合計算和變分法結合起來,提出了一種目標函數梯度計算的集合變分方案,實施起來簡單、方便,并根據正演模式的線性化情況提出了兩種計算流程.這種梯度計算方案也可應用于最速下降法、共軛梯度法、變尺度法、組合法等反演方法.在理論推導工作的基礎上,本文利用模擬觀測資料對大氣邊界Ekman層的湍流系數進行了反演試驗,并對反演結果進行了討論分析.為實際應用觀測資料反演Ekman層湍流系數提供了理論基礎與技術保證.

2 梯度計算的集合變分方案

根據觀測資料和物理約束來反演未知參數.首先根據最小二乘原理,建立將未知參數作為控制變量的目標泛函,然后計算目標泛函對于控制變量的梯度,采用優化迭代,使目標泛函達到極小值.

2.1 目標泛函

狀態空間表示為S∈RNs,其中Ns表示狀態維數,x∈S為狀態向量.設正演模式為

其中y是模式輸出值;x為模式輸入值,除已知值外,在此特指控制變量或待反演參數;M為物理模式.對于(1)式,普遍講,由x求y就是正演;而由y求x即是反演.利用y的觀測資料yobs對未知參量x進行反演,目標泛函取為

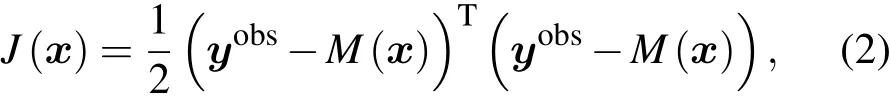
其中上標T表示矩陣轉置.當泛函J的值越小,表明采用反演值計算的模式輸出值與觀測值的一致程度越高;同時說明反演得到的參數越準確.反演的最終目的是在反演參數滿足物理模式(1)式的條件下,使目標泛函(2)式達到極小值.為了使用物理反演算法,采用優化迭代得到反演參數,需要計算目標泛函對于控制變量的梯度.

2.2 梯度的集合變分計算

為了采用集合變分方案計算目標函數對于控制變量的梯度,這里有一系列的未知參數狀態向量用來集合預報,其中NE為集合數.初始未知參數猜值的狀態向量表示為 x0,假設初始猜值的誤差滿足高斯分布[16],NE個未知參數狀態向量為其中

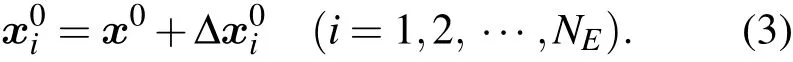
將NE+1個未知參數狀態向量代入正演模式M進行集合計算,可以得到NE+1個模式輸出向量,表示為

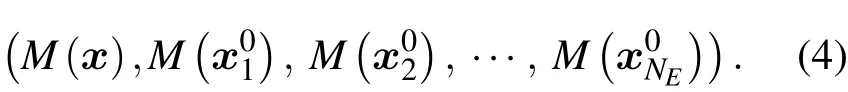
未知參數的反演值x可以寫成初始猜值x0和訂正值之和,訂正值屬于子空間A[17],

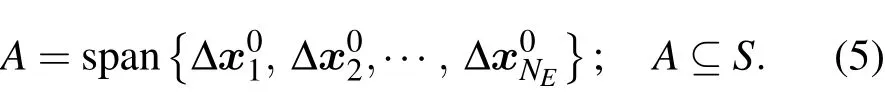
x-x0∈A可以表示為線性組合

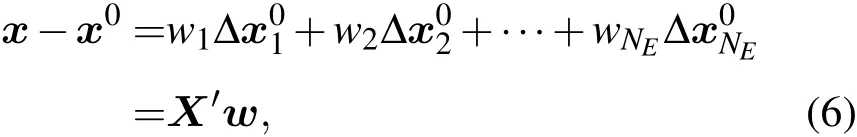
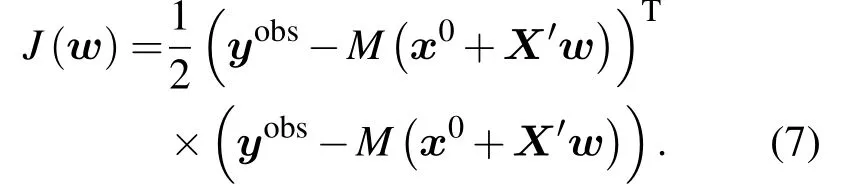
定義新息(innovation)

則

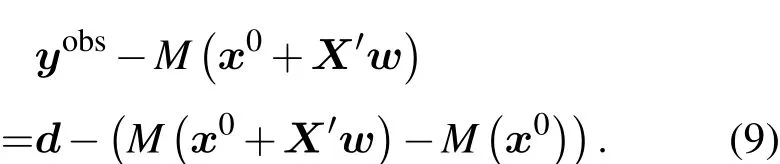
在M可微的情況下,

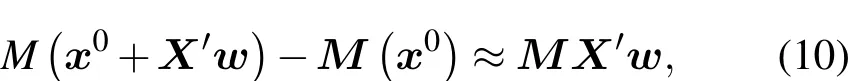
其中M是正演模式M的切線性算子.將(9),(10)式代入(7)式可以得

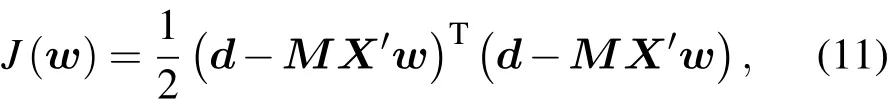
可以求得目標泛函(11)式對控制變量w的梯度

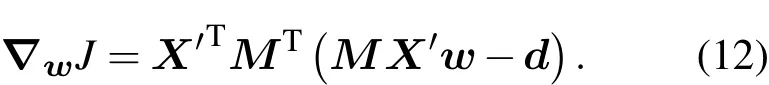
但在(12)式中必須要用到正演模式M的切線性算子M及其伴隨模式MT,為了避免使用伴隨模式,(12)式變為

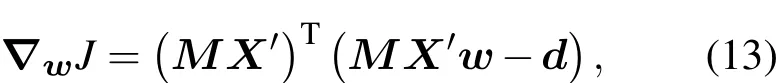
采用集合預報結果,可以采用近似計算方法：

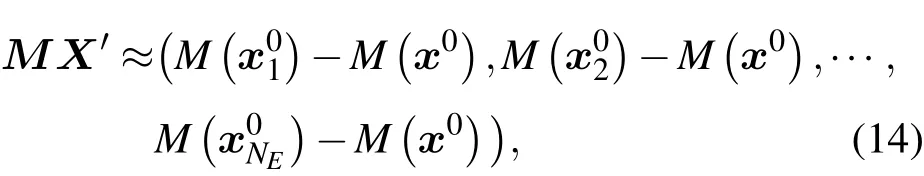
這樣就避免了使用切線性算子M及其伴隨模式MT,從而求得?wJ.采用優化迭代算法,得到J(w)達到極小時的w代入(6)式,便可得到未知參數的反演值.

3 反演算法迭代格式

在求出目標泛函對于控制變量w的梯度之后,本文選擇有限內存擬牛頓優化算法(L-BFGS方法)[18,19],對控制變量w進行迭代,步驟如下：

選擇初始未知參數猜值x0=x0?w0=0,定義d0=-(?J)0=-?wJ(w0);0←k;

1)計算(?J)k+1=?wJ(wk+1);

2)令 sk=wk+1-wk,qk=(?J)k+1-(?J)k;

3)令ρk=1/qTksk,vk=(I-ρkqksTk);

4)計算

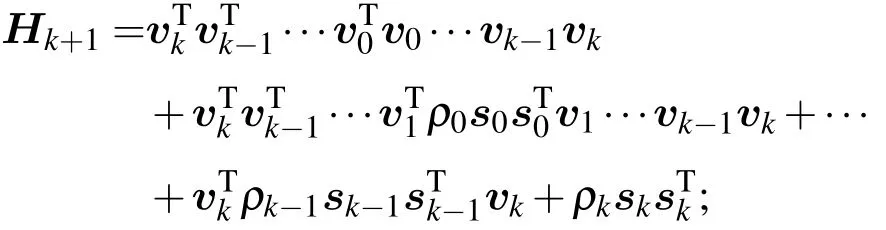
5)令 dk+1=-Hk+1(?J)k+1;

6)更新wk+1=wk+αkdk,湍流系數xk+1=x0+X′wk+1,其中實數αk使得J(xk+1)最小;

返回第1)步,直到迭代收斂為止.

4 兩種計算流程

由(10)式可以看出,在M為線性或非線性非常弱的情況下,MX′在迭代計算過程中變化很小.為了節省計算量,減少集合計算的次數(只需進行一次集合運算),計算流程1如圖1所示.

對于M非線性較強的情況,MX′在迭代計算過程中與x值的變化密切相關,MX′的變化會對反演結果產生較大的影響.為了能準確計算隨x變化的MX′值,計算流程2如圖2所示.

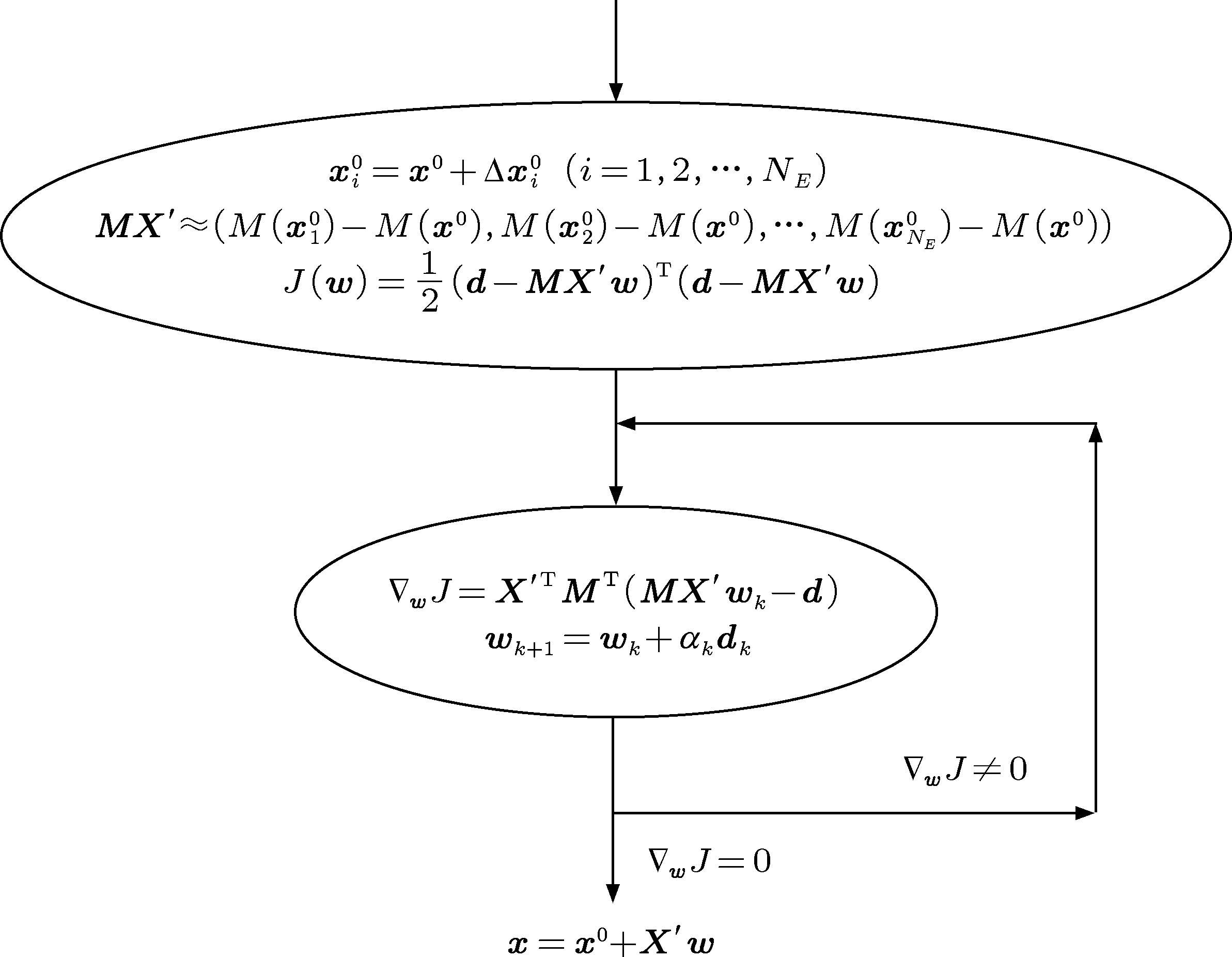
圖1 計算流程1

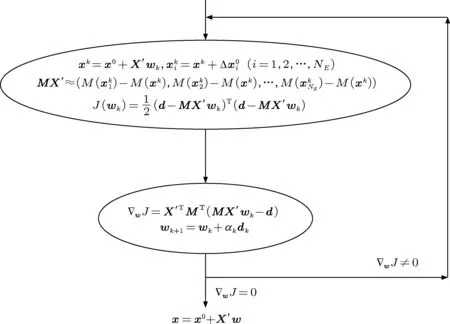
圖2 計算流程2

通過對比分析兩計算流程可以發現,流程2每次求取梯度都需要進行一次集合計算,這無疑使計算量增加了很多.流程2計算量雖然增加了,但在M非線性較強的情況下,可以較為精確地計算MX′值.

5 計算實例

5.1 正演模式

湍流系數k隨時間不變,大氣邊界層定常狀態下的運動方程組為[1]

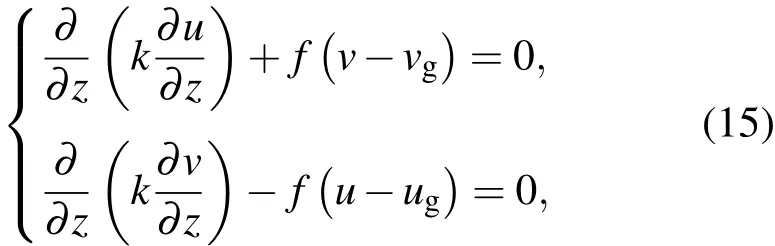
邊界條件為(u,v)|z=0=(0,0);(u,v)|z=H=(uHg,vHg),其中k為湍流系數,u,v為水平風場緯向、經向分量,ug,vg為地轉風緯向、經向分量,f為科氏參數,uHg,vHg為邊界層頂地轉風緯向、經向分量,H為邊界層頂高度.在(15)式中,由湍流系數k計算風場u,v是正演,而根據風場求k就是反演.

在已知探空觀測風場資料uobs,vobs的條件下,可以對湍流系數k進行反演.地轉風場ug,vg可以由水平氣壓分布計算得到,因此在這地轉風作為已知參數.為此,取目標泛函為

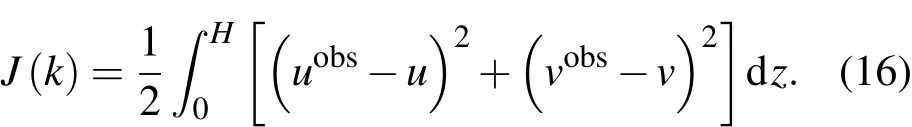
為了進行數值計算,首先對方程(15)進行差分離散,在垂直方向將邊界層平均分為n+1層,即地面為第0高度,邊界層頂為第n+1高度,邊界條件給在這兩個高度上,顯然每層高度為h=H/(n+1).將湍流系數k寫在半格點上,其余量都寫在整格點上,即ki=k[(i-0.5)h],u(i)=u(ih),其余量以此類推,這樣

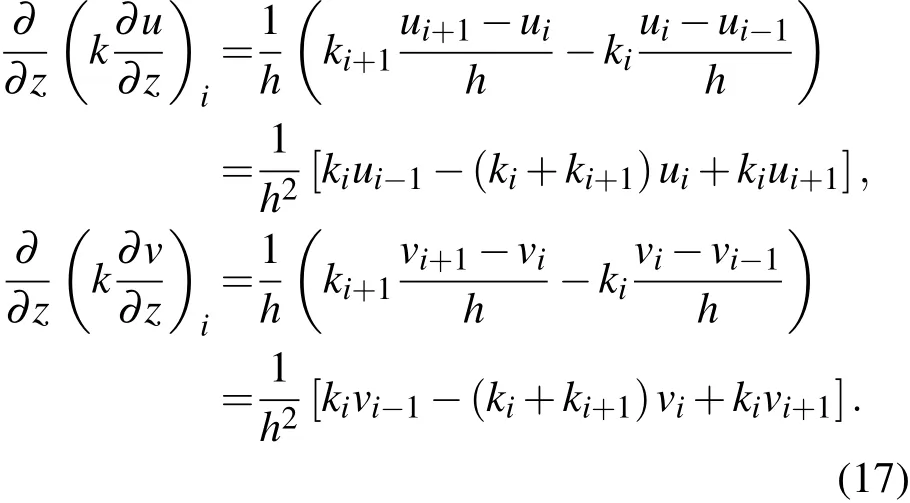
如此代入整理得方程(15)的離散格式.

當 i=2,···,n-1 時,

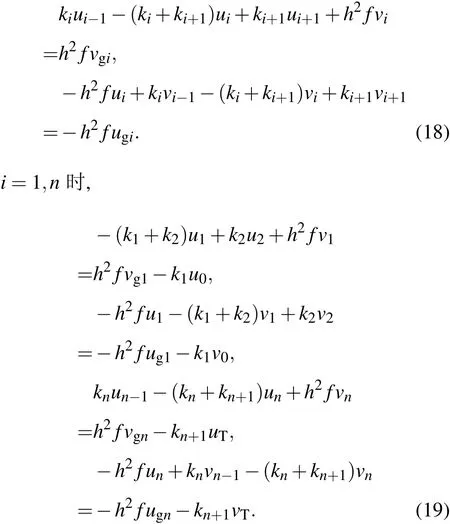
其中uT=uHg,vT=vHg,為邊界層頂地轉風緯向、經向分量.記βi=-(ki+ki+1),n×n階矩陣

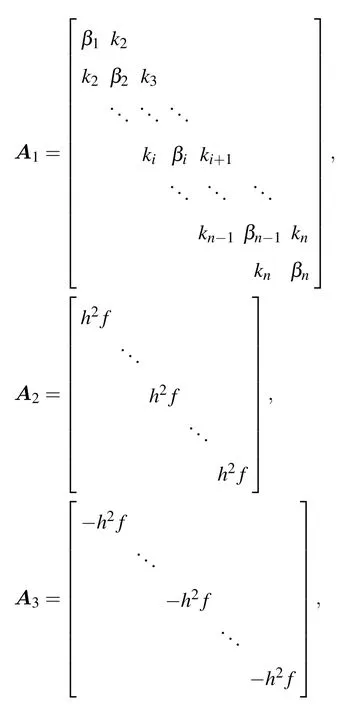
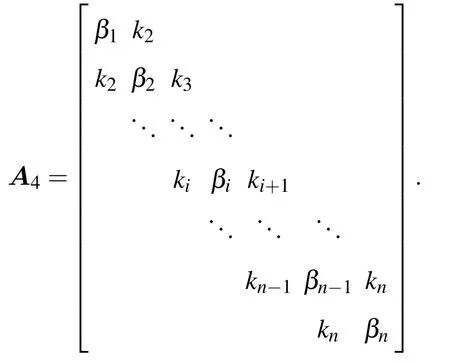
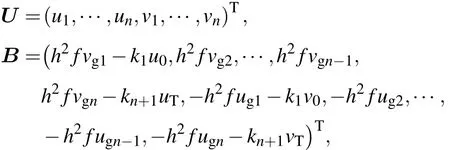
則原正演模式(15)式的離散方程寫成矩陣形式

這樣在給出風速上下邊界值和各系數廓線時,原正問題歸結為解此2n階線性方程組.

目標泛函(16)式是一個垂直方向的定積分,采用梯形公式得

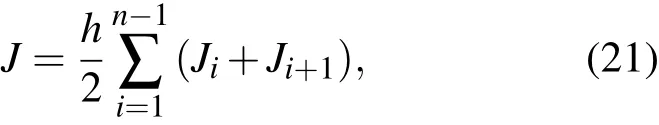
其中

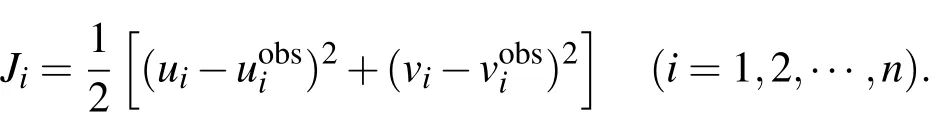
5.2 試驗設計

設邊界層上界高度H=2000 m,取北緯40°的科氏參數f=0.0000937442 s-1,在垂直方向將邊界層平均分為80層.為了對上面的算法進行檢驗,類似于有關文獻選取湍流系數模擬真值(后面都稱其為真值)為如下表達式[20]：

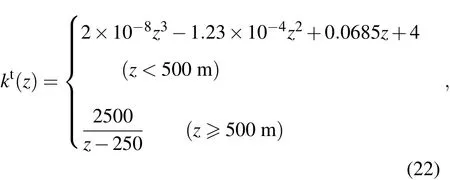
kt(z)的單位為m2·s-1,上標t表示真值.地轉風隨高度線性變化如下：

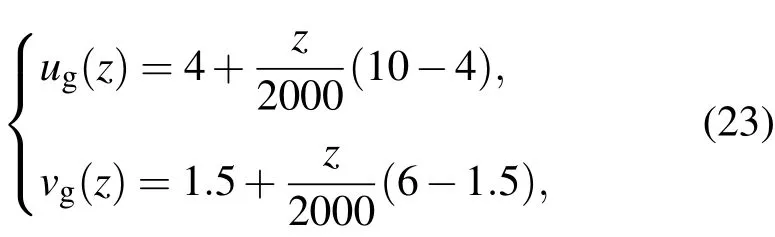
單位為m·s-1.在這些條件下,把正問題求解Ekman方程(20)式得到的u,v作為風場模擬觀測值.根據u,v風場模擬觀測資料,做理想數值試驗.將湍流系數作為未知參量進行反演,與湍流系數真值(即模擬真值)進行對比,來檢驗上述方法的可行性及效果.

為了檢驗初猜值擾動大小及兩種計算流程對反演結果的影響,按初猜值擾動大小設計了兩組試驗：第一組中湍流系數初始猜值擾動較小,初猜值為k(z)=kt(z)+0.1kt(z),集合預報擾動均方差取為0.01 m2·s-1,集合數為100;第二組初始猜值擾動較大,初始猜值為k(z)=8 m2·s-1,集合預報擾動均方差取為0.1 m2·s-1,集合數同樣設為100.同時,在這兩組試驗中分別對兩種試驗流程進行了試驗檢驗.

5.3 試驗結果

圖3給出了第一組數值試驗中湍流系數的真值、初猜值和反演值的結果,其中圖3(a)為流程1的結果,圖3(b)為流程2的結果.在這組試驗中,初始猜值擾動較小,只是真值的十分之一,即初猜值為k(z)=kt(z)+0.1kt(z).從圖3中可以發現,流程2反演結果的精度明顯要高于流程1的結果.對于流程1,湍流系數反演結果在800 m以下精度相對較高,800—2000 m的反演值與真實值相比明顯存在一定幅度的振蕩現象.而對于流程2,可以發現,整個高度上的反演結果都比較接近于真值.

為了更清楚地反映數值試驗結果,圖4給出了第一組試驗中兩個流程的反演值與真值之差.從圖4中可以發現,在整個高度上流程2的反演精度要明顯高于流程1,結論和圖3相同.

圖5給出了第二組數值試驗中湍流系數的真值、初猜值和反演值的結果,其中圖5(a)為流程1的結果,圖5(b)為流程2的結果.在這組試驗中,初始猜值擾動較大,即初猜值為k(z)=8 m2·s-1.從圖5中可以發現,流程2反演結果的精度明顯要高于流程1的結果,這和第一組試驗得到的結論相同.在這組試驗中,對于流程1,湍流系數反演結果與真實值相比在整個高度上都明顯存在一定的震蕩;對于流程2,反演值除了在湍流系數隨高度變化拐角處存在一定誤差外,其他高度上的反演結果都比較接近于真值,反演精度比較高.

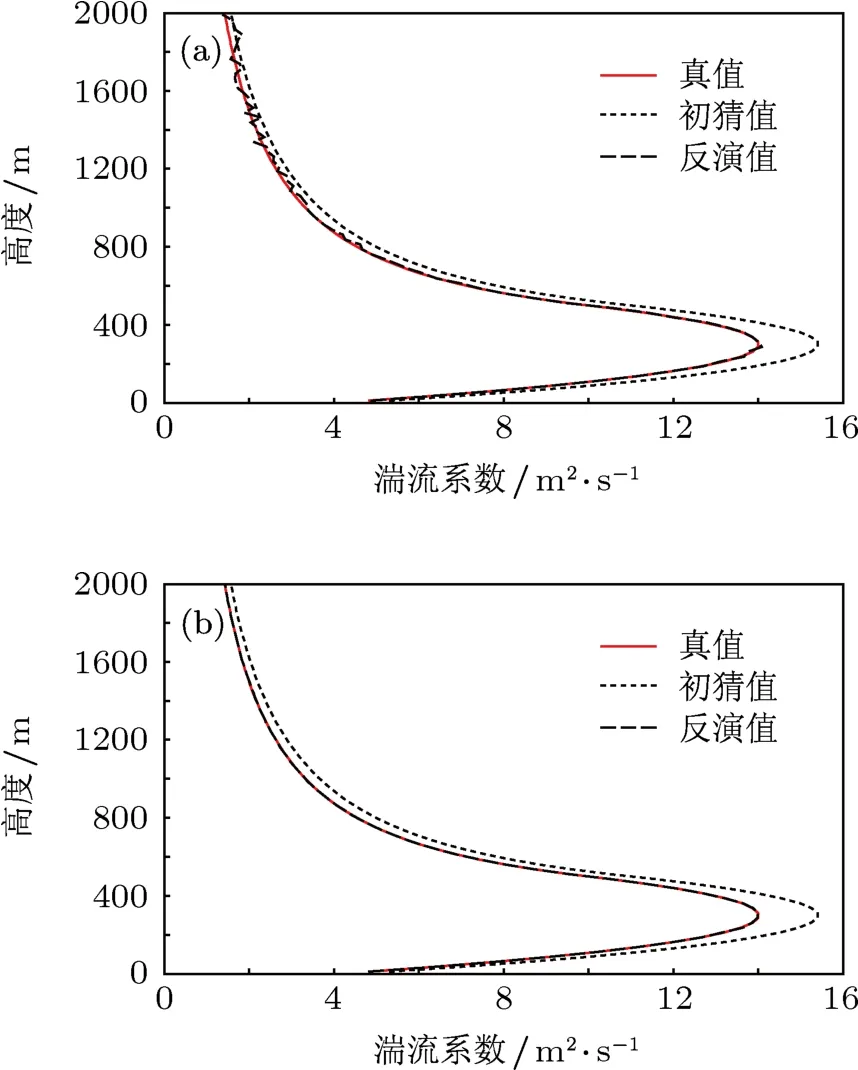
圖3 第一組試驗中湍流系數的真值、初猜值和反演值(a)流程1;(b)流程2

圖4 第一組試驗中反演值與真值之差

圖6 給出了第二組試驗中兩個流程的反演值與真值之差,可以發現,在整個高度上,流程2的反演結果精度要明顯高于流程1,得到的結論與圖5相同.

另外,將圖3、圖4與圖5、圖6相比較,可以發現,除了不同的計算流程對反演結果精度有較大影響外,湍流系數初始值的擾動大小對最后的反演結果也有較大的影響.表1給出了采用集合變分方法反演Ekman層湍流系數兩組試驗中不同計算流程的機器用時(Inter(R)Core(TM)2 Duo CPU T5550,1.83 GHz,1.00 GB的內存)及反演誤差均方差.從表1的數據可以看出,在相同計算流程的情況下,初猜值擾動較小情況下的反演誤差均方差要小于初猜值擾動較大的情況;在初猜值擾動相同的情況下,流程2反演結果的誤差均方差要遠小于流程1,但機器用時要遠高于流程1.

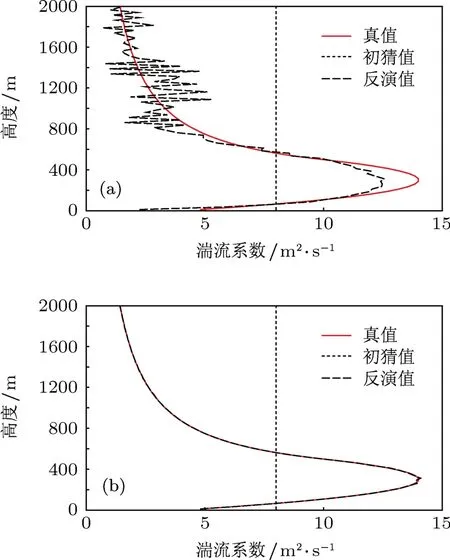
圖5 第二組試驗中湍流系數的真值、初猜值和反演值(a)流程1;(b)流程2

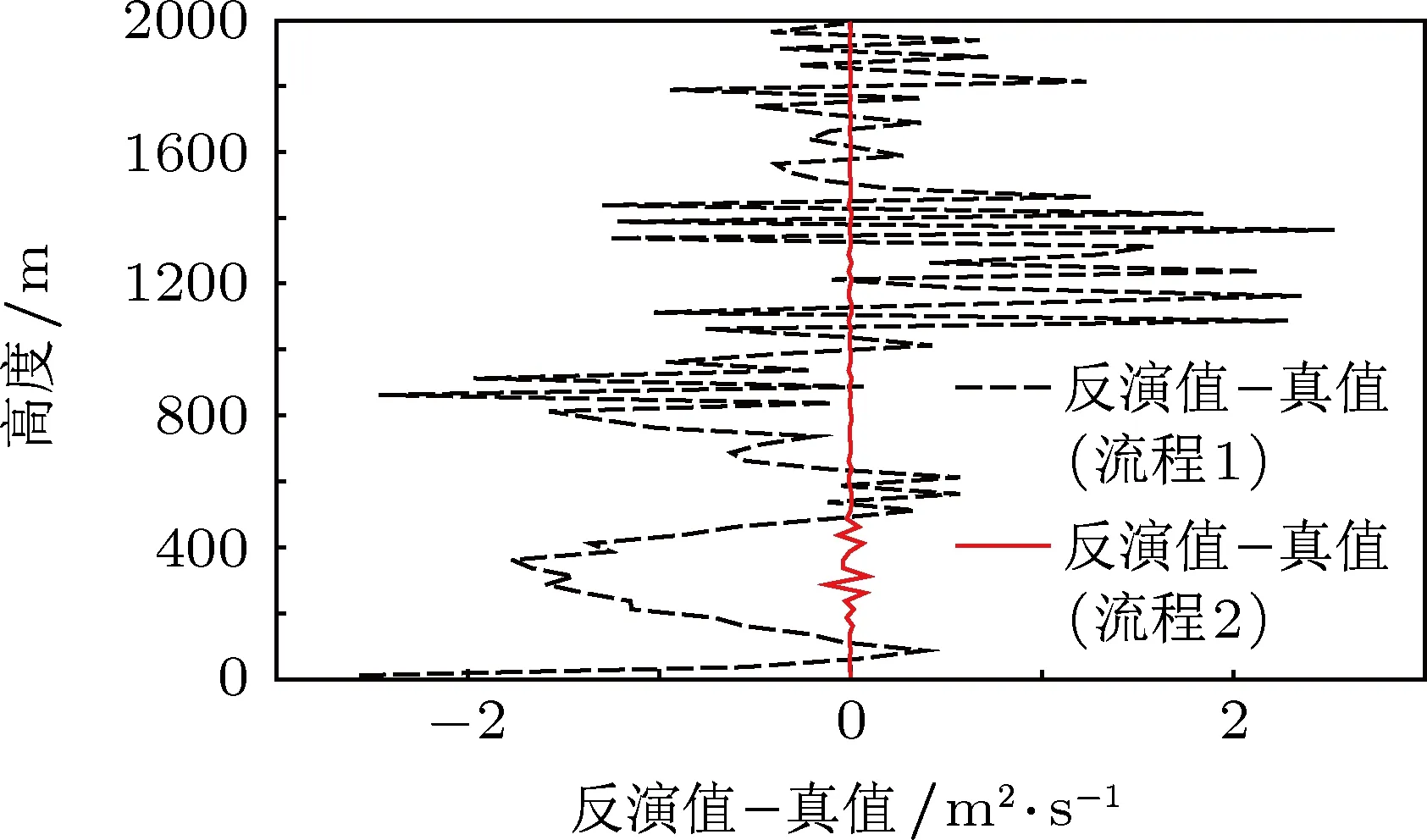
圖6 第二組試驗中反演值與真值之差

綜合以上數值試驗結果可以發現,提出的集合變分梯度計算方案能夠有效減小初猜值中的誤差,使反演值向真實值接近,反演結果的精度與初猜值擾動的大小及反演計算流程有關.

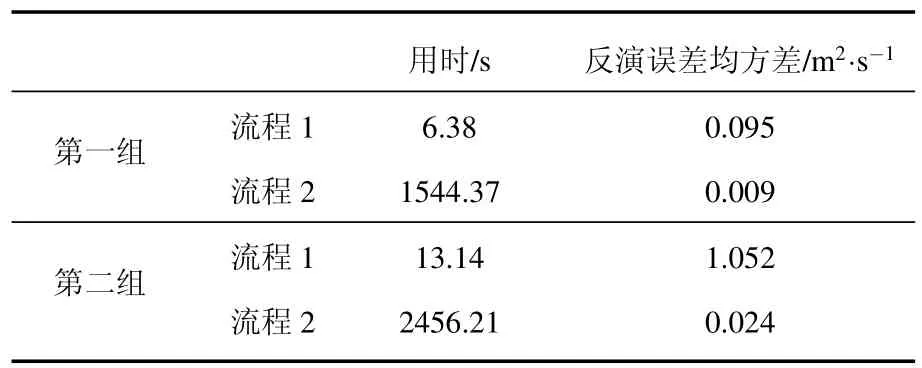
表1 集合變分方法反演Ekman層湍流系數的數值結果

6 結論

在進行大氣邊界Ekman層湍流系數物理反演計算過程中,將集合計算和變分法相結合,提出了目標泛函梯度計算的集合變分方案,避免了根據正演模式推導伴隨模式求梯度的繁瑣過程,此方法的梯度計算只需要正演模式,使得算法實現變得簡單、方便.

采用此方案對大氣邊界Ekman層的湍流系數進行了反演數值試驗.計算結果表明,提出的方案能夠有效減小初猜值中的誤差,使反演值向真實值考近,避免了根據正演模式推導伴隨模式求梯度的繁瑣過程,這說明此反演方法中梯度計算的集合變分方案是可行的.同時試驗結果表明,湍流系數初猜值的擾動大小及不同的計算流程都會對反演結果產生較大的影響.在相同計算流程的情況下,初猜值擾動較小情況下的反演誤差均方差要小于初猜值擾動較大的情況.分析其原因,由反演方法采用的目標函數定義(2)式及集合變分梯度計算方法中集合擾動均方差的選取,此方法實質上是一個極大似然估計方法,因此初猜值擾動小(即誤差小),那么估計值(或反演值)的誤差均方差就小;反之,則反演值誤差均方差就大.另外,在初猜值擾動相同的情況下,考慮MX′隨x變化計算方法(即流程2)的反演誤差均方差要遠小于不考慮隨x變化的反演計算方法(即流程1).這主要是因為,大氣邊界Ekman層模式(即正演模式M)是一個非線性模式,MX′會隨x迭代過程的變化而變化,如不考慮MX′的變化,就會將誤差轉化到最后的反演結果上,從而產生較大的反演誤差.

[1]Berger B W,Grisogono B 1998 Bound.Layer Meteorol.87 363

[2]Masson V 2000 Bound.Layer Meteorol.94 357

[3]Grimmond C S B,Oke T R 2002 J.Appl.Meteorol.41 792

[4]Chen J,Kemna A,Hubbard S S 2008 Geophysics 73 247

[5]Sheng Z,Huang S X 2010 Acta Phys.Sin.59 1734(in Chinese)[盛崢,黃思訓2010物理學報59 1734]

[6]Zhang Y,Yang X,Gou M J,Shi Q F 2010 Acta Phys.Sin.59 3905(in Chinese)[張宇,楊曦,茍銘江,史慶藩2010物理學報59 3905]

[7]Ye H X,Jin Y Q 2009 Acta Phys.Sin.58 4579(in Chinese)[葉紅霞,金亞秋2009物理學報58 4579]

[8]Zhang Y Q,Ge D B 2009 Acta Phys.Sin.58 4573(in Chinese)[張玉強,葛德彪2009物理學報58 4573]

[9]Zuo H Y,Yang J G 2007 Acta Phys.Sin.56 6132(in Chinese)[左浩毅,楊經國2007物理學報56 6132]

[10]Wei B,Ge D B,Wang F 2008 Acta Phys.Sin.57 6290(in Chinese)[魏冰,葛德彪,王飛2008物理學報57 6290]

[11]Huang C J,Liu Y F,Wu Z S,Sun Y Q,Long S M 2009 Acta Phys.Sin.58 2397(in Chinese)[黃朝軍,劉亞峰,吳振森,孫彥清,龍姝明2009物理學報58 2397]

[12]Hao N,Zhou B,Chen L M 2006 Acta Phys.Sin.55 1529(in Chinese)[郝楠,周斌,陳立民2006物理學報55 1529]

[13]Shi X M,Xiao M,Fan J K 2009 J.Geophys.52 1140(in Chinese)[師學明,肖敏,范建柯2009地球物理學報52 1140]

[14]Wang J Y 2007 J.Engin.Geophys.4 1(in Chinese)[王家映2007工程地球物理學報4 1]

[15]Kelbert A,Egbert G D,Schultz A 2008 Geophys.J.Inter.173 365

[16]Cohn S E 1997 J.Meteor.Soc.Japan 75 257

[17]Jazwinski A H 1970 Stochastic Processes and Filtering Theory(1st Ed.)(New York：Academic Press)p376

[18]Liu D C,Nocedal J 1989 Math.Programming 45 503

[19]Nocedal J 1980 Math.Comput.35 773

[20]Zhao M 1987 Adv.Atmos.Sci.4 233