利用小波神經網絡對單相三電平逆變器諧波檢測

馬 輝，王玉華，劉朋朋

（長春工業大學，吉林長春 130000）

1 引言

隨著電力電子技術的發展，各種變頻器、變流器、開關電源和電抗器等非線性設備在電力系統中應用的增多，這些器件在對電網進行整流、逆變時會產生大量的諧波[1-2]。諧波檢測是治理諧波的一個重要環節，快、準、實時的諧波檢測是國內外學者致力研究的目標，檢測方法盡不相同。

小波變換在時域和頻域同時具有良好的局部化性質;神經網絡具有自學習、自適應、魯棒性、容錯性和推廣能力[3-5]，把小波變換與神經網絡有機的結合起來，充分利用兩者的優點。小波神經網絡最早是由法國著名的信息科學機構IRLSA的Zhang Qinghu等人1992年提出來的［6］,小波神經網絡（Wavelet Neural Network，WNN）是基于小波變換構成的神經網絡模型，即用非線性小波取代通常的神經元非線性激勵函數。本文運用非線性小波基取代多層神經網絡的神經元非線性激勵函數，非線性小波變換具有時頻局部特性和變焦特性[7-8]，使得多層前饋神經網絡和小波變換有效互補性的結合起來，達到精確、快速、實時諧波檢測的目的。在matlab/Simulink環境下進行仿真，驗證該方法的精確性、快速性、實時性。

2 小波神經網絡模型

傳統神經網絡隱含層的傳輸函數為非線性函數，輸出層為線性函數，小波變換的時頻聚焦性和平移伸縮特性引入神經網的算法，由小波變換的定義可知，小波變換是利用一個大小可調的窗口函數對要分析的諧波信號進行卷積，再通過調節窗口的大小和位置，將諧波信號的局部結構映射到時頻平面上。小波基函數替代傳統神經網絡的隱含層非線性傳輸函數，并利用小波變換逐層分解的特性對信號進行分析，構成WNN，結構如圖1所示。

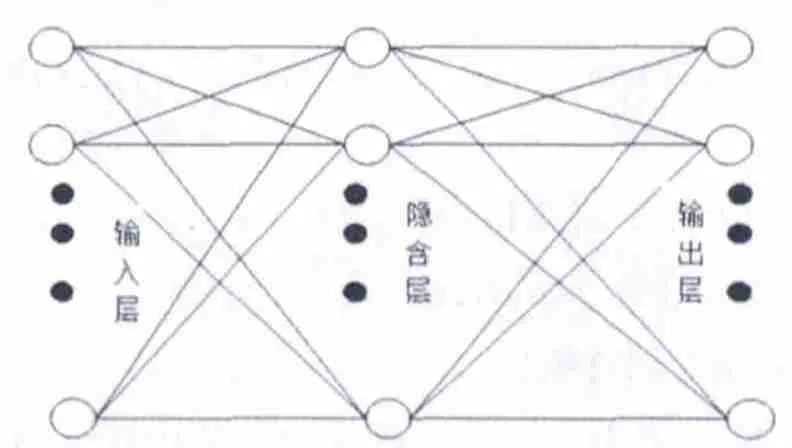
圖1 小波神經網絡的基本模型

本文所述的WNN為三層網絡，輸入層到隱含層的神經元采用全連接，它們的權值和閾值分別對應著小波的伸縮和平移參數，這兩個參數可以通過對訓練數據進行時頻分析后獲得。隱含層到輸出層的權值參數通過線性優化的方法獲得。

基于這種構思所構成的小波神經網絡如圖1所示，其輸出表達式為：

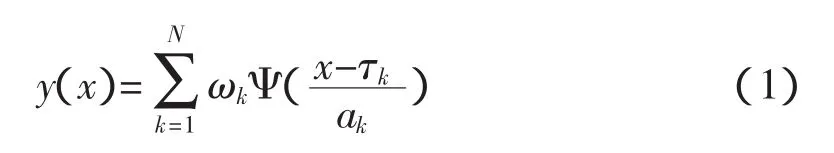
其中：ωk是隱含層第k個節點到輸出層的權值；τk是第k個隱含層節點的閥值，即小波函數的平移參數；ak是輸入層到第k個隱含層節點的權值，即小波函數的伸縮參數；N表示隱含層的節點數。

3 小波基函數的選擇

Harr小波在t∈［0，1）的單個矩形波，即

與之對應的尺度函數為：

經過二進伸縮和平移得：

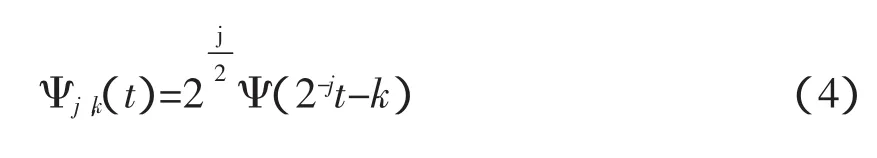
式（4）可以構成線性平方可積空間L2（R）的標準正交小波函數基。從以上分析得出Harr小波計算簡單，另外還有具有獨特的優點：

Harr小波所具有的獨特優點是它可以在2j的多分辨率上構成一組最簡單的正交歸一的小波組。

4 Harr網絡參數的確定

4.1 權值和閥值的初始值選擇

每個隱含層節點對應的小波基函數的窗口寬度和通過隱含層節點來劃分的小區間長度應該一致。但是為了小波基函數能夠在各個區間進行疊加，各個窗口寬度應該乘以一個小系數，使各個小波基函數的窗口稍大于小區間的長度。本文所述WNN按照此思路來取網絡的權值a和閥值τ，設M個輸入，每段小區間的上限和下限為每個隱含層節點的上限和下限，設xjmax為輸入層第j個神經元的輸入樣本，xjmin為最小。

其中：Δx0為小波母函數的窗口寬度，x0為窗口中心。

4.2 輸入層和隱含層節點的確定

對本文的多維輸入WNN中，輸入層神經元的個數來自于待測信號的取樣點個數，考慮奈奎斯特采樣定理和分析信號的最高次諧波頻率，在一個基波周期內最高次諧波出現的次數為最低采樣點的一半，由此來確定輸入節點的個數。

隱含層節點的數據是通過隱含層的小波基函數的卷積運算而得，在離散的情況下卷積運算空間應滿足覆蓋整個傳輸函數的取值空間。

任意一個隱含層神經元的輸出函數為：

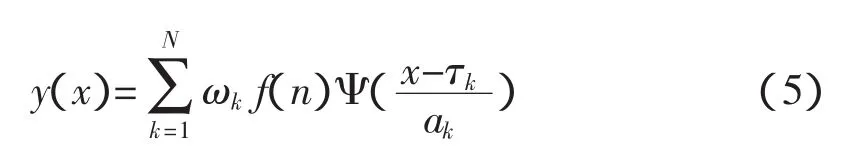
式中：f（n）為輸入函數；ωk為連接隱含層神經元和輸入層的權；N為輸入層結點個數。由式（5）卷積運算的取值空間覆蓋整個小波基函數的取值空間，由此來確定隱含層神經元個數。

5 時變諧波檢測的算法

5.1 算法理論推導

任意實際信號f（t）在一定時間范圍的Harr小波展開可表示為：

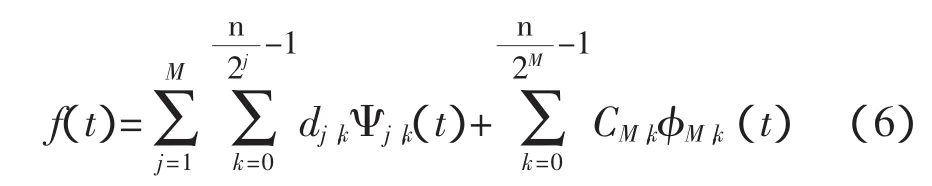
式中：n為對f（t）的采樣點數，此處取2的整次冪；M為對f（t）進行小波變換的尺度數；dj，k為f（t）在第j個尺度的細節函數；CM，k為f（t）在第M個尺度上的逼近系數。

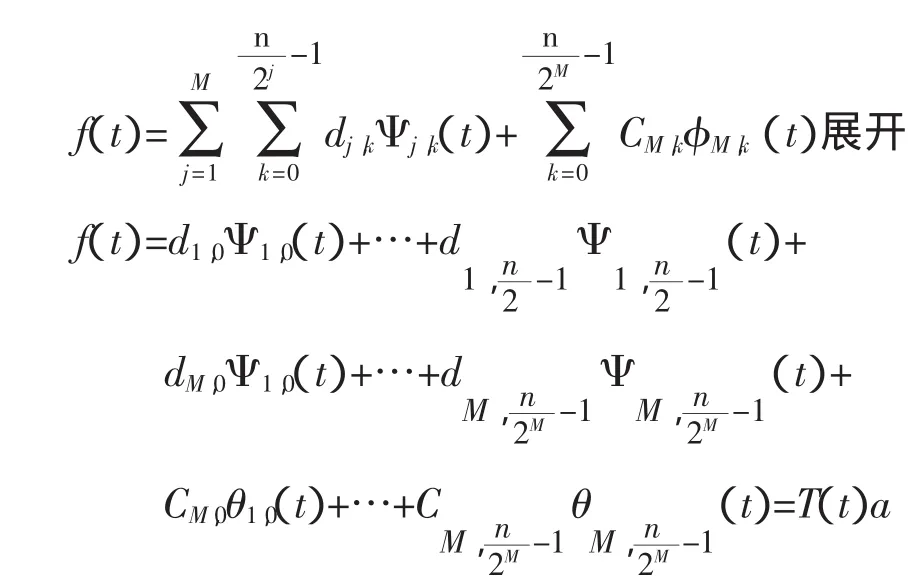
式中T（t）和a分為：

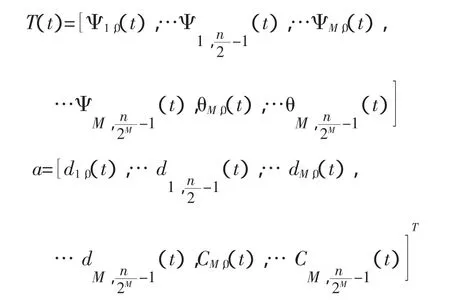
對上述函數取n個離散值，可得到一組序列：

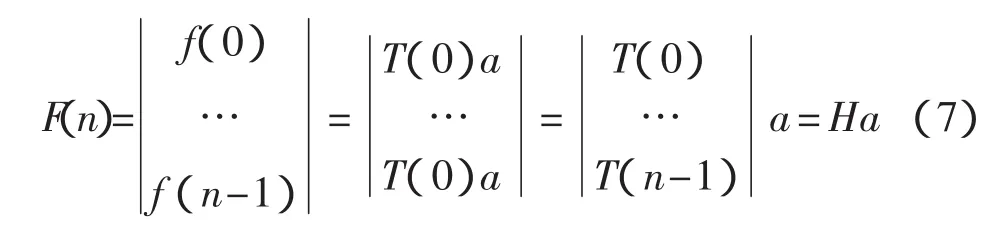
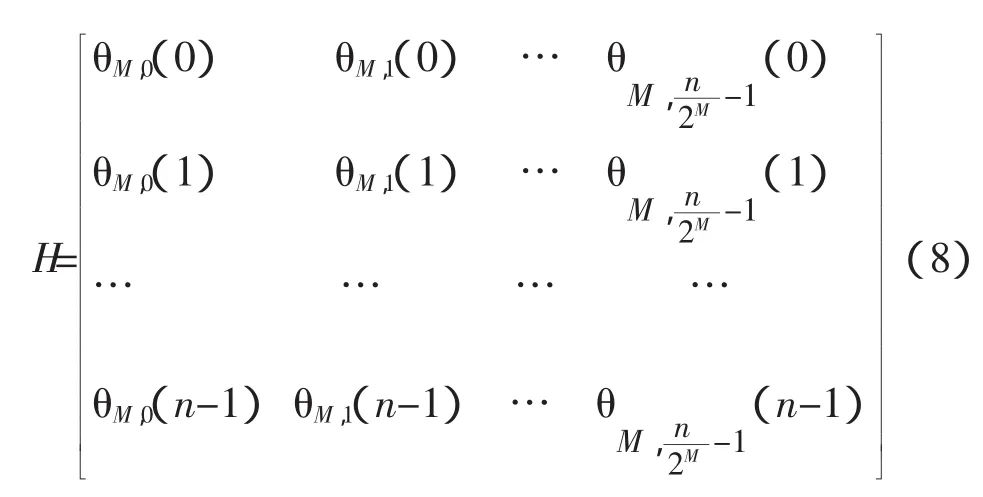
本文稱H為小波變換矩陣，H是n維方陣，且H、n、分解尺度和選擇小波函數有關。

5.2 網絡的訓練模式

本文為網絡為3層，網絡的性能指標采用均方差誤差（liner means square，LMS），其表達式：

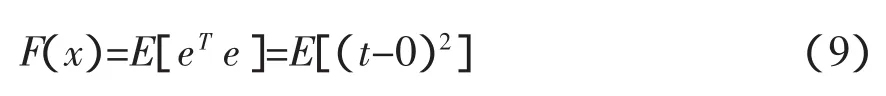
F（x）為網絡性能指數函數，t為目標輸出向量，0為實際輸出向量。但是在實際應用中，為運算方便采用近似LMS公式，即為：

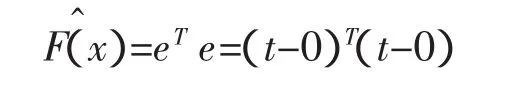
網絡參數的自動更新必須利用神經網絡的敏感反向傳播，不同的網絡模型、不同隱含層傳輸函數決定傳播時的不同方程。針對本文的網絡，需要確定輸入層對隱含層敏感傳播系數和隱含層對輸出層的敏感傳播系數

由于輸出層的傳輸函數為線性函數，則輸出層的傳輸函數求關于輸入的偏導數，即可得到輸出層傳播敏感系數＝1。分別對式（1）中的網絡權值ωk、平移參數τk和伸縮參數ak求偏導，得到均方差誤差函數對于不同參數的梯度，即隱含層對于不同參數的反向傳播敏感系數，求偏導數分別為：

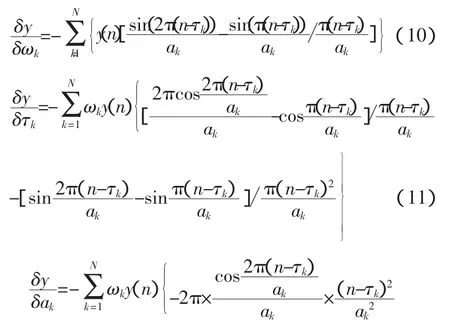
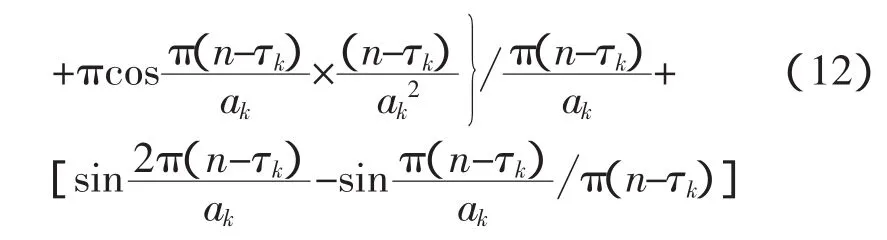
由網絡性能指數來計算敏感度的傳播公式：

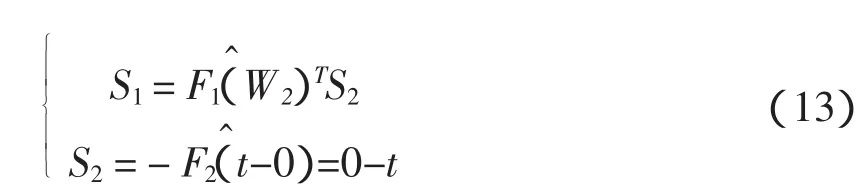
式中：S1，S2分別為隱含層和輸出層的反向傳播函數敏感度為反傳系數，W2為（10）—（12）的各項反向傳播敏感度的各項偏導數。

6 仿真實驗

6.1 Matlab/Simulink模型

本文以單相三電平的逆變電路作為諧波源的仿真模型。通過Matlab/Simulink設計簡單的單相橋式逆變電路。如圖2所示是電壓型全橋逆變模型。

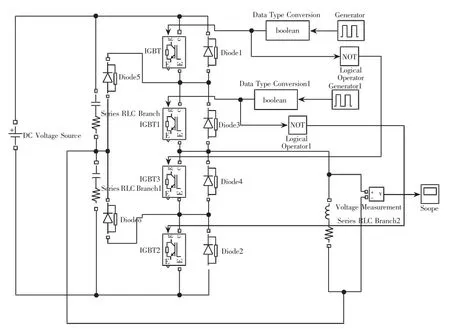
圖2 負載電壓發生模型

在理想情況下，逆變裝置的切換將使輸入逆變裝置交流側的波形發生畸變，電力系統中實際產生的諧波多為2n+1次，一般各奇次諧波的幅值不會超過基波幅值的50%，且諧波次數越高幅值就越小[10]。時變諧波信號如下：

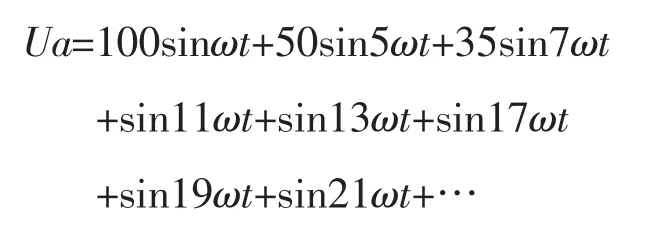
諧波次數達到19次以后，諧波對應的幅值已經不到基波的1/20。將信號的基波和五次到十九次諧波作為研究對象。

6.2 仿真結果分析

諧波信號為時變信號，在確定訓練樣本時，采樣周期進行等時位移，采樣點數在每一周期T內大于40，這樣對所有時變諧波都能作為訓練樣本。接下來采用5.2節所述的方法對網絡進行訓練，網絡經過128次的訓練實現了收斂，則諧波頻譜為：

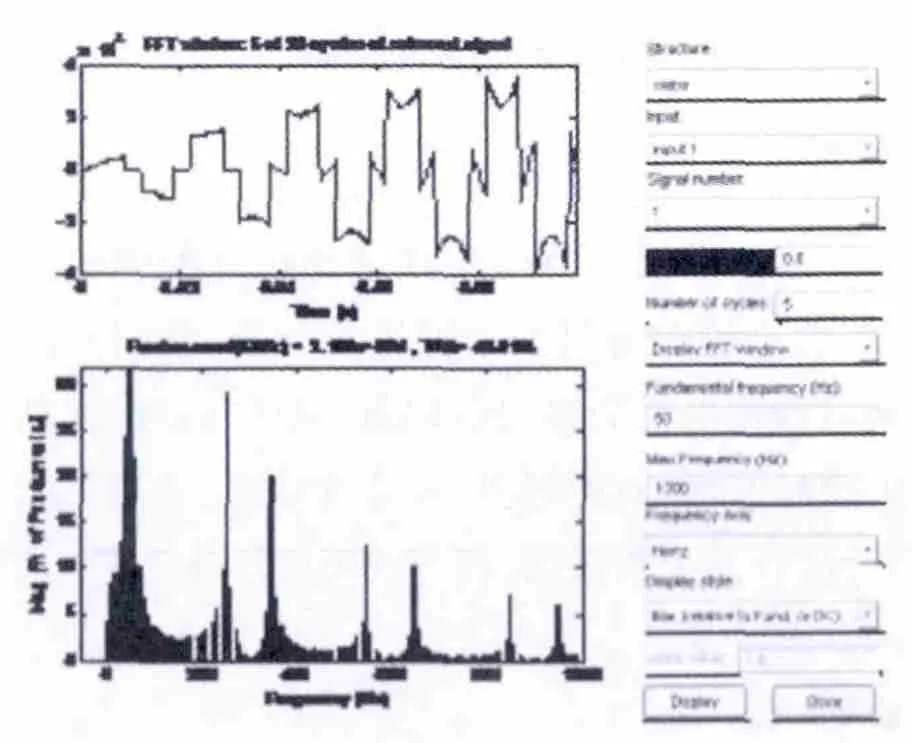
圖3 利用WNN對A相時變諧波電壓信號進行檢測的結果

有網絡神經本身具備自主學習功能，經過經神經網絡的處理，同時引入小波分析的頻率局部化功能，通過對時頻自適應窗口進行濾波，使得WNN對于非平穩信號同樣具有的精度[11]。

通過傳輸函數的小波分析，借助小波變換的時頻分析特性和對隱含層小波傳輸函數系數進行分析，可得出幅值在時域上的變化。圖4所示是基波在時域和幅值上在給定和估計值通過WNN檢測,圖5所示是諧波信號用小波檢測和WNN檢測結果的比對，通過分析可以看出小波神經網絡檢測諧波信號精確。

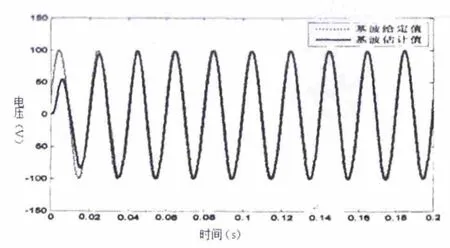
圖4 基波檢測結果

圖5 諧波檢測結果

7 結論

本文采用的算法精確度比傳統的神經網絡高，能準確的對時變諧波進行分析，利用小波變換對諧波信號的幅值和相角很好的逼近，在結合上神經網絡的自學特性和訓練模式，改善了網絡特性。仿真分析表明，該方法可用作諧波信號的檢測有效手段。

［1］王兆安，楊君，劉進軍.諧波抑制和無功功率補償［M］.北京：機械工業出版社，1998.

［2］Georg J W.Power System Harmonics-Fundaments，analysis and filterdesign［M］.Berlin：Spring Press，2001.

［3］袁曾任.人工神經網絡及其應用［M］.清華大學出版社，1999.

［4］危韌勇，李志勇.基于人工神經元網絡的電力系統諧波測量方法［J］.電網技術，1999，23（12）：20-23.

［5］湯勝清，程曉華.一種基于多層向前神經網絡的諧波檢測方法.中國電機工程學報，2006，26（18）：90-93.

［6］Zhang Qinghua.Albert Benvensite Wavelet Networks 1992.

［7］杜天軍，陳 光，雷 勇.基于混疊補償小變換的電力系統諧波檢測方法［J］.中國電機工程學報，2005，25（3）：36-45.

［8］王建頤，冉啟文，紀延超等.基于小波變換的時變諧波檢測［J］.電力系統自動化，1998，22（8）：19-24.

［9］Martin T H，Howard B D，Mark H B.Neural network design［M］.MunichGermany：Thomson Learning Press，1996.

［10］林湘寧，程世杰等.小波分析基礎理論及其電力系統中的應用［J］.電力系統自動化，1997，21（11）：75-80.

［11］SANTOSO S． Power quality assessment via wavelet transform analysis．IEEET ransonpower Delivery，1996，11（2）：924-932．