蜻蜓翼三維流動結構的演變

賴國俊 申功炘

（北京航空航天大學 航空科學與工程學院，北京 100191）

蜻蜓前翼與后翼的距離很近，前后翼之間存在復雜的流動干擾現象.文獻［1］較早地研究了蜻蜓Aeschna juncea，發現蜻蜓翼的升力形成機制與非定常效應有關.文獻［2］的實驗研究表明：前翼的氣動力幾乎保持不變，不受拍動模式變化的影響；當后翼領先前翼大約0.25T拍動時，后翼的氣動力才能恢復到不存在前翼尾跡干擾的水平.文獻［3－4］的數值模擬結果顯示蜻蜓懸停飛行時前后翼之間的流動干擾會削弱總升力（vertical force）.文獻［5］的數值模擬研究結果表明：在懸停拍動模式下，前后翼在下拍時都產生了前緣渦；當蜻蜓翼位于上拍的中間位置時（此時上拍迎角為8°），后翼上翼面為附著流動，并不存在前緣渦.文獻［6］的研究指出當后翼位于前翼的尾跡區時前翼尾跡的下洗效應會減小后翼的有效拍動迎角.文獻［7］的測力實驗顯示：在同相拍動、后翼領先0.25T拍動和反相拍動等3種拍動模式下前后翼的時均升力系數都比單翼的時均升力系數小.

拍動翼的升力機制與拍動翼周圍的三維流動結構有密切聯系［8－11］.由于前后翼流動干擾的存在，蜻蜓翼的升力形成機制變得更為復雜.前后翼流動干擾會對蜻蜓翼周圍的三維流動結構產生影響，進而使蜻蜓翼的升力發生變化.前人文獻中鮮有研究蜻蜓翼周圍的三維流動結構.本文對單個蜻蜓翼周圍的三維流場進行了實驗研究，為以后進一步探索蜻蜓前后翼流動干擾對蜻蜓翼升力的影響奠定基礎.

本實驗利用機電運動模擬機構模擬了一個蜻蜓翼的拍動，使用數字體視粒子圖像測速技術（DSPIV，Digital Stereo Particle Image Velocimetry）和多切面鎖相技術分別測量了兩個下拍拍動相位時刻（t＝0.25T，0.375T）和兩個上拍拍動相位時刻（t＝0.75T，0.875T）蜻蜓翼周圍的瞬時空間三維流場，并對重要的三維流動結構進行了重構和定量分析.

1 實驗方法

1.1 蜻蜓翼形態學參數和運動學參數

實驗參考了蜻蜓Aeschna juncea的相關形態學參數和運動學參數［1，12］.蜻蜓 Aeschna juncea前后翼的平均展長為47.4mm和46mm，平均弦長為8.1mm和11.2mm，平均展弦比為5.85和4.11.實驗選用平面形狀簡化的剛性模型翼來近似模擬真實的蜻蜓翼（見圖1）.模型翼的展弦比為5，展長L＝150mm，厚為1mm.模型翼的展弦比與蜻蜓 Aeschna juncea的展弦比相近［1，13］.實驗證明［14］這種簡化模型翼能夠模擬真實蜻蜓翼周圍的主要流動結構，對平面形狀的簡化處理是合理的.

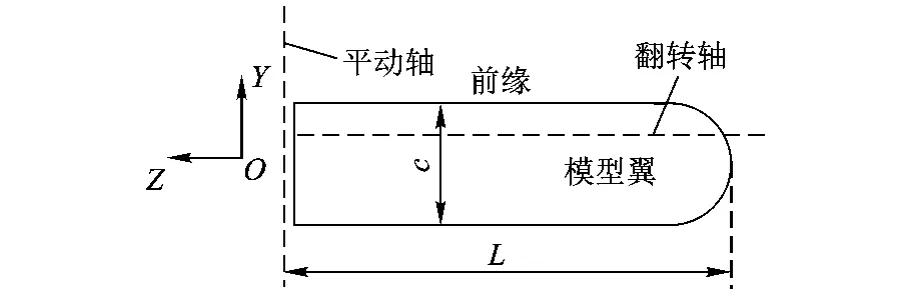
圖1 模型翼示意圖

蜻蜓翼的拍動為3自由度的定點轉動，可分解為：平動（translation），翻轉（rotation）和拍動平面偏移（deviation of stroke plane）.文獻［15－16］的研究表明，蜻蜓翼展弦比相對較大，蜻蜓翼拍動中拍動平面偏移對升力貢獻不大.故本實驗所使用的運動模擬機構只模擬平動和翻轉，不模擬拍動平面的偏移運動.本文把拍動翼由拍動的上極限位置向下極限位置的運動稱為下拍（downstroke），把拍動翼由拍動的下極限位置向上極限位置的運動稱為上拍（upstroke），見圖2.平動運動是指整個拍動翼在其拍動面內繞翼根所作的往復定軸轉動.蜻蜓在懸停和自由前飛時，其拍動翼的平動速度隨時間變化近似為正弦函數［17］.平動的運動函數為

其中，Φ＝π／3為拍動幅角；T＝5s為拍動周期；γ＝0為初始相位.翻轉運動是指拍動翼在其拍動的極限位置附近繞其翻轉軸作定軸轉動，見圖1和圖2.翻轉軸大約在距拍動翼前緣0.25c（c為拍動翼弦長）處［18］.前后翼翻轉軸之間的距離為1.25c.翻轉的運動函數為分段函數：

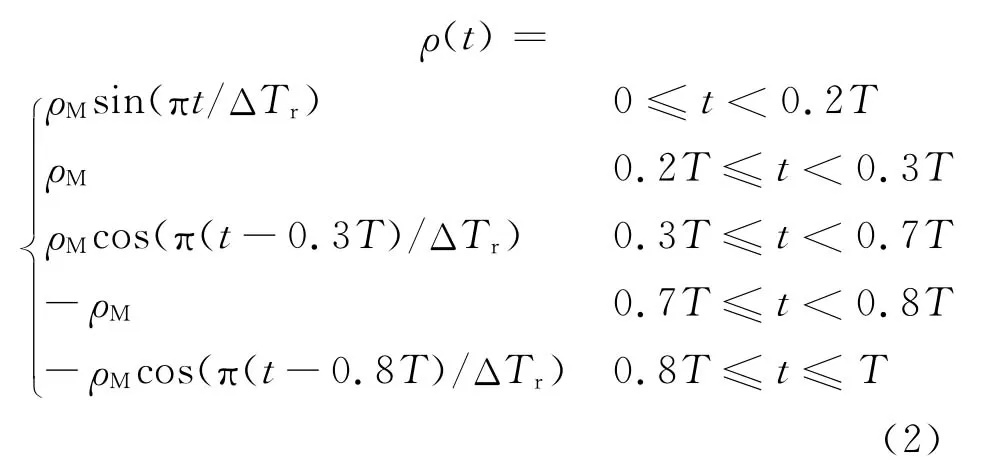
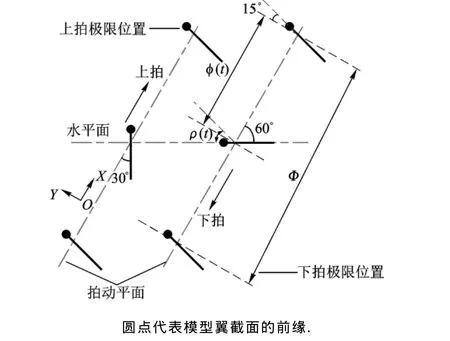
圖2 模型翼運動示意圖

其中，ΔTr＝0.4T為翻轉持續時間；ρM＝π／4為翻轉幅角.平動運動的函數曲線和翻轉運動的函數曲線見圖3.在t＝0時，模型翼位于拍動的上極限位置.

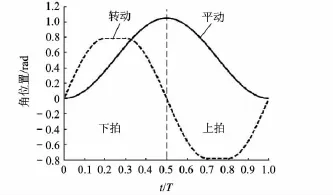
圖3 平動運動和翻轉運動的函數曲線

實驗測量了4個拍動相位：0.25T，0.375T，0.75T，0.875T.其中，0.25T和0.75T分別為下拍和上拍的中間時刻，此時的平動速度最大，但兩個時刻的平動速度方向相反.0.375T和0.875T都是拍動翼從拍動中間位置到極限位置拍動的中間時刻.此時，平動速度正在下降，但翻轉速度在上升，拍動翼的迎角在持續增大.

本文雷諾數的定義為

其中，Φ＝π／3，為拍動幅角；n＝0.2Hz，為拍動頻率；c＝30mm，為平均弦長；v＝1.01×10－6，為水的運動粘度系數；r2為特征半徑，取拍動翼面積的二次矩半徑，定義如下：

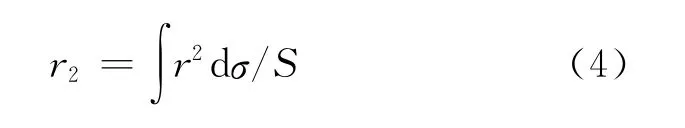
其中S為拍動翼的面積.本模型翼的特征半徑r2＝84.8mm.因此，本實驗的雷諾數Re＝1 011，與蜻蜓Aeschna juncea在懸停飛行狀態下的雷諾數1 380［1，3］相近.

1.2 DSPIV實驗布局和數據處理

本實驗在一個透明水槽中進行.水槽的尺寸為1m×1m×0.9m.DSPIV的實驗布局如圖4所示，一臺Nd：Yag固體脈沖激光器被放置在水缸右側的光學平臺上，作為DSPIV照明光源.激光在經過一個片光光路后變成片光.在觀測區域，片光厚度約為3mm.兩個連續激光脈沖的間隔由測量拍動相位流場的平均速度決定.在實驗中，兩個連續激光脈沖的時間間隔根據所測量的拍動相位設為8～10ms.實驗使用空心玻璃珠作為示蹤粒子.空心玻璃珠的直徑為1～5μm，與水的比重為1.05.

在DSPIV測量中，兩臺數字相機采用非對稱的角位移布局（見圖4）.一臺相機1被安裝在正對觀測區域的位置；另一臺相機2的安裝角度與觀測平面的法線方向約成40°.斜置相機2被安裝在一個角度調節器上，以調節相機鏡頭平面與相機芯片平面之間的夾角，滿足Scheimpflug成像條件（見圖4）.相機到觀測平面的距離約為130cm.兩臺相機的共同視場大小約為7.0cm×14.1cm.

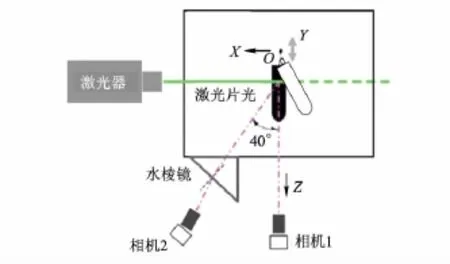
圖4 DSPIV實驗布局示意圖

本實驗采用透明膠片紙作為校正／標定板.校正和標定的計算均由同一個自編的Matlab程序完成.幾何校正計算使用了基于雙調和樣條函數的多次幾何校正算法［19］.本實驗使用立方天地公司的商業軟件MicroVec?對校正后的粒子圖進行互相關計算.每幅粒子圖看得到一個126×62面內速度矢量場.

拍動翼周圍的流場呈周期性，主要流動結構出現的頻率與拍動翼拍動的頻率一致.為獲得拍動翼周圍的三維流動結構，本實驗采用了“鎖相”技術.本實驗在每個拍動相位下分別測量了拍動翼從翼根到翼梢的17個截面流場（截面位置的間距為10mm，有2個在翼梢之外，見圖5a）.所以，在每個測量拍動相位下所得到的三維速度場共有126×62×17個速度矢量.本實驗采用“相位平均”來減小實驗測量數據的隨機誤差.在同一個拍動相位下，每個截面位置的流場均連續測量35個周期，然后取后30個流場進行平均，作為本實驗的測量結果.舍掉前5個周期的測量結果是為了消除初始流場的非定常流動現象的負面影響.“相位平均”處理前后的空間速度矢量場對比見圖5.

本文選用λci準則進行渦的識別.漩渦強度λci是當地速度梯度張量的特征方程的復特征根的虛部，描述了當地流體微團的“旋轉強度”［20］.λci值越高表明當地流體微團旋轉得越快.本實驗使用閾值等值面4.2來繪制λci的等值面，以顯示拍動翼周圍的渦結構，如圖6所示.本實驗還使用｜ωz｜的截面等值線顯示渦結構，如圖7所示.

圖5 相位平均處理前后的速度矢量場

圖6 拍動翼渦結構的λci等值面

本實驗把拍動翼前緣渦在各個截面的λci局部極值點定為前緣渦渦核在該截面的位置.對前緣渦渦核線距離翼面的垂直高度h進行了計算，并繪制了渦核高度h與截面位置z關系的曲線圖.對前緣渦的截面環量Γz也進行了計算.根據Burgers漩渦模型，前緣渦的邊界由當地渦量｜ωz｜極值的1／e來確定［21－22］.同時，也繪制了截面環量Γz與截面位置z關系的曲線圖.

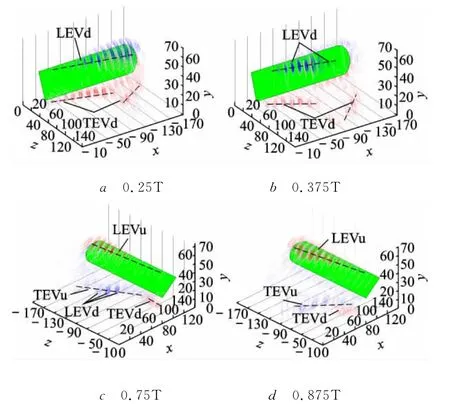
圖7 拍動翼渦結構的ωz等值線

2 實驗觀測結果及討論

2.1 0.25T時刻的拍動翼流場

如圖6a所示，下拍前緣渦（LEVd，Leading Edge Vortex in the downstroking）從前緣z＝0.13L處開始形成.從λci等值面沿展向（負z方向）不斷膨脹可知，LEVd的漩渦強度沿展向不斷增強.｜ωz｜等值線圖（圖7a）顯示，LEVd的空間結構呈錐狀，而且有點扁.如圖8a所示，從翼根至翼梢，LEVd的渦核線逐漸遠離前緣，并逐漸遠離翼面（從z＝0.67L到翼梢）.如圖9a所示，LEVd的截面環量Γz沿展向升高，在z＝0.87L處達到Γz，max后略微下降.

翼梢渦（WTV，Wing Tip Vortex）在翼梢卷起，并與LEVd和下拍后緣渦（TEVd，Trailing Edge Vortex in the downstroking）相連.從后緣脫落下來的TEVd與后緣的距離從翼根到翼梢越來越大（見圖6a）.如圖7a所示，TEVd也成錐狀，它的｜ωz｜從z＝0.67L開始突然變弱；在外翼段（從z＝0.8L到翼梢），有新的TEVd開始從后緣脫落.

2.2 0.375T時刻的拍動翼流場

LEVd從翼根開始形成，見圖6b.λci等值面顯示：它的長度比0.25T時刻更長；它的漩渦強度也比0.25T時刻更強.｜ωz｜等值線圖（圖7b）顯示，在各個截面里，0.375T時刻LEVd比0.25T時刻更強；從z＝0.8L到翼梢，LEVd的渦量集中區越來越大，且變得松散，部分渦量開始從LEVd上脫落.如圖8b所示，LEVd渦核線比0.25T時刻離前緣更遠；從0.67L到翼梢，它的h／c比0.25T時刻更大.如圖9b所示，LEVd的截面環量Γz沿展向快速升高，在z＝0.8L處達到Γz，max后略微下降；在各個截面里，它的Γz比0.25T時刻更大.

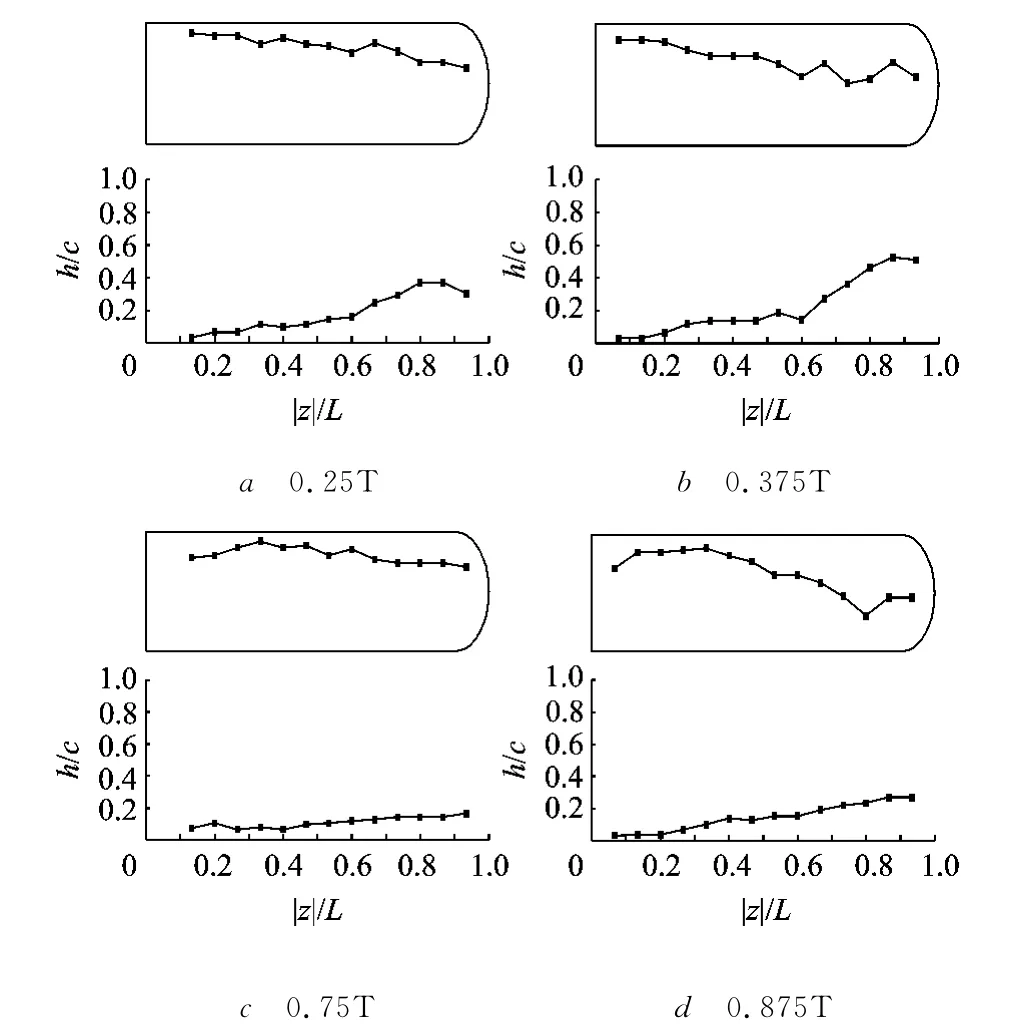
圖8 拍動翼LEV在翼面上的投影及距離翼面高度

圖9 拍動翼LEV的截面環量Γz

WTV的λci等值面不再像0.25T時刻那樣光滑，這是受到LEVd部分渦量脫落的影響.TEVd繼續向下游流動，比0.25T時刻離后緣更遠，新的TEVd從后緣脫落.

2.3 0.75T時刻的拍動翼流場

上拍前緣渦（LEVu，Leading Edge Vortex in the upstroking）從前緣z＝0.13L處開始形成（見圖6c）.但是它從z＝0.13L至0.47L的漩渦強度較弱，小于所選定的閾值，所以，在這幾個截面位置均沒有出現λci等值面.λci等值面顯示，LEVu的λci等值面比0.25T時刻LEVd的短，說明它的強度比0.25T時刻LEVd弱.ωz等值線（圖7c）顯示，0.75T時刻LEVu的空間結構也呈錐狀，但比0.25T時刻LEVd更扁更小.0.75T時刻LEVu之所以比0.25T時刻LEVd弱，是因為拍動翼在0.75T時刻的上拍迎角為30°，是0.25T時刻下拍迎角的一半.這減弱了翼面前緣的流動分離，削弱了拍動翼LEVu的強度.如圖8c所示，LEVu渦核線在翼面上的投影到前緣的距離基本保持不變；它到翼面的距離也基本保持不變.在外翼段，它比0.25T時刻LEVd的渦核線更貼近翼面.如圖9c所示，LEVu的Γz沿展向越來越大；從z＝0.47L開始，Γz迅速升高，并在翼梢處達到了Γz，max.

如圖6c所示，WTV的λci等值面順著來流向后伸展，并沒有像0.25T時刻那樣從翼梢卷起與拍動翼的上拍后緣渦（TEVu，Trailing Edge Vortex in the upstroking）相連.λci等值面顯示，拍動翼的尾跡比較復雜，在下拍結束后從后緣脫落下來的LEVd與剛從后緣脫落下來的TEVu纏繞在一起，在翼的前下方是下拍時脫落的TEVd.

2.4 0.875T時刻的拍動翼流場

LEVu從翼根開始形成，見圖6d.λci等值面顯示，LEVu的λci等值面比0.75T時刻LEVd長，說明它的漩渦強度比0.75T時刻LEVd強.｜ωz｜等值線（圖7d）顯示：在各個截面里，LEVu的渦量集中區比0.75T時刻更長更強；從z＝0.73L至翼梢，LEVu渦量集中區的中心逐漸遠離拍動翼前緣，在拍動翼前緣附近開始形成新渦量集中區.結合圖6d和圖7d可知，新渦量集中區的強度非常弱.如圖8d所示，拍動翼LEVu渦核線在翼面上的投影比0.75T時刻離前緣更遠，尤其在外翼段；它的h／c沿展向逐漸增大，在翼梢處達到0.2；在各個截面里，它的h／c比0.75T時刻更大，尤其在外翼段.如圖9d所示，LEVu的Γz沿展向迅速升高，在0.8L處達到Γz，max之后緩慢下降；在各個截面里，它的Γz比0.75T時刻更大.

WTV的λci等值面向下游伸展.拍動翼的尾跡與0.75T時刻的相比發生了明顯變化.TEVu與下拍結束時脫落的LEVd已經融合在一起.一個新的拍動翼TEVu開始從后緣脫落.TEVd仍然存在.

3 結 論

本文展示了兩個下拍拍動相位時刻（t＝0.25T，0.375T）和兩個上拍拍動相位時刻（t＝0.75T，0.875T）單個蜻蜓翼周圍的空間三維流動結構，并對這些三維流動結構隨拍動相位時刻的演變進行了研究.實驗結果分析表明：①拍動翼的前緣渦（LEV）結構成錐狀，由翼根向翼梢膨脹；其渦核線沿展向逐漸遠離前緣和翼面；其截面環量沿展向逐漸升高.②0.375T時刻的下拍前緣渦（LEVd）和0.875T時刻的上拍前緣渦（LEVu）分別比0.25T時刻的LEVd和0.75T時刻的LEVu更長更強.③0.25T時刻的LEVd比0.75T時刻的LEVu更強.④拍動翼的翼梢渦（WTV）從拍動翼的迎風面向背風面卷起；下拍的WTV（0.25T和0.375T）與下拍后緣渦（TEVd）連接；上拍的 WTV（0.75T和0.875T）沿流向向下游伸展.⑤下拍后緣渦（TEVd）比上拍后緣渦（TEVu）更強；TEVu與從翼面脫落下來的LEVd相遇并融合.

（References）

［1］Norberg R A.Hovering flight of the dragonfly Aeschna juncea L ［M］／／New York：Plenum Press，1975：763－781

［2］Maybury W J，Lehmann F O.The fluid dynamics of flight control by Kinematic phase lag variation between two robotic insect wings［J］.Journal of Experimental Biology，2004，207（26）：4707－4726

［3］Sun M，Lan S L.A computational study of the aerodynamic forces and power requirements of dragonfly （Aeschna juncea）hovering ［J］.Journal of Experimental Biology，2004，207（11）：1887－1901

［4］Lan S L，Sun M.Aerodynamic force and flow structure of two airfoils in flapping motions［J］.Acta Mechanica Sinica，2001，17（4）：310－331

［5］Wang J K，Sun M.A computational study of the aerodynamics and forewing-hindwing interaction of a model dragonfly in forward flight［J］.Journal of Experimental Biology，2005，208（19）：3785－3804

［6］Huang H，Sun M.Dragonfly forewing-hindwing interaction at various flight speeds and wing phasing ［J］.AIAA Journal，2007，45（2）：508－511

［7］姚大鵬，申功炘，朱百六，等.機械蜻蜓懸停時的氣動力實驗研究［J］.實驗流體力學，2011，25（1）：69－75

Yao Dapeng，Shen Gongxin，Zhu Bailiu，et al.Force measurement of hovering dragonfly via an electromechanical model［J］.Journal of Experiments in Fluid Mechanics，2011，25（1）：69－75（in Chinese）

［8］孫茂，黃華.微型飛行器的仿生力學 ——蝴蝶飛行的氣動力特性［J］.北京航空航天大學學報，2006，32（10）：1146－1151

Sun Mao，Huang Hua.Biomimetic mechanics of micro-air vehicles—the aerodynamic force of butterfly in forward flight［J］.Journal of Beijing University of Aeronautics and Astro-nautics，2006，32（10）：1146－1151（in Chinese）

［9］孫茂，吳江浩.昆蟲飛行的高升力機理和能耗［J］.北京航空航天大學學報，2003，29（11）：970－977

Sun Mao，Wu Jianghao.Unsteady lift mechanisms and energetic in flying insects ［J］.Journal of Beijing University of Aeronautics and Astronautics，2003，29（11）：970－977（in Chinese）

［10］Wu T Y.Fish swimming and bird／insect flight［J］.Annual Review of Fluid Mechanics，2011，43：25－58

［11］Shyy W，Aono H，Chimakurthi S K，et al.Recent progress in flapping wing aerodynamics and aeroelasticity ［J］.Progress in Aerospace Sciences，2010，46（7）：284－327

［12］Alexander D E.Unusual phase relationships between the forewings and hindwings in flying dragonflies［J］.Journal of Experimental Biology，1984，109（1）：379－383

［13］牟曉蕾，孫茂.昆蟲翅平面形狀和展弦比對其氣動性能的影響［J］.北京航空航天大學學報，2011，37（11）：1359－1364

Mou Xiaolei，Sun Mao.Effects of wing planform on aerodynamics force production of stroking model insect wing［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（11）：1359－1364

［14］Lu Y，Shen G X，Lai G J.Dual leading-edge vortices on flapping wings［J］.Journal of Experimental Biology，2006，209（24）：5005－5016

［15］Wakeling J M，Ellington C P.Dragonfly flight I gliding flight and steady-state aerodynamic forces ［J］.Journal of Experimental Biology，1997，200（3）：543－556

［16］Okamoto M，Yasuda K，Azuma A.Aerodynamic characteristics of the wings and body of a dragonfly［J］.Journal of Experimental Biology，1996，199（2）：281－294

［17］Lan S L，Sun M.Aerodynamic properties of a wing performing unsteady rotational motions at low Reynolds number［J］.Acta Mechanica，2001，149（1－4）：135－147

［18］Willmott A P，Ellington C P.The mechanics of flight in the Hawkmoth manduca Sexta .1.Kinematics of hovering and forward flight［J］.Journal of Experimental Biology，1997，200（21）：2705－2722

［19］賴國俊，申功炘.控制點排列對圖像校正的影響及重復校正［J］.北京航空航天大學學報，2009，35（10）：1214－1219

Lai Guojun，Shen Gongxin.Image mapping approach based on biharmonic spline interpolation concerning dot arrangement and multi-mapping［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35（10）：1214－1219（in Chinese）

［20］Zhou J，Adrian R J，Balachandar S，et al.Mechanisms for generating coherent packets of hairpin vortices in channel flow ［J］.Journal of Fluid Mechanics，1999，387：353－396

［21］吳介之，馬暉揚，周明德.渦動力學引論 ［M］.北京：高等教育出版社，1993

Wu Jiezhi，Ma Huiyang，Zhou Mingde.Introduction to vorticity and vortex dynamics［M］.Beijing：Higher Education Press，1993（in Chinese）

［22］童秉綱，尹協遠，朱克勤.渦運動理論 ［M］.2版.合肥：中國科學技術大學出版社，2009

Tong Binggang，Yin Xieyuan，Zhu Keqin.Theory of vortex dynamics［M］.2nd ed.Hefei：China University of Science and Technology Press，2009（in Chinese）