提高電動加載系統輸出平滑的CMAC復合控制

楊 波 程 龍

（北京航空航天大學 自動化科學與電氣工程學院，北京 100191）

電動加載系統用于在實驗室條件下模擬飛行器在飛行過程中舵面所受的氣動載荷，可以將經典的全實物實驗轉化為實驗室條件下的半物理預測性實驗，具有縮短研制周期、節約成本、提高可靠性和成功率的優點.

由于電動加載系統中不可避免地存在飽和、摩擦、間隙、彈性形變等非線性因素［1］及多余力矩的影響，傳統控制方法的控制結果往往達不到理想效果，引入智能控制策略來代替傳統控制方法成為了相關研究的重點.其中CMAC（Cerebellar Model Articulation Controller）控制策略因其學習速度快、能夠克服局部最優問題、適用于在線學習且易于硬件實現而成為硬件平臺算法的研究重點［2］，目前常用的是 CMAC和 PD（Proportional Derivative）的復合控制策略.

文獻［3］將CMAC＋PD復合控制器應用于電動加載系統，仿真結果表明了CMAC＋PD復合控制在抑制多余力矩方面有很好的效果；文獻［4－5］對基于CMAC＋PD復合控制的電動加載系統進行了穩定性和動態特性的分析，實驗結果表明CMAC＋PD復合控制算法滿足電動加載系統實時控制的要求，并且可以大幅提高電動加載系統的魯棒性和穩態精度.

盡管CMAC＋PD復合控制策略在穩態精度和實時控制上有很好的表現，但與單獨使用PID控制相比，CMAC＋PD復合控制策略在快速減小誤差的同時會使輸出波形的平滑性變差，在進行電動加載系統實驗驗證時，輸出不平滑會導致電機頻繁往復轉動，使電機發生抖動，影響控制精度、加載頻寬和電機的壽命.所以如何提高CMAC＋PD復合控制輸出的平滑性就成為影響其進入實用階段的關鍵問題.

國內外現階段關于CMAC＋PD復合控制電動加載系統的研究大多停留于仿真階段，沒有實現對電機的實際控制，所以對于其控制電動加載系統平滑性方面的研究較少.由于CMAC算法的輸出是由權值決定的，所以對權值進行平滑將直接影響輸出結果.在CMAC權值平滑方面，文獻［6－7］分別采用二次樣條基函數和高斯基函數來替代傳統CMAC的矩形基函數更新權值，以達到平滑輸出的目的；文獻［8］提出將每個權值向全部權值的均值接近，減少權值間差異的方法進行平滑.盡管這些算法都有助于提高CMAC的輸出平滑性，但這些算法本質上都是在權值更新后再對權值進行平滑，平滑效果有限.

本文通過分析CMAC算法權值調整指標與輸出平滑性的關系，提出了提高CMAC輸出平滑性的改進算法，該算法在權值調整指標中同時考慮誤差和相鄰權值間差異的影響，推導出一個新的權值更新公式，在權值更新時直接達到減小誤差和增進平滑性的目的.通過仿真和實驗證明，這種新算法對于提高電動加載系統控制精度和平滑性有很好的效果.

1 CMAC＋PD復合控制原理

CMAC的結構如圖1所示，它由網絡輸入、概念映射、物理映射和網絡輸出4個基本部分組成.圖1中，輸入向量X中的每一個點都與概念存儲空間P中的C個存儲單元相對應，然后這C個存儲單元又與物理映射w的C個單元對應，而神經網絡的輸出Y就是這C個物理存儲單元中權值之和.

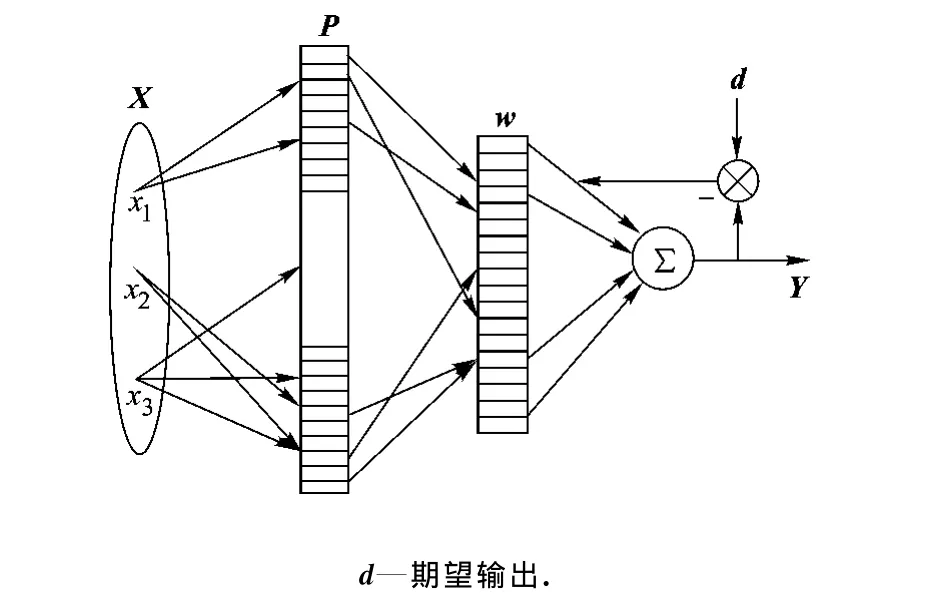
圖1 CMAC結構圖

基于CMAC＋PD復合控制的電動加載系統控制器結構如圖2所示，其中CMAC以誤差作為訓練信號來調整CMAC的權值，實現前饋控制，確保系統的響應速度，減少超調量.常規PD算法實現反饋控制，以保證系統的穩定性.

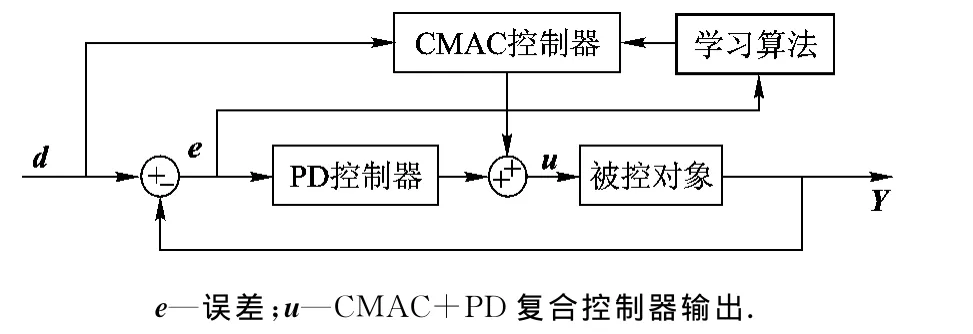
圖2 CMAC＋PD復合控制器結構圖

2 復合控制輸出平滑性問題分析

目前CMAC＋PD復合控制的研究重點在穩態精度、穩定性和多余力矩抑制方面，在控制電動加載系統時的平滑性方面研究很少.但CMAC＋PD復合控制法與普通PID控制法相比，存在輸出不平滑的問題，圖3、圖4是CMAC＋PD復合控制算法（簡稱CMAC＋PD算法）和普通PID控制電動加載系統在0.5Hz下跟蹤幅值為5N·m的正弦信號時的測試結果.可以發現單獨使用PID控制電動加載系統時盡管穩態精度不高，但輸出波形較為平滑，而使用CMAC＋PD算法時，盡管穩態精度較好，但輸出波形卻不平滑，波形有很大波動.這種波動在仿真時不明顯，但是實際控制電機時，這種輸出的增減趨勢的頻繁變化會導致電機頻繁往復而產生抖動，這種抖動對控制精度、加載頻寬和電機的壽命都有不利的影響.因此有必要對CMAC＋PD算法進行改進以保持較好的穩態精度的同時提高輸出的平滑性.

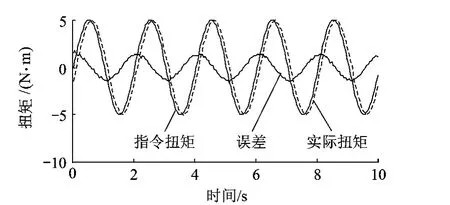
圖3 PID在0.5Hz下測試結果

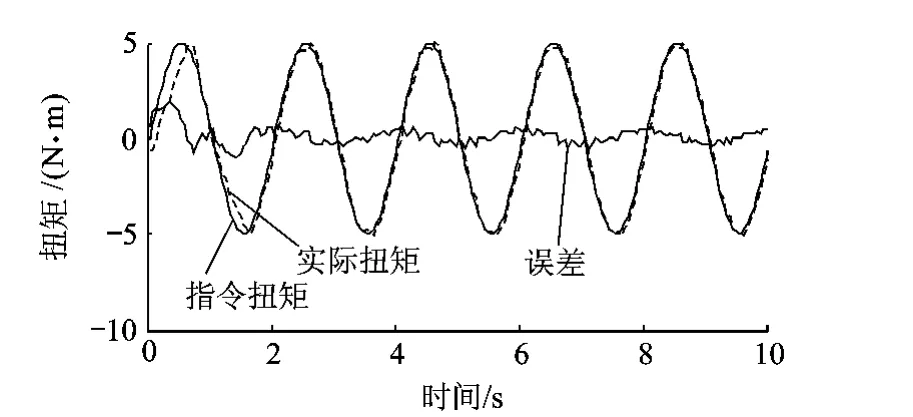
圖4 CMAC＋PD算法在0.5Hz下測試結果

3 改進的CMAC算法及仿真分析

3.1 改進的CMAC算法

由傳統CMAC計算原理可知，每一個輸出都與物理存儲空間w中的C個權值關聯，這些權值的和構成了輸出

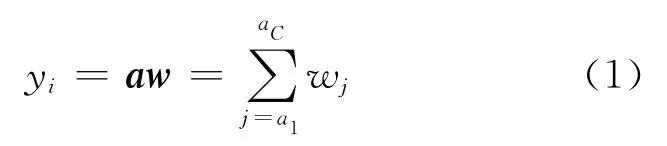
式中，行向量a中有C個值為1，其余為0，用于表示輸出yi與w的關聯關系.定義Y為輸出向量，A為對應的選擇矩陣，則Y可以表示成

由式（2），可以得到誤差向量：

傳統的CMAC權值調整公式為

式中，R為單位矩陣.

權值更新公式為

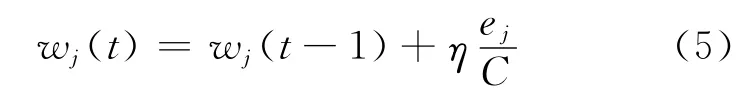
式中，η為學習率.

傳統的CMAC權值更新算法僅僅根據誤差來更新權值，由于CMAC相近的輸入激發相鄰的權值的性質，相鄰權值間的差異也會隨誤差變大，導致由式（1）計算的輸出的差距變大，使輸出更加不平滑，進而影響PD的輸出使CMAC＋PD算法的不平滑現象加劇.

當CMAC應用于仿真時，這種輸出的變化雖然會導致輸出波形不平滑，但有利于快速的減小誤差，取得更好的穩態精度.但是當CMAC應用于實驗控制加載電機時，系統中的非線性因素會加劇輸出的頻繁變化，直接導致電機抖動，造成誤差加大甚至有可能損傷電機.因此針對電動加載系統實驗的實際情況，需要對CMAC的權值更新方法進行修改，以增加輸出的平滑性.

由于在滿足誤差減小的同時，一定存在一組變化最小即代價最小的權值，使輸出滿足誤差最小且輸出平滑需要.基于這個思想，現在使用新的權值調整式（6）來考慮新的權值更新方法，該公式同時考慮了誤差和臨近權值差異，通過調整權值更新公式以獲得式（6）的最小值，可以使CMAC算法在獲得更小誤差的同時減小相鄰權值間的差異，以獲得更平滑的輸出.

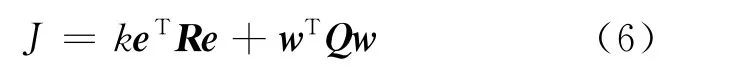
其中，k為誤差在權值調整指標中的比重系數；Q為一個對稱的三對角矩陣：

wTQw是相鄰權值的差的平方和：

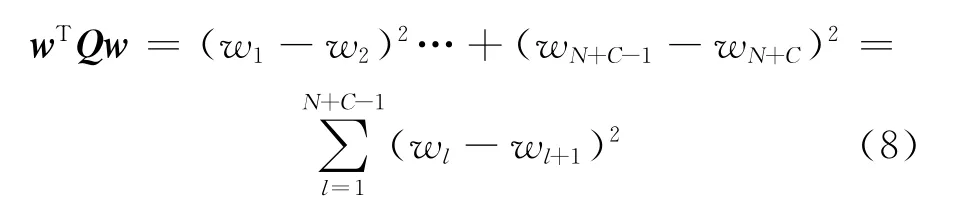
為了找到權值的最優解，對J關于w求偏導，并使偏導為0，有

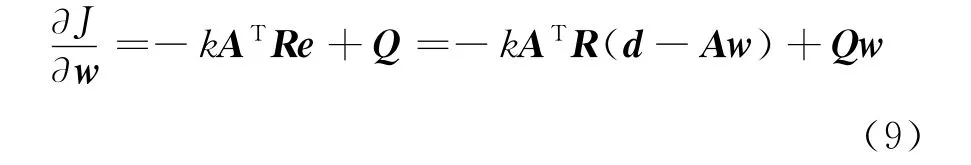
式（9）可化簡為

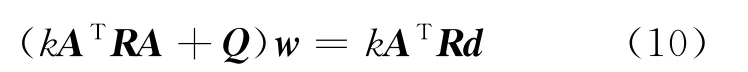
解得

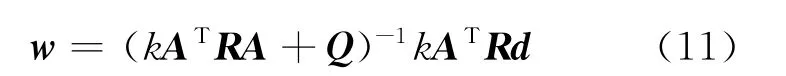
由于電動加載系統使用單輸入單輸出的CMAC算法，因此式（11）可以進一步簡化為如下形式：

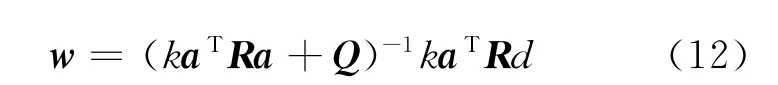
新權值更新公式（12）同時考慮了減小誤差和增加平滑性，替代了原來的增量式公式.

3.2 改進的CMAC算法仿真及結果分析

以文獻［9］中的電動加載系統模型為基礎進行仿真，采用如圖2所示的CMAC＋PD復合控制結構.其中PD參數設定為KP＝1，KD＝0.05；CMAC的參數設定為：量化參數N＝100，C＝15，η＝0.2，k＝6.

現在對傳統CMAC＋PD算法和本文的改進算法進行仿真比較，加載指令設置為

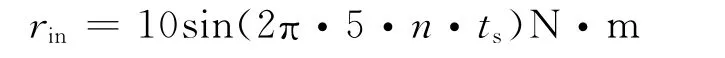
式中，ts為采樣周期1ms；n為仿真步長.并加入多余力矩干擾信號：

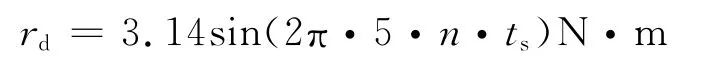
仿真結果的誤差比較如圖5所示.

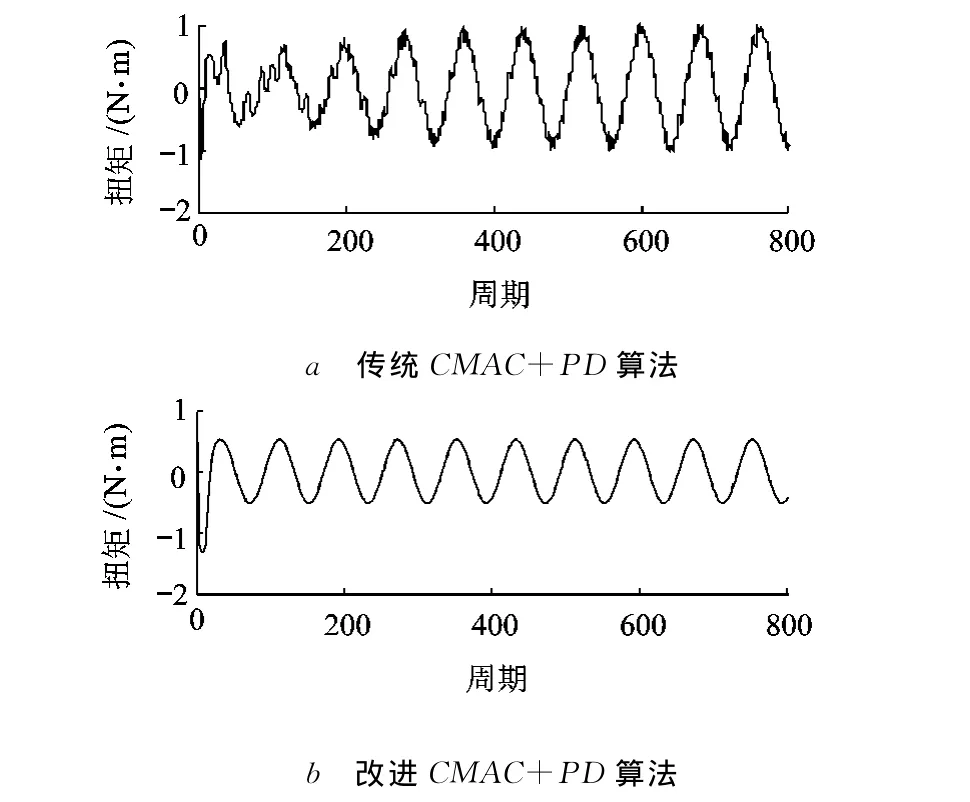
圖5 仿真結果的誤差比較

從圖5可以看出，傳統CMAC＋PD算法在仿真過程中初始誤差幅值大約0.5N·m，但是隨著仿真的進行誤差增大，且波形不夠平滑.使用改進CMAC＋PD算法誤差較小，穩態誤差幅值大約0.44N·m，且波形平滑.

仿真結果表明改進CMAC＋PD算法在控制電動加載系統的穩態精度和平滑性上都有很大改進.

4 改進CMAC算法實驗驗證及分析

本文利用實驗室的電動加載系統來驗證改進CMAC＋PD算法的有效性，該系統由力矩電機、DSPF28335、扭矩傳感器、驅動器、調理電路和上位機組成，系統的總體結構如圖6所示.

圖6 舵面電動加載系統結構圖

實驗測試的參數與仿真參數保持一致，加載指令幅值為5N·m的正弦信號，頻率f分別選擇1.0，1.5，2.0Hz.傳統CMAC＋PD算法和改進CMAC＋PD算法的實驗測試數據結果如圖7～圖12所示.

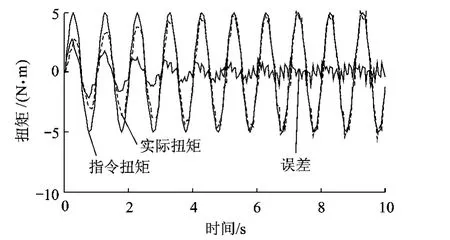
圖7 傳統CMAC＋PD算法在1Hz頻率下加載結果

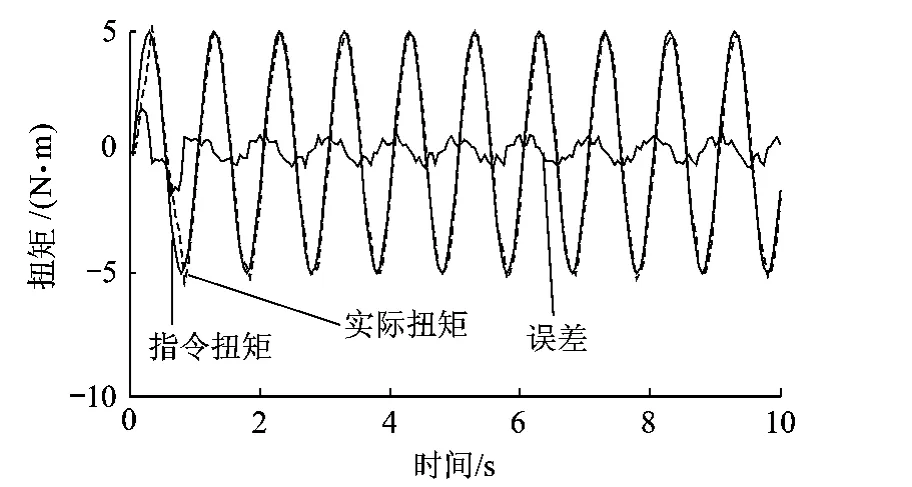
圖8 改進CMAC＋PD算法在1Hz頻率下加載結果

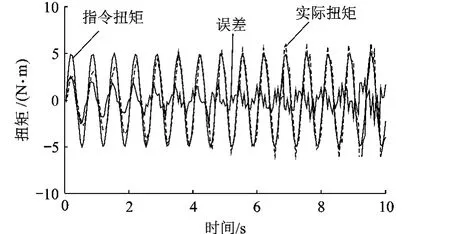
圖9 傳統CMAC＋PD算法在1.5Hz頻率下加載結果

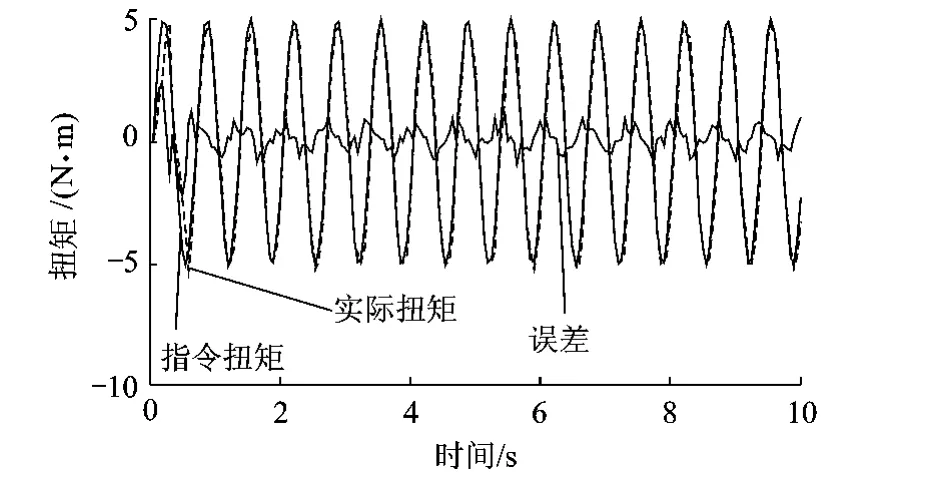
10 改進CMAC＋PD算法在1.5Hz頻率下加載結果

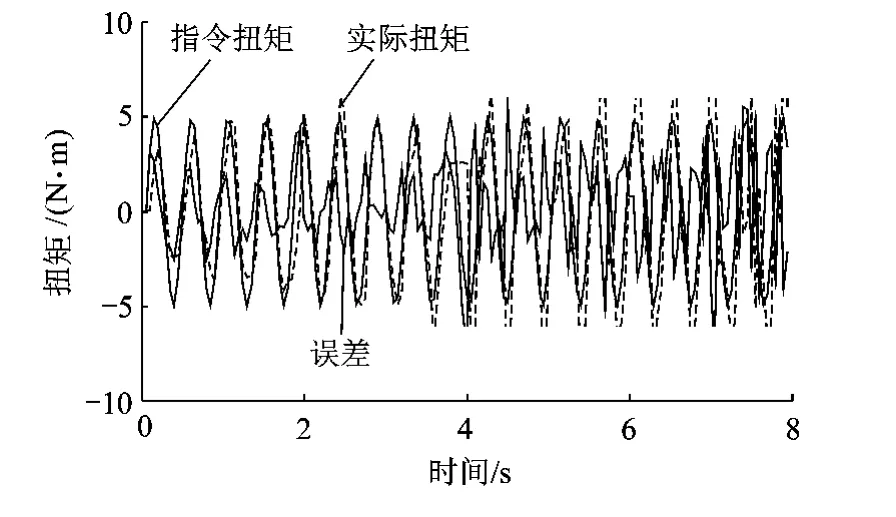
圖11 傳統CMAC＋PD算法在2Hz頻率下加載結果

改進CMAC＋PD 算法在1.0，1.5，2.0Hz頻率下5s后的最大誤差幅值為0.93，1.11，1.57 N·m，而傳統CMAC＋PD算法在1.0Hz頻率下5s后的最大誤差幅值為1.19N·m，在1.5，2.0Hz頻率下5s時已有發散趨勢.實驗結果表明改進CMAC＋PD算法與傳統CMAC＋PD算法相比有更好的穩態精度和穩定性，且從誤差波形可以看出，改進CMAC＋PD算法的輸出波形更加平滑.

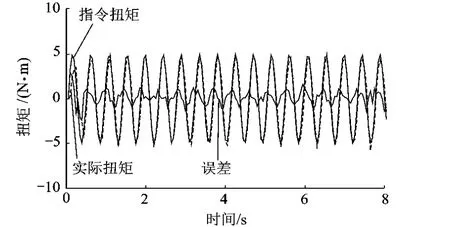
圖12 改進CMAC＋PD算法在2Hz頻率下加載結果

對加載平臺施加幅值為5N·m，頻率為1Hz的60s的正弦信號，并通過在加載過程中扳動連接軸來施加位置干擾，加載結果的誤差如圖13所示.施加的干擾分別為13s及30s附近的兩次小幅度干擾和45s及50s附近的兩次大幅度干擾.可以觀察到在干擾移除后控制策略能很快恢復穩定狀態，具有很好的魯棒性和抗干擾性.

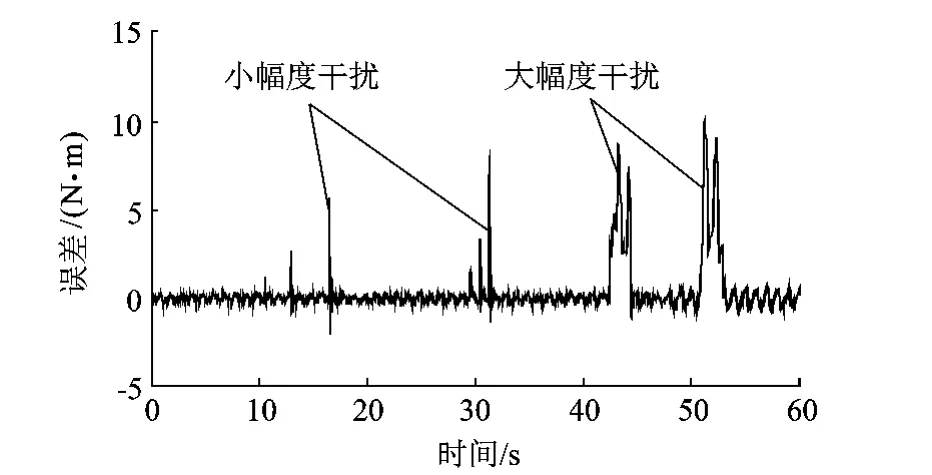
圖13 改進CMAC＋PD算法在干擾下加載的誤差結果

5 結 論

本文對傳統CMAC＋PD復合控制應用于電動加載系統時輸出不平滑的影響因素和危害進行了分析，提出了一種同時滿足減小誤差和輸出平滑性要求的改進CMAC＋PD復合控制算法.該算法通過新的權值調整指標推導出了新的權值更新公式，在權值更新時直接達到減小誤差和增進平滑性的目的.仿真和實驗結果表明，與傳統的CMAC＋PD復合控制算法相比，該改進CMAC＋PD復合控制算法能有效提高控制電動加載系統時的穩態精度和輸出平滑性，并且具有良好的魯棒性和抗干擾能力，更適用于電動加載系統的控制.

（References）

［1］王瑞，陳松林.電動負載模擬器輸出力矩的影響因素分析［J］.測試技術學報，2011，25（1）：47－51

Wang Rui，Chen Songlin.Analysis of influence factors on output moment of electrical lord simulator［J］.Journal of Test and Measurement Technology，2011，25（1）：47－51（in Chinese）

［2］李守奇.基于CMAC與PID的無刷直流電機復合控制算法仿真［J］.科教新報，2011（3）：254－255

Li Shouqi.Composite control of brushless DC motor based on CMAC and PID algorithm simulation［J］.Science and Education，2011（3）：254－255（in Chinese）

［3］楊波，王俊奎.無人機舵面負載模擬系統的小腦模型控制［J］.北京航空航天大學學報，2009，35（11）：1361－1365

Yang Bo，Wang Junkui.CMAC neural network for the rudder dynamic load simulator of unmanned aerial vehicles［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35（11）：1361－1365（in Chinese）

［4］王剛，李建府，朱榮剛.CMAC改進算法在電動負載模擬器的應用［J］.電光與控制，2011，18（4）：72－76

Wang Gang，Li Jianfu，Zhu Ronggang.Application of an improved arithmetic based on CMAC in electrical load simulator［J］.Electronics Optics and Control，2011，18（4）：72－76（in Chinese）

［5］楊波，黃耀達，臺鈺瑩.基于BOWA小腦模型的高精度穩定電動加載系統［J］.航空學報，2012，33（4）：734－743

Yang Bo，Huang Yaoda，Tai Yuying.High precision and stable electric loading system based on BOWA-CMAC［J］.Acta Aeronautica et Astronautica Sinica，2012，33（4）：734－743（in Chinese）

［6］Wang S Y，Tseng C L，Yeh C C.Adaptive supervisory Gaussian-cerebellar model articulation controller for direct torque control induction motor drive［J］.Electric Power Applications，2011，5（3）：295－306

［7］Fu Yanli，Li Shijing，Xiao Yunshi.Study on new neural network adaptive control of industrial manipulators based on desired compensation［C］／／Song Jian.7th World Congress on Intelligent Control and Automation.Chengdu：IEEE，2008：6983－6987

［8］Ge Yingqi，Luo Xiaoping，Du Pengying.A new improved CMAC neural network［C］／／Wang Fuli.22nd Chinese Control and Decision Conference.Xuzhou：IEEE，2010：3271－3274

［9］楊波，王俊奎.基于改進的CMAC的電動加載系統復合控制［J］.航空學報，2008，29（5）：1314－1318

Yang Bo，Wang Junkui.Hybrid control based on improved CMAC for motor-driven loading system［J］.Acta Aeronautica et Astronautica Sinica，2008，29（5）：1314－1318（in Chinese）