低雷諾數圓柱繞流的大渦模擬分析

李 霖，張志國，王先洲，馮大奎

(華中科技大學船舶與海洋工程學院，湖北武漢430074)

0 引言

一個世紀以來，圓柱繞流問題一直是經典的流體力學問題之一，也是眾多理論分析、數值模擬以及實驗研究的對象［1-2］。盡管研究歷經時間如此之長，但這種最簡單的流動現象物理本質的理解依然不完整。閔強利［3］計算了2種雷諾數Re=200，800情況下的圓柱繞流，發現在Re=200時產生的卡門渦街非常規則，而隨著雷諾數的增加，Re=800時，渦街出現不規則現象，并表現出三維效應。文獻 ［4-5］研究了不同截面形狀在低雷諾數下的繞流場，并重點研究了阻力、升力的周期性變化特性。

隨著計算機硬件的不斷發展，大渦模擬作為一種新的湍流模型相比原來的湍流模型在求解非穩態流動方面具有巨大的潛力。大渦模擬方法的基本思想是用瞬時的N-S方程直接模擬計算湍流中的大尺度渦，而小尺度渦對大渦的影響則通過建立近似的模型來考慮，這種影響模型稱為亞格子尺度模型。王漢青［6］等人介紹了大渦模擬的理論進展和發展趨勢，描述了當前大渦模擬在工程中的具體應用。指出大渦模擬在模擬計算從層流到湍流轉換、非定常湍流和高速湍流方面具有其他湍流模型無可比擬的優勢。傅慧萍［7］以潛艇模型SUBOFF為研究對象，采用大渦模擬 (LES)方法求解了流動的非定常解。通過與試驗值以及采用RNGk-ε湍流模型得到的定常結果比較，驗證了大渦模擬方法的有效性。

本文采用大渦模擬方法求解低雷諾數下的圓柱繞流場，研究卡門渦街的周期性特性。對一個完整的渦街脫落周期進行詳細討論，揭示了不同時刻旋渦的生成、發展、脫落和演化過程。通過研究圓柱表面的壓力變化說明產生周期性脫落渦對的原因，以及產生周期性變化的升、阻力的原因。

1 數值算法

自然界中的流動現象基本可以通過基于連續性假設的納維葉-斯托克斯方程 (N-S方程)來描述。在應用于大渦模擬方法時，需要對N-S方程進行一定過濾處理。

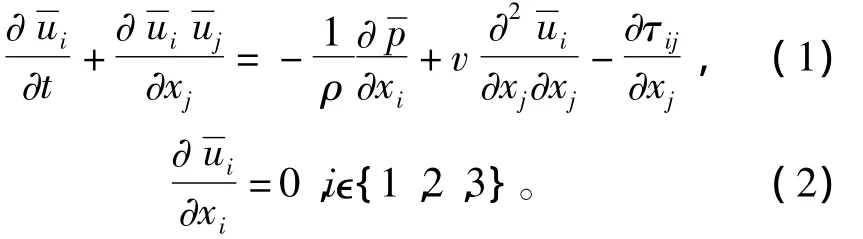
對于亞格子尺度模型［8］，采用標準 Smagorinsky［9］模型的方法。

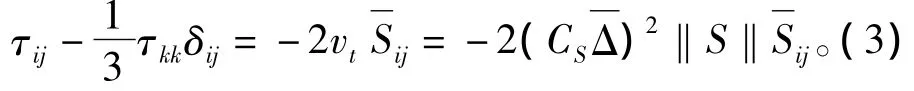
式中，vol是計算單元的體積。

亞格子尺度可表示為

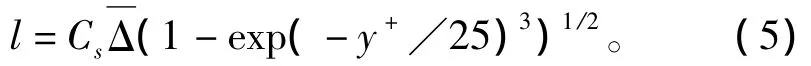
式中，Smagorinsky 常量 Cs取為 0.255［10］。

2 計算模型

本文所采用的計算模型為直徑D=0.04 m的圓柱。來流速度為U=0.01 m/s，計算的雷諾數Re=400。計算域為方形，沿著來流方向長度為7.5D，尾流去流段長度為40D，兩側寬度為7.5D。流動在選定的計算域內能夠充分發展，圓柱周圍采用邊界層網格，能夠捕捉圓柱周圍的細微流動。圖1為計算域示意圖，圖2為圓柱周圍的網格劃分。

3 計算結果與分析

3.1 計算結果與實驗結果對比

表1為計算所得的斯特勞哈爾數(St)以及阻力系數(Cd)與文獻中實驗結果的對比。

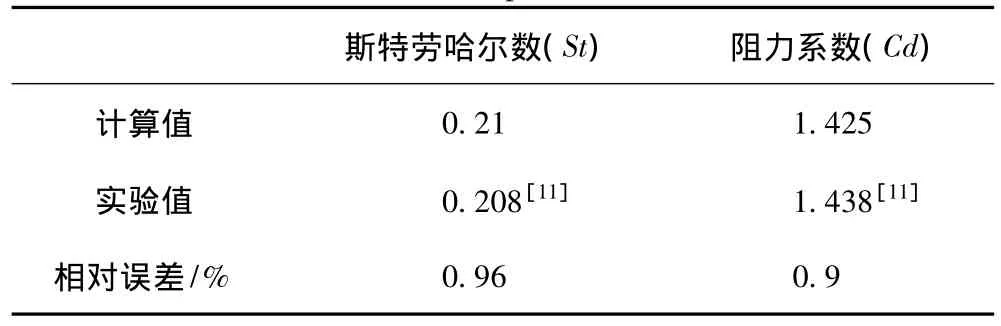
表1 實驗結果與計算結果Tab.1 Results from experiment and simulation

計算結果與實驗結果吻合良好，說明采用本文的數值計算方法是準確而可靠的。

3.2 渦街脫落

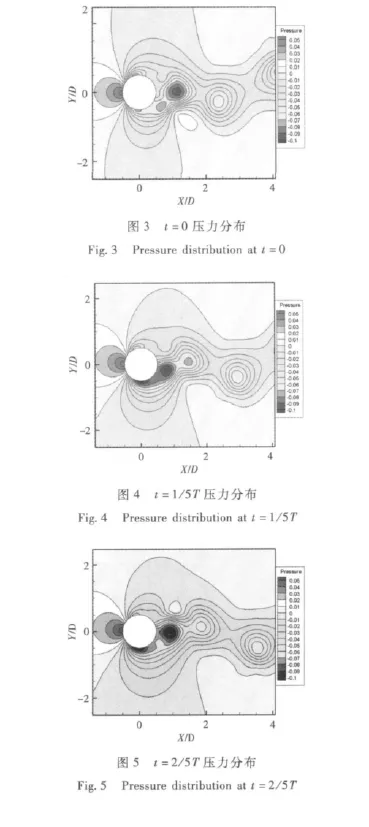
圖3～圖8為圓柱繞流非穩態流動中一個典型的渦街脫落周期中不同時刻圓柱周圍的壓力場分布。反映了一個典型渦街脫落周期內漩渦的初生、形成、脫落及在尾流中不斷發展的整個過程。從圖3可看出，t=0時刻，上一周期脫落形成的渦在圓柱尾流中逐漸發展，圓柱的右下方約45°的位置形成一片明顯的負壓區，旋渦在負壓區內逐漸生成。圖4中t=1/5T時刻，圓柱右下方的漩渦完全生成，沿著尾流方向移動，并有逐步脫落的趨勢。而圖5中t=2/5T時刻，圓柱右下方形成的漩渦完全脫落并沿著尾流方向發展。圖6中t=3/5T時刻，之前由圓柱右下方脫落的漩渦在尾流中逐漸發展，同時在圓柱的右上方約45°的位置形成一片負壓區，旋渦在負壓區內逐漸生成。圖7中t=4/5T時刻圓柱右上方的漩渦完全生成，沿著尾流方向移動，并有逐漸脫落的趨勢。最后圓柱右上方形成的漩渦在t=T時刻完全脫落 (圖8)，脫落的漩渦在尾流中不斷發展，改變著圓柱周圍的壓力場分布。圓柱右上方區域和右下方區域形成的漩渦交替脫落，在尾流中不斷發展，形成了典型的卡門渦街。

3.3 水動力特性

圓柱在繞流場中受到的主要水動力為阻力和升力。通過無量綱化，可以用阻力系數Cd及升力系數CL來表征。

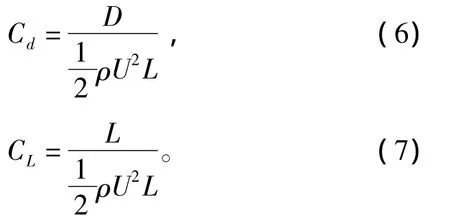
式中:D和L分別為圓柱所受的阻力和升力;U為來流速度;ρ為流體密度;L為特征長度，本文取為圓柱直徑。

圖9為計算求取的穩定的非穩態計算時間內圓柱的阻力系數、升力系數時程曲線。計算時時間步長取為0.05 s。計算所得的結果是在非穩態計算了較長時間，流動發展相對較為穩定時提取出來的。

圖9 阻力系數和升力系數時程曲線Fig.9 Time-history curve of drag and lift coefficient

由圖9可知阻力和升力都呈現周期性的變化，這是由于周期性脫落的卡門渦街引起的。周期性脫落的漩渦造成了圓柱周圍壓力場的不斷變化。升力系數基本在0左右波動，而阻力系數基本在1.4左右波動，這說明阻力對圓柱的作用非常強，升力對圓柱的作用一般。文獻［11］指出，升力以斯特勞哈爾渦泄頻率fs變化，阻力以2倍渦泄頻率2fs變化。由圖9可以看出，阻力變化的頻率是升力變化頻率的2倍。進一步對升力做功率譜密度分析，可以得到渦泄頻率fs，圖10為升力功率譜密度。圖10中的尖峰對應為斯特勞哈爾渦泄頻率fs，其值在0.05 Hz附近，與文中之前計算的斯特勞哈爾數 (St=fs*D/U)是對應的。

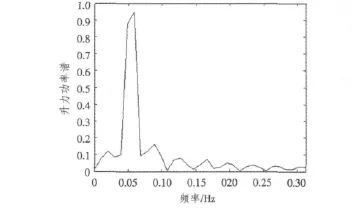
圖10 升力功率譜密度Fig.10 The power spectral density of lift

為了深入研究圓柱上阻力和升力脈動的變化，可以研究圓柱瞬態的升力、阻力系數。非穩態阻力系數可以定義為

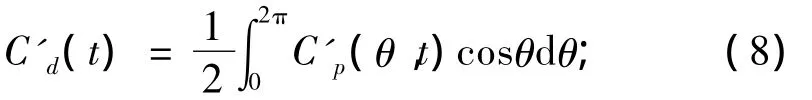
非穩態升力系數可以定義為

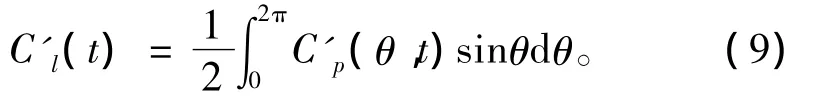
角度θ的定義見圖11;圖12為典型的渦街脫落周期中不同時刻圓柱周向的壓力系數變化。

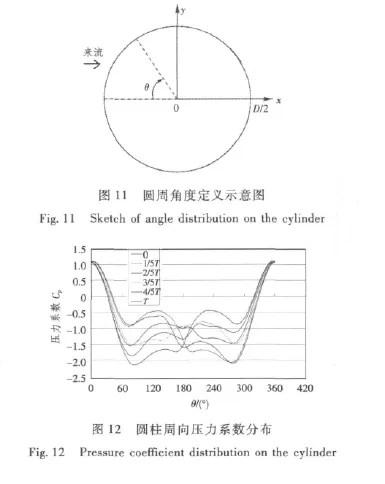
圖12可看出，圓柱壓力系數在1個周期內變化基本是對稱的。圓柱駐點處(θ=0°和θ=360°)壓力系數Cp有最大值，在1附近;隨著來流向圓柱兩側擴展，壓力系數迅速減小。在θ=80°和θ=280°附近，流動產生分離，圓柱駐點后方的壓力在不同時刻呈現出較為規律的周期性變化。對比t=1/5T和t=4/5T時刻可以看出，在t=1/5T時刻圓柱的右下方區域 (180°～270°)的壓力大于右上方區域(90°～180°)，此時圓柱具有最大的負升力;在t=4/5T時刻圓柱的右下方區域 (90°～180°)的壓力大于右下方區域 (180°～270°)，此時圓柱具有最大的正升力。這樣升力就完成了1個渦街脫落周期中由最大正升力向最大負升力的轉變。上述過程不斷進行，就形成了升力的周期性變化。

4 結語

采用大渦模擬的方法研究了雷諾數Re=400的圓柱繞流場，準確捕捉了卡門渦街這一經典流動現象，同時通過對水動力特性的研究，得出以下結論:

1)采用大渦模擬的方法進行低雷諾數圓柱繞流場的研究是準確可靠的，大渦模擬作為一種新的湍流模型是值得深入研究和普遍運用的;

2)圓柱的渦泄頻率是和圓柱的升力功率譜相互對應;

3)圓柱表面壓力的周期性變化是誘發漩渦周期性生成和脫落的原因。

本文僅用大渦模擬對二維圓柱進行了繞流場的分析，但實際的流動都是具有三維效應的，故今后將運用大渦模擬對圓柱的三維繞流場繼續研究。

［1］MAIR W A.Bluff bodies and vortex shedding［J］.Journal of Fluid Mechanics.，1971，45:209-224.

［2］MUJUMDAR A S.，DOUGLAS W J M.Vortex shedding from slender cylinders of various cross sections［J］.Journal of Fluids Engineer，1973，95(3):474-476.

［3］閔強利.低雷諾數卡門渦街數值模擬［J］.四川兵工學報，2009，30(11):81-84.MIN Qiang-li.Simulation of Karman Vortex Street at low Reynolds number［J］.Journal of Sichuan Ordnance，2009，30(11):81-84.

［4］LEI Yue.Investigation of the flow and heat transfer around cylinders at low Re［J］.Advanced Materials Research，2011，156-157:1630-1634.

［5］BOGRAD D D，GARRISON D H.Moment and heat transfer from cylinders in laminar cross-flow at 10-4≤Re≤200［J］.International Journal of Heat and Mass Transfer，1998，41(22):3409-3430.

［6］王漢青，王志勇，寇廣孝.大渦模擬理論進展及其在工程中的應用［J］.流體機械，2004，32(7):23-27.WANG Han-qing，WANG Zhi-yong，KOU Guang-xiao.Theoretical development and application of Large Eddy Simulation in engineering［J］.Fluid Machinery，2004，32(7):23-27.

［7］傅慧萍，繆國平，大渦模擬在噪聲計算中的應用［J］.上海交通大學學報，2009，43(8):1307-1312.FU Hui-ping，MIAO Guo-ping.Application of LES method to flow noise calculation［J］.Journal of Shang hai Jiaotong University，2009，43(8):1307-1312.

［8］FENG W，FERNANDO，STOLL R.Evaluation of dynamic subgrid-scale models in large-eddy simulations of neutral turbulent flow over a two-dimensional sinusoidal hill［J］.Atmospheric Environment，2007，41(13):2719-2728.

［9］BOGEY C，BAILLY C.Large eddy simulations of round free jets using explicit filtering with/without dynamic Smagorinsky model［J］.International Journal of Heat and Fluid Flow，2006，27:603-610.

［10］MOIN P，KIM J.Numerical investigation of turbulent channel flow［J］.Journal of Fluid Mechanics，1982，118:341-377.

［11］SCHLICHTING H.邊界層理論［M］.北京:科學出版社，1979.SCHLICHTING H.Theory of boundary layer［M］.Beijing:Science Press，1979.