空間單位區域雙二次有理貝賽爾曲面混沌特性研究
于萬波周洋
(大連大學信息工程學院,大連 116622)
1 引言
目前,混沌現象的研究仍然在繼續,從發現混沌現象到對混沌進行數學描述,從混沌控制到混沌同步再到系統的混沌化,研究人員一直在混沌的各個分支領域進行研究,取得了許多有價值的結果[1-8].系統混沌化是目前混沌領域的研究熱點問題之一,通過修改系統的參數或者重新構造系統等使其出現混沌.混沌化的研究可以產生混沌序列用于圖像加密等,也可以利用產生的混沌系統進行液體氣體混合等實際工作領域.基于混沌本質的探索以及混沌化的需要,文獻[9—15]對混沌的本質以及混沌化的一些方法進行了研究,給出了一些混沌化的新方法.文獻[16]研究了調整小波函數使其混沌化的問題,文獻[17]研究了平面單位區域內二次函數的混沌特性,得到的結論是標準二次映射是Li-Yorke混沌的,也是Devaney混沌的.事實上,在滿足一定條件的情況下,還存在大量的二次函數是混沌的.二次函數都可以使用平移與縮放等變換化為標準二次函數,其混沌特性不變.對單位區域上的非標準二次函數進一步研究發現,可以使用平移與縮放的方法把非標準二次函數轉化為標準二次函數或者亞標準函數,轉化前后其混沌特性是不變的,即其迭代序列的震蕩特性是相同的.另外,一個滿射函數和單位區域內標準函數復合后仍然是單位區域內標準函數,這樣,就可以把所有的二次函數變換到單位區域中進行研究,研究范圍可以縮小到單位區域中來.單位區域內的標準函數是重要的,既是研究混沌的本質,也是研究混沌化的方法,文獻[18—20]就是研究混沌化方法,并利用混沌化的方法產生序列進行圖像加密等,所以該類問題有必要深入研究.
本文工作是文獻[16,17]中研究工作的繼續,是在曲線研究的基礎上繼續研究單位區域內曲面的混沌特性.
2 使用雙二次有理貝賽爾曲面構造函數
鑒于函數圖像的幾何形狀與混沌特性有直接關系,又因為有理貝賽爾曲面的控制點可以調整曲面的形狀,所以使用有理貝賽爾參數曲面來研究曲面函數的混沌特性.作為有理貝賽爾曲面的一個特例,雙二次有理貝塞爾曲面定義如下:
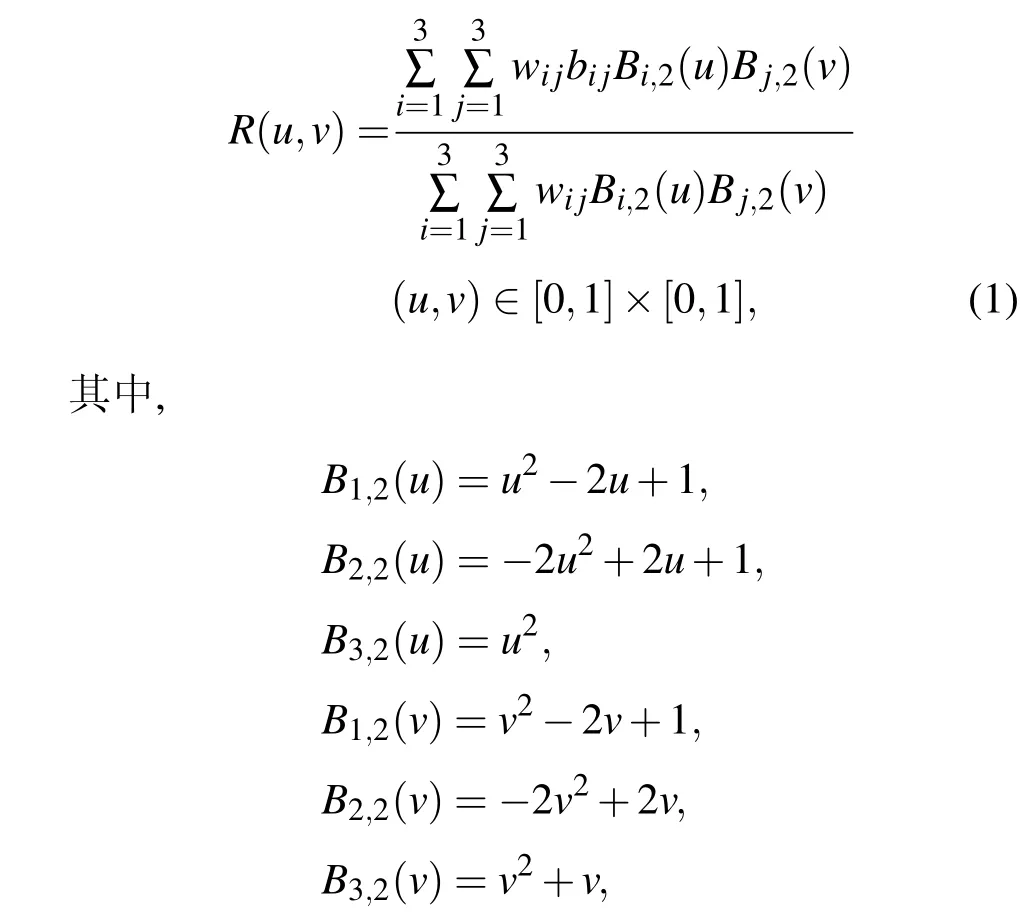
wi,j是權值,用來決定曲面的細節形狀(例如,這些參數可以確定該曲面的截面是拋物線、橢圓或者雙曲線等);bi,j是控制點,用來決定曲面主體結構形狀;雙二次有理貝塞爾曲面的變量x,y,z中的每個變量都需要9個控制點,然后由x,y,z構成空間曲面,是不超過4次的曲面.
在迭代過程中,如果使用x,y,z表示曲面,把u,v用x,y表示難度比較大,不易于實現迭代操作,所以在本文中直接使用u,v作為自變量進行研究.研究用的迭代表達式為
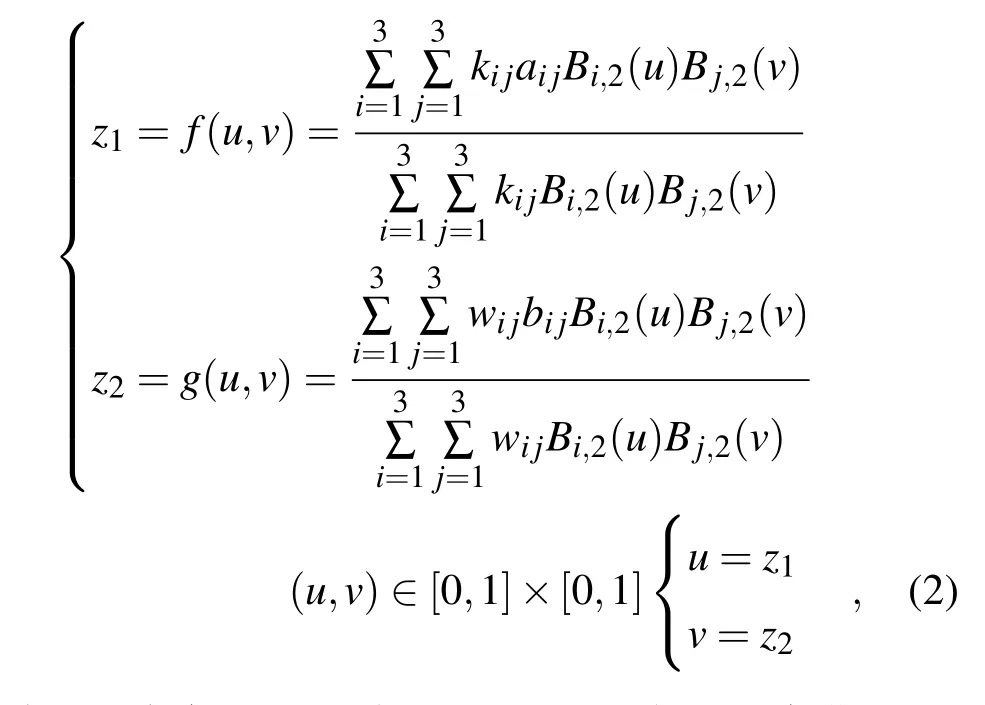
在(2)式中,f(u,v)與g(u,v)分別表示兩個曲面,u,v為自變量,定義域為[0,1]×[0,1],根據有理貝塞爾曲面的定義,當9個控制點為(0,0,0),(0,0.5,0),(0,1,0),(0.5,0,0),(0.5,0.5,m),(1,0,0),(1,0.5,0),(1,1,0)時,曲面的形狀如圖1(b)所示,四條邊界都在坐標軸上,圖形向上凸起,最大值為1.其中
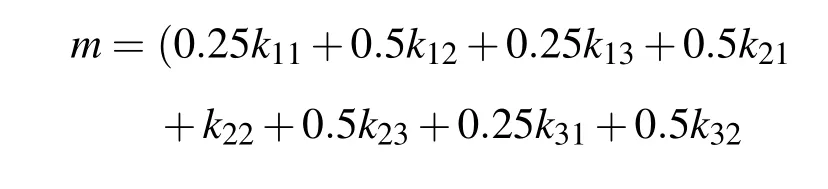
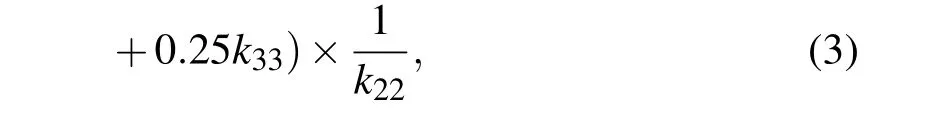
我們稱這種曲面為單位區域內的標準雙二次有理貝塞爾曲面.
研究發現,當(2)式中的兩個曲面有一個是標準雙二次有理貝塞爾曲面,另外一個曲面限制在單位區域內,迭代式(2)極易出現混沌.下面對這類曲面函數迭代進行研究.
3 單位區域內標準雙二次有理貝塞爾曲面迭代研究
隨機產生參數 kij與 wij,i=1,2,···,9,j=1,2,···,9,利用(3)式計算m,構造一個單位區域內的標準雙二次有理貝塞爾曲面;然后隨機生成控制點bij,i=1,2,···,9,j=1,2,···,9,構造另外一個二次曲面,兩個二次曲面構成迭代表達式.利用該表達式進行迭代,平均每迭代7,8次就可以出現一個混沌,說明在單位區域的有理數中,混沌的參數要占七分之一或者八分之一,這一數據是巨大的.
下面選擇有代表性的三個進行研究.
隨機生成的第一個曲面的權值參數以及第二個函數曲面參數如下:
迭代表達式(1)的參數

迭代表達式(2)的參數

迭代表達式(3)的參數


這些參數對應的圖形以及迭代后的吸引子圖形如圖1—3所示.
圖1到圖3在迭代的過程中,都是從u=0.3,v=0.6開始的,那么如果從其他的u,v開始迭代,是否也會出現類似的(近似)吸引子圖形呢?讓u與v都從0.01開始,迭代到0.99,步長為0.01,嵌套循環;對于每個u,v,迭代600次,去掉前100次,繪制后500次得到的點,結果繪制出的(近似)吸引子圖形如圖4所示,其形狀與圖1至圖3基本相同.這也說明了吸引子是不與初始迭代值有關的.
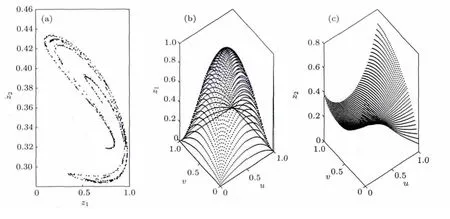
圖1 迭代表達式(1)的曲面與吸引子 (a)吸引子;(b)標準曲面;(c)隨機生成的曲面
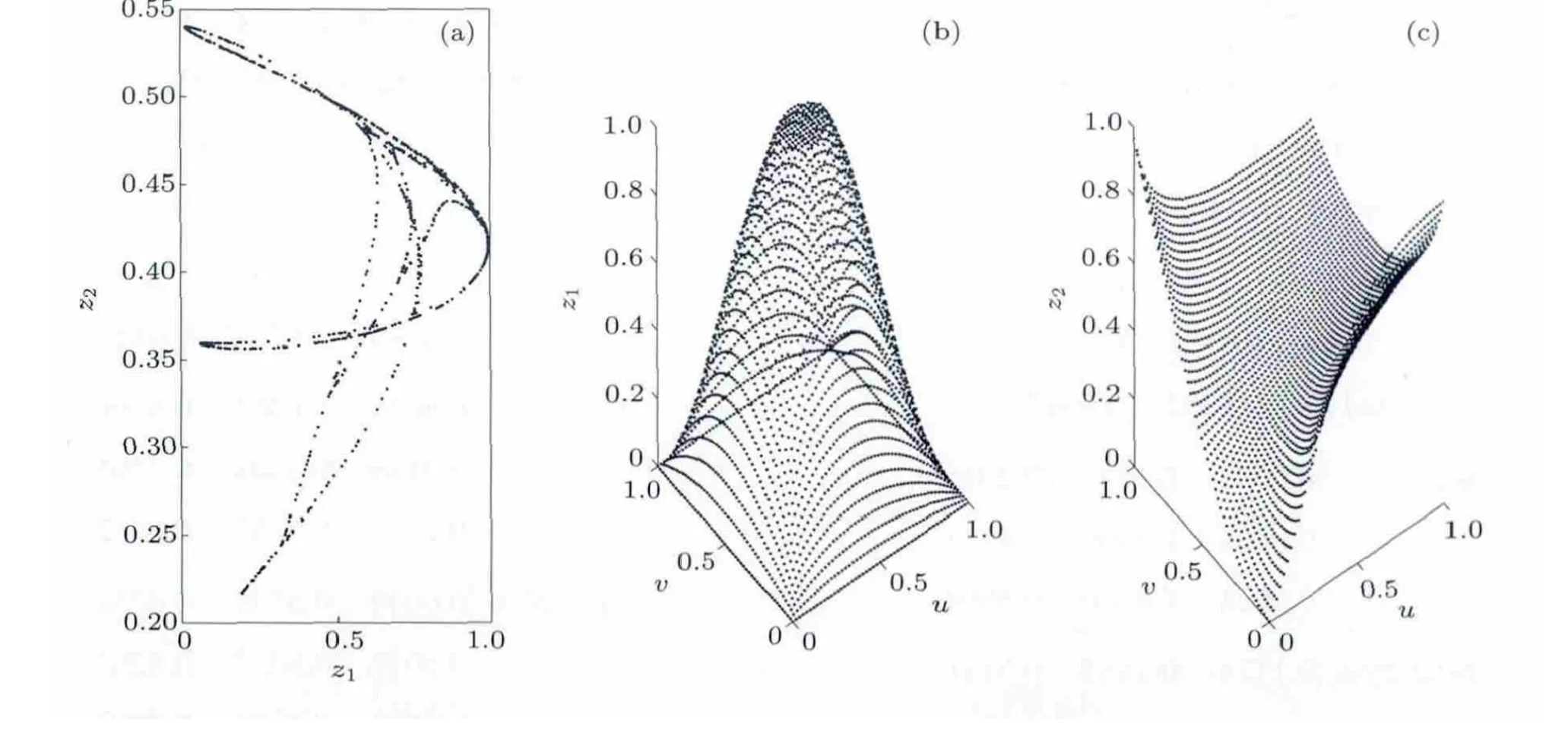
圖2 迭代表達式(2)的曲面與吸引子 (a)吸引子;(b)標準曲面;(c)隨機生成的曲面
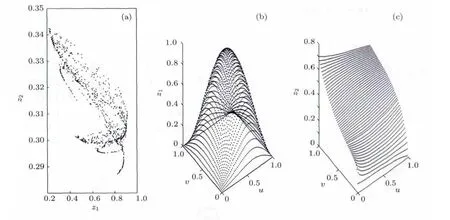
圖3 迭代表達式(3)的曲面與吸引子 (a)吸引子;(b)標準曲面;(c)隨機生成的曲面
為了更好研究上面迭代式的混沌特性,進一步繪制并觀察其分岔圖,如圖5是迭代式(2)當w(2,3)變化時的分岔圖.
通過大量的實驗觀察,第一個迭代表達式關于k和w的分岔圖都有一定的混沌區間,如表1所示.當其他參數不變的情況下,k(1,1)在1.5到4之間變化時,分岔圖呈現出混沌狀態;其他參數不變的情況下,w(1,1)在-1到0之間變化時,分岔圖呈現出混沌狀態.

表1 迭代表達式(1)的參數分岔區間
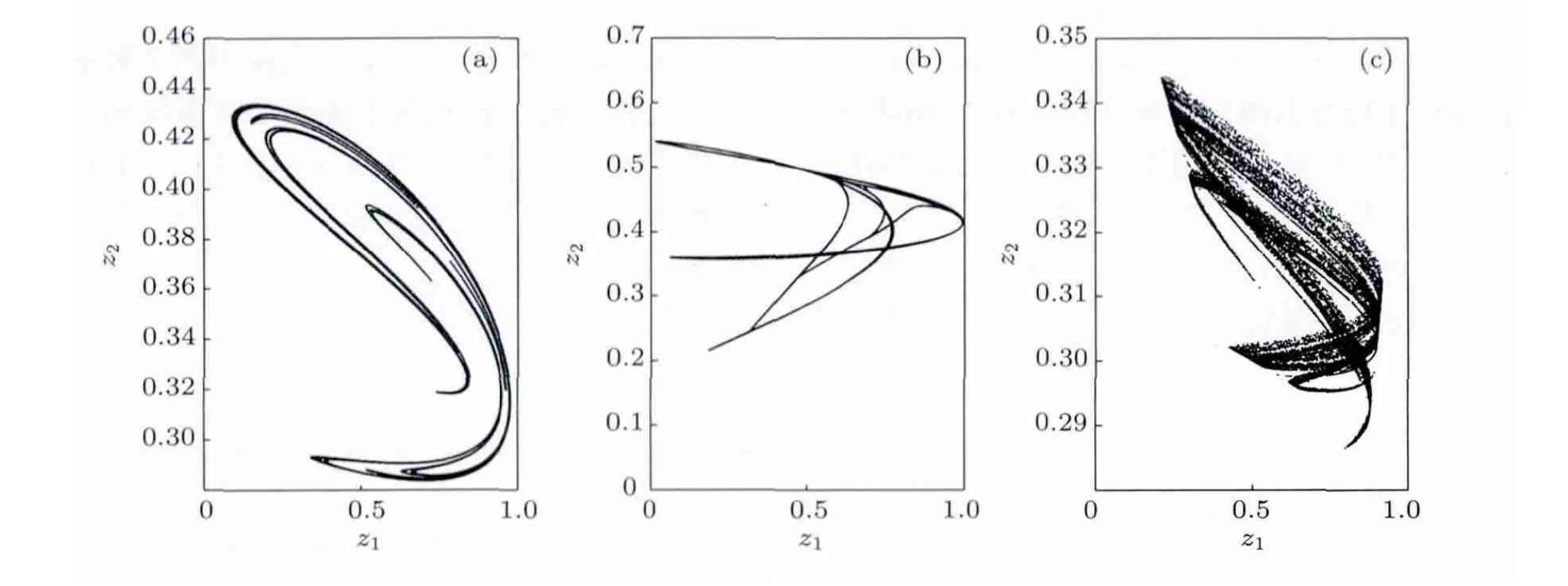
圖4 多個u,v繪制的吸引子 (a)迭代表達式(1);(b)迭代表達式(2);(c)迭代表達式(3)
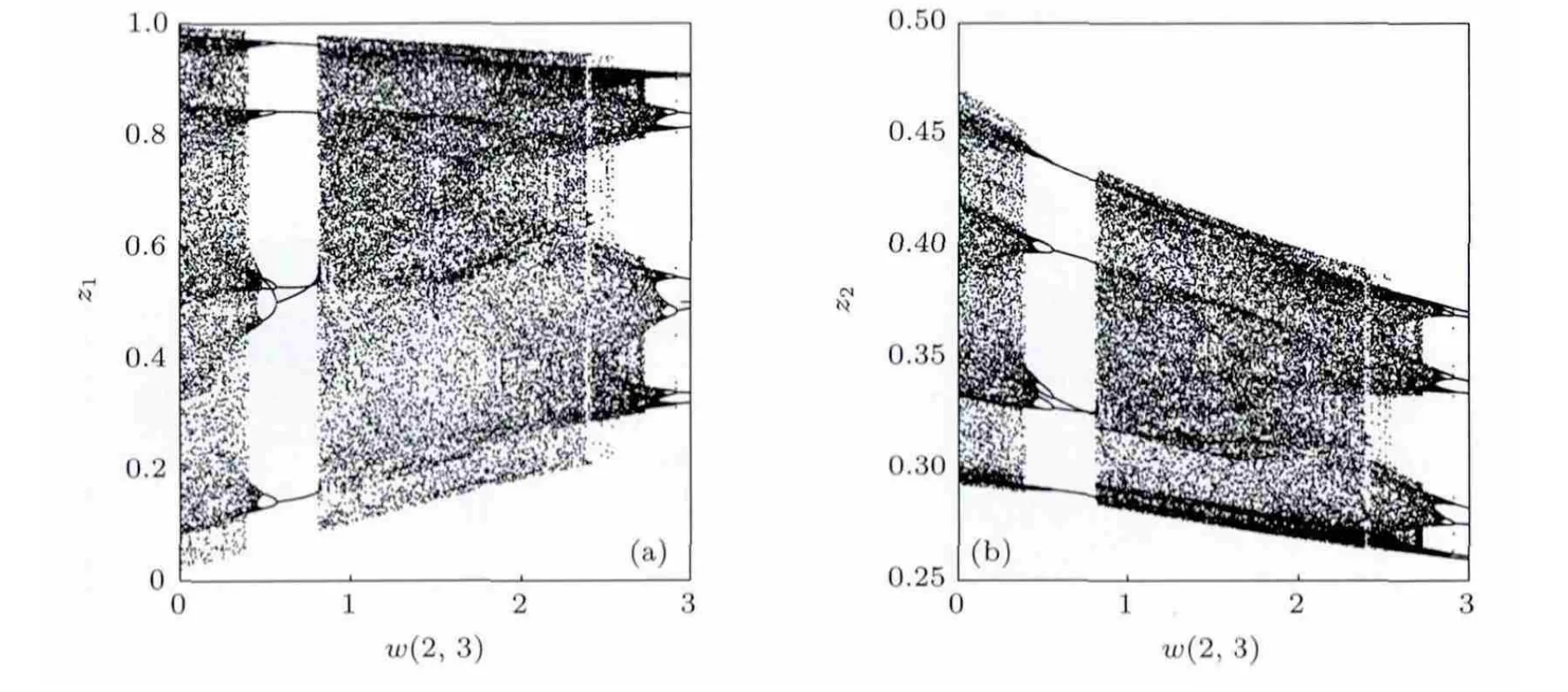
圖5 迭代式(1)當w(2,3)變化時的分岔圖 (a)z1分岔圖;(b)z2分岔圖
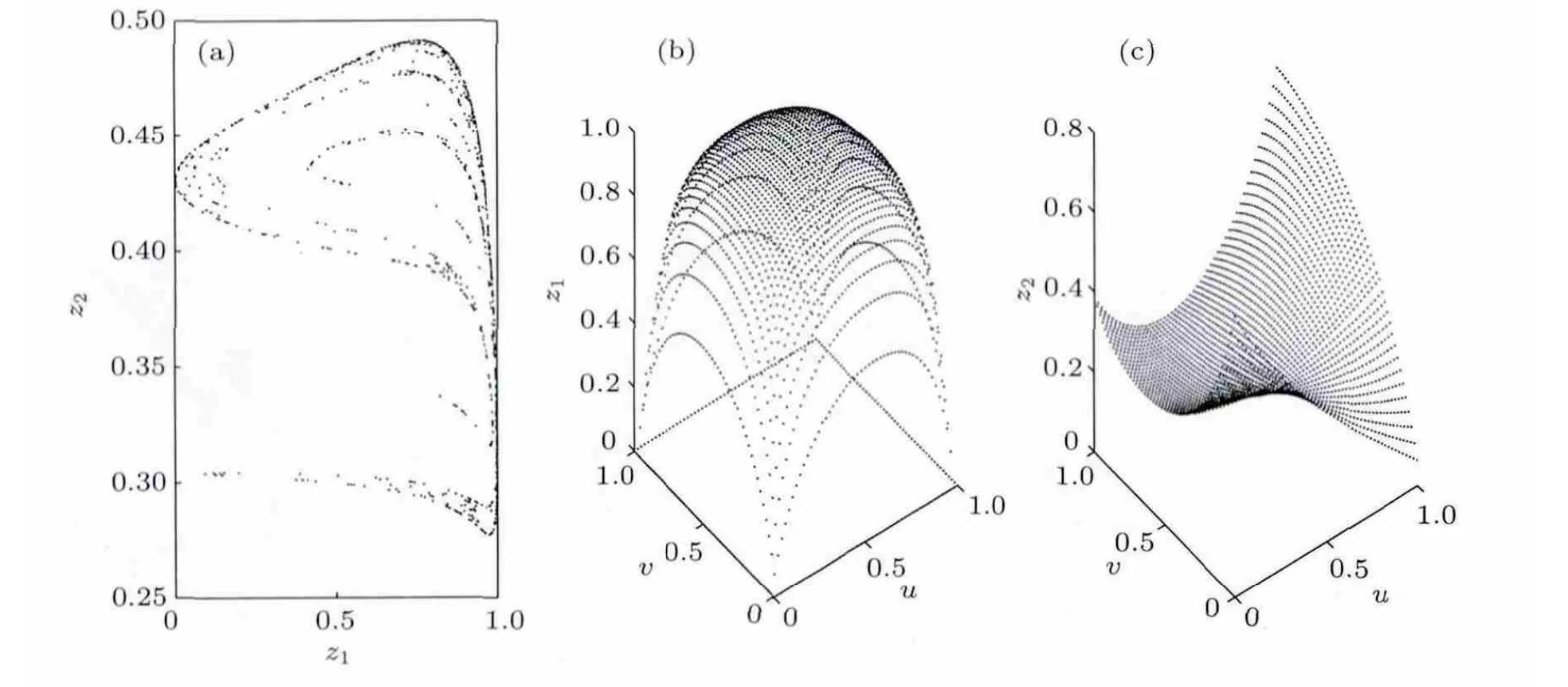
圖6 迭代曲面與吸引子(迭代式(1)參數k(2,2)變為10)(a)吸引子;(b)標準曲面;(c)隨機生成的曲面
利用表1,可以得到更多的混沌表達式,例如k(2,2)=10時,迭代表達式(1)其他參數不變,繪制出的吸引子以及其函數圖形如圖6所示,函數圖形與圖1(b)相比,函數圖形上部變平了而下部變陡;與圖1(a)相比,吸引子形狀也有改變.
迭代表達式(2)的參數分岔區間如表2所示.
從分岔圖的形狀上看,迭代表達式(2)的分岔圖與迭代表達式(1)的分岔圖有些區別,當w(2,3)變化時迭代表達式(2)的分岔圖如圖7所示.
利用表2,根據分岔圖上的混沌區間可以構造出很多新的分形圖,例如當w(2,3)=-0.3,其他參數不變時,繪制出的曲面圖以及吸引子圖形如圖8所示.

表2 迭代表達式(2)的參數分岔區間
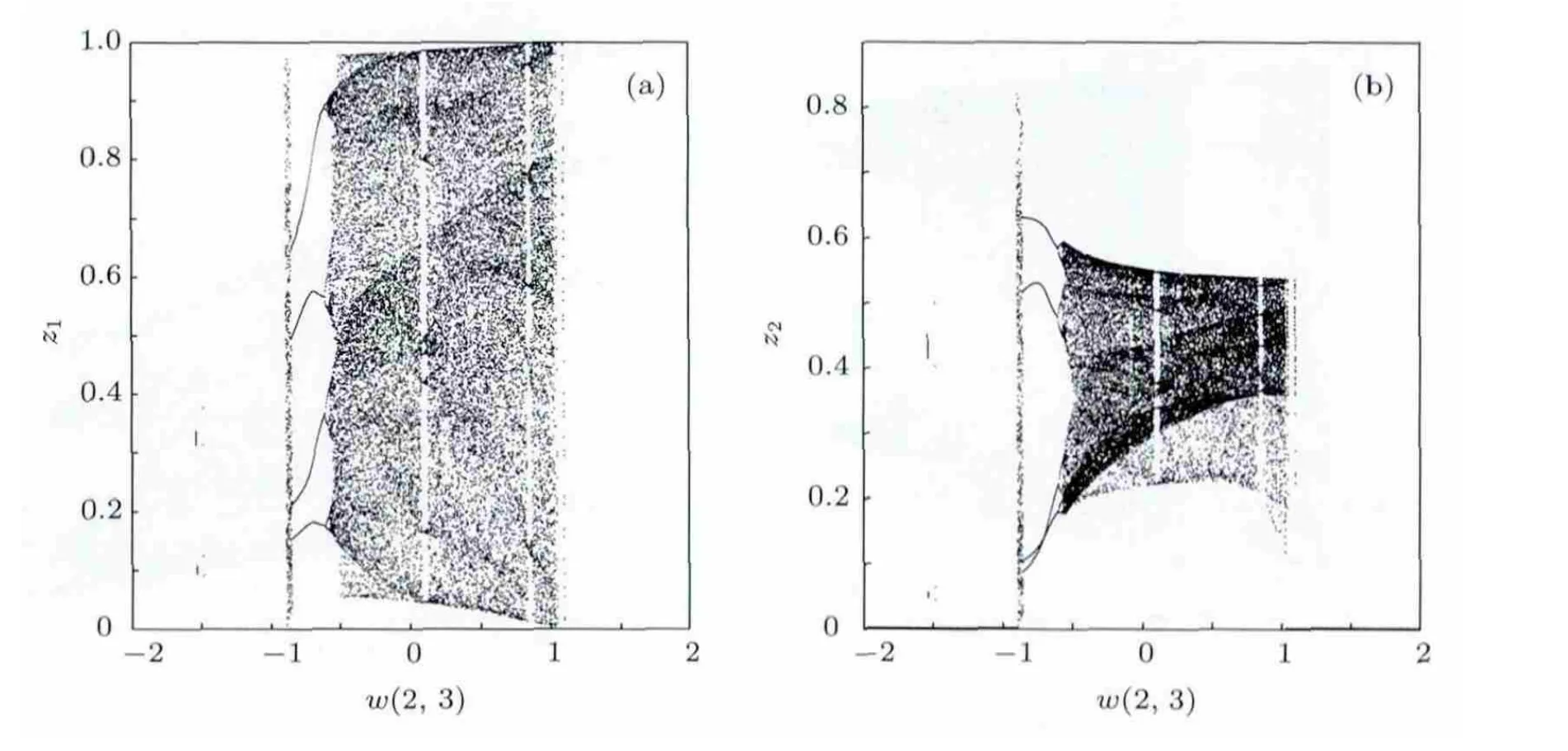
圖7 迭代式(2)當w(2,3)變化時的分岔圖 (a)z1分岔圖;(b)z2分岔圖

圖8 w2(2,3)=-0.3,其他參數不變時繪制的吸引子圖 (a)吸引子;(b)標準曲面;(c)隨機生成的曲面
為了研究多個參數同時變化時迭代式的混沌特性,繪制了二維分岔圖.圖9是迭代表達式(1)的一個二維分岔圖,圖10是迭代表達式(3)的一個二維分岔圖.

圖9 迭代表達式(2)的二維分岔圖(w2(2,3)w2(2,1)從0到10,步長0.2,迭代的初始值u=0.5;v=0.3)(a)z1關于w(2,1)w(2,3)的分岔圖;(b)z2關于w(2,1)w(2,3)的分岔圖;(c)w2(2,3)關于z1,z2的分岔圖
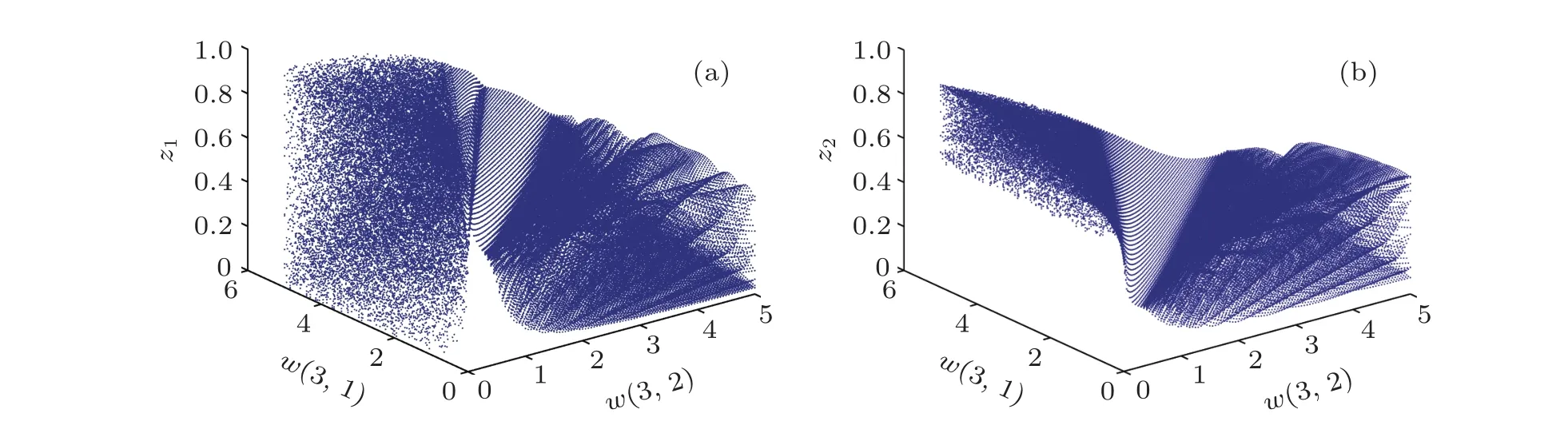
圖10 迭代表達式(3)的二維分岔圖(w2(3,1)w2(3,2)從0到5,步長0.1,迭代的初始值u=0.5;v=0.3)(a)z1關于w(3,1)w(3,2)的分岔圖;(b)z2關于w(3,1)w(3,2)的分岔圖
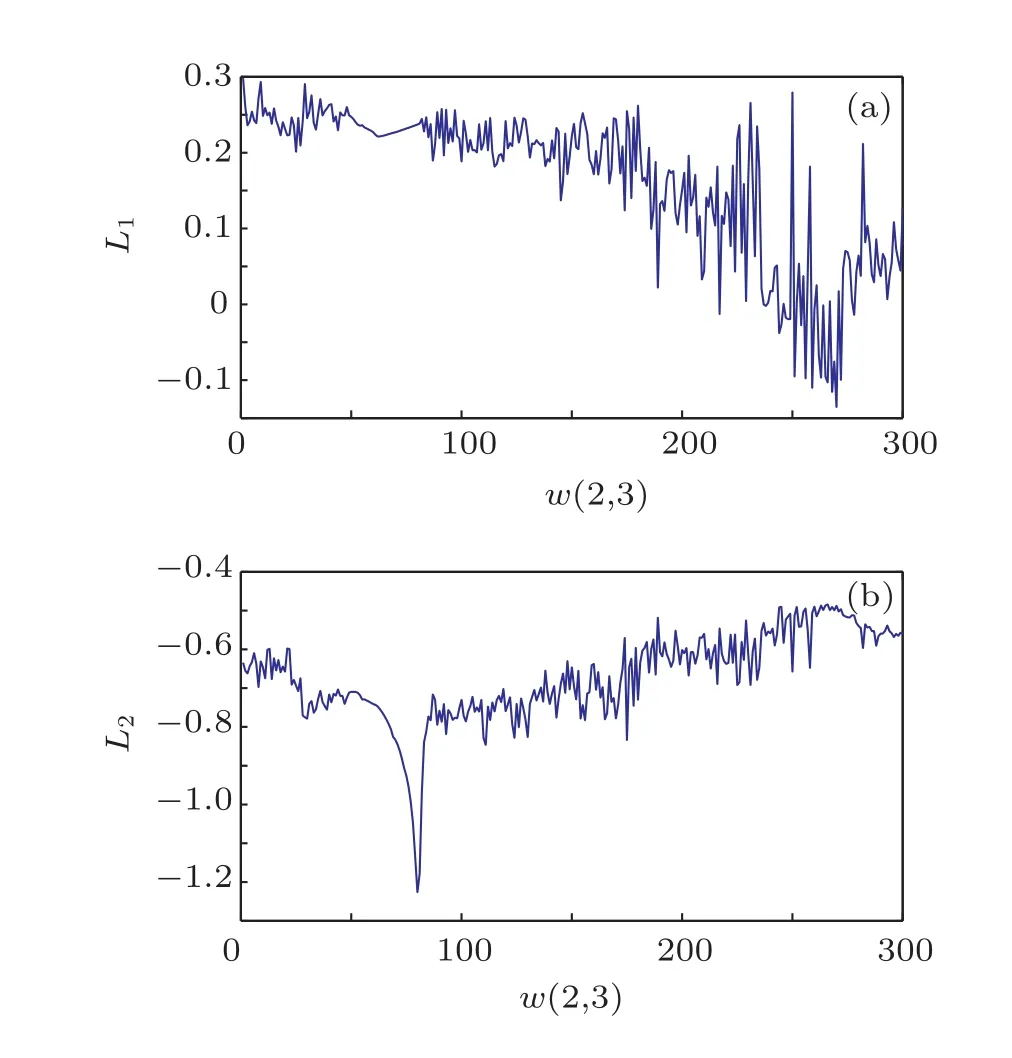
圖11 迭代表達式(1)的w2(2,3)變化時的Lyapunov指數圖,步長0.01;L1是z1的Lyapunov指數,L2是z2的Lyapunov指數
圖11是迭代表達式(1)的一個參數變化時的Lyapunov指數曲線圖,從該圖可以看出其Lyapunov指數為正數的區間.
4 單位區域上雙二次有理貝賽爾曲面迭代分析
兩個曲面構成一個二維迭代表達式,曲面的形狀決定了其是否是混沌的.在第3節中研究的幾個曲面都是固定第一個曲面的基本形狀,使得其在單位正方形的邊界處函數值都是0,中間凸起,最大值為1;第二個曲面是隨機生成的.事實上,之所以這種構造方法增大了混沌的概率,是因為第一個曲面的形狀與第2個曲面的形狀的差異性,在迭代的過程中易于出現混沌.圖12所示是迭代式(3)迭代后的函數圖像.例如,迭代2次就變成了z1=f(f(u,v),g(u,v))與z2=g(f(u,v),g(u,v)),如此類推,最后出現混沌.
當兩個曲面形狀相近時,不容易出現混沌狀況,圖13所示是一個沒有出現混沌的迭代.從圖13可以看出,隨著迭代次數的增加,z1和z2已經逐漸收斂.
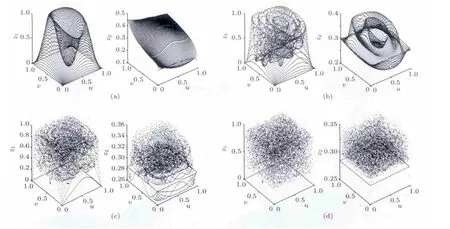
圖12 迭代表達式(3)多次迭代之后的曲面圖形 (a)迭代2次;(b)迭代4次;(c)迭代8次;(d)迭代16次
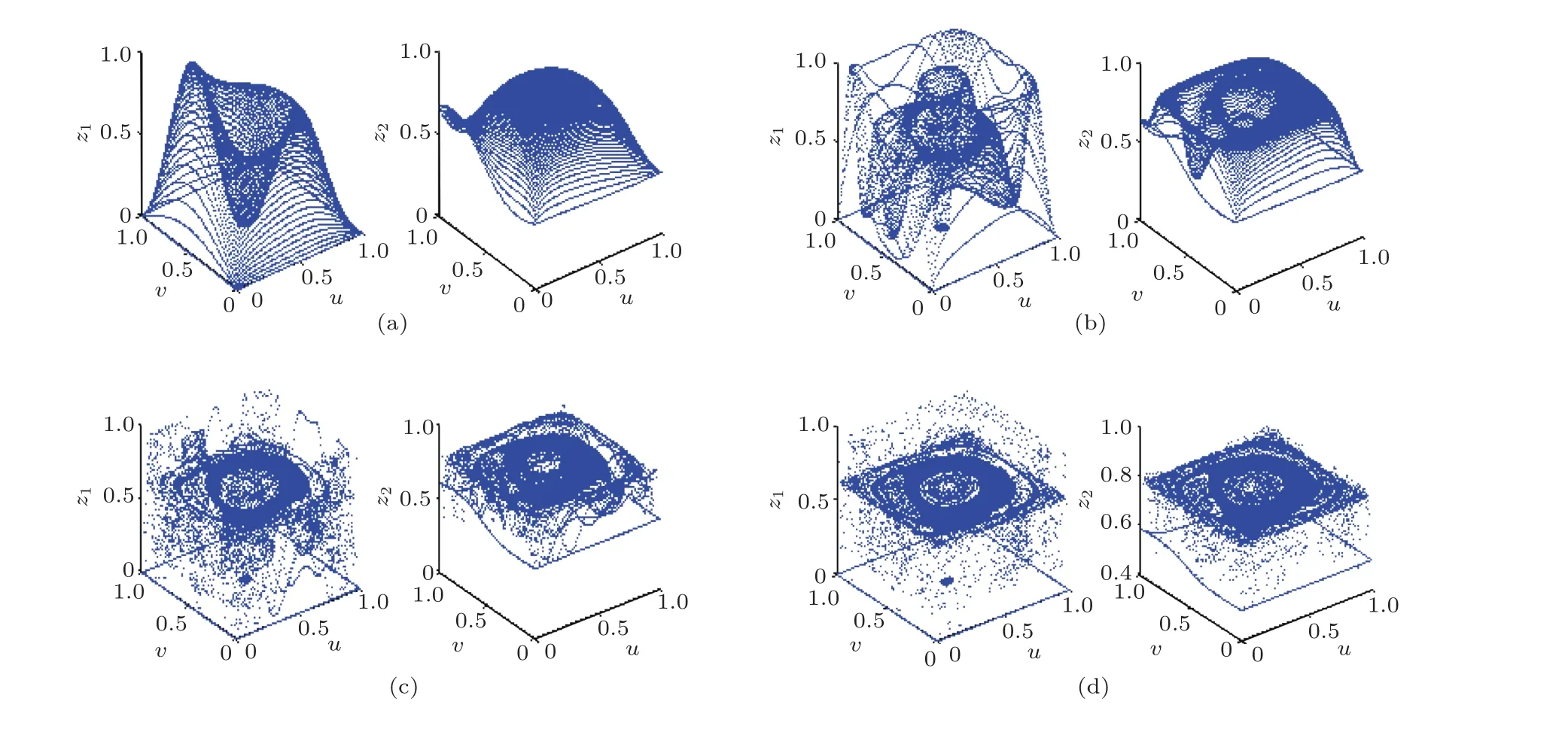
圖13 一個收斂的迭代表達式多次迭代之后的曲面圖形 (a)迭代2次;(b)迭代4次;(c)迭代8次;(d)迭代16次
從大量的實驗結果看,構成迭代表達式的兩個曲面形狀相近就不易出現混沌,很容易收斂;兩個曲面呈現對稱或者近似對稱,也不會出現混沌;一般當迭代出現混沌時,另外一個非標準函數曲面覆蓋區域越大,混沌的區間也越大.
5 圖像作為離散曲面的混沌特性研究
圖像本質上是一個離散的函數,調整圖像,可以構造出混沌映射.基本的構造方法是把圖像調整到長寬以及顏色值一樣,本文是都調整到1到256,這樣就可以讓圖像的下標與圖像的顏色值進行交換,以便實現類似離散動力系統的迭代.
圖14中顯示了把大小為480×640的兩個圖像調整為256×256大小,并且把彩色圖像也變為灰度圖像.
下面以一個簡單的迭代為例對圖像迭代進行研究.
迭代從x1=23,y1=109開始,圖14(b)在(23,109)的灰度值為144,圖14(d)在(23,109)的灰度值為255;取出144,255這兩個顏色值,然后把(144,255)作為下標,到圖14(b)中去查找像素(144,255)位置的灰度值,灰度值為75,再到圖14(d)中去查找像素(144,255)位置的灰度值,灰度值為118;然后再以(75,118)為下標,繼續迭代取值,如此下去.迭代的序列如下所示:

在12次內還沒有重復,也就是還沒有陷入到周期點中;編寫程序,計算得到該迭代次數小于50000次時,沒有出現過第二個(23,109),也就是(23,109)的周期要大于50000.

圖14 把圖像調整到256×256大小 (a)圖像1原;(b)圖像1調整后圖;(c)圖像2原圖;(d)圖像2調整后
改變初始值進行迭代,計算出當迭代起始點為x1=77,y1=124時,迭代到236次的時候,出現重復,也就是第236次后,其下標也是x1=77,y1=124,所以可以說(77,124)是236階周期點.進一步實驗得到(76,124)也是236階周期點,但是(75,124)與(78,124)迭代50000次還不曾重復.迭代50000次不重復的點很多,例如,x1=7,y1=12時,迭代72500次也沒有出現重復.
下面研究究竟哪些點周期小,哪些點周期大.共迭代25000次,把在25000次迭代之內重復的繪制出來,如圖15所示.從圖15看,重復的還是少數點.
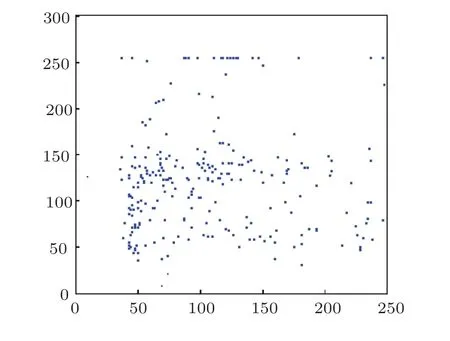
圖15 小于25000的周期點分布示意圖
上面研究的是一種最簡單的圖像迭代,可表示為
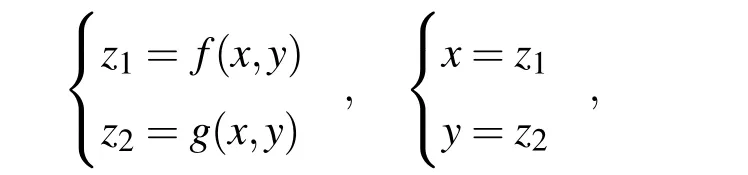
其中 f(x,y)與g(x,y)表示兩幅灰度圖像.
實驗結果還表明,有大量的圖像經過這樣組對迭代后很容易收斂,得到的基本結論是同一物體的不同圖像放在一起進行迭代易于收斂,不同的或者不相近的圖像放在一起不易于收斂,所以初步判斷改進該方法可以用于圖像識別與跟蹤、圖像理解、圖像數據庫構造等.
6 總結與展望
本文研究了單位區域內雙二次貝賽爾曲面構成的函數的混沌特性,研究發現把其中一個曲面調整為標準曲面,極大地增加了該函數的混沌概率.隨機生成兩個曲面,構造迭代使混沌的概率不到千分之一,使用本文方法可以使得混沌的概率大于百分之十.在大量的混沌函數中選擇三組函數進行了詳細研究,通過分岔圖以及Lyapunov指數曲線圖觀察函數的混沌特性.利用這些分岔圖可以得到更多的參數,這些參數能夠構造出混沌函數.這是一個構造混沌、發現混沌的較好的實用的方法.
進一步的工作需深入研究雙二次貝賽爾曲面構成的函數的混沌特性,給出一些結論性的結果,并給出說明或者證明;研究三個三元迭代式在單位區域中的混沌特性,例如把洛倫茲系統族當作一個特例進行研究,研究調整其形狀后什么情形下出現混沌;另外,依據現有的混沌理論與實驗結果,繼續研究圖像迭代的混沌特性,期待發現新的結果,例如把一個圖像和一個標準函數放到一起迭代,關于這個內容,從最近作者研究結果看,可以作為一種圖像識別的方法;事實上,也可以利用單位區域函數的作用研究較規范的湍流問題,如圓柱形管道中的管內的流體的受力、加速度或者速度等可以用標準函數或者亞標準函數來表示,這樣可以更好地利用混沌研究湍流問題.
[1]Li T Y,York J A 1975 Am.Math.Monthly 82984
[2]Chen X F,Chen G,Yu X 2000 Chaos Soliton.Fract.10771
[3]Chen Y C 2008 Int.J.Bifurc.Chaos 181825
[4]Liu H,Wang L D,Chu Z Y 2009 Nonlinear Anal.716144
[5]Akhmet M U 2009 Math.Anal.Appl.351804
[6]MengJD,BaoBC,XuQ2011ActaPhys.Sin.60010504(inChinese)[孟繼德,包佰成,徐強2011物理學報60010504]
[7]Zhang Y S,Xiao D,Shu Y L,Li J 2013 Signal Process-Image 28292
[8]Liu S X,Guan H Z,Yan H 2012 Acta Phys.Sin.61090506(in Chinese)[劉詩序,關宏志,嚴海2012物理學報61090506]
[9]Shi Y M,Chen G 2005 Int.J.Bifurc.Chaos 15547
[10]Shu Y L 2008 Nonlinear Anal.691768
[11]Aghababa M P 2012 Chin.Phys.B 21100505
[12]Sun C C,Xu Q C,Sui Y 2013 Chin.Phys.B 22030507
[13]Jiang G R,Xu B G,Yang Q G 2009 Chin.Phys.B 185235
[14]Zhao Y,Zhang H G,Zheng C D 2008 Chin.Phys.B 170520
[15]Liu N,Guan Z H 2009 Chin.Phys.B 181769
[16]Yu W B,Wei X P 2006 Acta Phys.Sin.553969(in Chinese)[于萬波,魏小鵬2006物理學報553969]
[17]Yu W B,Yang L Z 2013 Acta Phys.Sin.62020503(in Chinese)[于萬波,楊靈芝2013物理學報62020503]
[18]Yu W B,Yang X S,Wei X P 2011 Appl.Res.Comput.283837(in Chinese)[于萬波,楊雪松,魏小鵬2011計算機應用研究283837]
[19]Yu W B,Yang L Z 2013 Comput.Engineer.395(in Chinese)[于萬波,楊靈芝2013計算機工程395]
[20]Xu Z G,Tian Q,Tian L 2013 Acta Phys.Sin.62120501(in Chinese)[徐正光,田清,田立2013物理學報62120501]

