Dijkstra 最短路徑算法的優化及在應急交通中的應用

姜惠娟

(定西師范高等專科學校 計算機系，甘肅 定西 743000)

1 問題的提出

隨著城市規模的快速發展，城市交通也越來越復雜，在緊急救援物資運輸、醫療急救、110 報警、火警等應急交通中一般要求能在盡可能短的時間內找到到達目標地的最佳路線，而且在行車途中通常需要實時計算車輛前方的路線、路況，這就要求能計算任意兩個節點間的最短路徑，而且問題的解決是高效的.而傳統的Dijkstra 算法解決的是從一定點到其他各節點的最短路徑，且計算時間長、所需存儲空間大.筆者在分析Dijkstra 算法特征的基礎上，從兩個方面對算法進行改進.將改進后的算法應用于應急交通系統中搜索最佳路徑，實踐證明，該方法提高了效率.

我們通常所說的最短路徑不僅指距離最短，還可以指時間最短、費用最小、線路容量最小等.相應地，最短路徑問題就成為最快路徑問題、最低費用等問題，即:最優路徑問題實質是求加權圖G=＜V、E、W ＞中給定兩點間的最短路徑，而迪克斯特拉(Dijkstra)算法就是求最短路徑的著名算法之一［1］.

2 Dijkstra 最短路徑算法分析

2.1 算法描述

帶權有向圖用G=＜V，E ＞表示，其中V 是頂點集，E 是邊的集合，該算法的核心是按照路徑長度遞增的次序產生最短路徑.圖中的頂點集合V 分成兩組，用M 表示已求出最短路徑的頂點集合，用N 表示尚未確定最短路徑的頂點集合，用數組T［N］表示某步中從vi到vk的最短路徑.算法核心步驟可歸納為:

(1)初始時，M={vi}，N=V－{vi}，如果vi到vk有弧，T［k］等于該弧上的權值;如果無弧存在，則T［k］等于無窮大;

(2)從N 中找T［k］最小的vk加入M，并將其從N 中刪除，若N 為空，算法結束，否則進行步驟(3);

(3)將k 結點與N 中其他結點比較，若T［j］＞T［k］+arcs［k］［j］(弧＜vj，vk＞上的權值)，那么用T［k］+arcs［k］［j］代替原來的T［j］，重復步驟(2);

(4)算法結束，這時T［k］中存放的即為從vi到vj的最短路徑.

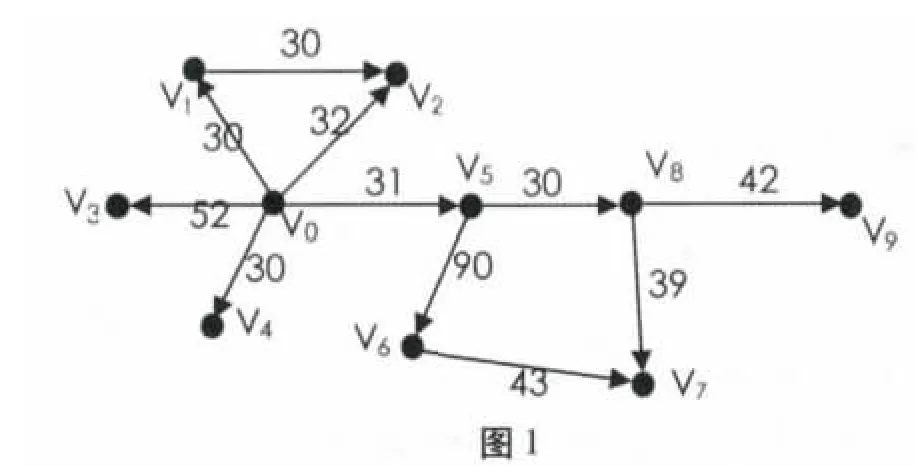
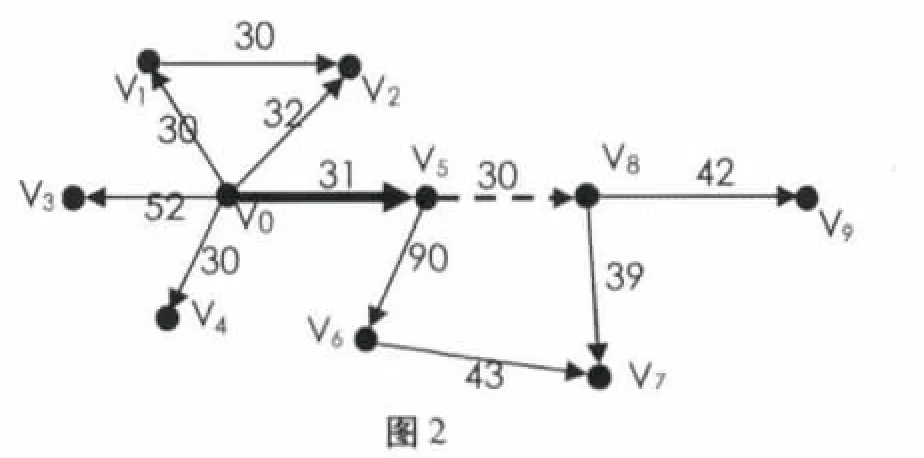
某地區部分交通線路圖如圖1 所示，采用Dijkstra 算法尋找從v0到v7的最短路徑，圖2 中加粗部分表示已經找到的最短路徑.對于已經找到的每條路徑長加上相鄰頂點和已知路徑中相應頂點間的距離和作比較，選出最接近起點vo的下一條頂點v8，然后將弧＜v5，v8＞加入到已知的最短路徑中，采用同樣的方法循環，直到查找到所有的最短路徑.

2.2 算法時間效率分析

首先，Dijkstra 算法產生的是一棵以源點v0為根的樹，算法執行則該樹向四周延伸，其中有些分支對求最短路徑是沒有幫助的;其次，算法的每次循環就是從待處理的節點集合N 中取距離最小的一個節點加入M 中，使最優路徑擴大一個節點，從而保證一步最優，但整體效果并未最優［2］.

Dijkstra 算法本身時間復雜度為Ο(n2)，如果要求任意兩個結點間的最短路徑，則需要重復執行Dijkstra 算法n 次［3］，所以總的時間復雜度為Ο(n3).當網絡節點數n 增大時，計算時間會成倍或冪次增大.因此，在交通線路非常復雜的情況下，該算法運算時間長、求解效率低，很難滿足應急交通系統的實際要求.

3 優化Dijkstra 最短路徑算法

3.1 根據圖節點的出、入度優化算法

3.1.1 根據節點的出度優化算法

優化思想:若結點vi的出度為1，則它只有唯一的后繼節點vj，那么vi到vj的最短路徑即為弧＜vi，vj＞上的權值［3］;vi到其他各結點的最短路徑就等于vj到其他各結點的最短路徑加上弧＜vi，vj＞上的權值即可.

根據以上思想，優化后算法的具體步驟可以總結如下:

(1)計算所有結點的出度;

(2)將出度為1 的結點用si表示;

(3)如果一個節點的出度為1，則不必求從此結點出發的最短路徑，先求其后繼結點到其他節點的最短路徑，在此基礎上加上si節點的唯一出度邊的權值則可得到從該si節點出發到其他節點的最短路徑;

(4)重復步驟(2)、(3)，直到沒有出度為1 的結點.

如圖1 中，結點v1、v6的出度為1，v1的唯一后繼結點為v2，v6的唯一后繼結點為v7，因此不必先求這兩點到其他結點的最短路徑，只需先求出v2、v7結點到其他結點的最短路徑，v1到其他結點的最短路徑即為v2到相應結點的最短路徑加上弧＜v1，v2＞上的權值;v6到其他結點的最短路徑即為v7到相應結點的最短路徑加上弧＜v1，v2＞上的權值.

3.1.2 根據節點的入度優化算法

優化思想:如果某結點的入度為0，則其他結點到該結點均不可到達，因此其他節點到該節點的最短路徑均為無窮大，而且該節點不會出現在其他任意兩個結點間的最短路徑上，所以在計算其他各結點間的最短路徑時，可以將入度為0 的結點先刪除.根據此優化思路，以下是優化后算法的具體步驟:

(1)計算各結點的入度;

(2)將入度為0 的結點用vi表示;

(3)采用Dijkstra 算法計算從vi到其他各結點的最短路徑;

(4)求完最短路徑后如果結點vi的入度為0，則將該結點從圖中刪除，以簡化有向圖，從而簡化了后面的計算過程;

(5)重復步驟(2)、(3)，直到沒有入度為0 的節點.

如圖1 所示，v0的入度為0，當計算出以v0結點出發到其他各結點的最短路徑后，再計算其他結點間的最短路徑時，就可以將結點A 刪除，并把其他結點到v0結點的最短路徑標為無窮大.

通過算法優化，提前消減了圖中無益于求最短路徑的分支，提高了效率.

注意，不管是從入度還是從出度優化，都必須考慮出入度為1 的多個結點，而且要注意該節點的前驅結點的次序.

3.2 根據已知的最短路徑快速計算其他最短路徑

如果R，S，T 是從R 到T 的最短路徑，則R 到S 的最短路徑、S 到T 的最短路徑不必再采用Dijkstra算法去計算，而可以通過已經得到的R 到T 的最短路徑直接得到:R 到S 的最短路徑為R，S，S 到T 的最短路徑為S，T［4］.

證明:已知結點R 到結點T 的最短路徑為R，S，T;假設結點R 到結點S 的最短路徑不是R，S;而是R，…，S;那么可得出R，S，…，T;此路徑比路徑R，S，T 更短，這與已知條件R 到T 的最短路徑為R，S，T相矛盾.于是，得到R 到S 的最短路徑一定為R，S;同理可以得到S 到T 的最短路徑為S，T.

在圖3 中，如果O 到Q 的最短路徑已經算出為:O，P，S，Q，則直接可以得出O 到P 的最短路徑為:O，P;O 到S 的最短路徑為:O，P，S;P 到S 的最短路徑為:P，S;P 到Q 的最短路徑為:P，S，Q，而不需要再采用Dijkstra 算法去計算.

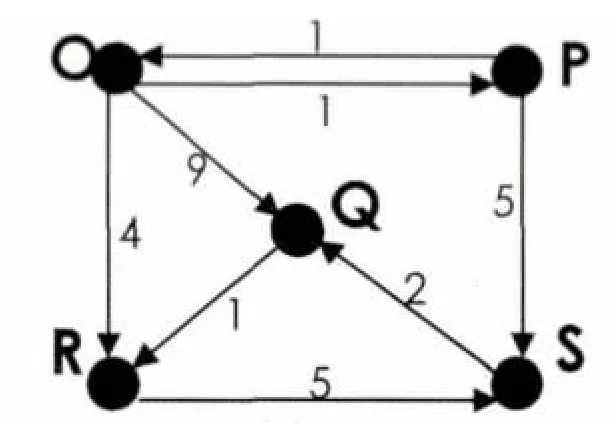
圖3

采用此優化策略對圖3 中任意兩結點快速計算最短路徑的具體步驟如下所示:

O 到Q 的最短路徑:O，P，S，Q——直接由Dijkstra 算法計算得到;

O 到P 的最短路徑:O，P——由已知最短路徑直接得到;*

O 到S 的最短路徑:O，P，S——由已知最短路徑直接得到;*

P 到S 的最短路徑:P，S——由已知最短路徑直接得到;*

P 到Q 的最短路徑:P，S，Q——由已知最短路徑直接得到;*

P 到R 的最短路徑:P，O，R——直接由Dijkstra 算法計算得到;

P 到O 的最短路徑:P，O——由已知最短路徑直接得到;*

O 到R 的最短路徑:O，R——由已知最短路徑直接得到;*

R 到Q 的最短路徑:R，S，Q——直接由Dijkstra 算法計算得到;

R 到S 的最短路徑:R，S——由已知最短路徑直接得到;*

S 到Q 的最短路徑:S，Q——由已知最短路徑直接得到;*

Q 到S 的最短路徑:Q，R，S——直接由Dijkstra 算法計算得到;

Q 到R 的最短路徑:Q，R——由已知最短路徑直接得到;*

R 到S 的最短路徑:R，S——由已知最短路徑直接得到;*

S 到R 的最短路徑:S，Q，R——直接由Dijkstra 算法計算得到;

S 到Q 的最短路徑:S，Q——由已知最短路徑直接得到;*

Q 到R 的最短路徑:Q，R——由已知最短路徑直接得到.*

從優化后的算法可以看出17 組結點間的最短路徑，只有末用星號標注的組是直接采用Dijkstra 算法計算到，其他均采用已經得到的最短路徑直接得出，最短路徑的查找效率提高了許多［5］.

4 小結

隨著最短路徑算法在人們實際生活中的應用越來越廣泛，研究高效的最短路徑算法很有價值.本文對Dijkstra 經典算法的執行過程分析后，針對該算法存在的計算時間長、效率低等問題，從節點的出、入度信息和全局最優化兩個角度對Dijkstra 算法進行優化，給出了算法的實現過程.實踐證明，將優化后的算法應用于應急交通系統中有效地減少了最短路徑的計算時間，提高了查找效率.

［1］嚴蔚敏，吳偉民.數據結構［M］.北京:清華大學出版社，2007.

［2］鄧春燕.兩種最短路徑算法比較［J］.電腦知識與技術，2008，15(12):511－513.

［3］田豐.圖與網絡流理論［M］.北京:科學出版社，1987.

［4］龍光正，楊建軍.改進的最短路算法［J］.系統工程與電子技術，2009，24(6):106－108.

［5］土曉東，陳國龍，林柏鋼.網絡最短路問題的改進算法［J］.小型微型計算機系統，2009，23(9):1083－1087.