分數階微分算子增強圖像邊緣和紋理

周昌雄，陶文林，尚 麗，顏廷秦，2，馬國軍

(1．蘇州市職業大學電子信息工程系，江蘇蘇州215104;2．蘇州市數字化設計與制造技術重點實驗室，江蘇蘇州215104;3．江蘇科技大學電子信息學院，江蘇鎮江212003)

1 引言

圖像是記錄和傳遞信息的重要載體和手段，由于多種原因，圖像在生成、傳輸和變換的過程中會產生質量下降和特征淹沒現象，對圖像分析和識別帶來困難［1－3］。因此，突出圖像中的有用信息，擴大圖像中不同物體特征之間的差別，從而改善圖像的視覺效果是圖像增強的目的。目前，人們提出了很多圖像增強的算法，如基于直方圖的增強和基于空域或頻域的增強等。采用基于空域的傳統整數階微分方法增強圖像的紋理信息，其微分結果約等于零，必然會使紋理細節大幅衰減，造成圖像的紋理細節和邊緣模糊不清［4－6］。因此，既要提升圖像邊緣又要加強紋理細節，成為圖像增強研究的熱點和難點問題。

分數階微分是整數階微分運算的推廣，通過對分數階微分的理論研究發現，在對信號進行分數階微分運算，當微分階次小于1時，既能大幅提升信號的高頻分量有能加強信號中的低頻分量，且對信號的甚低頻沒有進行大幅衰減。相較傳統的整數階微分圖像增強方法，分數階微分用于圖像增強處理將使圖像邊緣明顯增強、圖像紋理細節更加清晰并且非線性保留圖像平滑區域信息［7－8］。在文獻［4］中運用5×5窗口大小，對灰度圖像和彩色圖像采用不同分數階微分算子增強，實驗結果表明，當微分階次在0．4～0．6之間圖像的增強效果最好，圖像的邊緣信息和局部紋理細節被加強，當微分階次大于0．6以后圖像中的噪聲明顯被放大。在文獻［9］中，將5×5窗口分數階微分模板分解為八個不同方向的小模板，求得像素點周圍八個方向加權和的最大值作為該像素點的增強值。實驗表明，改進方法既增強圖像邊緣又豐富了圖像的紋理細節信息。圖像像素鄰域內像素點的灰度值具有關聯性，分數階微分算子模板窗口越小，模板窗口內像素點的灰度值關聯性越大。本文提出將3×3模板窗口劃分成四個方向的小模板，求得中心像素點周圍四個方向加權和的最大值作為該中心像素點的增強值，據此增強圖像的邊緣信息和紋理細節信息能獲得較明顯效果。

2 分數階微分原理

2．1 分數階微分頻域性質

對于任意平方可積的能量信號s(t)∈L2(R)，設其Fourier變換為S(ω)，則ν階分數微分Dνs(t)的Fourier變換如下:

信號ν階分數微分Dν算子其特性函數為:

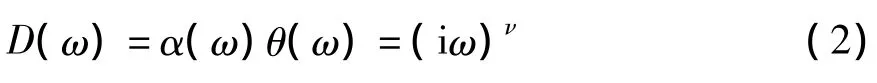
其中，α(ω)和θ(ω)分別為微分Dν算子的幅頻特性函數和相頻特性函數，其表達式如下:

在式(3)幅頻特性函數 α(ω)中，分別取 ν為0．1，0．5，0．8 和1，將 α(ω)數字化如圖1 所示。

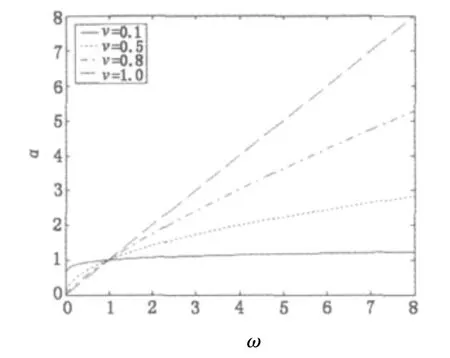
圖1 微分算子的幅頻特性曲線

從圖1中可以看出，微分運算有提升高頻信號的作用，并且隨頻率ω和微分階次ν的增加，幅頻特性曲線呈非線性增長。當ν=1為一階微分算子，利用一階微分算子處理圖像雖然能大幅增加圖像邊緣高頻成分，但是對圖像中灰度變化不大的紋理細節信息中低頻部分必然會大幅的線性衰減，其結果約等于零。當0＜ν＜1時，其特性曲線為分數階微分特性曲線，與ν=1的直線相比，分數階微分特性曲線在信號高頻成分增幅小于一階微分算子，而在信號的中頻和低頻成分增幅大于一階微分算子。因此，可利用分數階微分增強圖像的邊緣，同時增強圖像的紋理。

2．2 分數階微分定義與算子

分數階微分定義有多種，若信號s(t)∈［a，t］(a＜t，a∈R，t∈R)，當 ν＞0 時，信號s(t)非整型 ν階微分G－L定義表達式:

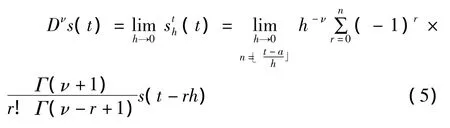
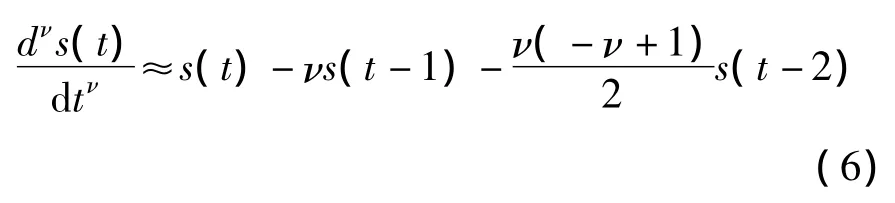
針對二維數字圖像f(x，y)，定義坐標軸(x，y)方向上分數階微分后向差分近似表達式分別為:

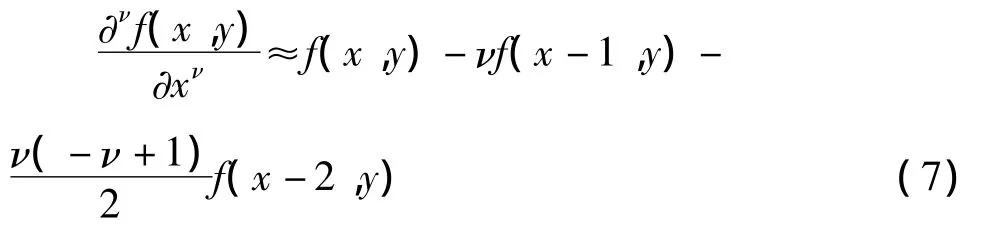
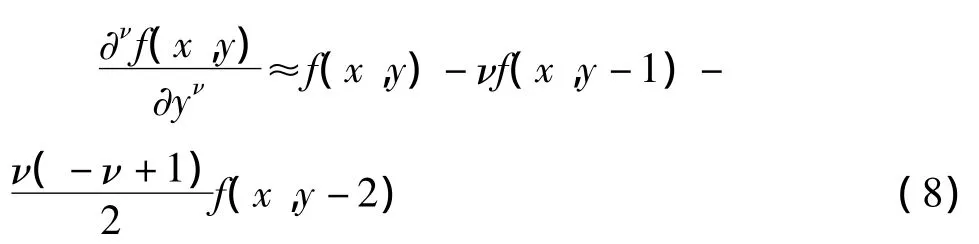
為了實現圖像增強，選擇分數階差分定義的前3項作為二階近似值，采用5×5模板:

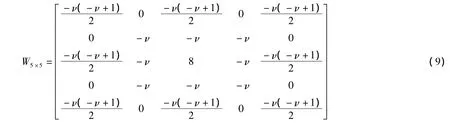
一般來說，對M×N的圖像f(x，y)增強，可用m×n大小的模板進行對其線性濾波，增強后的圖像g(x，y)表達為:

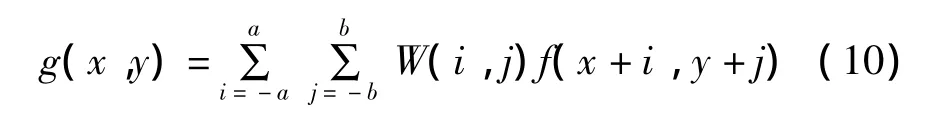
其中，a，b分別為分數階微分算子模板大小在x，y坐標軸方向上的半徑。

2．3 改進分數階微分算子

根據式(10)分數階算子增強圖像紋理和邊緣信息，為了使得增強的圖像亮度不發生較大變化，首先將增強算子歸一化，即W5×5的每項除以(8－12ν+4ν2)，然后用分數階算子增強算子對圖像進行卷積運算。由于在平坦的光滑區域內，相鄰點灰度值基本相同屬于信號的甚低頻部分，增強后輸出灰度值的變化很小;在圖像紋理區域，相鄰點灰度值有變化屬于信號的中、低頻部分，輸出灰度值將加強這種變化;在圖像的邊緣區域，鄰近的灰度值變化較大屬于信號的高頻部分，輸出灰度值將大大加強這種變化。最后利用分數階微分算子處理后圖像灰度值與原圖像灰度值相減，得到圖像經過分數階微分增強信息值，通過對比分析說明由此獲得的是具有很高信噪比的圖像紋理和邊緣信息。文獻［9］提出將W5×5分成 0°，45°，90°，135°，180°，225°，270°和315°八個方向，例如為0°方向增強算子模板，歸一化系數(1－1．5ν+0．5ν2)。將8個增強方向的最大值與W5×5增強值相比較，取其最大值視為增強后的圖像。八方向示意圖如圖2所示。

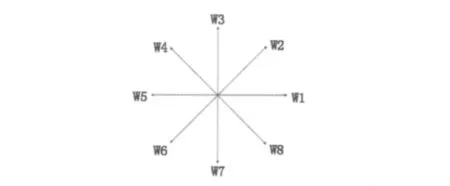
圖2 八方向示意圖

對于一階近似3×3模板W3×3為:

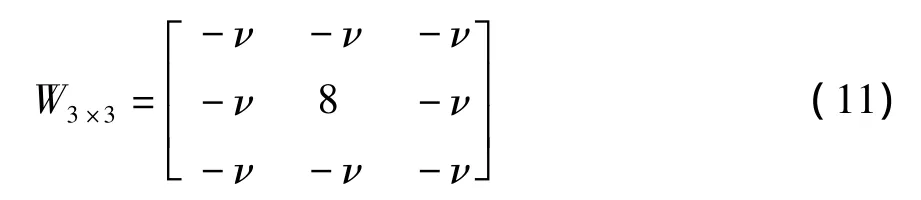
本文在3×3模板上的水平、垂直、正對角線和負對角線四個方向上，分別提出四個小模板分數階微分算子:

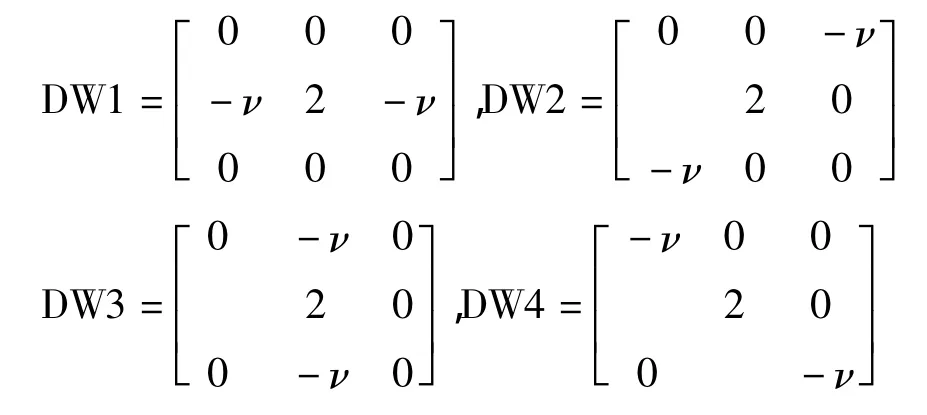
為了使得增強的圖像亮度不發生較大變化，首先將增強算子 DW1，DW2，DW3和DW4歸一化，即模板的每項除以(2－2ν)，各模板中的常系數值“2”所在的坐標(x，y)和待進行分數階微分的像素f(x，y)的坐標位置必須保持重合，將這4個方向上的模板上的系數值分別與輸入的對應像素的灰度值相乘，然后將各自的所有乘積項相加(即加權求和)，分別得到在這4個方向上的加權求和值，取4個增強方向的最大值視為增強后的圖像。

3 分數階微分圖像增強效果對比

在下面實驗中，分別采用文獻［4］、文獻［9］和本文算法對Lena中進行圖像增強，其中分數階微分為0．55 階。

文獻［4］運用分數階微分二階近似模板，在5×5窗口大小內取模板平均值為增強值。文獻［9］將5×5模板劃為八個方向的小模板，取小模板內加權和的最大值為中心點的增強值。本文改進方法運用分數階微分一階近似模板，將3×3窗口內劃為四個方向的小模板，取小模板內加權和的最大值為中心點的增強值。從圖3可知，圖3(b)雖能突出邊緣，但對帽子紋理和頭發細節增強不夠。圖3(c)對立柱下方的邊緣和帽子紋理和頭發細節增強效果明顯好于圖3(b)。圖3(d)對邊緣、紋理和細節增強效果最好，尤其在圖像右邊的小撮頭發和白色背景上方的紋理。

由于改進方法與中心點是1鄰域，而文獻［9］是2鄰域。鄰域半徑愈大的像素，與中心點像素的相關性愈小。距離中心點遠的像素會抑制中心點的變化，而距離中心點近的像素會擴大中心點的變化趨勢。所以，改進方法增強效果明顯好于其他方法。

圖4為圖3中第180行1～50列(在圖3(a)左下方白線位置)的原圖像灰度分布和三種方法增強后的圖像灰度分布。如圖4(a)所示在10～20列之間為立柱左邊邊緣，由于灰度值變化緩慢，圖4(b)雖有增強但增強幅度不大，圖4(c)增強效果較好，圖4(d)增強效果最好。在第30列附近為立柱右邊邊緣，其灰度值變化較快，從圖4可知，圖4(d)增強效果最好，圖4(c)增強效果次之，圖4(b)也有明顯的邊緣增強效果。在第40～50列附近為頭發細節，圖4(d)對頭發細節增強效果與灰度值變化較快的邊緣增強效果一樣且最好，圖4(c)增強效果次之，而圖4(b)對頭發細節的增強效果不如對灰度值變化較快的邊緣。

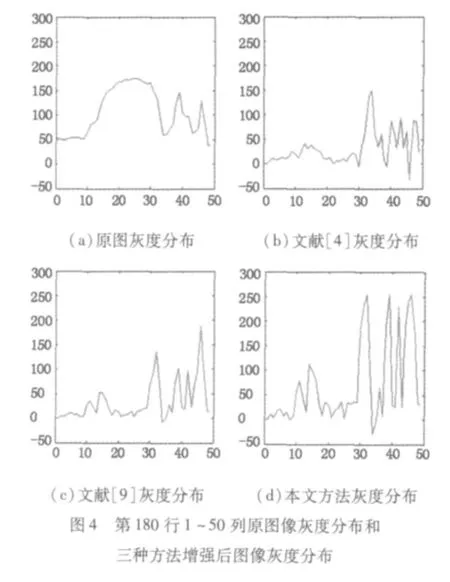
可見在文獻［4］的方法中運用分數階微分5×5模板內平均值為增強值，對邊緣增強效果好于對紋理和細節信息的增強效果。由于邊緣和紋理具有方向性，文獻［9］將5×5模板劃為八個方向的小模板，取小模板內加權和的最大值為中心點的增強值，對邊緣和紋理細節有同樣的增強效果，但增強不明顯。考慮到邊緣和紋理具有方向性，以及模板窗口越小，模板窗口內像素點的灰度值關聯性越大，本文采用3×3模板窗口并將其劃為四個方向的小模板，取小模板內加權和的最大值為中心點的增強值，對邊緣和紋理細節有同樣的增強效果，且增強幅度最大、效果最明顯。

為定量評價圖像增強效果，本文定義圖像清晰度(Definition)如下:

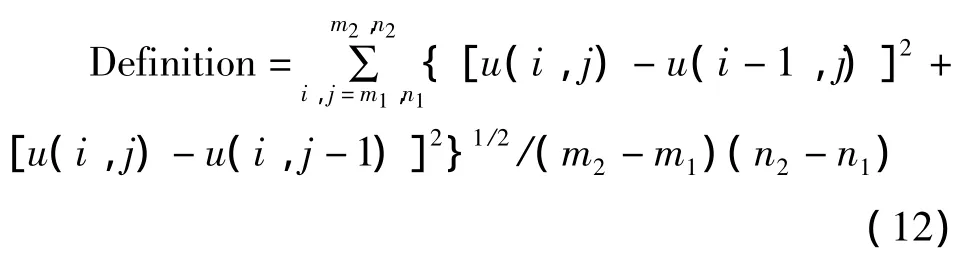
其中，u為各種算法增強后的圖像灰度值;m1，n1，m2，n2為窗口坐標。圖像清晰度取值越大表明圖像增強效果越好。表1為Lena圖像以及尺寸為4、方差分別為 0．3，0．5，0．7 高斯模糊后，對模糊圖像采用三種增強方法增強后的圖像清晰度。從表1可知，三種增強方法對原圖增強后，本文算法清晰度最大，文獻［9］次之，文獻［4］最差，與圖3的視覺效果相符。隨著高斯模糊方差增加，本文清晰度還是最大，文獻［4］最差，但其清晰度相應比對原圖增強后清晰度小，增強效果差。

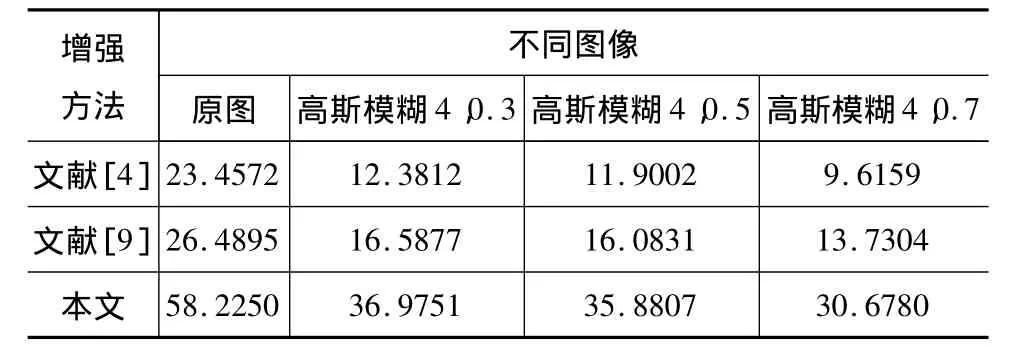
表1 圖像清晰度

4 結束語

本文在G－L分數階微分基礎上構造了ν階分數階空域微分增強算子，并用數字算法實現了該分數階微分算子。實驗表明，在相同的5×5模板窗口大小中，八方向加權和的最大值增強算法效果優于模板內平均值增強效果;模板窗口越小，模板窗口內像素點的灰度值關聯性越大，3×3模板窗口四個方向加權和最大值增強算法效果最好;本文提出的分數階增強算子能明顯地增強圖像的紋理和邊緣信息，增強后圖像清晰度提高，視覺效果明顯。

［1］ Xu Weichang，HuangWei，Li Yongfeng，et al．Application of low-pass filtering and gray adjusting to image enhancement［J］．Laser＆ Infrared，2012，42(4):458 －462．(in Chinese)

徐衛昌，黃威，李永峰，等．低通濾波與灰度值調整在圖像增強中的應用［J］．激光與紅外，2012，42(4):458－462．

［2］ Pu Yifei，Wang Weixing．Fractional differential masks of digital image and their numerical implementation algorithms［J］．Acta Automatica Sinica，2007，33(11):1128 －1135．(in Chinese)

蒲亦非，王衛星．數字圖像的分數階微分掩模及其數值運算規則［J］．自動化學報，2007，33(11):1128－1135．

［3］ Pu Yifei．Application of fractional differential approach to digital image processing［J］．Journal of Sichuan University:Engineering Science Edition，2007，39(3):124 －132．(in Chinese)

蒲亦非．將分數階微分演算引入數字圖像處理［J］．四川大學學報:工程科學版，2007，39(3):124－132．

［4］ Yang Zhuzhong，Zhou Jiliu，Yan Xiangyu，et al．Image enhancement based on fractional differentials［J］．Journal of Computer-Aided Design ＆ Computer Graphics，2008，20(3):43 －348．(in Chinese)

楊柱中，周激流，晏祥玉，等．基于分數階微分的圖像增強［J］．計算機輔助設計與圖形學學報，2008，20(3):43－348．

［5］ Pu Yifei，Zhou Jiliu，Yuan Xiao．Fractional differentia mask:a fractional differential-based approach for multiscale texture enhancement［J］．IEEE Transactions on Image Processing，2010，19(2):491 －511．

［6］ Pu Yifei．Research on application of fractional calculus to latest signal analysis and processing［D］．Chengdu:Sichuan University，2006．(in Chinese)

蒲亦非．分數階微積分在現代信號分析與處理中應用的研究［D］．成都:四川大學，2006．

［7］ Wang Chengliang，Lan Libin，Zhou Shangbo．Adaptive fractional differential and its application to image texture enhancement［J］．Journal of Chongqing University，2011，34(2):32 －36．(in Chinese)

汪成亮，蘭利彬，周尚波．自適應分數階微分在圖像紋理增強中的應用［J］．重慶大學學報，2011，34(2):32－36．

［8］ Yan Xiangyu，Zhou Jiliu．Fractional calculus applied to medical image processing ［J］．Journal of Chengdu University of Information Technology，2008，23(1):39 － 41．(in Chinese)

晏祥玉，周激流．分數階微積分在醫學圖像處理中的應用［J］．成都信息工程學院學報，2008，23(1):39－41．

［9］ Wang Weixing，Yu Xin，Lai Jun．An improved fractional differentialmask［J］．Pattern Recognition and Artificial Intelligence，2010，23(2):171 －175．(in Chinese)

王衛星，于鑫，賴均．一種改進的分數階微分掩模算子［J］．模式識別與人工智能，2010，23(2):171 －175．