利用特征線法求解方程ut+b·Du+cu=f(x,t)的初值問題
吳建成 王平心
(江蘇科技大學 數理學院,江蘇 鎮江 212003)
0 引言
1)初值問題
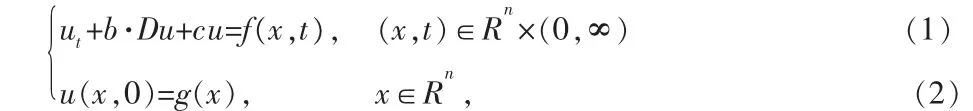
其中,c∈R1,b=(b1,b2,…,bn)∈Rn都是常數。 x=(x1,x2,…,xn)是 n維空間變量,t是時間變量 Du=(ux1,ux2,…,uxn),g(x),f(x,t)是已知函數。
2)分析
上述初值問題中的方程(1)是一階非齊次線性偏微分方程,在大多數常微分方程和偏微分方程教程中,一階偏微分方程通常受到簡單的處理,原因之一是具有很明顯應用意義的偏微分方程即位勢方程、熱傳導方程和波動方程等都是標準的二階偏微分方程。實際上,一階偏微分方程在變分法、質點力學和幾何光學中都出現過,在流體力學、空氣動力學和其它工程技術等領域有著廣泛的應用。例如在種群分析中,個體(不必是生物體,如生產的產品如燈泡、晶體管、食品或更一般的任一類似的物品的集合)根據統計樣本隨著時間的變化會變得不合格,因此研究一階偏微分方程有著實際意義。
一階偏微分方程的特點是:其通解可以通過解一個常微分方程組而得到,稱這種求解方法為特征線法[1]。而高階偏微分方程和一階偏微分方程組沒有這個特點。特征線法是一種重要又實用的方法,利用該方法證明了半有界弦振動的一維半線性波動方程的間斷初邊值問題的分片光滑解的全局存在性定理[2];用該方法給出了一類倉庫貨物儲存模型解的遞推表達式,并證明其光滑性從而得到了經典解的唯一性[3];通過運用特征線法,討論了無粘性Burgers方程柯西問題解的衰減估計,并給出了證明[4];運用特征線法給出了Born-Infeld方程的顯式表示[5]等等。特征線法除了可以運用于理論證明,也可以用于數值計算和一些實際問題的解決。
在方程(1)中令c=0,該方程退化為非齊次傳輸方程,該初值問題變為非齊次傳輸方程的初值問題。傳輸方程的初值問題已經得到解決,并且得到了古典解,受其啟示,我們來研究初值問題(1)~(2),通過推導來尋找該初值問題的古典解。方程(1)是一階偏微分方程的其中一種情況,因此我們可以利用特征線法來研究初值問題(1)~(2)。
1 解題思路
1.1 利用特征線法來求解該初值問題
初值問題有解的理論保證為下面定理:

在參數s=s0的某一領域內存在唯一解。稱這樣的解為局部解。該定理可以推廣到 n 元函數 u=u(x1,x2,…,xn)的具有如下形式的擬線性一階方程

而初值問題是要在空間 Rn+1中求滿足(3)的積分曲面 z=u(x1,x2,…,xn),使之通過如下用參數表示的n-1維超曲面γ:
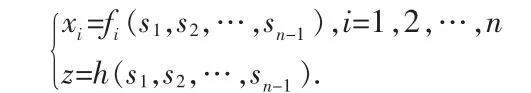
過 γ 上每一個具有參數(s1,s2,…,sn-1)的點做特征曲線,即求出

之下,就能夠由(5)前 n 個式子解出 s1,s2,…,sn-1,t,將它們代入(5)的第 n+1 個式子,就得到積分曲面 z=u(x1,x2,…,xn),它就是初值問題的解。
因為線性偏微分方程可以看作是擬線性偏微分方程的特殊情況,因此由以上對方程(3)的初值問題的處理,我們來解決初值問題(1)~(2)。

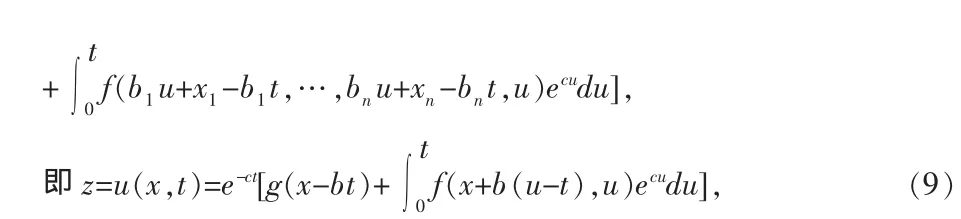
它就是我們所要求的初值問題的解。
1.2 利用特征線法的一種特殊情況求解,這是一種更直接、更直觀的求解方法

最后一步等于零是因為u滿足方程(10)。因此,函數z(s)在過點(x,t)且具有方向(b,1)∈Rn+1的直線上取常數值。 所以,如果我們知道解u在這條直線上一點的值,則就得到它沿此直線上的值。這就引出求解初值問題(1)~(2)的方法。

此即為我們所要求的初值問題的解。
因此,如果問題(1)~(2)有充分正則的解 u,它一定是由(9)式給出。 反之,容易驗證:如果 g∈C1,f∈C1,那么由(9)式定義的 u 確實是(1)~(2)的解。
以上利用特征線法把偏微分方程轉化為常微分方程求解了初值問題(1)~(2),這是一種基本又有效的方法,它不僅適用于我們本文所研究的初值問題的求解,也適用于波動方程以及其它形式的一階偏微分方程的求解。
[1]魏雪蕊.一階偏微分方程的特征線法[J].紹興文理學院學報,2010,30(7):95-97.
[2]邵志強.半線性波動方程的分片光滑解[J].福州大學學報:自然科學版,2003,31(1):6-8.
[3]孫萍,林文清.一類倉庫貨物儲存模型經典解的存在唯一性[J].新疆師范大學學報:自然科學版,2007,26(2):11-14.
[4]阮立志.無粘性Burgers方程黎曼問題光滑近似解的高階衰減估計[J].中南民族大學學報:自然科學版,2006,25(4):97-100.
[5]阮立志.Born-Infeld方程解的表示[J].中南民族大學學報:自然科學版,2005,24(3):91-92.
[6]陳祖墀.偏微分方程[M].合肥:中國科學技術大學出版社,2003:32-51.
[7]陳才生,主編.數學物理方程[M].北京:科學出版社,2009:276-283.
[8]姜禮尚,孔德興,陳志浩.應用偏微分方程講義[M].北京:高等教育出版社,2008.
[9]Lawrence C.Evans,Partial Differential Equations[M].American Mathematical Society,Graduate Studies in Mathematics,1997:18-19.

