基于包絡H?lder指數的AE信號初至時刻精確拾取

李 力，李 驥

（水電機械設備設計與維護湖北省重點實驗室（三峽大學），湖北 宜昌 443002）

0 引 言

聲發射（acoustic emission，AE）是材料內部能量釋放而產生彈性波的現象，能量釋放源即為AE源。實際結構（如鋼結構、混凝土結構）中，通常存在著裂紋、腐蝕、微動磨損等各種缺陷，這些缺陷發展時都成為AE源。為了便于技術人員及時對結構缺陷部位做出相應處理，如進行超聲復檢、焊接修復等，以避免事故的發生，對結構進行聲發射檢測（acoustic emission test，AET）以確定AE源即缺陷的位置顯得十分重要。在AET中，傳感器被陣列在結構表面，通過計算AE信號到達不同傳感器的時間差即時差定位可確定AE源的位置。因此，確定AE信號到達傳感器的準確時刻即AE信號初至時刻的精確拾取，成為AE源的時差定位中需要解決的關鍵問題之一。

AE信號的初至時刻拾取最簡單的方法是固定門檻法，即以AE信號首次超過門檻的時刻作為初至時刻，但當信號幅值較小，噪聲水平較高時，固定門檻將失效[1-2]。為此，引入浮動門檻法即STA/LTA方法，但當噪聲與AE信號頻帶相同時，初至時刻的拾取精度不高[3]。為了提高拾取精度，文獻[2]采用高階統計量法，文獻[3-4]采用了AIC準則的AR模型法，根據初至時刻前后信號幅值波動大小的差異拾取初至時刻；文獻[5]采用瞬時能量特征法，文獻[6]采用小波變換對AE信號進行時頻分析，根據初至時刻前后信號的頻率成分和能量差異拾取初至時刻。

本文將從一個新的角度——AE信號在初至時刻前后的奇異性差異，精確拾取AE信號初至時刻。并針對目前采用的描述信號奇異程度的H?lder指數無法很明顯地突出初至時刻前后信號的奇異性差異的問題，提出采用包絡H?lder指數突出差異，然后根據包絡H?lder指數在初至時刻的階躍性突變精確拾取AE信號初至時刻。

1 包絡H?lder指數估計原理

1.1 基于連續小波變換的H?lder指數估計

奇異性，是指函數或離散的時間序列在某一點上的可導程度，數學上奇異點是指那些在某一函數域里面導數不存在的點或不具有解析的點，奇異性可用H?lder指數來度量。在聲發射檢測中，AE信號到達傳感器時刻即初至時刻會表現出突變特征或奇異性，可以利用H?lder指數拾取信號的初至時刻。

基于小波變換估計H?lder指數是一種有效方法[7-9]，本文采用基于連續小波變換方法估計。信號x（t）的連續小波變換定義為

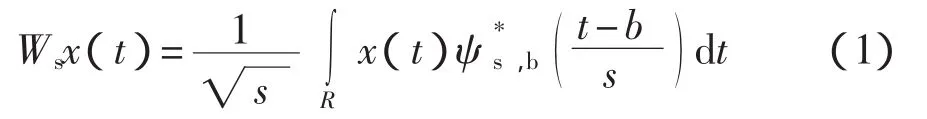
式中：Wsx（t）——x（t）的小波變換值；

對信號進行奇異性檢測，基小波應滿足在一定區間緊支撐和足夠高的消失矩階數[10]。選擇Mexicanhat小波為基小波，基小波

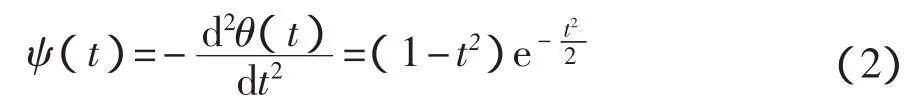
下面定義 H?lder指數。假設信號 x（t），t∈（-∞，+∞）在t0附近可以用n階多項式Pn近似表示，顯然該多項式描述了該信號的趨向。如果更高一階多項式Pn+1不能夠對信號在t0點進行近似，那么信號在t0點可由一指數α通過式（3）進行刻畫：

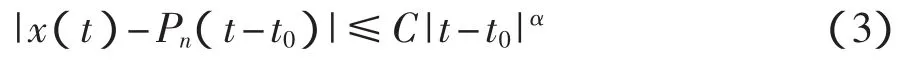
式中：Pn（t-t0）——信號用泰勒級數展開后的n階多項式；

C——常數，C|t-t0|α可以看成是信號采用n階多項式近似后的殘差，指數α稱為x（t）在點t0的H?lder指數。

根據式（3），信號 x（t）在 t0附近可表示為

其中：

由（4）式知，εt0與H?lder指數α有關，為了估計H?lder指數，需要對信號進行變換以消去多項Pn（t-t0），并保留殘差部分εt0，為此采用具有n階消失矩的小波變換：

于是對式（4）進行小波變換得

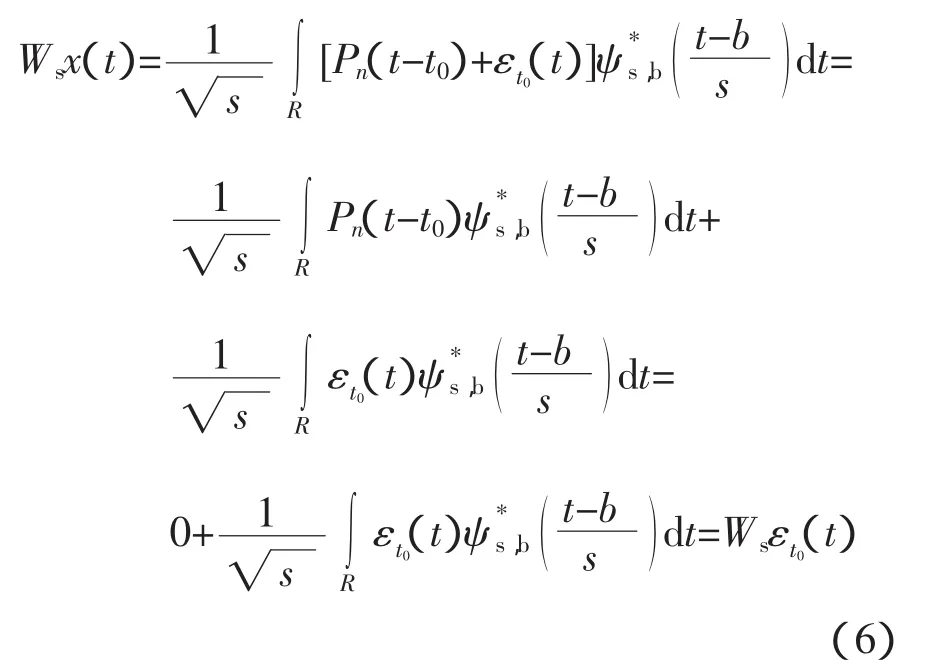
Mallat and Hwang[11]證明了在t0點附近點對所有尺度s存在一個常數A，使得：

對式（7）兩邊取對數得：

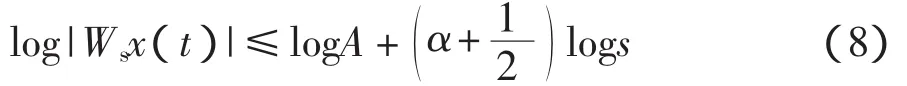
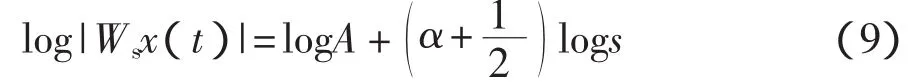
H?lder指數α可以描述信號的奇異程度，α值越大，信號的正則性越好，越光滑。

在數值計算求取α時，設信號時間序列為

在 m 個尺度水平 s1，s2，…，sm對 x（j）進行小波變換，則可以得到x（j）的小波變換值的模的二維尺度-時間矩陣：

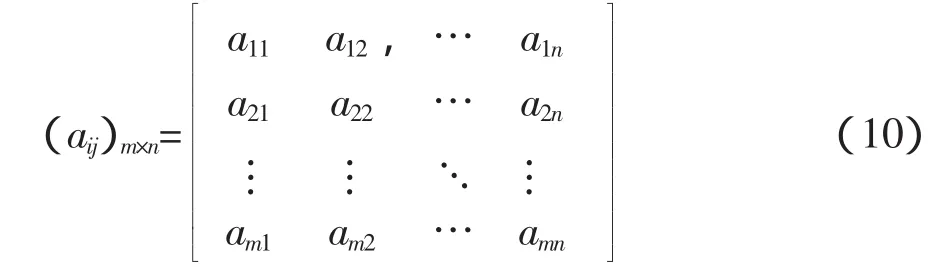
通過求小波變換值的模|Wsx（j）|與尺度s對數曲線的擬合直線斜率，得到j時刻的H?lder指數αj。

1.2 包絡H?lder指數估計算法

為了消除信號噪聲，在對信號進行H?lder指數估計時，先對測量信號求取包絡，將包絡信號作為信號來估計H?lder指數。求取包絡采用Hilbert變換[13]，圖1所示為包絡H?lder指數估計算法流程圖。

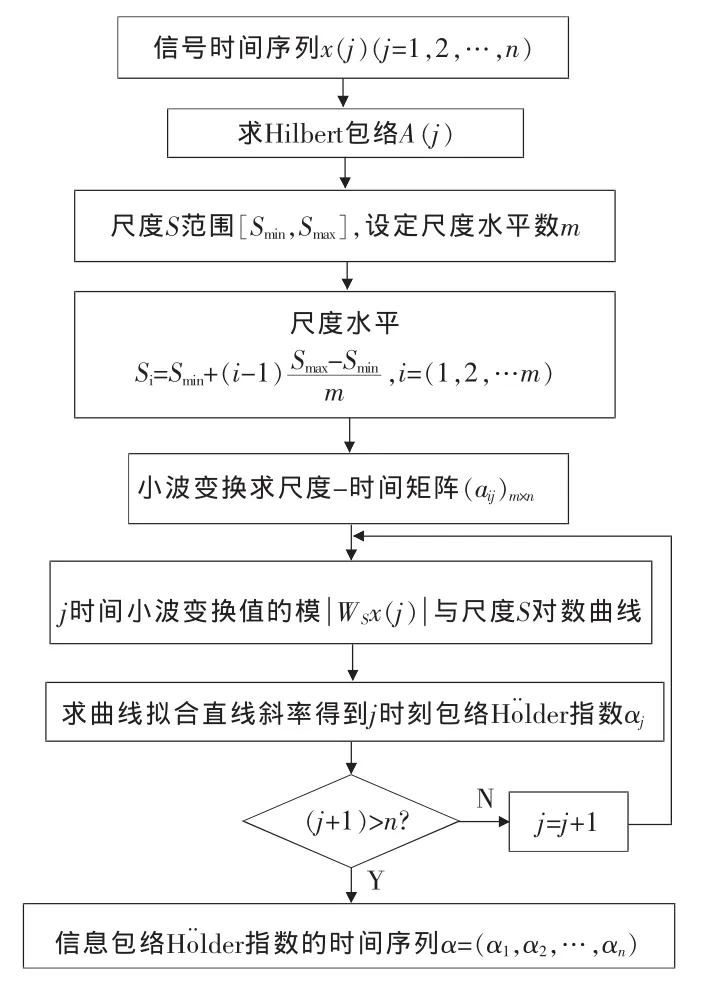
圖1 包絡Ho¨lder指數的算法流程圖

2 AE信號采集

模擬AE信號是在鋼板上采用斷鉛實驗，裂紋信號是采用圖2所示AE試驗臺對鋼板試樣進行加載試驗獲取。由于圖2試樣加載端和支撐端之間的焊接結構帶有預裂紋，當加載時裂紋發生擴展，因此，可以獲得裂紋的AE信號。信號采集使用美國PAC公司的六通道AE信號采集系統，AE傳感器為R15a共振型傳感器，采樣頻帶為20～400kHz，采樣頻率為1MHz，門檻值設為40dB。

圖2 AE試驗臺

3 AE信號的初至時刻拾取

3.1 模擬AE信號分析

斷鉛AE信號及其H?lder指數α如圖3所示。由圖3可知，H?lder指數α的極值點O在初至時刻附近，但由于初至時刻范圍內α的變化不突出，據此很難確定O點就是初至時刻。

對此信號采用包絡H?lder指數拾取，包絡H?lder指數αE如圖4（a）所示。可知，αE在O點出現明顯的階躍性突變，以O點為臨界點，αE的值整體分布在兩個水平上，且在兩個水平上都有幅度不等的波動，在O點附近波動的幅度較大，遠離O點時αE的值趨于穩定。對圖 4（a）進行局部放大，如圖 4（b）所示，可知αE出現階躍性突變的O點與AE信號初至時刻準確對應，拾取的初至時刻為341μs。

3.2 裂紋AE信號分析

采用包絡H?lder指數拾取鋼板裂紋AE信號的初至時刻。AE信號及其包絡H?lder指數αE如圖5（a）所示。可知，包絡H?lder指數αE的值在O點以前波動很大，但從O點開始，αE值迅速呈現穩定趨勢，O點的階躍性突變特征很明顯。以O為臨界點，αE整體分布在兩個水平上，αE可能會出現局部的極值，但這并不影響其整體水平的變化，這也說明局部干擾對包絡H?lder指數整體規律的變化無影響。

圖4 斷鉛AE信號及其包絡Ho¨lder指數αE變化

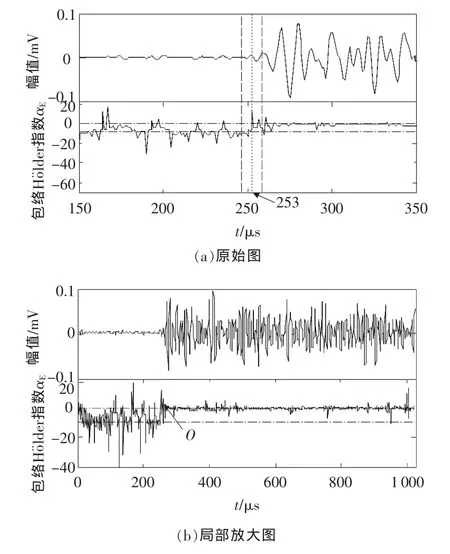
圖5 金屬裂紋擴展的AE信號及其包絡Ho¨lder指數αE變化

對圖 5（a）進行局部放大，如圖 5（b）所示，可知αE階躍性突變的O點與AE信號初至時刻準確對應，拾取的初至時刻為253μs。根據包絡H?lder指數αE的階躍性突變，對5組金屬裂紋擴展的AE信號進行初至時刻的拾取，并與從波形上手工拾取的初至時刻對比，結果如表1所示，拾取相對誤差不超過2μs。

表1 金屬裂紋AE信號的初至時刻拾取

4 結束語

（1）采用包絡H?lder指數可以突出表征AE信號初至時刻的差異，刻畫出AE信號初至時刻的細微的突變信息。

（2）對實際的斷鉛AE信號和金屬裂紋擴展的拾取AE信號初至時刻，與手工從波形拾取的結果對比，誤差不超過2μs。試驗結果證明包絡H?lder指數可以精確定位AE信號的初至時刻。

[1]馮夏庭.聲發射（AE）技術的應用[M].北京：冶金工業出版社，1997：48-51.

[2]Lokajíǒk T，Klíma K.A first arrival identification system of acoustic emission （AE）signals by means of a high-order statistics approach[J].Measruement Science and Technology，2006（17）：2461-2466.

[3]Kurz J H，Grosse C U，Reinhardt H W.Strategies for reliable automatic onset time picking of acoustic emission and of ultrasound signals in concrete[J].Ultrasonics，2005（43）：538-546.

[4]王曉偉，劉占生，竇唯.基于AR模型的聲發射信號到達時間自動識別[J].振動與沖擊，2009，28（11）：79-83.

[5]葉根喜，姜福興，楊淑華.時窗能量特征法拾取微地震波初始到時的可行性研究[J].地球物理學報，2008，51（5）：1574-1581.

[6]詹毅，鐘本善.利用小波變換提高地震波初至拾取的精確度[J].成都理工大學學報，2004，31（6）：703-707.

[7]Deng X Y，Wang Q H，Chen X K.A time-frequency localization method for singular signal detection using wavelet-based H?lder exponent and hilbert transform[C]∥2008 Congress on Image and Signal Processing，2008：266-270.

[8]李春峰.Christopher.基于小波多尺度分析的奇異性指數：一種新地震屬性[J].地球物理學報，2005，48（4）：882-888.

[9]江涌濤，張春良，胡耀斌，等.小波變換在切削顛振特征提取中的應用[J].中國測試技術，2006，32（3）：7-8，15.

[10]朱洪俊，秦樹人，彭麗玲.小波變換對突變信號峰值奇異點的精確檢測[J].機械工程學報，2002，38（12）：10-15.

[11]Mallat S，Hwang W L.Singularity detection and processing with wavelets[J].Transactions on Information Theory，1992，38（2）：617-643.

[12]Mallat S.A wavelet tour on signal processing[M].New York：Academic Press，2001.

[13]李力.機械信號處理及其應用[M].武漢：華中科技大學出版社，2007.