分布式多傳感器無源定位綜述＊

李建春 劉方正 章四兵

（電子工程學院 合肥 230037）

1 引言

分布式多傳感器無源定位可分為分布式多傳感器輻射源定位和分布式多傳感器外輻射源定位。分布式多傳感器輻射源定位主要是多個傳感器利用目標自身所輻射的信號進行定位。如圖1所示，其基本原理是多個接收傳感器分散配置，接收輻射源目標發射的電磁信號，接收傳感器通過分析、處理，提取目標的方位、時差、頻差等參數，實現對輻射源目標的定位和跟蹤。該定位體制接收傳感器分散部署，可提取方位、時差、頻差等多類參數，同時不輻射電磁波，因而其定位精度較高，同時具有“四抗”（抗干擾、抗反輻射導彈、抗低空突防和反隱身）能力。分布式多傳感器外輻射源定位則是多個傳感器利用第三方輻射源的信號（如民用的電視、廣播、通信、衛星，以及手機基站等民用輻射源等）照射到目標后的反射信號進行定位。該定位體制可看作特殊的多基地雷達系統，如圖2所示，基本原理是利用目標反射第三方輻射源的發射信號實現對目標的定位及跟蹤。該定位體制收發分置，故它具有定位精度較高及“四抗”能力等優點。

2 分布式多傳感器無源定位的特點

分布式多傳感器無源定位的特點主要表現在：1）不主動輻射電磁波信號，具有非常強的隱蔽性，生存能力強；2）系統成本較低，整個系統沒有發射模塊，只有接收裝置，故可以節省大量經費；3）多個接收傳感器可以大范圍分散部署，通過拉大站間基線長度，既可以提高定位精度，又可以擴大探測覆蓋區域；4）多個接收傳感器可以采用不同的搜索頻段，可以大大提高發現目標的概率，包括隱身目標；5）對于采取電磁靜默措施的目標，分布式多傳感器外輻射源定位體制可以利用第三方輻射源的機會照射，實現對目標的檢測、參數測量、定位及跟蹤。

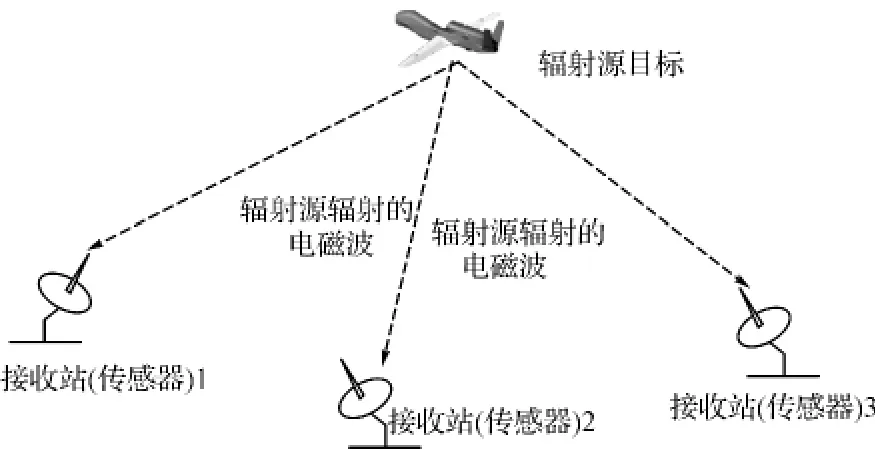
圖1 分布式多傳感器輻射源定位示意圖

3 相關研究現狀

3.1 分布式多傳感器輻射源定位的研究狀況

分布式多傳感器輻射源定位在民用和軍事應用方面都得到了迅猛的發展。大多數國家都對尤其是西方發達國家的跨國公司，比如Motorola、Nokia、Ericsson等積極地開展對基于GSM、IS-95和第三代移動通信系統的定位技術的研究，并且制定了相應的實施方案及行業標準（如GSM系統中選用的增強觀測時差（E-OTD）定位法；WCDMA 系統中選用OTDOA-IPDL定位法［1］。）同時分布式多傳感器輻射源定位在軍事應用上也已研制出了許多裝備［2］。俄羅斯的“MCS-90系統”是一個由三接收站構成的無源探測系統，利用時差定位原理實現對目標的定位及跟蹤。烏克蘭的“卡拉秋塔”系統，它有單站、三站兩種結構形式，單站系統主要用來探測對方無線電信號，對所截獲的信號進行分析、識別，在其構建的防空體系中擔負早期預警任務，三站系統可對600km 內的低空目標進行定位并且可標繪其航跡。捷克的“TAMANA”系統是三站時差定位系統，可對空中、地面和海面目標進行定位、識別與跟蹤，并可以實時提供目標點跡、航跡。其各站的基線長度為10km～35km，探測距離大于400km。捷克的“VERA-E”系統，在較寬的頻帶范圍內處理各種輻射源電磁波信號，“VERA-E”系統由適當部署的三接收站或四接收站組成，采用時差定位技術來確定目標的位置，是目前比較成熟和實用的分布式無源定位系統。以色列的“EL／L-8388”對空早期預警系統，采用短基線時差定位體制，工作頻段0.5GHz～18GHz，其時差估計精度最高可達1ns。

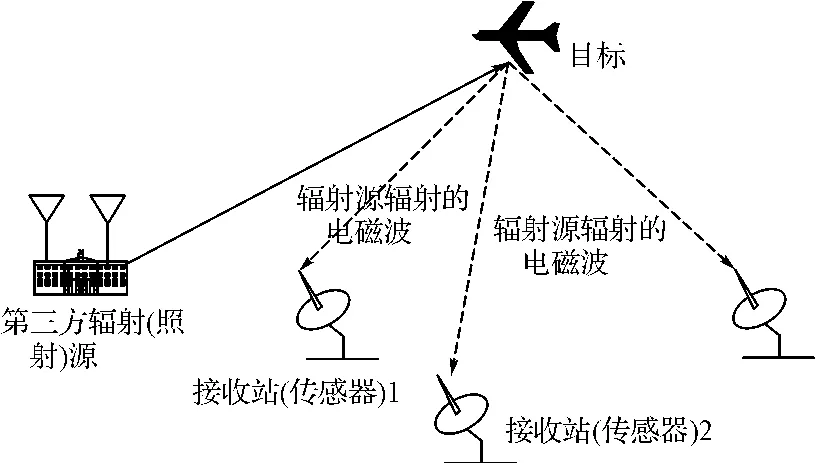
圖2 分布式多傳感器外輻射源定位示意圖

3.2 分布式多傳感器外輻射源定位的研究狀況

分布式多傳感器外輻射源定位系統主要有［3］：法國國家航空研究局以巴黎的埃菲爾電視臺廣播信號作為外輻射源信號，構建了非合作無源雷達試驗系統；德國西門子公司利用民用電臺信號作為外輻射源信號，構建了無源雷達試驗系統；英國防御研究局利用電視音頻調幅載波信號作為外輻射源信號，構建了無源雷達試驗系統；較為成熟的系統是美國洛克希德·馬丁公司利用調頻廣播信號和電視信號作為第三方輻射源信號的“沉默哨兵”分布式無源探測定位系統。“沉默哨兵”系統的工作原理［4］：利用商業調頻電臺和電視臺發射的50MHz～800MHz連續波信號，檢測、跟蹤、監視任務區內的運動目標。該系統由大動態范圍數字接收機、相控陣接收天線、高性能并行處理器及相關軟件組成。該系統能夠跟蹤到180km～220km 的反射面積為10m2的目標，并且能同時跟蹤200個以上目標，分辨率為15m。該系統有120°的觀察范圍，采用數字波束形成技術實現整個扇區覆蓋，可跟蹤固定翼飛機、旋翼機、巡航導彈和彈道導彈。系統的核心是“無源相控定位技術”，系統自身不輻射電磁波，這種靜默的工作模式使得系統可以躲避對方的偵察裝備和反輻射導彈，保證了自身安全。

4 分布式多傳感器無源定位的關鍵技術

4.1 分布式無源定位技術

在分布式無源定位技術中，直接根據接收的輻射源目標信號（無需參數估計）得出目標位置，該方法稱為直接定位法［5］，也可首先對輻射源目標信號進行參數估計，然后利用相關參數（到達時間、頻率等）對目標位置進行估計，該方法稱為兩步定位法［6］。

基于參數估計的兩步定位技術可以分為種，一種是基于數據庫的映射方法，該類算法需在定位之前的訓練階段建立所需要的數據庫［7］；另一種是基于幾何或統計的方法。其中基于數據庫定位技術的計算量比較大，不具備實時性。一般工程上都采用基于幾何或統計的定位方法。幾何定位方法先利用單一或多個測量參數確定出定位曲線或曲面，再通過計算多條定位曲線或曲面的交點來確定目標的坐標。例如，由TOA 參數得出的距離信息，可以確定的定位線為一個圓或球。對于TDOA 參數而言，每個測量參數對應一條雙曲線或雙曲面，確定雙曲線或雙曲面的交點即完成目標位置的估計。幾何定位方法可以應用于混合系統，如TDOA／AOA［8］和TOA／TDOA［9］等。但是在幾何定位方法中認為所有測量參數均為真實值，因此多條定位線或面才會相交于一點。然而在實際情況下，所有的量測參數均疊加了噪聲，噪聲屬于隨機誤差，因此多條定位線或面實際上相交于某一個區域。相比較而言，統計定位方法則具有更廣的適用范圍［10］。所謂統計定位方法，即根據量測參數、誤差的先驗誤差模型建立代價函數，如測量方程或似然函數，然后利用貝葉斯或最大似然進行處理［11］。

直接定位是一種通過建立代價函數，采用二維平面搜索直接解算出信號中包含的目標位置信息的方法。該方法避免了傳統定位法兩步定位的缺陷，且不要求傳感器間的時間同步，但現有工作在研究時僅考慮了目標傳送信號到傳感器的信道衰減及干擾，而忽視了由傳感器傳送信號到另一傳感器（或定位中心）這一過程的影響，且直接定位算法的計算復雜度遠遠高于兩步定位技術。

4.1.1 AOA（Angle Of Arrival）技術

AOA 是使用陣列天線來估計信號到達方向對目標位置進行估計。一個AOA 測量值可以確定目標輻射源的一個角度方向，如果至少有兩次不同地點的有效測量，則輻射源的位置就可以利用兩個角度方向相交確定出來。通常，可以利用多個地點的AOA 測量值來提高測量的精度。AOA 方法雖然原理簡單，但它存在一定的缺陷，為了得到精確的AOA 估計，關鍵的一點就是信號從發射點到天線需是LOS（Line Of Sight）傳播，因此對于非視距NLOS（Non Line Of Sight）信道存在一定困難。AOA 的測量設備都是多天線系統，各通道之間的一致性要求很高，設備不但昂貴而且笨重。而且AOA 估計算法的復雜度較高，用于測量、儲存、處理等會占用過多的軟硬件資源。

4.1.2 TOA（Time Of Arrival）技術

TOA 是通過測量輻射源目標和接收機之間的絕對到達時間實現對目標的定位。將信號的時延乘以光速得到輻射源目標與接收機之間的距離，測量該輻射源目標和多個接收機之間的距離得到定位方程組，則輻射源目標位于以接收機為圓心，目標與接收機之間的距離為半徑的圓上。TOA 定位的實現要求輻射源與接收站之間嚴格時間同步，以求得輻射源信號的絕對到達時間。

4.1.3 TDOA（Time Difference of Arrival）技術

TDOA 是測量輻射源目標到不同接收站之間的到達時間差而進行定位的。為了測量信號的到達時差，各接收站之間必須精確同步。TDOA 值可以定義一條以兩個基站為焦點的雙曲線，目標輻射源就位于雙曲線上。在TDOA 定位算法研究方面，目前已提出多種具有不同精度和計算復雜性的定位算法［1］，如Fang算法、SX 和SI算法、Friedlander算法、分類征服、DAC 算法、采用兩步WLS 的Chan 算法、泰勒級數展開法、近似最大似然估計（AML）算法［12］等，其中以Chan算法、泰勒級數展開法和AML 算法精度最高。Chan算法是一種具有解析表達式解的非遞歸的雙曲線方程組解法，該算法的特點是計算量小，適合于三傳感器及多傳感器，在噪聲較小且服從高斯分布的情況下，定位精度高。但在TDOA 測量誤差較大或在一定的幾何布局下，Chan算法的定位精度會顯著下降。泰勒級數展開法是一種需要初始位置的遞歸算法，該算法的特點是能適用于各種信道環境，在初始估計位置與實際目標位置接近的情況下，定位精度高，但是在初始位置選擇不好或者一定的幾何布局下，算法有可能不收斂。結合Chan算法和泰勒級數展開法各自的長處，將它們融合在一起，先用Chan算法求取目標輻射源初始位置，然后在此初始位置基礎上通過泰勒級數展開法得到精確估計位置［13］。Y.T.Chan最新提出了AML定位算法，其文中的仿真結果驗證了此算法接近最優，在不同幾何布局條件下定位精度能達到克拉美羅下限，但由于也需要多次計算，所以計算量也較大。

4.1.4 FDOA（Frequency Difference of Arrival）技術

FDOA 技術是通過測量各接收機之間所接收信號的多普勒頻率差來進行定位的。其常應用于衛星對地觀測定位上，因為除了地球同步衛星以外，其它的衛星相對地球上的物體是有相對運動的，這樣輻射源信號到達各顆衛星時就會產生多普勒頻移，又由于衛星位置不一樣所以這些多普勒頻移是不一樣的，則形成了FDOA。每一個FDOA 在三維空間將對應于一個曲面，各個FDOA 曲面的交點就是目標輻射源的定位位置。

4.1.5 混合定位技術

這種方法是利用上述兩種或者多種不同類型的信號特征測量值來實現定位，如TOA／AOA、TDOA／AOA、TDOA／TOA 等組合進行定位估計。

4.1.6 概率定位技術

從概率的角度出發，將4.1.1節到4.1.5節的參數量測方程，看作求解輻射源位置落在空間中概率最大的點或區域。在三維空間中，每一個方位角或俯仰角測量值確定一個平面，每一個TDOA 測量值確定空間中一對以兩站為焦點的雙曲面。由于現實中存在測量誤差，可以將定位問題視為位置估計問題。既然是位置估計問題，那么就要考慮概率分布。顯然，輻射源的位置估計的概率分布不為均勻分布，如果測量值是方位角或者俯仰角，那么目標位置估計落在一個平面上的可能性比落在其它區域的可能性要大一些，如果測量值是TDOA，那么目標估計值落在一個雙曲面上的可能性比落在其它區域的可能性要大一些。多個角度（方位角、俯仰角）、TDOA 測量形成了多個子集，假定多次測量相互獨立，那么目標可能從某個位置輻射信號的概率為多次測量所對應的概率之積。結合輻射源高度信息，那么概率之積最大所對應的位置就是目標的位置估計。

4.1.7 直接定位技術

傳統的定位技術（4.1.1節到4.1.6節）要先估計TOA、AOA 和TDOA 等測量參數，然后利用幾何關系計算輻射源目標的位置，其定位精度取決于第一步參數測量的精度和第二步位置解算算法的性能，在測量TOA 時還須保證多傳感器間的時間同步。為克服傳統兩步定位方法的困難，近年來Anthony J Weiss提出了無需測量參數估計的直接定位方法［14～15］。直接定位是一種通過建立代價函數（cost function），采用二維平面搜索直接解算出信號中包含的輻射源目標位置信息的方法。該方法避免了傳統定位法兩步定位的缺陷，且不要求傳感器間的時間同步，但現有工作在研究時僅考慮了輻射源目標傳送信號到傳感器的信道衰減及干擾，而忽視了由一個傳感器傳送信號到另一個傳感器（或定位中心）這一過程的影響，因而直接定位技術的計算復雜度要遠高于傳統定位技術。

4.2 非線性濾波技術

單純利用分布式多傳感器無源定位技術不足以獲取運動目標連續的位置信息，對于運動目標而言需要進行有效的跟蹤濾波。大多數無線傳感器的測量數據與目標狀態間常呈非線性關系。如果利用觀測數據完成目標狀態的更新，必須解決非線性濾波問題。解決非線性濾波問題的方法主要分為兩類，一類是將非線性問題線性化，即對高階項采用截斷或逼近的方法；另一類則是利用采樣的方法來近似非線性分布。

Anderson和Moore就利用上述思想將Kalman濾波推廣到非線性濾波的場合，提出了擴展卡爾曼濾波（EKF），并得到了廣泛的應用。EKF 算法不再是按照某個指標去進行優化的優化算法，其性能很大程度上取決于非線性的復雜程度。因此，若非線性函數的泰勒級數展開式的高階項較大，無法忽略的時候，線性化所導致的誤差會很大，從而影響濾波的性能。針對上述存在的問題，有學者改進了EKF算法（如高階截斷EKF、迭代EKF［16］等）。相比較非線性函數的線性化近似非線性函數的概率分布要更加容易，其中UKF 和PF 是兩種最具有代表性的方法。Juher等人提出的無跡卡爾曼濾波（UKF）算法［17］以UT 變換為基礎，以Kalman濾波為框架，使用確定性采樣獲取非線性函數的概率分布。相比較EKF算法，UKF具有如下優點：對非線性函數的概率密度進行近似，而不是非線性函數的近似；非線性分布統計量的計算精度至少達到2階；不需要計算雅可比行列式，且運算量與EKF 同階；可以處理非加性的噪聲以及離散的系統。目前，UKF被廣泛應用于機器人自主定位、地面車輛導航和跟蹤等。粒子濾波算法（PF）［18］是近年來興起的最優非線性濾波方法，其通過隨機采樣策略，對狀態空間直接進行采樣，獲取相互獨立的隨機粒子來表征后驗概率密度，繼而利用新的觀測對后驗概率密度進行更新。為了進一步提高粒子濾波算法的性能，一系列的改進算法被相繼提出，如序貫重點采樣算法、重點采樣重采樣算法SIR 和SIR-MCMC［19］等。

4.3 數據關聯技術

分布式多傳感器無源定位技術為實現多目標的可靠跟蹤，則需要首先完成數據的可靠關聯。多維分配算法是實現數據關聯的一類重要手段。多維分配算法主要包括2-D 分配算法和S-D分配算法［20］。其中2-D分配算法用于解決“觀測值一航跡”間關聯的問題；而S-D 分配算法則處理多傳感器觀測數據間的“觀測值一觀測值”關聯問題。對于2-D 分配問題而言，常用的解法包括拍賣算法，JVC算法，以及用于網絡流量的Relax方法。其中，拍賣算法在目標稀疏的場景下速度比JVC算法快，但是在目標較為密集的場景中，JVC算法的性能則要優于拍賣算法。與2-D分配問題相類似，SD分配問題是一個NP-Hard問題。利用其它NP-Hard問題次優解的方法，如貪婪消源法，模擬退火法等，求解S-D分配問題的次優解，會存在大量錯誤的關聯結果。Deb［21］，Poore［22］以及Pattipati［23］提出了一種具有可量化精度的快速多層拉格朗日解法。該方法將S-D 分配問題化簡為一系列的2-D分配問題進行求解，將多維優化問題引入S-D分配算法中，提出了多傳感器廣義S-D 分配算法，該方法利用最大似然的方法，避免了窮舉搜索，提高了分配算法的運算效率。

另外，可應用后驗概率貝葉斯方法解決“觀測值—航跡”間關聯的問題，如聯合概率數據關聯法（JPDA）［24］、多假設跟蹤（MHT）和概率多假設跟蹤（PMHT）［25］等，上述方法具有計算量小、性能好等優點，且易于工程實現，因而備受研究人員的親睞。近些年來，越來越多的研究將其它數學工具應用于數據的關聯，從而產生新的配對算法，如聚類方法［26］，Viterbi數據關聯算法（VDA）等。對于數據分配算法而言，計算的瓶頸不在獲得次優數據關聯的計算，而在于關聯算法的運算量，因此對于數據關聯算法的研究主要表現在兩方面，一方面是將新的數學理論引入數據關聯中，如證據理論和隨機集理論等［28］，從而擺脫傳統的貝葉斯理論框架；另一方面則是提高數據分配算法的計算效率，降低算法的復雜程度。

5 結語

分布式多傳感器無源定位不僅可以有效地抗擊電子干擾、隱身技術、反輻射武器等威脅，而且具有精度高、覆蓋空域廣、能對付寬帶低譜密度信號等優點，使其在軍事、為移動臺提供定位服務、無線電監測定位上都具有巨大應用潛力。因此，在未來的戰爭或復雜條件下的目標定位跟蹤及識別中，分布式多傳感器無源定位技術將會得到越來越廣泛的發展和應用。

［1］范平志，鄧平，劉林.蜂窩網無線定位［M］.北京：電子工業出版社，2002.

［2］劉月華.時差定位無源雷達的系統設計［D］.南京：南京理工大學，2003.

［3］唐小明，何友.基于機會發射的無源雷達系統發展評述［J］.現代雷達，2002，24（2）：1-6.

［4］溫中武，宋闊益.電子對抗中無源雷達的地位和發展前景［J］.國防科技，2007，1（9）：14-18.

［5］A.J.Weiss.Direct position determination of narrow band radio frequency transmitters［J］.IEEE Sig.Processing Lett，2004，（11）：672-681.

［6］J.J.Caffew.Wireless Location in CDMA Cellular Radio Systems［M］.Boston：Kluwer Academic Publisher，2000.

［7］C.Nerguizian，C.Despins and S.Affes.Geo-location in mines with an impulse response fingerprinting technique and neural networks［J］.IEEE Trans.Wireless Commun，2006（5）：603-611.

［8］L.Cong and W.Zhang.Hybrid TOA／AOA mobile user location for wideband CDMA cellular systems［J］.IEEE Trans.Wireless Commun，2002，（1）：439-447.

［9］R.I.Reza.Data fusion for improved TOA／TDOA position determination in wireless systems［D］.Ph.D.Dissertation，Virginia Tech，2000.

［10］H.V.Poor.An Introduction to signal detection and estimation［M］.New York：Springer-Verlag，1994.

［11］S.Al-Jazzar and J.J Caffery.ML and Bayesian TOA location estimators for NLOS environments［C］／／in Proc.IEEE Ini.Conf.Veh.Technol，Vancouver，BC，2002：1178-1181.

［12］Y.T Chan，Herman Yau Chin Hang，Pak-chung Ching.Exact and approximate maximum likelihood localization algorithms［J］.IEEE Trans on VTC，2006，55（1）：10-16.

［13］劉林，鄧平，范平志.基于Chan氏算法和Taylor級數展開法的協同定位方法［J］.電子與信息學報，2004，26（1）：41-46.

［14］Oispuu M，Nickel U.Direct detection and position determination of multiple sources with intermittent emission［J］.Signal Processing，2010，90（12）：3056-3064.

［15］Weiss A J.Direct position determination of narrowband radio frequency transmitters［J］.IEEE Signal Processing Letters，2004，11（5）：513-516.

［16］A.Gernlani，C.Manes and P.Palunlbo.Polynomial extended Kalman filter［J］.IEEE Trans.AES，2005，（29）：1015-1022.

［17］K.Xiong，H.Y.Zhang and C.W.Chan.Performance evaluation of UKF-based nonlinear filtering［J］.Automatica，2006，（42）：261-270.

［18］C.Kwork，D.Fox and M.Meila.Real-time particle filters［J］.Proceedings of IEEE，2004，（92）：496-484.

［19］F.Gustafsson，F.Gunnarsson and N.bergman.Particle filters for positioning，navigation，and tracking［J］.IEEE Trans.SP，2002，（50）：425-426.

［20］Y.Bar-Shalom and W.D.Blair.Multitarget-multisensor tracking application and advances［M］.Boston：Artech House，2000.

［21］S.Deb.A generalized S-D assignment algorithm for multisensor-multitarget state estimation［J］.IEEE Trans.AES，1997，（33）：523-538.

［22］A.Poore and A.J.Robertson.A new class of lagrangian relaxation based algorithms for a class of multidimensional assignment problems［J］.Computational optimization and application，1997，（3）：544-563.

［23］K.R.Pattipati，S.Deb and Y.Bar-Shalom.A new relaxation algorithm and passive sensor data association［J］.IEEE Trans.Automatic Control，1992，（37）：198-212.

［24］T.K.Y.Bar-Shalom，X.Lin.Probabilistic data association techniques for target tracking with application to sonar，radar and EO sensors［J］.IEEE Journal of Oceanic Engineering，2005，（20）：37-55.

［25］尹成友.基于多傳感器的近程目標高精度定位與跟蹤的研究［D］.中國科學技術大學博士學位論文，2003.

［26］S.Theodoridis and K.Koutroumbas.模式識別［M］.北京：電子工業出版社，2006.

［27］戴邵武，馬長里，代海霞.北斗雙星／SINS組合導航中的捷聯慣導算法研究［J］.計算機與數字工程，2010，38（2）.

［28］韓崇昭，朱洪艷，段戰勝.多源信息融合［M］.北京：清華大學出版社，2006.