在實(shí)驗(yàn)室條件下測量倏逝波的貫穿深度
翟曉靈,萬 牛,王秋紅,邵漢森,潘永華
(南京大學(xué) 物理學(xué)院,江蘇 南京210046)
1 引 言
光從光密介質(zhì)入射到光疏介質(zhì)時(shí),若入射角大于臨界角,在介質(zhì)分界面處會(huì)發(fā)生受抑全反射現(xiàn)象[1],但光并不是直接全部反射回光密介質(zhì),而是有一部分光進(jìn)入光疏介質(zhì),即在光疏介質(zhì)內(nèi)會(huì)出現(xiàn)倏逝波.倏逝波具有快速衰減的特性[2],在傳播很小一段距離(即貫穿深度[2])的過程中慢慢全部返回光密介質(zhì).經(jīng)過理論推導(dǎo),貫穿深度在102nm量級(jí),一般很難測量其大小.目前研究倏逝波的實(shí)驗(yàn)大多采用的是基于較高工藝手段制作出來較精確的102nm量級(jí)厚度的薄層[3],在大學(xué)物理實(shí)驗(yàn)室無法滿足此要求的情況下,本實(shí)驗(yàn)采用平凸透鏡與平面玻璃鏡的組合結(jié)構(gòu)(以下簡稱組合裝置)[3],構(gòu)造出符合實(shí)驗(yàn)要求的空氣薄層,并且在此基礎(chǔ)上設(shè)計(jì)了可調(diào)節(jié)平凸透鏡與平面玻璃鏡間距的新組合裝置,使得在一般實(shí)驗(yàn)條件下即可測量倏逝波的貫穿深度.
2 貫穿深度相關(guān)公式推導(dǎo)
2.1 倏逝波貫穿深度的理論推導(dǎo)
入射平面電磁波[4]為
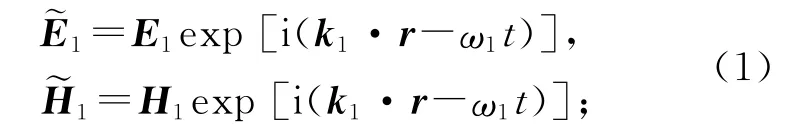
反射平面電磁波為
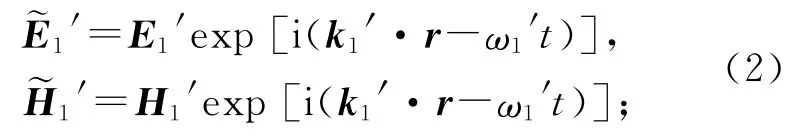
折射平面電磁波為
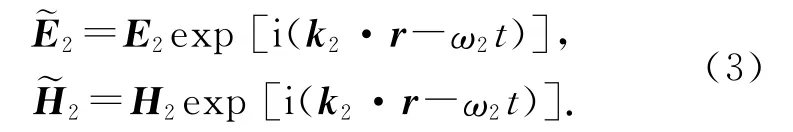
對(duì)于2種不同折射率的介質(zhì),在分界面上有邊界條件[5]:

取介質(zhì)分界面為z軸,若要滿足對(duì)所有的x,y,t邊界條件(4)都成立,則需要滿足:
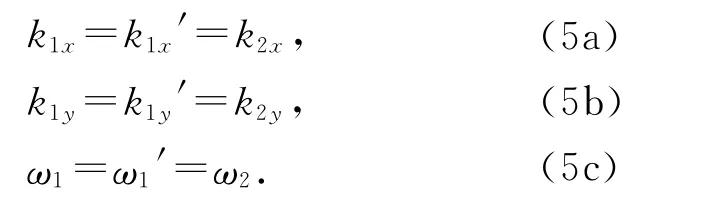
取x軸在入射面內(nèi),則式(5b)可寫為
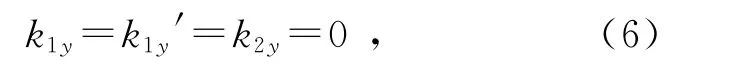
即反射線、折射線與入射線在同一平面(入射面)內(nèi);由式(5c)可知,反射光、折射光與入射光的頻率相同,記為

設(shè)入射角、反射角和折射角分別為θ1,θ1′,θ2,則有
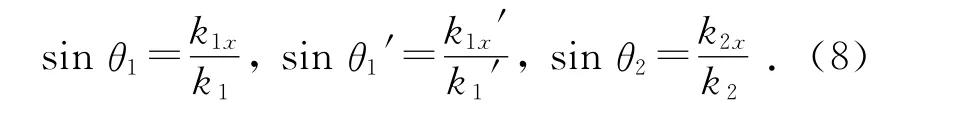
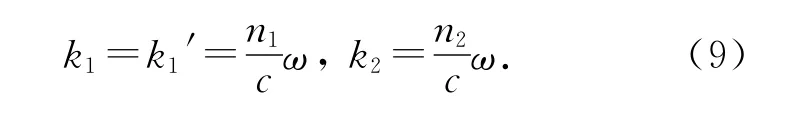
由式(5)~(9)可推出折射波矢的z分量為
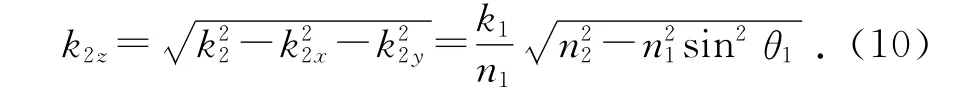
由(10)式可知,當(dāng)k2z=0時(shí),入射角達(dá)到臨界角θc時(shí),介質(zhì)分界面開始出現(xiàn)全反射現(xiàn)象;若入射角大于臨界角θc,k2z將成為虛數(shù),記為iκ,則

其中λ為真空中光波長.此時(shí)介質(zhì)n2中波的表達(dá)式化為
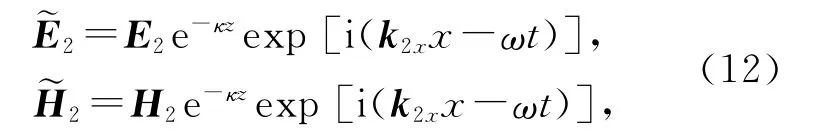
(12)式表明在發(fā)生全反射時(shí),折射光在x方向(沿界面)仍具有行波形式,但沿z方向(縱深方向)按指數(shù)急劇衰減,故在介質(zhì)n2中的有效貫穿深度定義為
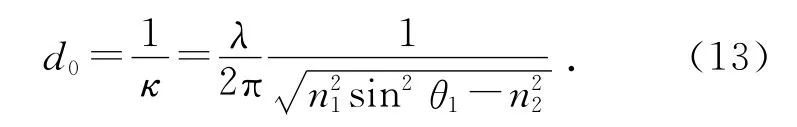
2.2 倏逝波貫穿深度的實(shí)驗(yàn)推導(dǎo)
由于倏逝波具有快速衰減的特性,需要做出可以和波長量級(jí)的貫穿深度相比較的微小間隙,采用平凸透鏡和平面玻璃鏡組合的裝置,利用平凸透鏡的曲率性質(zhì)即可解決.組合裝置見圖1.組合裝置中的幾何關(guān)系如圖2所示,當(dāng)平凸透鏡與平面玻璃鏡接觸時(shí),空氣薄膜的厚度d為零,此時(shí)的倏逝波會(huì)通過平凸透鏡出射,因此在另一側(cè)就能觀察到中心亮斑.而當(dāng)空氣薄膜厚度d不為零且由零逐漸增大到貫穿深度d0時(shí),由于倏逝波的衰減特性中心亮斑會(huì)慢慢變小直至消失.調(diào)節(jié)平凸透鏡和平面玻璃鏡的距離,當(dāng)亮斑剛好消失時(shí)停止,此時(shí)采用等厚干涉牛頓環(huán)實(shí)驗(yàn)裝置[6],測量出組合裝置形成的各級(jí)牛頓環(huán)直徑即可算出貫穿深度d0.
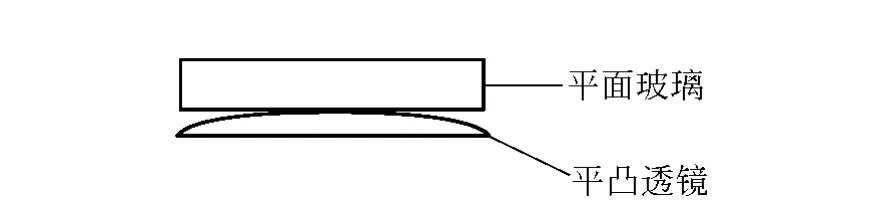
圖1 組合裝置
假設(shè)從中心往兩邊數(shù)第k級(jí)暗紋對(duì)應(yīng)的空氣薄膜厚度為Hk,則有
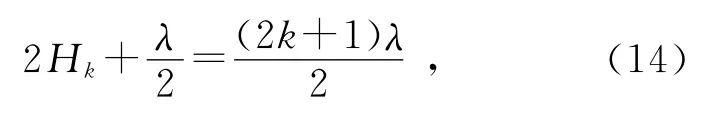
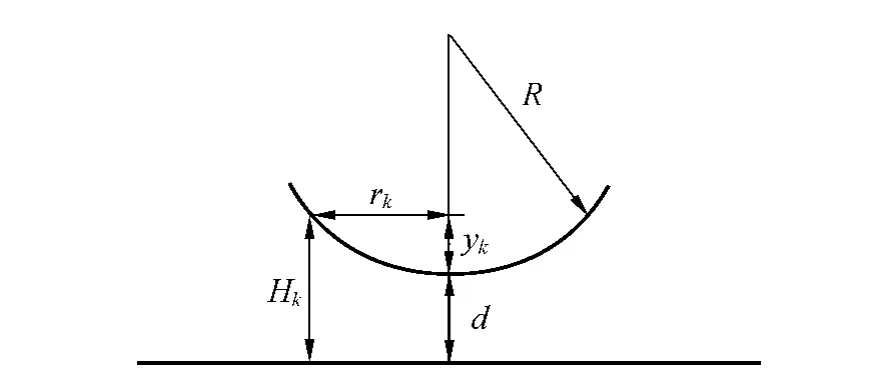
圖2 組合裝置中的幾何關(guān)系
暗紋半徑為rk,yk,如圖2所示,平凸透鏡曲率半徑R已知(亦可通過實(shí)驗(yàn)進(jìn)行測量[6]),則空氣薄膜中心厚度

其中R,rk,yk滿足關(guān)系
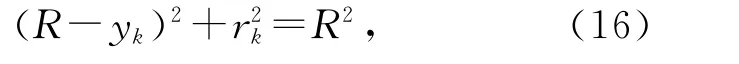
通過式(14)~(16)即可得出貫穿深度

3 實(shí)驗(yàn)結(jié)果與分析
實(shí)驗(yàn)采用“直角棱鏡1— 組合裝置—直角棱鏡2”裝置,光路如圖3所示.
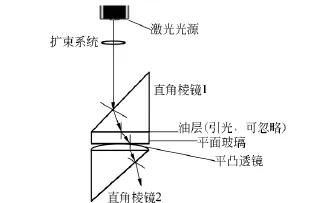
圖3 實(shí)驗(yàn)光路圖
圖3中2個(gè)直角棱鏡是為了調(diào)節(jié)光路,引導(dǎo)光進(jìn)入組合裝置.組合裝置的外部還加裝可調(diào)螺絲的固定銅環(huán),通過調(diào)節(jié)螺絲可以實(shí)現(xiàn)對(duì)平凸透鏡與平面玻璃鏡的距離d的調(diào)節(jié).組合裝置內(nèi)光路如圖4所示,其中光源采用632.8nm的He-Ne激光.
由倏逝波貫穿深度的理論推導(dǎo)式(13)可知,當(dāng)入射光波長λ1(即為真空中光波長λ)、光密介質(zhì)折射率n1和光疏介質(zhì)折射率n2一定時(shí),貫穿深度只和入射角θ有關(guān),因此需要知道平凸透鏡界面入射角的大小.由于采用了直角棱鏡引光,故先推導(dǎo)直角棱鏡界面入射角α1與平凸透鏡界面入射角α4的關(guān)系,如圖4所示.在直角棱鏡界面和平凸透鏡界面由折射定律得
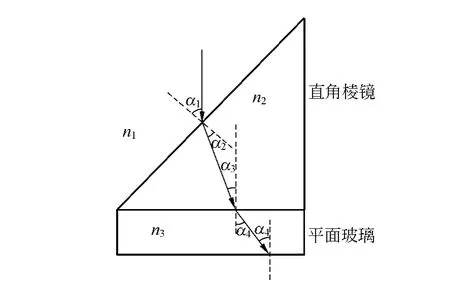
圖4 組合裝置簡化光路圖

其中α2+α3=π/4,空氣折射率n1=1,直角棱鏡折射率n2=1.661,牛頓環(huán)折射率n3=1.52.
實(shí)驗(yàn)時(shí),首先調(diào)節(jié)組合裝置,使得入射光在第一塊直角棱鏡斜邊上的反射光恰好可以和入射光重合,即入射光垂直入射在直角棱鏡斜邊上,將此時(shí)入射光在直角棱鏡上的入射角α1=0記為零角.繼續(xù)調(diào)節(jié)入射角α1至看到明顯的透射光牛頓環(huán)為止,此時(shí)未發(fā)生受抑全反射;再向著相反的方向調(diào)節(jié)入射角α1,會(huì)發(fā)現(xiàn)牛頓環(huán)往外擴(kuò)大,直至牛頓環(huán)完全消失,此時(shí)發(fā)生受抑全反射,只能觀察到中央亮斑.然后固定并記下入射角方位,調(diào)緊螺絲,透射光中央亮斑很大,此時(shí)平凸透鏡與平面鏡緊密接觸;再慢慢調(diào)松螺絲,會(huì)發(fā)現(xiàn)中央亮斑慢慢縮小;繼續(xù)調(diào)節(jié)螺絲直到中央亮斑剛好消失停止,此時(shí)平凸透鏡與平面玻璃鏡的距離d即為貫穿深度d0.將裝置放在牛頓環(huán)實(shí)驗(yàn)顯微鏡下,用波長589.3nm的鈉光燈測量其等厚干涉各級(jí)暗環(huán).由式(13)~(18)分別可以計(jì)算出理論數(shù)據(jù)和實(shí)驗(yàn)數(shù)據(jù),部分計(jì)算結(jié)果如表1所示.

表1 貫穿深度部分測量數(shù)據(jù)
由表1所示的理論計(jì)算值與實(shí)驗(yàn)計(jì)算值可以看出,雖然運(yùn)用此種方法測量的結(jié)果與實(shí)際結(jié)果有一定的誤差,但是考慮到實(shí)驗(yàn)裝置的簡陋性,及實(shí)驗(yàn)測量時(shí)存在不可避免的系統(tǒng)誤差和人為的讀數(shù)誤差等因素,此結(jié)果還是比較滿意的.因此運(yùn)用平凸透鏡與平面玻璃鏡組合的裝置測量倏逝波貫穿深度的方法是可行的.
4 關(guān)于誤差的討論
由式(14)~(17)可得到第k級(jí)暗環(huán)數(shù)據(jù)求出的貫穿深度d的表達(dá)式,忽略二階小量有:

因此用相差m級(jí)的暗環(huán)半徑求出的貫穿深度的偏差Δdm為
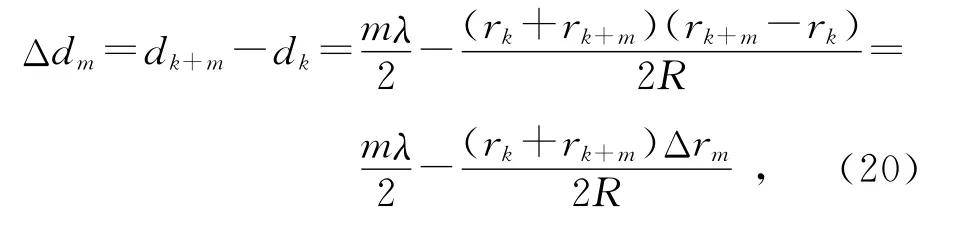
由于前幾級(jí)暗環(huán)寬度較大,測量半徑誤差較大,因此實(shí)驗(yàn)中采用了第10~20級(jí)的暗環(huán)半徑進(jìn)行計(jì)算.式(20)中,Δrm是k+m級(jí)暗環(huán)與k級(jí)暗環(huán)的半徑差值,可以用來表示暗環(huán)半徑測量時(shí)存在的讀數(shù)誤差;R表示平凸透鏡的曲率半徑,經(jīng)測量為1.496m;λ為實(shí)驗(yàn)所用鈉光燈的波長,取為589.3nm.運(yùn)用式(20)可以算出用11~20級(jí)暗環(huán)半徑求出的貫穿深度相對(duì)于用第10級(jí)暗環(huán)半徑求出的貫穿深度的偏差Δdm,如表2所示.
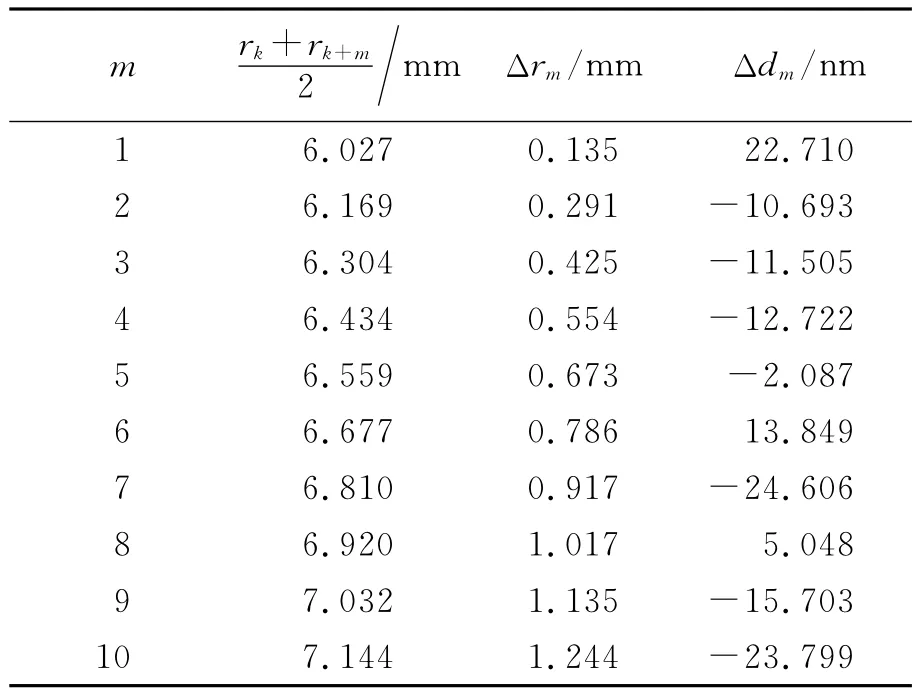
表2 用11~20級(jí)暗環(huán)半徑相對(duì)于用第10級(jí)暗環(huán)半徑求出的貫穿深度的偏差
雖然用11~20級(jí)暗環(huán)半徑求出的貫穿深度相對(duì)于用第10級(jí)暗環(huán)半徑求出的貫穿深度都存在偏差,但是偏差均較小,在可接受范圍內(nèi),而且正負(fù)均存在,充分說明誤差存在的合理性.因此也證明了此種測量方法的正確性與可行性.
5 結(jié)束語
利用平凸透鏡與平面玻璃鏡的組合裝置,在實(shí)驗(yàn)室條件下測量了倏逝波的貫穿深度,雖然結(jié)果誤差相對(duì)較大,但是作為一般實(shí)驗(yàn)室的結(jié)果還是可以接受的.因此運(yùn)用平凸透鏡、平面玻璃鏡組合裝置與等厚干涉實(shí)驗(yàn)相結(jié)合測量倏逝波貫穿深度的方法可行,該方法也可測量其他微小間距.
[1]梁銓廷.物理光學(xué)[M].北京:電子工業(yè)出版社,1982:33-35.
[2]鐘錫華.現(xiàn)代光學(xué)基礎(chǔ)[M].北京:北京大學(xué)出版社,2003:135-139.
[3]You Yizhuang,Wang Xiaohan.A new method to demonstrate frustratedtotal internal reflection in the visible band[J].Am.J.Phys.,2008,76(3):224-228.
[4]趙凱華.新概念物理教程·光學(xué)[M].北京:高等教育出版社,2004:288-289.
[5]郭碩鴻.電動(dòng)力學(xué)[M].北京:高等教育出版社,2008:24-28.
[6]萬春華.大學(xué)物理實(shí)驗(yàn)[M].南京:南京大學(xué)出版社,1994:272-277.

