基于EKF的自動泊車系統位姿估計算法設計
羅 勇,陳 慧
(同濟大學 汽車學院,上海 201804)
隨著我國汽車保有量逐年上升,路邊停車位、車庫等資源變得越來越緊張,增加了泊車的難度。因此,可提高安全性并能減輕駕駛員負擔的自動泊車系統受到了廣泛關注,并成為研究的熱點。
自動泊車系統大都是根據檢測出的庫位信息,規劃一條泊車軌跡,然后控制車輛跟蹤軌跡進行泊車[1-4]。因此,自動泊車中實時準確地獲得車輛當前的定位信息十分必要,可增強系統的安全性和可靠性。文獻[5]利用四輪小型機器人在室內進行試驗,基于運動學模型開發了泊車控制算法,但由于四輪機器人的機械特性和乘用車有所差別,并且室內環境相比于室外環境要理想很多,所以結果參考性不強;文獻[6]在乘用車上開發了泊車系統,其位姿估計算法用了4個ABS輪速傳感器和1個方向盤轉角傳感器,試驗中利用定位精度1 cm的差分GPS來驗證算法精度,軌跡終點誤差達到了30 cm;文獻[7]用4個輪速傳感器和1個方向盤轉角傳感器設計了位姿估計算法,并在乘用車上進行試驗,同樣針對軌跡終點的位置偏差進行討論,但并未提及參考位置的獲取方式,對結果的論證缺乏嚴謹性。
對于位姿估計算法的研究,難點在于解決誤差累積的問題。常見的精度影響因素有車輛實際參數與理論值不同(如車輪半徑、輪距等),參數的實時變化,傳感器信號噪聲等。常采用設計參數標定實驗、濾除信號噪聲、多傳感器信號融合等來減少誤差累積。
本文基于擴展卡爾曼濾波(EKF)技術,利用2個后輪輪速信號和方向盤轉角信號設計了車輛位姿估計算法。通過離線仿真及實車試驗,驗證了該算法的可行性和估計精度。
1 位姿估計算法設計
1.1 坐標系定義和運動學模型
如圖1所示,在全局坐標系xOy下,k時刻車輛的位姿信息表述為:車輛后軸中點的坐標(xk,yk),以及車輛中軸線指向車頭的方向與x軸的夾角θk。
泊車工況下,以運動學模型來近似描述車輛狀態,將系統離散化后,k時刻的位姿信息滿足
Δxk=vkT0cos θk,
(1)
Δyk=vkT0sin θk,
(2)

圖1 坐標系定義
(3)
式中 Δxk,Δyk為k時刻車輛位姿信息的增量;T0為采樣時間步長;vk為車輛后軸中點縱向速度;ωk為車輛橫擺角速度。
初始時刻起,對式(1) ~ (3)積分,可得k時刻車輛的位置(xk,yk)和航向角θk。然而,利用式(1) ~ (3)來計算車輛位姿,信號的噪聲可能會在積分運算中累積,進而影響算法的估計精度。所以,需要濾除算法中所用信號的噪聲。
1.2 卡爾曼濾波器

圖2 卡爾曼濾波器結構
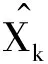
卡爾曼濾波器只適用于線性系統,當狀態方程或測量方程為非線性方程時,常使用擴展卡爾曼濾波算法。其基本思想是求非線性方程的一階Taylor展開式,忽略其余高階項,從而將非線性轉為線性,進而可將卡爾曼濾波理論應用于非線性系統中。本文基于式(1) ~ (3)設計位姿估計算法,由于方程是非線性的,需要使用EKF算法。
1.3 算法實現
卡爾曼濾波器原理設計算法,需要計算k+1時刻的系統矩陣Φk+1,k和k+1時刻的測量矩陣Hk+1。
設系統狀態向量X為
X=[x,y,θ,kl,kr]T,
式中 x、y和θ為車輛位姿信息;kl和kr為兩個后輪半徑變動系數,用來描述實際運行過程中車輪半徑的變化量。
設系統觀測向量為Z,有
Z=[v,ω]T,
式中 v為車輛后軸中點的速度;ω為車輛的橫擺角速度。

圖3 算法結構
算法的總體結構如圖3所示,輸入量為系統觀測向量Z,輸出量為車輛的位姿信息。實際應用中,觀測量v和ω的獲取方式為:取兩后輪輪速的平均值算得后軸中點的速度v;提前標定好方向盤轉角和后軸中點轉彎半徑的關系,通過查表插值的方式獲得某方向盤轉角對應的車輛后軸中點轉彎半徑R0,通過v和R0計算得到車輛橫擺角速度ω。
1)時間更新
式中f(Xk,k)為k時刻系統狀態的增量,f(Xk,k)=[Δxk,Δyk,Δθk,0,0]T。
利用k時刻左右2個后輪輪速(v3k,v4k,)和各自車輪半徑變動系數(klk,krk)來計算vk和ωk,有
vk=(klkv3k+krkv4k)/2,
(4)
ωk=(-klkv3k+krkv4k)/D,
(5)
式中 D為后輪輪距。
綜合公式(1)~(3)及(4) ~ (5),求得f(Xk,k)為
(6)
使式(6)線性化,得k+1時刻的系統矩陣Φk+1,k為
2)測量更新
k時刻,系統觀測向量Zk為
對Zk線性化后得Hk+1為
對Φk+1,k和Hk+1的計算完成之后,再根據圖2所示的算法結構進行計算,便完成了基于EKF技術的位姿估計算法的設計。
2 仿真試驗
在veDYNA中進行仿真,它是基于Matlab/Simulink平臺開發的車輛動力學模型,被廣泛應用于車輛動力學仿真等領域。
按照所用實驗車輛的參數對veDYNA車輛模型進行相應的設置:整車質量1 184 kg,軸距2.407 m,后輪距1.45 m,車輪半徑0.288 m,轉向傳動比16.3。
仿真時間為40 s,最高車速為2.5 m/s。在輪速信號中添加隨機擾動來模擬實際輪速信號的噪聲。所加的隨機擾動滿足高斯分布,其均值和標準差分別為0,0.7 r/min,運行時左后輪輪速信號如圖4所示,車輛行駛軌跡如圖5所示。
(1)地質災害高易發區(Ⅰ)。地質災害高易發區主要分布縣境內巴水河、尕干曲下游段兩岸河谷平原區以及賽欠曲兩岸低山丘陵區、黃河沿岸一帶中高山區,總面積760.51 km2,占總面積的15.18%,該區地貌單元主要為河谷沖積帶狀平原、低山丘陵區和中高山區。區內共發育地質災害點199個,泥石流災害最為發育,共計116條,其次為滑坡65處,不穩定斜坡18段。

圖4 左后輪輪速信號波形 圖5 車輛行駛軌跡
車輛行駛了26.26 m,位置誤差結果如圖6所示。本文所設計的算法在x和y方向上的最大估計偏差分別3.76 cm和2.03 cm,此精度的估計結果對于自動泊車系統的開發具有實際應用價值。

圖6 位置誤差
3 實車試驗
3.1 試驗方案介紹

圖7 春暉2號電動汽車
圖7所示為同濟大學汽車學院“春暉2號”分布式四輪驅動電動汽車,以它為平臺進行實車試驗。
使用MicroAutoBox快速原型控制器采集傳感器數據以及運行估計算法。用RT3002型GPS/INS導航儀采集車輛位置和航向角信息作為參考值,并與算法估計的結果對比,以驗證算法的精度。導航儀的位置精度為:2 cm(1σ),航向角精度為0.1(°)(1σ)。
3.2 直線行駛工況
試驗中,車輛沿直線行駛,如圖8所示,對比GPS所測行駛軌跡和算法估計的行駛軌跡。x和y方向上的偏差分別如圖9所示。車輛行駛12.22 m,位置估計的最大誤差在x方向為6.31 cm,y方向為2.74 cm。

圖8 行駛軌跡 圖9 位置誤差
3.3 圓弧軌跡行駛工況
在行駛過程中,保持方向盤轉角為-178°。對比GPS所測車輛行駛軌跡和算法估計得到的行駛軌跡,如圖10所示。x和y方向的偏差分別如圖11所示。車輛行駛距離13.53 m,位置最大誤差x方向為5.02 cm,y方向為4.77 cm。

圖10 行駛軌跡 圖11 位置誤差
3.4 泊車工況
3.5 試驗小結
算法估計得到的車輛直線、圓弧和泊車軌跡均能與GPS所測車輛實際軌跡保持較高的一致性,尤其是沿直線和圓弧軌跡行駛的時候。算法估計得到的車輛位姿信息,可以為自動泊車系統提供車輛的軌跡信息,為增強泊車安全性奠定了基礎。

圖12 行駛軌跡 圖13 位置誤差
4 結論
基于擴展卡爾曼濾波技術設計了一套自動泊車系統位姿估計算法,算法用到了兩個后輪輪速傳感器及方向盤轉角傳感器。仿真和實車試驗的結果表明,算法具有可行性,且位置估計的最大誤差控制在3%的范圍內,換言之,車輛行駛10 m,x和y方向上最大位置估計誤差在30 cm之內。本文提出的算法可以為自動泊車系統提供車輛軌跡信息的支持,為增強泊車安全性奠定了基礎。
參考文獻:
[1]吳鍇.智能自動泊車系統研究[D].南京: 南京理工大學, 2008.
[2]久保田有一, 巖切英之, 巖崎克彥,等.用于車輛的停車輔助裝置及停車輔助方法:中國, CN100535598C[P].2009-09-09.
[3]Sven Chlosta, Michael Dr Rohlfs. Method and Device for Parking a Motor Vehicle:Germany, EP1561673A2[P].2005-08-10.
[5]Kooktae Lee, Dalhyung Kim, Woojin Chung, et al. Car Parking Control Using a Trajectory Tracking Controller[C]//International Joint Conference.Busan: SICE-ICASE,2006.
[6]Kochem M, Wagner N, Hamann, et al. Data Fusion for Precise Dead Reckoning of Passenger Cars[C].Spain: IFAC, 2002.
[7]張誠, 羅勇, 陳慧. 基于擴展卡爾曼濾波算法的智能泊車航位推算研究[J].上海汽車, 2012(6):56-58,62.
[8]付夢印, 鄧志紅, 閆莉萍. Kalman濾波理論及其在導航系統中的應用[M].2版.北京:科學出版社,2010.

