軸對稱拉深成形法蘭區起皺失穩變形能及臨界壓邊力
秦泗吉 梁韶偉 張樹棟
燕山大學先進鍛壓技術與科學教育部重點實驗室,秦皇島,066004
0 引言
拉深成形工藝廣泛用于沖壓生產,起皺和破裂是成形制件的兩種主要失效形式。前者屬于壓縮失穩,后者屬于拉伸失穩。一般來說,起皺失穩問題較破裂問題復雜得多。
目前有限元分析技術已被廣泛用于板料成形過程的模擬,可以預測各種成形缺陷。而建立失穩判定條件以及判定失穩預測結果的準確性,則需要進行理論分析,并用實驗進行驗證。
塑性加工問題很復雜,一般很難采用純理論的方法進行解析求解。以軸對稱拉深成形為例,在法蘭區建立起皺失穩條件,必須先給出應力、應變以及變形能的解析表達式,其中對法蘭區應力的解析分析更是解決起皺失穩問題的關鍵,即便是在平面應力假設條件下,也很難直接給出應力的解析表達式,且無法得到應變的表達式。因此,目前常用的處理方法是:根據法蘭變形區等效應變從法蘭外緣到內緣是逐漸增大的這一規律,假設等效應變與瞬時徑向坐標成簡單的反比例關系[1-3],求出應力的解析式,然后再計算變形能,進而求出起皺失穩臨界壓邊力。
顯然,在法蘭區等效應變與位置關系成反比的假設條件與體積不變條件不一致,計算結果可能與實際相差較大。
本文以軸對稱拉深成形為例,采用能量守恒原理,對法蘭區起皺問題進行了分析。首先采用平面應變假設條件,對法蘭區的應力分布進行了分析,根據應力分布特點,以數學方法進行了簡化。然后根據徑向應力的簡化公式以及變形能隨拉深位置的變化規律,采用分部積分法,得到了起皺失穩變形能的表達式,并給出了臨界壓邊力的計算式。
1 能量法求解起皺失穩問題基本方程
板坯起皺失穩分析通常采用分叉理論[4-5]和能量守恒原理[6-7]。由于能量守恒原理更簡明且更具普遍性,故得到了廣泛應用。根據能量守恒原理,在起皺失穩瞬間,設由板坯周向伸長導致的周向應力釋放的變形能為Uθ,板坯失穩起皺時彎曲所需的變形能為Uw,由于皺紋隆起壓邊力做功為 UQ,則有如下關系[6]:

在起皺失穩瞬間,周向應力σθ釋放出的能量為[1]
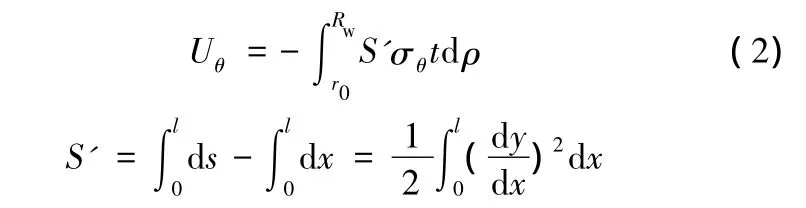
式中,S'為失穩起皺后單波的周長變化量;σθ為在任意半徑ρ處的周向應力;t為板厚;dρ為徑向坐標位置增量;r0為凹模入口處的半徑;Rw為法蘭外緣半徑;l為單個皺紋的波長;ds、dx分別為單波微弧段的弧長及其在x軸上的投影長度;y=y(x)為撓度方程。
一般情況下,將法蘭變形區皺紋模型假設為
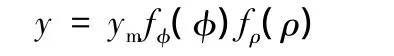
其中,ym為皺紋幅值;fρ(ρ)是與 ρ相關的函數;fφ(φ)是與φ相關的函數(φ為單波中任意弧段所對的圓心角);fρ(ρ)和 fφ(φ)是相互獨立的量綱一函數。
由 x= ρφ,dx= ρdφ,得
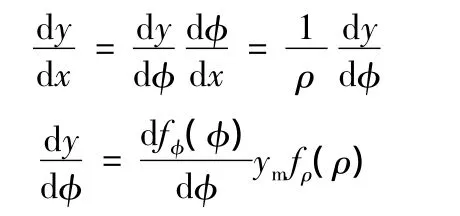
通常取[1-3]
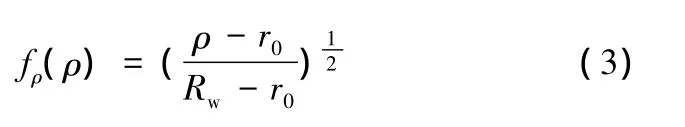
因而有
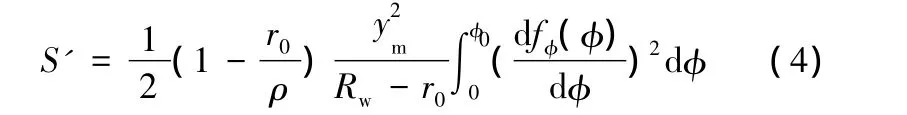
式中,φ0為單波所對的圓心角;r0為法蘭內半徑,即不考慮凹模圓角時的凹模口半徑。
將式(4)代入式(2),得
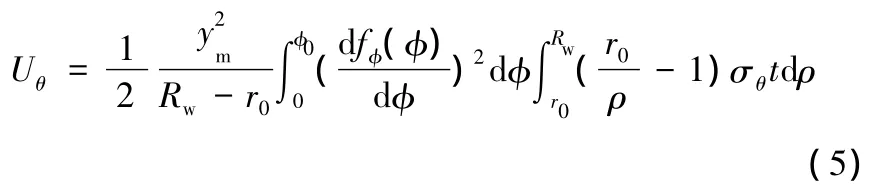
另一方面,法蘭起皺后,波紋隆起為塑性彎曲。在起皺瞬間,假設波紋撓度不大,可認為是在加載條件下發生的,并仍然滿足彈性彎曲時的小變形假設,分析計算中用塑性切線模量D替代彈性模量,波紋撓度與坐標ρ有關,因此有
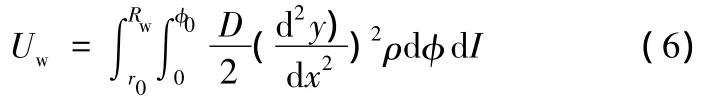
而
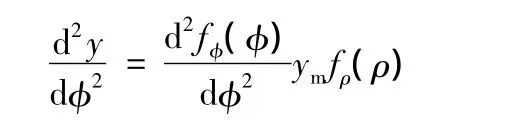
因而
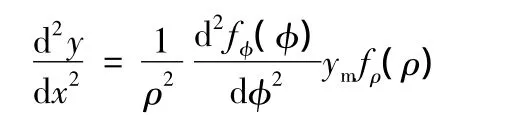
上式代入式(6),且 dI=t3dρ/12,則有
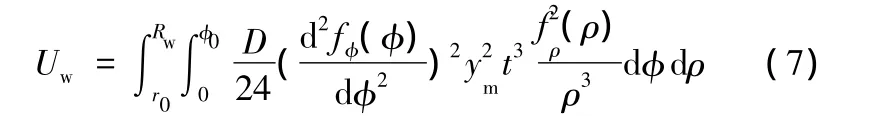
設等效應力σ與等效應變ε符合冪指數的材料模型假設,則有

式中,B為板材的強度系數;n為硬化指數。
將式(8)、式(3)代入式(7),得
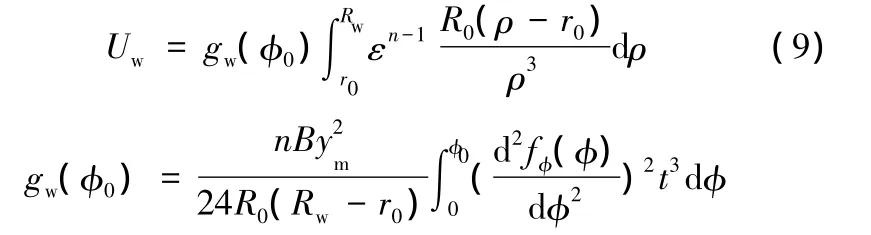
式中,R0為板坯初始半徑。
式(5)、式(9)表明,起皺失穩變形能的計算需要首先已知應力應變分布規律。對軸對稱拉深成形問題,在一定的假設條件下,可以求出應力、應變分布規律。但應力應變難以直接給出解析表達式,這使得后續工作無法進行。通常的處理方法是假設等效應變與位置關系成反比[1-3],但這種假設顯然與體積不變條件相悖。考慮在壓邊條件下,法蘭區的板厚變化不大,在求解應力分布時,許多文獻仍采用平面應變假設。以下在對法蘭區應力進行求解分析的基礎上,采用平面應變假設條件,進一步給出起皺失穩變形能、臨界壓邊力等的簡化計算方法。
2 平面應變假設條件下的應力分布
2.1 應力分析
對軸對稱拉深成形問題,法蘭區滿足的平衡方程為

式中,σρ為法蘭區徑向應力。
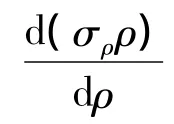
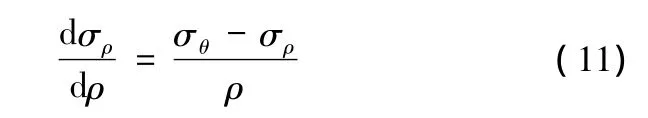
在平面應變假設條件下且不考慮摩擦等,根據式(11)及其他條件可求出法蘭區的應力[8]。
若設半徑為ρ處的變形質點的初始位置為ρ0,r為板厚方向性系數,則由等效應變的定義有

根據平面應變假設及等效應力的定義,有
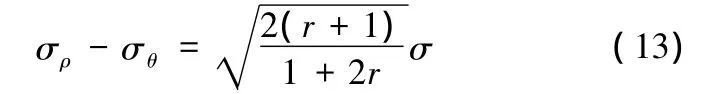
根據平面應變假設條件、Mises屈服準則及冪指數的材料模型假設,得
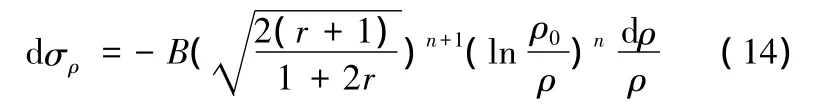
因法蘭外緣徑向應力已知,則在法蘭區任意位置ρ(ρ∈[r0,Rw])處變形質點的徑向應力為
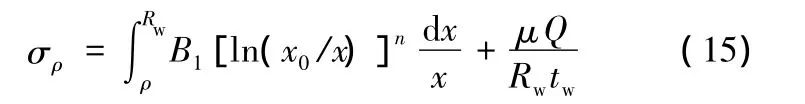
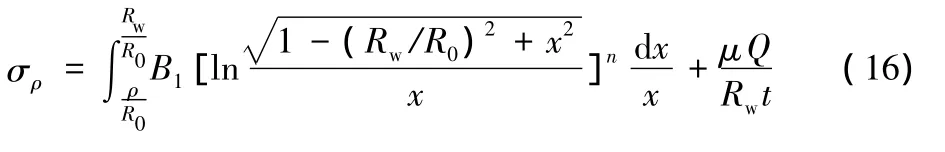
式(16)中的x表示變形質點的相對位置。
將式(16)代入式(13),并考慮等效應力等效應變關系、冪指數的材料模型假設,可求出周向應力。顯然,周向應力也是包含積分項的函數式,它是質點坐標位置的函數,再將其代入式(5),才能計算變形能Uθ,即便采用數值方法,計算過程也非常復雜。因此,將式(16)進行簡化還是非常必要的。
2.2 應力表達式的簡化
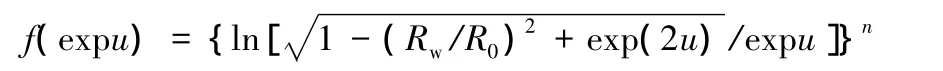
取 r0/R0=0.5,n=0.21,當 Rw/R0取不同值時,將函數f(expu)隨u的變化規律表示在圖1上。對于給定的 Rw/R0,在 u∈[ln(r0/R0),ln(Rw/R0)]內f(expu)接近線性分布。表1給出了在Rw/R0和 r0/R0取一系列不同值時,函數f(expu)線性相關系數的平方值R2。結果顯示R2均接近1。因而f(expu)在u的取值區間內線性相關密切,基本符合線性分布規律。容易驗證,當n在0.2附近變化時,上述規律不變。
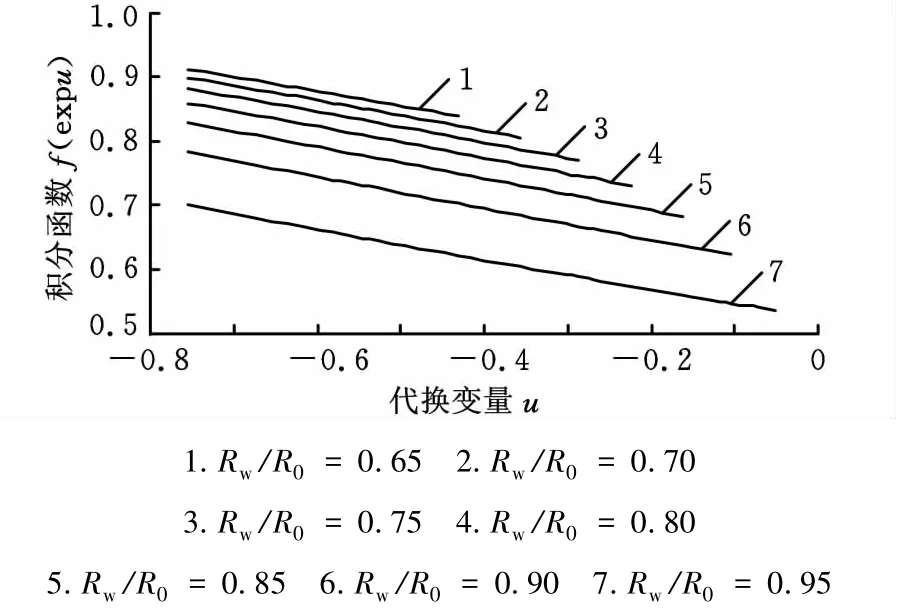
圖1 函數f(expu)隨u的變化規律
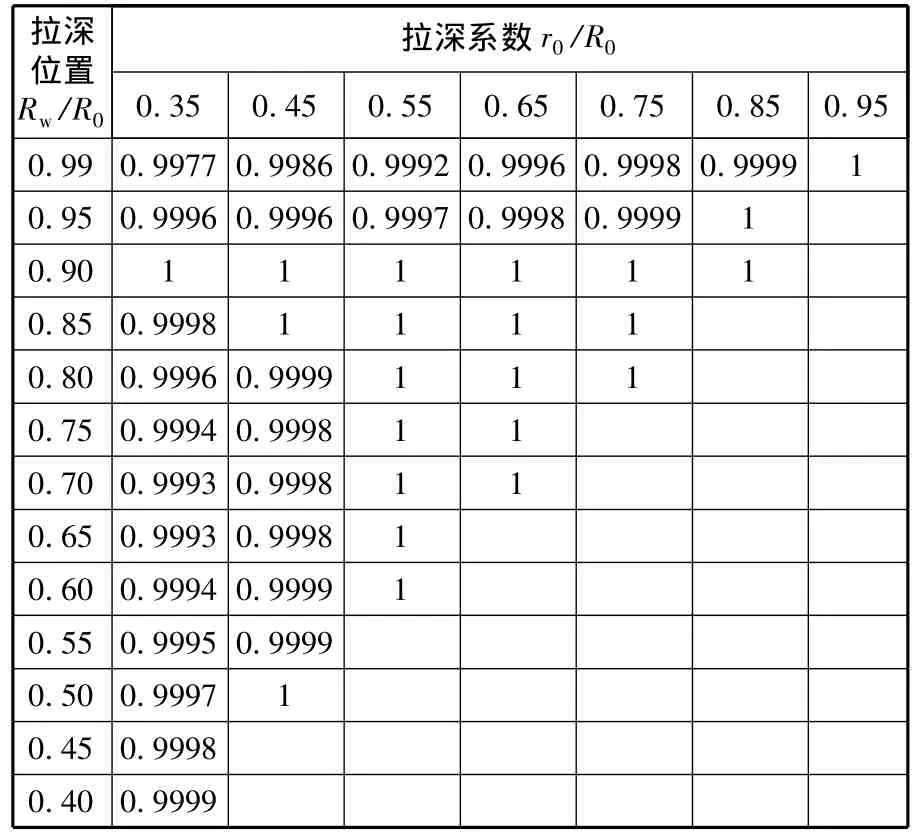
表1 函數f(expu)線性相關系數的平方值R2(n=0.21)
進行變量代換后,因積分函數近似為自變量u的線性函數,因而徑向應力可以簡化為自變量u的二次函數。參照文獻[8],以積分形式表示的應力表達式(16),采用泰勒級數展開的方法,可按下式進行簡化:
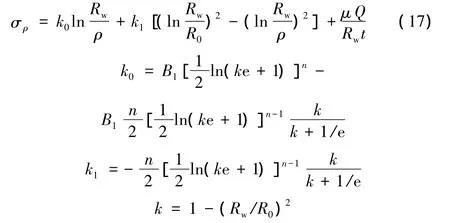
簡化后的求解結果與原積分式求解結果非常接近。文獻[8]給出的算例中,在n=0.19時,最大相對誤差小于0.6%。
只有已知應力分布規律,才能計算起皺失穩變形能,而簡明的應力表達式也為變形能的計算及進一步給出起皺失穩判據提供了便利。
3 起皺失穩變形能的計算
3.1 周向應力釋放的能
分析式(5),因σθ是ρ的函數,因而需要首先求出周向應力,才能確定周向應力釋放的變形能。
根據平衡方程式(10),式(2)可寫為
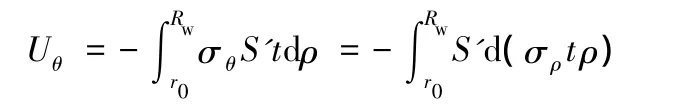
由分部積分法,得
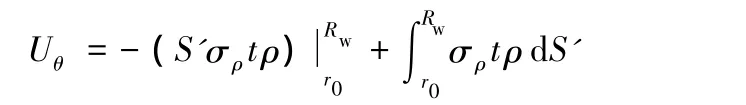
而S'可看為ρ的函數,因S'(r0)=0(法蘭凹模入口處無皺紋高度為0,因而周向伸長也為0),故可根據邊界條件,得
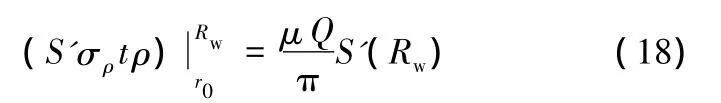
將ρ=Rw代入式(4),得
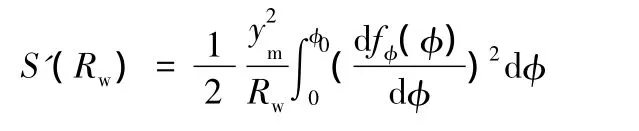
且
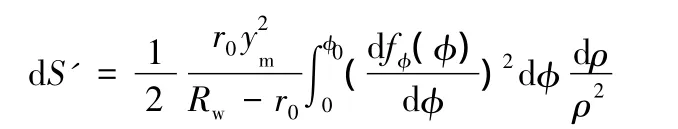
因此
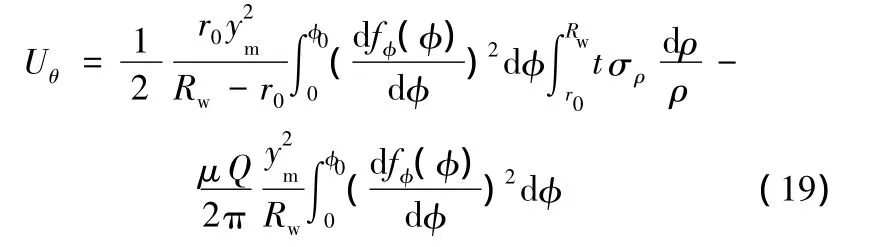
考察式(19)中的第一項,令ρ/R0=expu,由
式(17)可知,徑向應力可近似表示為u的線性函數,因此有
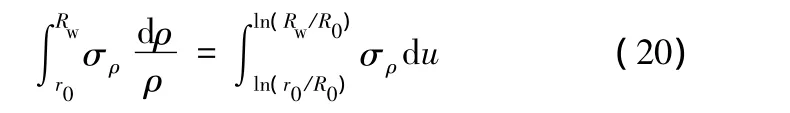
當μ=0時,若設σρ=ka+kbu+kcu2,則式(20)是可積函數,即
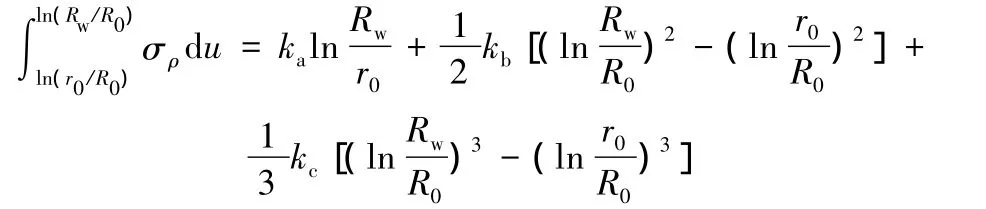
取μ =0,Rw/R0=0.85,r0/R0=0.5,n=0.21,采用式(19)(用數值方法)計算得到的結果和采用簡化式計算得到的結果非常接近,其相對誤差小于0.8%。可以驗證,當計算參數在可行范圍內變化時,誤差也很小。
若進一步設

則有
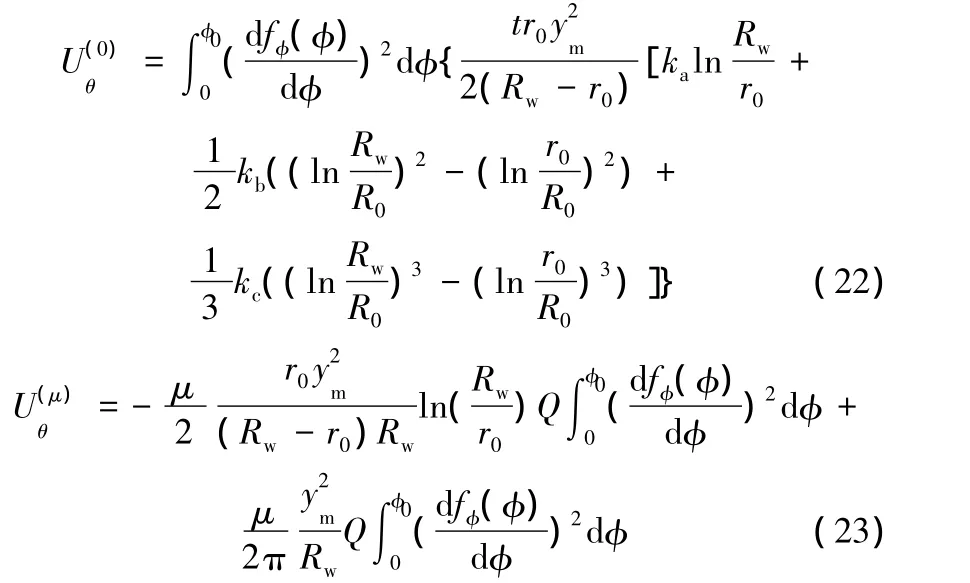
3.2 彎曲變形能
根據面積不變假設,將等效應變的表達式式(12)代入式(9),得
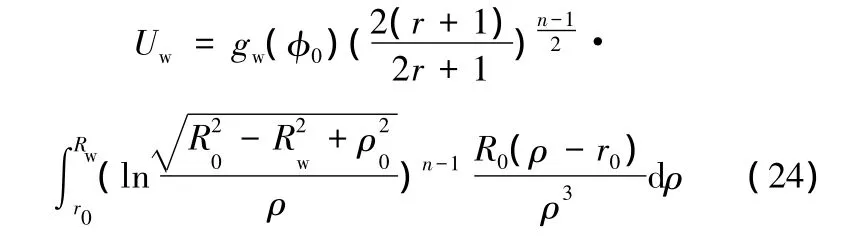
4 臨界壓邊力及理想壓邊力行程曲線
4.1 起皺失穩臨界壓邊力
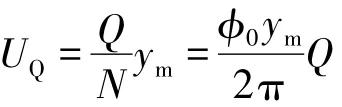
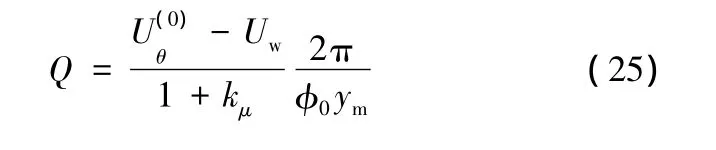
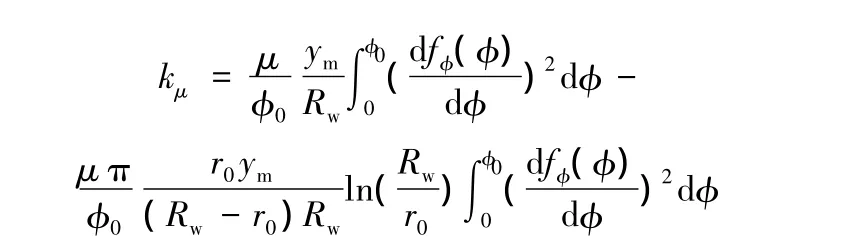
在不考慮成形速度、溫度等成形條件對起皺影響的前提下,式(25)給出了壓邊力與材料性能參數、板坯幾何參數、拉深位置參數以及皺紋模型參數之間的關系。當成形條件、材料性能參數、板坯幾何參數以及拉深位置參數一定時,壓邊力僅與皺紋模型幾何參數有關。
當其他參數一定時,壓邊力是皺紋模型參數的函數,在臨界起皺條件下,一般允許的皺紋幅值有一定的設定值,此時,壓邊力僅是皺紋數量N或單個皺紋的圓心角φ0的函數。由式(25),令壓邊力對φ0的一階偏導數為0,可得到臨界壓邊力下的φ0,將φ0再代入式(25),可以求出臨界壓邊力。可以驗證式(25)給出的Q是φ0的單凸函數,即臨界壓邊力是所有可能的壓邊力取值中的最大值。
圖2所示是當量壓邊力Q/ym(壓邊力與皺紋幅值之比)隨皺紋數量的變化曲線。可以看出,當皺紋數量為某一數值時,壓邊力達到最大值,這就是臨界壓邊力。在實際拉深過程中,當其他參數不變時,臨界壓邊力是拉深位置的函數,即壓邊力隨行程是變化的,這就是理想壓邊力行程曲線。顯然,在拉深開始和拉深結束時,臨界壓邊力都為0,而在中間的某個拉深位置,臨界壓邊力達到最大值。在拉深過程中,若保證施加的工藝壓邊力都不小于臨界壓邊力,則能確保拉深過程不產生起皺失穩。
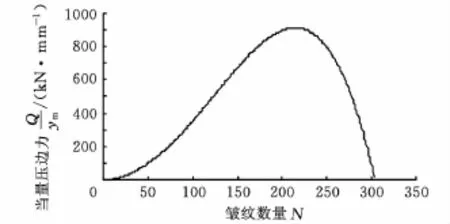
圖2 Q/ym與皺紋數量的關系曲線(μ =0.08,n=0.18)
4.2 理想壓邊力行程曲線
圖3所示是臨界當量壓邊力Q/ym與拉深位置Rw/R0(法蘭外緣的相對位置)的關系曲線,由于拉深位置與拉深行程有一一對應關系,因此該曲線是理想壓邊力行程曲線的另一種表達形式。
5 結論
(1)在平面應變假設條件下,分析了軸對稱拉深成形起皺失穩條件下的變形能,導出了計算式。
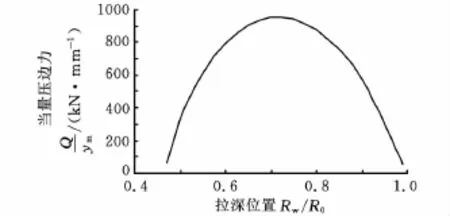
圖3 Q/ym與拉深位置的關系曲線(μ=0,n=0.18)
(2)用分部積分法、泰勒級數等數學方法簡化了變形能的計算式。新的計算式更簡明實用,與原積分形式表示的計算式非常接近。給出的算例表明,相對誤差小于0.8%。
(3)分析了起皺失穩臨界壓邊力和理想壓邊力行程曲線的含義,并給出了算例。
[1]梁炳文,胡世光.板料成形塑性理論[M].北京:機械工業出版社,1987.
[2]趙軍,張雙杰,曹宏強,等.拉深過程智能化控制中的法蘭起皺臨界條件[J].燕山大學學報,1998,22(3):197-201.Zhao Jun,Zhang Shuangjie,Cao Hongqiang,et al.Critical Flange Wrinkle Condition in Intelligent Control of Deep Drawing Process[J].Journal of Yanshan University,1998,22(3):197-201.
[3]羅亞軍.板材拉深成形變壓邊力理論和數值模擬[D].上海:上海交通大學,2003.
[4]Hill R.A General Theory of Uniqueness and Stability in Elastic/Plastic Solids[J].Journal of the Mechanics and Physics of Solids,1958,6:236-249.
[5]Hutchinson J W.Plastic Buckling[J].Advances in Applied Mechanics,1974,14:67-144.
[6]Senior B W.Flange Wrinkling in Deep-drawing Operations[J].Journal of the Mechanics and Physics of Solids,1956,48:235-246.
[7]Yu T X,Johnson W.The Buckling of Annular Plates in Relation to Deep Drawing Process[J].International Journal of Mechanical Sciences,1982,24(3):175-188.
[8]秦泗吉.軸對稱拉深成形凸緣變形區應力的解析求解[J].機械工程學報,2011,47(24):20-25.Qin Siji.Analytical Solution of Stress in Flange Deformation in Axisymmetrical Deep Drawing Process[J].Journal of Mechanical Engineering,2011,47(4):21-25.

