空間彎管仿真與回彈補償

熊威甘忠

西北工業大學現代設計與集成制造技術教育部重點實驗室，西安，710072

0 引言

作為一種重要的承載和輸送氣體、液體的輕質結構件，金屬彎管零件在高科技領域(如航空航天、造船、汽車、能源和醫療)得到了越來越多的關注［1-2］。為了將管材彎成具有一定彎曲半徑、角度和形狀的零件，彎管工藝作為管材塑性成形的重要分支，是生產輕質結構的一種十分重要的制造技術［1，3］。

以前的彎管研究主要集中在平面彎管領域，而對空間彎管(在彎曲段中，管材軸線的撓率不恒等于零的管彎零件)較少涉及。近年來，土木工程和交通系統中對三維彎曲鋼鋁構件的需求日趨強烈，空間彎管因其在空間和流體力學上的優勢，為設計者提供了新的選擇［4］。例如美國設計生產的太陽能STERLING發電機中散熱管系中的管型，管材軸線即為空間曲線［5］。文獻［6］提出了一種自由彎曲方法(free－bending)，該方法將管材擠過一個可以在兩個垂直方向偏轉的彎曲模腔，幾乎能夠成形任意外形的彎管，但是彎曲半徑要是管材半徑的2.5倍，并且對材料參數的變化較為敏感。另一種新的空間彎管方法［4，7］是扭矩疊加空間彎曲工藝(torque superposed spatial bending)，它基于滾彎工藝，通過動態調整彎曲外形和施加扭矩，來達到彎曲不同半徑和角度的目的。

一般而言，彎管成形的主要缺陷有失穩起皺、壁厚過度減薄、截面畸變、拉裂和回彈［8-9］。目前，對空間彎管的研究主要集中在對小直徑管材的彎曲研究上［5-6，10］。相對于管材的破裂起皺和截面畸變，管材的回彈是主要的成形缺陷［10］。在平面彎管的研究中，如果使用理想彈塑性模型，并且假設在彎曲過程中管徑保持不變，回彈可以使用彎曲梁理論進行計算［11-12］。但因為忽略了三維應力應變，故純解析計算結果會和試驗結果相差較大［1］，所以有限元分析成為彎管回彈的主要方法。在空間彎管的回彈研究方面，文獻［5］將管材的空間軸線離散為若干段圓弧，并通過純彎曲試驗確定每段圓弧在回彈前的半徑，最終在UG軟件中拼接各段圓弧，得到繞彎模具型面。實質上是將空間彎曲用若干個密切平面上的平面彎曲近似處理。文獻［10］發展了上述平面化的補償方法，將空間軸線分段投影到密切平面和從切平面上，同樣使用純彎曲試驗確定每段圓弧在回彈后的半徑，再將對應的一對投影圓弧在空間中合成一段空間曲線，同樣使用UG拼合，預測了空間彎管回彈后的形狀。上述文獻中沒有論述平面化回彈預測和補償的數學依據，并且沒有涉及空間繞彎的數值仿真問題。

本文通過有限元仿真研究小直徑空間彎管的回彈問題。提出了一種具有數學依據的空間彎管回彈補償方法。

1 空間彎管數值模擬

1.1 有限元模型

空間彎管使用繞彎的成形方法，繞彎模具的幾何模型(見圖1)，是沿初始截面和終止截面之間的脊線放樣而成的。兩個截面分別位于XOY面和YOZ面上;脊線是一段空間曲線，起點為rs(0)=(x0，H －rm，0)，終點的Y坐標比起點的Y坐標小H，曲線的參數方程為

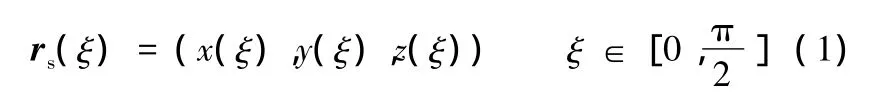
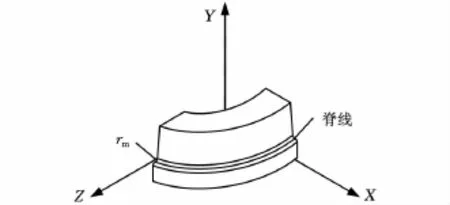
圖1 模具的幾何模型

空間彎管的有限元模型見圖2，管材使用C3D8R網格，管材外半徑rp=2.8mm，略小于型面半徑rm=3.0mm，這是因為將模具型面的截面半徑同管材半徑設為一致，在進行網格劃分時，兩者的網格有可能相互干涉而導致分析失敗。管材的內徑為5.0mm，材料為鋼材，使用線性強化模型，設定彈性模量為210GPa，泊松比為0.33，屈服應力σy=418MPa，硬化系數Hp=31 579GPa。模具和壓板的彈性模量比管材的彈性模量大一個數量級，以保證在成形過程中不發生過大的變形。

壓板是內徑為6mm、厚1mm、旋轉角為90°的環扇形，參考點設在圓心。壓板比管材略長，這是出于有限元分析收斂性的考慮，長的壓板可以控制自由端，防止產生不確定的運動，使成形過程為準靜態。

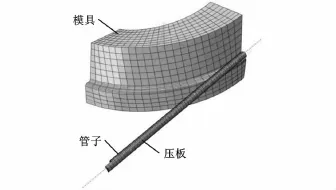
圖2 空間彎管有限元模型

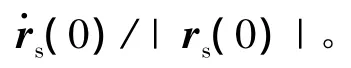
模型使用ABAQUS/Standard求解，只設定一個分析步，時間為2s，在前一秒中壓板參考點沿軌跡從XOY面運動到YOZ面，對管材加載;后一秒，壓板參考點沿原路徑返回XOY面，完成卸載。

1.2 用戶幅值子程序

空間彎管使用繞彎的方式成形時，需要控制壓板沿空間曲線運動，在彎管的過程中，壓板的6個自由度需要相互協調運動，都是時間的函數。在ABAQUS中，需要使用用戶幅值子程序(UAMP)來實現。在UAMP程序的接口中需要關注如下幾個形參變量:

(1)ampName，用戶指定的幅值名稱，用于區分當前幅值所賦給的自由度。

(2)time，由當前分析步所完成的時間和全部分析步所完成時間組成的數組。因為模型中只設一個分析步，兩個時間相等，所以統一記作t，用于判定加載和卸載。

(3)ampValueOld，記作tA，增量步開始時刻的幅值。

(4)ampValueNew，記作t+ΔtA，增量步結束時刻的幅值。

(5)dt，記作 Δt，時間增量。

根據壓板和模具的裝配關系，在加載過程中，壓板參考點的運動軌跡為

幅值tA 有 6 個分量tAi，i=1，2，…，6，相應的t+ΔtA 也有6 個分量，為t+ΔtAi，i=1，2，…，6，其中前3個分量分別表示沿X、Y、Z軸的平動位移，后3個分量表示繞相應坐標軸的轉動。

對于移動分量t+ΔtAi(i=1，2，3)，有

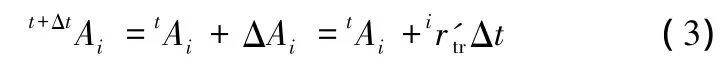
式中，irtr表示位置向量rtr的第i個分量。

對于轉動分量t+ΔtAi(i=4，5，6)，有

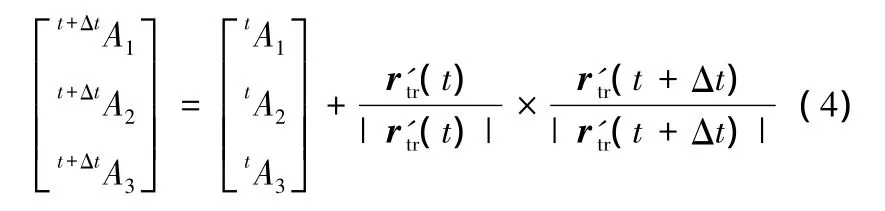
在卸載的過程中壓板參考點的運動軌跡為

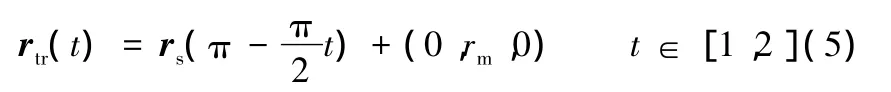
同樣可以使用式(3)和式(4)計算t+ΔtA。

1.3 仿真試驗設計

在空間曲線局部建立Frenet標架，曲線同時具有曲率和撓率，在研究平面彎曲變形時，常使用純彎曲試驗(曲率為固定值)。對比這種做法，將模具的脊線設計為圓柱螺線(圖3)，即

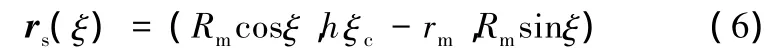
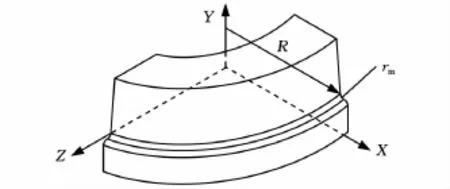
圖3 圓柱螺線模具

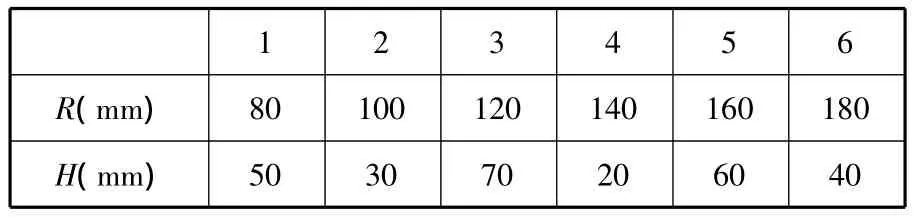
表1 均勻設計因素及水平

圓柱螺線的曲率κ和撓率τ均為固定值，分別為

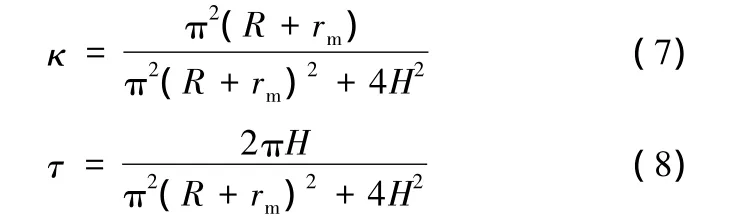
使用U6(6d)均勻設計表設計仿真試驗，水平順序見表1。

2 仿真數據處理

2.1 中心線提取

在研究管材的回彈問題時，為了便于描述管子的空間形狀變化，可以以管子的中心線作為研究對象，因為根據彎曲理論，圓管的中心線位于彎曲的中心層上，可以認為長度不變。但是管子的中心軸線不是一個幾何實體，在ABAQUS中不能設定Set集合，無法提取出節點坐標。可以提取出的節點坐標是管壁上的網格節點，所以需要根據管壁上的節點坐標計算出截面中心點的坐標，即進行中心線提取。目前關于中心線提取的研究［13-15］多是關于從CT圖像中提取血管的中心線，關于空間節點集的中心線提取沒有查獲相關的算法，為此需要設計相應的算法。

管子外表面的部分節點如圖4所示。要處理的節點在空間位置上有一定的分布規律，近似沿若干個截平面分布;相鄰兩個截平面之間的距離大體相同，后一個截平面相對于前一個截平面既有移動又有轉動，移動距離大體相同，但是轉動角度和方向未知;數據的有效位數有限，如果只采用少數點進行計算會帶來較大的誤差。由于在仿真的過程中，管子的一端是固定的，所以以固定端作為提取中心點的初始位置，初始位置的中心點是可以估算的。

圖4 管子外表面節點

本文根據以上分析提出了一種中心線提取方法，基本思路如下:以前一個截面的中心點為球心，建立半徑為r的球面，沿截面的法向量方向移動球面直到和下一個截面的節點接觸為止，根據初步接觸點擬合平面，查找在平面附近的節點，再次擬合平面，這個平面就是新球面的大圓截面，可以算出圓心點和截面的法線方向。具體算法流程如下。

(1)初始化。給定擬合誤差限ε，給定終止計算時的節點個數NT，給定球心點C(0)、半徑r和大圓截面初始法向量V(0)，設定試探移動步長h，次數k=0，擴張系數為λ。

(2)計算節點集中包含點的個數N(k)，如果N(k)＜ NT，停機，C(i)(i=0，1，…，k)即為要提取的截面中心點。

(3)設定試探球心Ct=C(k)，半徑r?R，前球心 CF=C(k)+hV(k)，后球心 CB=C(k)－ hV(k)。

(4)計算點集中節點到球心的距離dj(j=1，2，…，N(k))，統計在球面內點的個數mI和落在球面上點的個數mO。

(5)如果 mI＞ 0，則令 CF=Ct，Ct=(CF+CB)/2，轉步驟(4)。

(6)如果 mO=0，則令 CB=Ct，Ct=(CF+CB)/2，轉步驟(4)。

(7)如果 mO＜ 3，λ R?R，否則，轉步驟(9)。

(8)查找落在球面上點的個數mO，轉步驟(7)。

(9)使用落在球面上的點擬合平面Pt，方向設為V(k+1)，V(k+1)和V(k)的夾角小于π，并計算節點集中的點到平面Pt的有向距離，查找所有距離小于ε的點，構成截面點集。

(10)使用截面點集擬合半徑為r的球面，球面圓心設為C(k+1)。

(11)k+1?k，轉步驟(2)。

完成中心點的提取后，令s0=0，對于C(i)(i=1，2，…，k)，使用 si=si－1+|C(i)－ C(i－1)| 作為參數，將 C(i)(i=1，2，…，k)3個方向上的分量分別對si擬合三次函數，得到中心線的參數方程r(s)。

2.2 仿真結果分析

中心線參數方程的曲率κ(s)和撓率τ(s)分別為

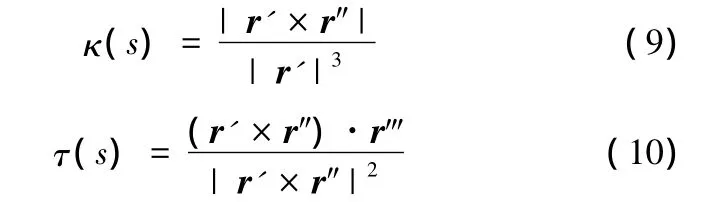
相應的模具的曲率和撓率可以按式(7)和式(8)計算。

建立回彈前后曲率、撓率的對應關系，如圖5所示。可以發現兩組數據在試驗范圍內都接近于線性關系。

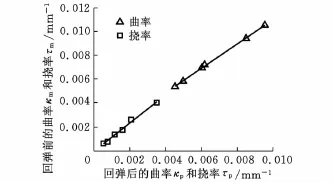
圖5 回彈前后曲率、撓率關系

分別擬合回彈前后曲率、撓率，得

式中，κp、τp分別為回彈后的曲率和撓率，mm－1;κm、τm為回彈前的曲率和撓率，mm－1。

3 回彈補償

3.1 補償算法

根據式(11)和式(12)可計算出目標曲線上的每一點在模具脊線上對應點的曲率和撓率。相當于模具脊線上每一點的曲率κm和撓率τm都是已知的。從微分幾何的角度考慮，對于在空間中不含逗留點的兩條曲線，如果能夠適當地選擇公共自然參數s，使得在對應點兩條曲線有相同的曲率和撓率，那么兩條曲線是可以通過一個空間剛體運動相互重合的。所以，如果不考慮空間位置的差異，根據目標曲線可以唯一地計算出一條模具脊線。

由曲率和撓率求解空間曲線方程實際上是自然方程的積分問題，即首先求解Frenet－Serret方程:

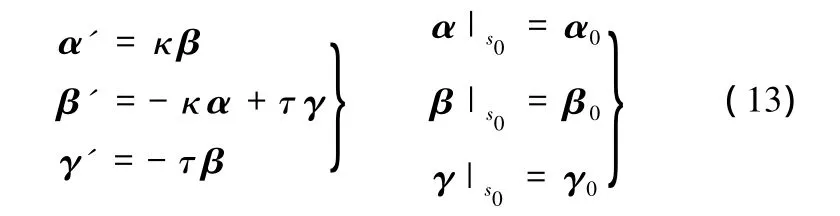
其中，α為單位切向量，β為單位主法向量，γ為單位副法向量，它們構成曲線上某點的基本三棱形。

得到α、β、γ后再求解微分方程:

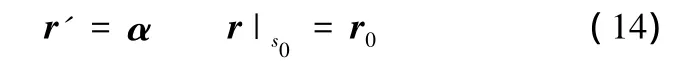
考慮到簡化UAMP子程序編寫的需求，在此使用一種半數值的補償方法。另外，因為在定義曲線時，為了直觀起見使用的是一般參數，故需要進行參數轉化才能使用上述公式。具體的補償過程如下。

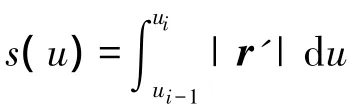
(2)初始化。計算目標曲線的初始位置rp(0)，以及在初始位置的三棱標架 α0=r'p(0)，β0=α'0/|α'0|，γ0=α0× β0作為方程(13)和方程(14)的邊界條件。

(3)求解Frenet－Serret方程組。將區間［0，sm］等距劃分，使用四階Runge－Kutta方法求解方程(13)，得到一系列αi的值。

(4)擬合切向量。使用三次多項式函數在區間［0，sm］擬合 αi，得到方程(14)的近似表達式r'=α。

(5)位置矢量積分。結合步驟(2)中的邊界條件rp(0)，對r'=α直接積分得到rm。

進一步分析上述對曲線基本公式積分的補償方法，補償只要求知道曲率和撓率方程，而和具體的成形過程和截面形狀無關。而且如果將成形后零件的曲率和撓率表示成模具曲率和撓率的函數，對自然方程積分還可以求解回彈預測問題，例如對于撓率恒等于0的情況(金屬窄條的二維彎曲［16］)，也可以使用上述方法求解，但因為不需要在三維空間中求解微分方程，補償過程可以大大簡化。

3.2 補償驗證

驗證使用的目標彎管的中心線參數方程為

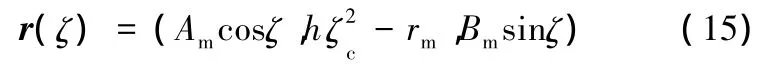
可以計算出式(15)的曲率和撓率方程:

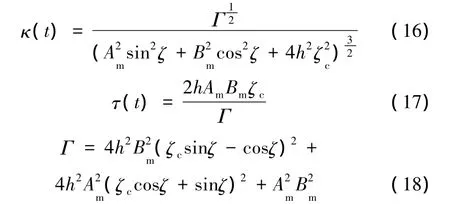
從式(16)和式(17)可以看出，目標曲線的曲率和撓率都不是固定值。先使用3.1節的方法進行補償計算，按照1.1節生成模具，建立有限元模型，按1.2節中所述的公式編寫UAMP子程序。然后進行有限元仿真，對仿真結果使用2.1節的方法提取中心點，將得到的中心點數據導入CATIA，并刪除延長段的數據點和噪點，擬合空間樣條。最后將目標曲線也導入CATIA中，如圖6所示。因為使用目標曲線的初始位置矢量和初始基本三棱形作為求解微分方程的邊界條件，所以可以認為得到的曲線和目標曲線是已經進行了粗略配準的。使用CATIA的測量功能，得到兩條曲線的距離最大值約等于4.649mm。外形基本吻合，與文獻［10］中的結果對比，在文獻［10］中，軸線在俯視方向上，最大誤差為5.15mm，由此可見，補償效果與文獻［10］處于同一水平。

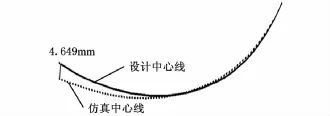
圖6 回彈補償效果檢驗

4 結論

(1)建立了空間繞彎的有限元模型，并編寫了繞彎的UAMP子程序。通過圓柱螺線型模具上的繞彎仿真試驗，建立了回彈前后曲率和撓率的函數關系。

(2)提出了一種提取管狀節點集截面中心點的方法，使用該方法從仿真結果中提取出了彎管的中心線。

(3)提出了利用空間曲線基本方程對空間彎管進行回彈補償的方法。仿真試驗證明，上述方法可以合理計算出空間繞彎模具的形狀。

［1］Yang He，Li Heng，Zhang Zhiyong，et al.Advances and Trends on Tube Bending Forming Technologies［J］.Chinese Journal of Aeronautics，2012，25:1-12.

［2］詹梅，楊合，江志強.管材彎曲成形的國內外研究現狀及發展趨勢［J］.機械科學與技術，2004，23(12):1509-1514.Zhan Mei，Yang He，Jiang Zhiqiang.State of the Art of Research on Tube Bending Process［J］.Mechanical Science and Technology，2004，23(12):1509-1514.

［3］楊合，孫志超，林艷，等.管成形技術發展基礎問題研究［J］.塑性工程學報，2001，8(2):83-85.Yang He，Sun Zhichao，Lin Yan，et al.Advanced Plastic Processing Technology and Research Progress on Tube Forming［J］.Journal of Plasticity Engineering，2001，8(2):83-85.

［4］Hermes M，Chatti S，Weinrich A，et al.Three－dimensional Bending of Profiles with Stress Superposition［J］.International Journal of Material Forming，2008，1(S1):133-136.

［5］李雁鵬，吳建軍.非平面彎管成形過程的回彈補償研究［J］.鍛壓技術，2009，34(1):89-92.Li Yanpeng，Wu Jianjun.Study on Spring－back Compensation for Non－plane Tube Bending Process［J］.Forging ＆ Stamping Technology，2009，34(1):89-92.

［6］Gantner P，Herbert B，Harrison D K，et al.Free－Bending—A New Bending Technique in the Hydroforming Process Chain［J］.Journal of Materials Processing Technology，2005，167:302-308.

［7］Chatti S，Hermes M，Tekkaya A E，et al.The New TSS Bending Process:3D Bending of Profiles with Arbitrary Cross－sections［J］.CIRP Annals－Manufacturing Technology，2010，59(1):315-318.

［8］李恒.多模具約束下薄壁管數控彎曲成形過程失穩起皺行為研究［D］.西安:西北工業大學，2007.

［9］寇永樂，楊合，詹梅，等.薄壁管數控彎曲應變的網格法研究［J］.中國機械工程，2006，16(S1):31-34.Kou Yongle，Yang He，Zhan Mei，et al.Research on Strain Distribution of Thin－walled Tube in NC Bending Process Using Grid Method［J］.China Mechanical Engineering，2006，16(S1):31-34.

［10］張深，吳建軍.空間彎管的回彈預測［J］.航空學報，2011，32(5):953-960.Zhang Shen，Wu Jianjun.Spring－back Prediction of Non－planar Tube Bending［J］.Acta Aeronautica et Astronautica Sinica，2011，32(5):953-960.

［11］Al－Qureshi H A.Elastic－plastic Analysis of Tube Bending［J］.International Journal of Machine Tools＆ Manufacture，1999，39(1):87-104.

［12］Al－Qureshi H A，Russo A.Spring－back and Residual Stresses in Bending of Thin－walled Aluminum Tubes［J］.Materials and Design，2002，23(2):217-222.

［13］王勝軍，付玲，康雁，等.一種基于管狀特征的冠脈中心線自動提取算法［J］.東北大學學報(自然科學版)，2011，32(1):27-31.Wang Shengjun，Fu Ling，Kang Yan，et al.Automatic Centerline Extraction Based on Tubular Feature for Coronary Arteries［J］.Journal of Northeastern U-niversity(Natural Science)，2011，32(1):27-31.

［14］許燕，胡廣書，商麗華，等.基于Hessian矩陣的冠狀動脈中心線的跟蹤算法［J］.清華大學學報(自然科學版)，2007，47(6):889-892.XuYan， HuGuangshu， ShangLihua， etal.Adaptive Tracking Extraction of Vessel Centerlines in Coronary Arteriograms Using Hessian Matrix［J］.J.Tsinghua Univ.(Sci.＆Tech.)，2007，47(6):889-892.

［15］李穎超，劉越，王涌天.基于多尺度Hessian矩陣和Gabor濾波的造影圖像冠脈中心線提取［J］.中國醫學影像技術，2007，23(1):133-136.Li Yingchao，Liu Yue，Wang Yongtian.Algorithm for Centerline Extraction of Coronary Arterial Tree in Coronary Angiographic Projections Based on Hessian Matrix and Gabor Filter［J］.Chin.J.Med.Imaging Technol.，2007，23(1):133-136.

［16］王曉林，周賢賓.金屬板彈塑性非圓弧彎曲回彈的計算［J］.塑性工程學報，1996，3(4):27-33.Wang Xiaolin，Zhou Xianbin.Springback Analysis of Varied Curvature Elastic－plastic Bending for Sheet Metal［J］.Journal of Plasticity Engineering，1996，3(4):27-33.