車輛導航系統中基于街區分塊的分層路網路徑規劃

張照生 楊殿閣 張德鑫 連小珉

清華大學汽車安全與節能國家重點實驗室，北京，100084

0 引言

隨著智能交通技術的不斷發展，車輛導航技術越來越廣泛地應用于駕駛輔助系統中［1-3］。路徑規劃是車輛導航技術的一個重要功能［4-5］，在目前的尋路算法中，經典的路徑規劃算法是Dijkstra算法［6］和 A* 算法［7-8］。但由于當前導航電子地圖數據龐大(350萬路口、560萬路段)，在平面路網［9］中運行Dijkstra算法或A*算法均不能滿足規劃速度的需求，另外，受嵌入式導航設備硬件條件的限制，地圖數據不能一次性讀入系統內存［10］，因此需要對地圖數據按照一定的準則進行模塊化處理，以滿足嵌入式系統計算及顯示的需要。目前針對路徑規劃的導航路網大多采用分層分塊的方法來提高數據的讀取效率并減少節點拓展數量［11-15］，傳統的地圖分塊［16］按照固定經緯度范圍劃分網格，該方法中路網密集的地方數據量過多，而路網稀疏的地方數據量過少，導致路徑規劃數據使用效率低。

本文提出一種路網分塊方法，考慮實際路網中街區路段分布特性(路網稀疏則街區面積較大，否則街區面積較小)，在不同等級路網中按照街區特性在路網中自然分塊，每個街區作為地圖中的一個塊。同時利用路徑規劃的起終點距離及所在的塊控制路網拓展等級，利用拓展半徑和鄰接塊范圍控制路網拓展范圍。最后采用路網分層方法結合街區分塊在大規模路網中實現了路徑規劃算法。

1 路網分層分塊

分層分塊路網的路徑規劃如圖1所示，在路徑規劃過程中，在起點附近盡快上升到高層路網中拓展，在高層路網中拓展到終點附近然后降級拓展，最終在底層路網拓展到終點。高層路網中路段稀疏，拓展到的節點少，與平面路網規劃算法相比，明顯提高了路徑規劃的速度。

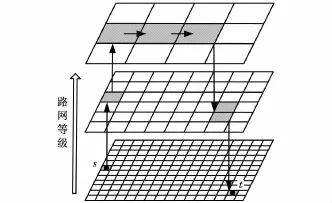
圖1 分層分塊路網路徑規劃思路圖

圖1中，路網按照路段等級分層，每層路網按街區分塊，s與t分別為路徑規劃的起點和終點，箭頭表示拓展方向，深色區域為拓展區域。

路網中路段集合E表示為

式中，i為路段等級;e(i)為路網中等級為i的路段集合;N為路網級別總數。

第i層路網中路段集合E(i)={e(j)|j≥i}。

城市路網包括骨干路網及連接骨干路網的區域路網，城市管理部門在城市規劃中已經考慮道路的分布，道路稀疏的地方區域路網面積較大，道路稠密的地方區域路網面積較小，因此不同區域路網內部道路數量相差不大。這里將區域路網做為一個街區(街區內部道路等級較低，周邊道路等級較高)，本文利用路網的街區特性，將第i層路網中形成的最小封閉區域作為第i－1層路網中的“塊”。路徑規劃升級過程中，總是由低級路網的邊界升級到高級路網，其在低層路網中的拓展過程恰好就是街區內部區域的拓展，拓展范圍與街區分塊方法一致。另外因為“塊”以高等級路網做邊界，因此與按照經緯度進行物理分塊相比，這種分塊方法不會破壞實際道路的拓撲結構，并且由于單位塊中道路數量分布均勻，路徑規劃中讀取的數據在路徑拓展中能得到較好使用，因此在數據使用過程中該分塊方法數據利用效率高。

在路徑拓展的過程中，考慮用戶的出行習慣，對于一些距離較長的路線，通常并不刻意選擇距離最短的路徑，而是盡快找到起點附近的高等級道路，通過高級路網到達終點附近后，再進入區域內部的低層次路網到達終點。這里按照路段的等級將路網分為N級，等級越高路網越稀疏，分層路網如下:

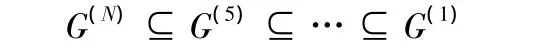
式(2)中，V(i)為第i層路網節點集合，高級路網中的元素集合從屬于低級路網元素集合，上層路網形成的最小封閉區域稱為下級路網中的“塊”，路網的分級分塊如圖2所示。

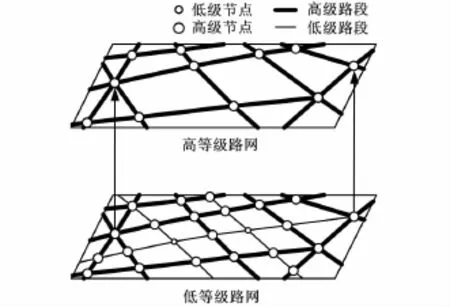
圖2 雙層路網分層分塊模型

圖2中，低等級路段(細實線)與低等級路段之間的交點為低等級節點，高等級路段(粗實線)與低等級路段的交點或高級路段之間的交點為高等級節點。高等級路段和高等級節點構成的路網為高層路網，粗實線構成的封閉區域為低層路網的“塊”。在分塊過程中，從任意一個低等級節點出發，以廣度優先原則拓展該節點，遇到高等級節點則該拓展方向停止，待最優隊列中所有節點都為高等級節點，則拓展到的節點集合為塊節點集合。

2 路徑規劃

2.1 路網拓展范圍及拓展等級

路網的拓展范圍R由起點所在的塊及起點的面積拓展范圍共同確定，表示如下:

式中，A為起點s的面積拓展范圍;B為起點s的塊拓展范圍。

面積拓展范圍A表示為

式中，r為半邊長;S為面積函數。

S(r，s)是一個以點s為中心、以r為半邊長的正方形。起點的塊拓展范圍B為

路徑規劃前，首先確定路徑的拓展等級，即路徑最高在第幾層路網中拓展，拓展等級H由路徑的距離和起終點所在的塊兩個因素確定:

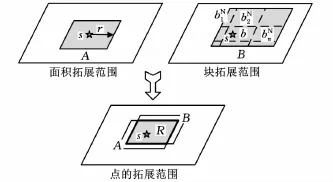
圖3 點的拓展范圍影響因素

式(6)中，hs為由距離確定的拓展等級，hb為起終點共同所在的塊確定的拓展等級，若起終點在第i級路網中同屬于一個塊，則塊拓展等級hb等于i，即

式中，b(j)為起點或終點在第j層所在的塊。

由距離確定的拓展等級hs如下:

式中，ls，t為起點和終點的直線距離;l(i)為第i層路網距離拓展閾值。

各層路網的距離拓展閾值如表1所示。

表1 各層路網的距離拓展閾值

2.2 節點拓展

路徑規劃的過程即為節點拓展的過程，拓展過程中，所有拓展到的節點都存儲在拓展節點集合U中，拓展節點集合U表示為

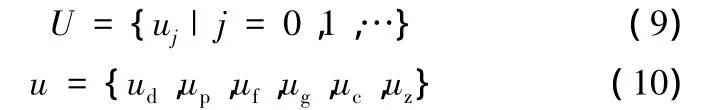
式中，uj為拓展節點;j為節點序;ud為節點ID;up為節點經緯度位置;uf為起點s經過節點u到達終點t的總代價;ug為起點s到節點u的已有最小代價;uc為節點顏色;uz為節點u的父節點在拓展節點集合U中的節點序，起點s對應節點的父節點序為 －1。

節點顏色uc的表達式為

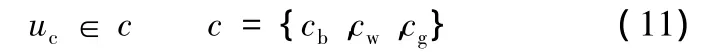
式(11)中，cb(黑色)表示已經拓展節點;cw(白色)表示未拓展節點，cg(灰色)表示正在拓展節點。在路徑拓展的過程中，黑色節點不可以向外拓展也不可以被拓展，灰色節點可以向灰色節點或白色節點拓展，白色節點只能被拓展。

拓展規則如圖4所示。

已有代價ug的計算式為

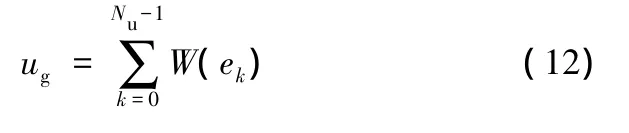
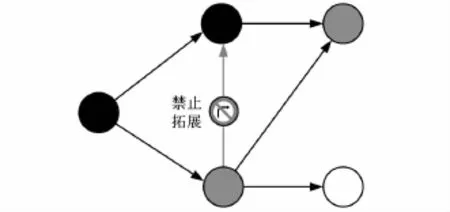
圖4 節點拓展規則

式中，Nu為從起點s到節點u所經過的路段條數;k為路段序號;W(ek)為路段ek的代價。

總代價uf為已有代價ug和啟發代價uh之和，即

啟發代價uh為節點u到達終點t的預估代價，其計算公式為

式中，eu，t為節點u與終點t兩點連線形成的虛擬路段。

路徑規劃中灰色拓展節點的節點序存儲在拓展隊列Q中，如下所示:

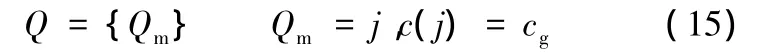
拓展隊列中節點序Qm按照該節點的總代價由小到大順序排列，c(j)是節點序號為j的節點顏色。

拓展到的白色節點加入到拓展節點集合U中，其節點序加入到拓展隊列Q中，且節點顏色變為灰色。拓展隊列中的灰節點若再次被拓展到，將本次拓展得到的已有代價ug與上次拓展已有代價u'g比較，若ug較小，則本次的拓展數據替換上次的拓展數據，表達式為

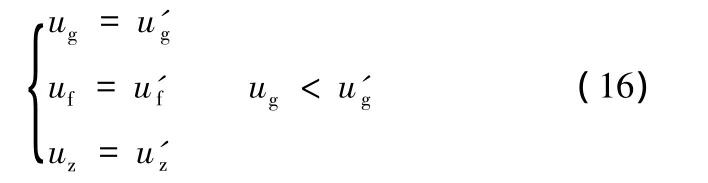
在路徑拓展的過程中，考慮人們的出行習慣，對于一些距離較長的路線，通常是盡快找到起點附近的高等級道路，這就需要節點的升級拓展，節點的升級拓展需要滿足3個條件:①有上級節點;②當前路網級別不是最高拓展等級;③上級節點在拓展范圍內。

以第一級和第二級路網為例，節點的升級如圖5所示。節點u(1)的上層節點u(2)不在拓展區域內，則該節點不能升級拓展。

2.3 最優路生成

最優路的拓展結束需滿足以下條件:①待拓展節點與終點t對應節點重合;②拓展隊列為空。其中條件①表示搜索得到最優路徑，條件②表示從起點s到終點t無最優路徑。拓展終止條件為

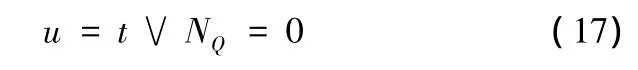
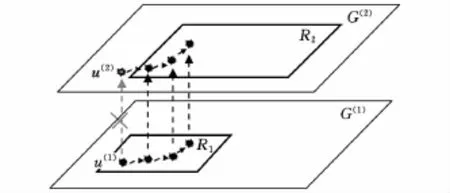
圖5 節點的升級拓展

式中，NQ為拓展隊列Q中節點個數;“∨”表示邏輯“或”。

路網拓展結束后，會得到一顆拓撲樹，對拓撲樹進行回溯，就會得到最優路路徑節點的序列。節點回溯如圖6所示。

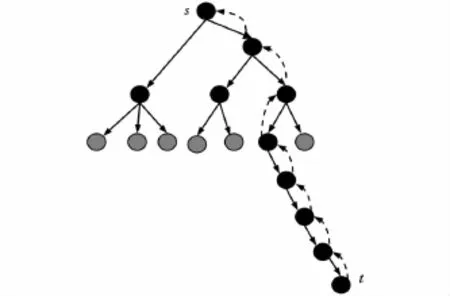
圖6 最優路節點回溯

如圖6所示，實線箭頭表示節點的拓撲方向，虛線箭頭表示節點回溯方向。回溯時根據節點的父節點序號從節點數組循環查找父節點，當父節點序號為 －1(起點s父節點序號為－1)時，終止循環。節點回溯可以找到最優路徑節點集合，將這些節點順次連接起來，就生成了最優拓撲節點路徑，如圖7所示。

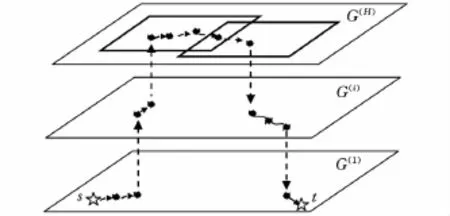
圖7 最優拓撲路徑

3 試驗驗證

本文所有試驗在嵌入式平臺上完成，試驗平臺為主頻500MHz的ARM處理器，內存128MB;實驗路網選用全國路網，路網中路口個數為3 479 368，路段數為5 643 890，算法用 Visual C++編程實現。

路網按照路段級別共分為6層，路網中路段級別與類型如表2所示。

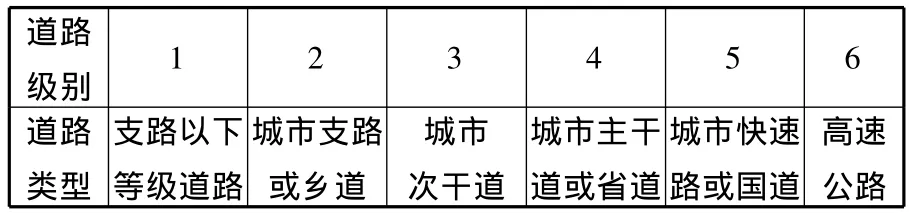
表2 路網中道路級別與分類

在分層路網中，采用街區分塊的方法，在路網密度較大的北京市路網進行了短距離尋路，起點設在北京市清華大學，終點設在北京市通州區西太平莊，將平面路網規劃和分層路網方法進行比較，規劃效果如圖8所示。

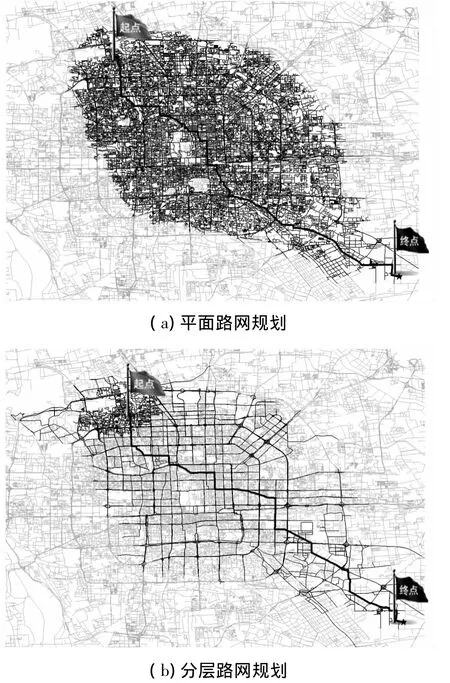
圖8 局域路網中分層路網拓展區域與單層路網拓展區域比較

如圖8所示，圖中黑色粗實線為最優路，黑色細實線為拓展到的道路，灰色細實線為未拓展的道路。圖8中，平面路網規劃拓展節點數為234 067，分層路網規劃拓展節點數為29 684，由此可以看出，分層路網規劃與平面路網規劃相比，拓展點數大大減少。另外，本文對廣域路網中長距離規劃做了對比，規劃起點設在山西省太原火車站，終點設在四川省成都市萬隆花園，平面路網規劃拓展節點數為346 843，分層路網規劃拓展節點數為18 625，規劃對比結果如圖9所示。

從圖9可以看出，在長距離規劃中，與平面路網規劃相比，其規劃拓展的節點更少，從而可以獲得更大的加速比。在路網中選擇不同位置的起點與終點進行了大量實驗，計算分層路網情況下的規劃時間，并與平面路網規劃時間對比，計算路網分層對路徑規劃效率的影響，計算結果如表3所示。

圖9 廣域路網中分層路網拓展區域與單層路網拓展區域比較

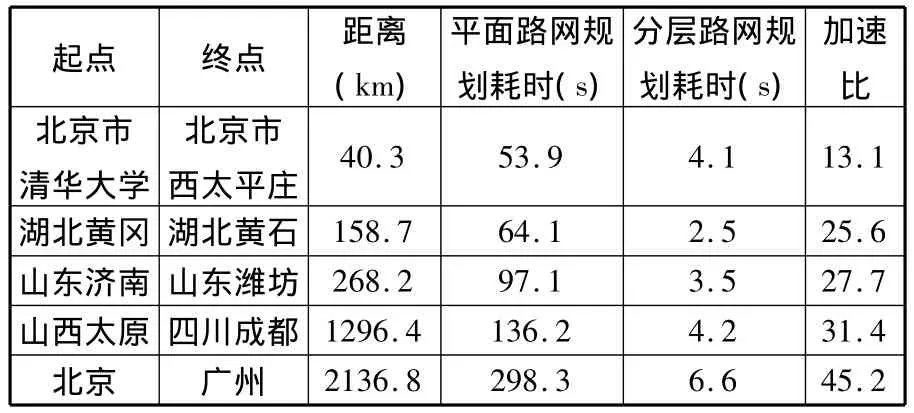
表3 分層路網路徑規劃與平面路網路徑規劃對比

由表3可以看出，分層路徑規劃算法在路網不同道路密度和分布的情況下，能夠在運算資源有限的嵌入式平臺下實現快速而準確的最優路徑計算，在廣域路網中長距離路徑規劃的計算耗時最長約為7s，能夠滿足實際應用的要求。

4 結語

本文提出了一種基于街區的路網分塊方法，該方法利用路網的分布特性，自適應調整路網分塊中數據的大小，在保持路網拓撲結構的情況下提高了路網數據的讀取效率;路網分層使規劃在高層稀疏路網中拓展，從而減少路徑規劃拓展節點的數量，在距離較遠的路徑規劃中分層路網對速度提高更明顯，分塊分層的路徑規劃算法可以應用于大規模路網中，路徑規劃的效果可以滿足用戶的需求。

［1］Zhang Tao，Yang Diange，Li Ting，et al.An Improved Virtual Intersection Model for Vehicle Navigation at Intersections［J］.Transportation Research Part C:Emerging Technologies，2011，19(3):413-423.

［2］王檀彬，陳無畏，焦俊，等.多傳感器融合的智能車輛導航研究［J］.中國機械工程，2009，20(11):1381-1385.Wang Tanbin，Chen Wuwei，Jiao Jun，et al.Study on Navigation of Intelligent Vehicles Based on Multi－sensor Fusion［J］.China Mechanical Engineering，2009，20(11):1381-1385.

［3］李旭，張為公.基于聯邦濾波的智能車輛多傳感器組合導航的研究［J］.中國機械工程，2008，19(12):1446-1451.Li Xu，Zhang Weigong.Research on Multi－sensor Integrated Navigation Technique Based on Federated Filter for Intelligent Vehicle［J］.China Mechanical Engineering，2008，19(12):1446-1451.

［4］李挺.車輛自主導航的廣域蛛式地圖與點狀路網跨層路徑規劃［D］.北京:清華大學，2008.

［5］王文璽，肖世德，孟祥印，等.模糊神經網絡下基于強化學習的自主式地面車輛路徑規劃研究［J］.中國機械工程，2009，20(21):2536-2541.Wang Wenxi，Xiao Shide，Meng Xianyin，et al.ALV Path Planning Based on Reinforcement Learning in Fuzzy Neural－networks［J］.China Mechanical Engineering，2009，20(21):2536-2541.

［6］Dijkstra E W.A Note on Two Problems in Connexion with Graphs［J］.Numerische Mathematik，1959，1:269-271.

［7］Hart P E，Nilsson N J，Raphael B.A Formal Basis for the Heuristic Determination of Minimum Cost Paths［J］.IEEE Transportation System Science and Cybernetics，1968，4(2):100-107.

［8］Hart P E，Nilsson N J，Raphael B.Correction to“A Formal Basis for the Heuristic Determination of Minimum Cost Paths”［J］.ACM SIGART Bulletin，1972，37:28-29.

［9］李清泉，鄭年波，徐敬海，等.一種基于道路網絡層次拓撲結構的分層路徑規劃算法［J］.中國圖象圖形學報，2007，12(7):1280-1285.Li Qingquan，Zheng Nianbo，Xu Jinghai et al.A Hierarchical Route Planning Algorithm Based on Multilevel Topological Structure of Road Network［J］.Journal of Image and Graphics，2007，12(7):1280-1285.

［10］顏波.車載自主導航系統中的最優路徑規劃［D］.北京:清華大學，2004.

［11］Jagadeesh G R，Srikanthan T，Quek K H .Heuristic Techniques for Accelerating Hierarchical Routing on Road Networks［J］.IEEE Transactions on Intelligent Transportation Systems，2002，3(4):301-309.

［12］Geisberger R，Sanders P，Schultes D，et al.Contraction Hierarchies:Faster and Simpler Hierarchical Routing in Road Networks［J］.Lecture Notes in Computer Science，2008，5038:319-333.

［13］Rajagopalan R，Mehrotra K，Mohan C，et al.Hierarchical Path Computation Approach for Large Graphs［J］.IEEE Transaction on Aerospace and Electronic Systems，2008，44(2):427-440.

［14］鄭煙武.基于分層分區的動態路徑規劃算法研究［D］.廣州:華南理工大學，2011.

［15］Song Qing，Wang Xiaofan.Efficient Routing on Large Road Networks Using HierarchicalCommunities［J］.IEEE Transactions on Intelligent Transportation Systems，2011，12(1):132-140.

［16］張靜.面向路徑規劃的導航路網數據模型研究［D］.北京:中國礦業大學，2009.