耦合分數階布朗馬達在非對稱勢中的輸運*

王飛 鄧翠 屠浙 馬洪?

1)(四川大學數學學院,成都 610064)

2)(電子信息控制重點實驗室,成都 610036)

(2012年7月17日收到;2012年9月20日收到修改稿)

1 引言

關于布朗馬達[1]問題的研究,最初是源于熱力學中有關第二類永動機問題的爭論,以及希望對一些復雜的輸運機制給出合理解釋.以往的研究大多集中于對單個布朗馬達輸運機制的分析[2,3],但在許多情況下粒子之間的相互作用是不可避免的,甚至有時起著決定性作用.最近二十年,在對耦合布朗馬達的研究中,發現耦合能夠促使粒子鏈有更快的平均流速[4,5],而驅動力頻率對粒子鏈的運動方向也有顯著影響[6],并且在對稱周期勢下粒子鏈也能產生定向輸運[7,8]等.隨著分子操縱技術的發展,耦合布朗馬達的定向輸運問題開始受到化學和生物學等不同學科領域的密切關注[9,10].在化學方面,應用Frenkel-Kontorova(FK)模型研究了鏈狀分子十六烷的輸運現象[11];在生物學的分子馬達研究中,發現許多稍大的分子馬達實際具有復雜的內部結構,即具有如雙頭和多頭肌動蛋白馬達這樣的多自由度特殊結構,多個這樣的分子馬達相互作用時就會產生復雜的輸運現象[12,13].但目前關于耦合布朗馬達輸運現象的研究仍大多局限于整數階動力系統[1?13].

越來越多的研究表明,粒子在黏性介質中的運動具有“記憶性”,這是整數階動力系統難以刻畫的,而近年迅速發展起來的分數階隨機微分方程理論,則特別適合于描述具有記憶、遺傳和路徑依賴性的物理、化學和生物學現象[14,15],為研究耦合布朗馬達在具有“記憶性”黏性介質中的輸運現象提供了嶄新的數學工具.

本文應用分數階FK模型研究粒子鏈在黏性介質中的定向輸運現象.通過數值模擬,觀察到整數階動力系統情況下所沒有的定向輸運反向流;此外,還討論了階數、耦合強度和噪聲強度分別對粒子鏈的平均流速的影響,發現當固定噪聲強度時,粒子鏈的平均流速隨耦合強度、階數的變化會產生廣義共振;而當階數固定時,粒子鏈的平均流速則會隨噪聲強度的變化出現廣義隨機共振現象.

2 模型建立

2.1 經典的FK模型

考慮經典的FK模型[16,17],如圖1所示,周期長為l的棘齒勢V(x),在外力yi(t)和噪聲的驅動下,忽略慣性效應,系統運動方程為

其中k為耦合強度,D為噪聲強度,設粒子間自由長度為a,不顯含于上式,γ為阻尼系數,為方便通常設 γ=1,ξi(t)為高斯白噪聲:〈ξi(t)〉=0,

圖1 FK模型原理圖

2.2 分數階FK模型

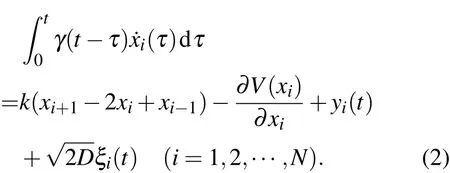
然而在很多物理和生化環境中,黏性介質對速度通常具有冪律記憶性:距當前時刻越近,記憶性越強;距當前時刻越遠,記憶性越差.描述這種退色記憶性的阻尼核函數γ(t)為[21]

為方便通常設γ0=1.

由圖2可以看出,γ(t)隨著時間t的增加按t的冪次逐漸衰減,α越大γ(t)衰減越快,α越小γ(t)衰減越慢.

把(3)式帶入(2)式得到

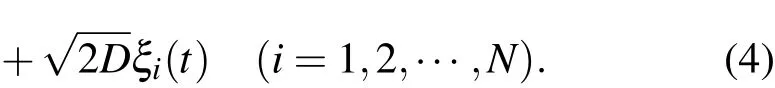
根據Caputo分數階微積分的定義[22,23],上式可以寫為

稱(5)式為分數階FK模型.

圖2 分數階阻尼核函數γ(t)

2.3 模型說明

這里所關心的重點是耦合系統粒子鏈的平均流速[5],定義如下:

其中N是系統中的粒子數,T為總時間.平均流速是一個宏觀物理量,反映了粒子運動的一個整體趨勢.

圖3 勢函數V(x)示意圖

我們選用一個周期l=1的棘輪勢,形式為

V(x)的示意圖如圖3.

對外力yi(t),要求滿足〈yi(t)〉=0,即外力無偏置.這里主要考慮yi(t)為對稱的周期力

其中A為周期力幅度,ω為周期力的角頻率.

3 數值模擬

當粒子間沒有相互作用,即k=0時,系統轉化為外力作用下的單粒子在棘輪勢中的運動;當粒子間相互作用趨于無窮大,即k→∞時,所有粒子都被剛性束縛在一起,系統的動力學行為相當于單個粒子在有效勢中的運動[5].本文排除上述極端情況,主要考慮對于有限大小的耦合強度k,粒子間的相互作用所引起的復雜定向輸運行為.

為了模擬方程(5)所刻畫的粒子運動,我們采用分數階差分法[22].采樣步長?t=0.005 s,仿真時間取50 s,粒子數N=10,角頻率ω=1,噪聲強度D=0.1,采用周期邊界.

需要指出的是,粒子xi在時刻t受到的阻尼力即t時刻的阻尼力是時段[0,t]內的速度關于阻尼核γ(t)的加權平均.當階數α→1時,即系統的記憶性變差,核函數γ(t)的衰減加快,這意味著歷史速度對當前阻尼力貢獻減少,阻尼力變弱,導致粒子具有更快的輸運速度;而當階數α降低時,即系統的記憶性增強,歷史速度對當前阻尼力貢獻增強,阻尼力也隨之增強,致使定向輸運的速度減緩,甚至當這種記憶性增強到某一程度時,促使粒子反向越過勢壘,形成定向輸運反向流.

對不同強度的周期力和不同大小的耦合強度,圖4給出了平均流速v與階數α的關系.

圖4 不同耦合強度和周期力幅度下,粒子鏈平均流速v與階數α的關系 (a)k=0;(b)k=3;(c)k=5;(d)k=10

在周期力強度較弱時(A=0,1),小周期力不足以使得單個粒子越過勢壘,粒子只能在勢阱中徘徊.當粒子間不存在相互作用,即k=0時,眾粒子的運動不能相互協調,各粒子在時刻t所受阻尼力的方向也不盡相同,即使較小的階數α導致歷史速度對當前阻尼力貢獻較強,也不足以使得單個粒子越過勢壘形成定向輸運;但若粒子間存在相互作用,即k＞0時,耦合使得粒子間的運動相互協調,各粒子在時刻t所受阻尼力也就具有較大的同向分量,加之小周期力和噪聲的作用,這樣當階數足夠小時,粒子鏈將形成定向輸運反向流.

在受到較強的周期力時,周期力能促使單個粒子越過勢壘.我們觀察到,若階數α→1時,系統的記憶性變差,有正的定向流出現;但當α→α0(α0為v(α)與橫坐標交點所對應的階數,參見圖4)時,系統的記憶性增強導致粒子運動的阻尼力增強,平均流速v將減小并趨于0;隨著階數α繼續減小,將會出現定向輸運反向流,并在負方向上出現一個共振峰值.對于不同的周期力強度,發現在A=5的時候,對應著較大的正向平均流速,說明系統在階數和耦合強度固定時,存在一個使粒子鏈平均流速極大的A.并且對于具有較大正向平均流速的A,要使系統出現定向輸運反向流的阻尼力也應較大,因此對阻尼力有實質貢獻的歷史時間需要更長,也就是對應于更小的α0;而當周期力幅度A相同時,隨著耦合強度k的增加,α0也增加.

對不同的階數α,圖5給出了周期力幅度A=2.3時,平均流速v與耦合強度k的關系.當α=1和0.8時,可以明顯觀察到正向上的共振曲線,即在某一優化耦合強度下系統存在正向極大平均流速.隨著階數下降到0.5,系統記憶性增強,系統產生了反向流,并隨k增加,在負向上出現了共振曲線,即在k≈3時,粒子鏈存在負向極大平均流速.這組曲線表明:太弱的耦合不能使得粒子之間形成統一的躍遷;太強的耦合,所有粒子束縛在一起,同樣限制了粒子鏈的輸運;適當的耦合強度可以使粒子鏈的輸運速度達到極值.

圖5 不同階數下,粒子鏈平均流速v與耦合強度k的關系 (a)α=1.0;(b)α=0.8;(c)α=0.5

圖6 階數固定情況下,輸運速度v與噪聲強度D關系

圖7 不同階數下,各粒子平均位移隨時間的演化 (a)α=0.6;(b)α=0.8

固定A=1.6,k=3,圖6展示了平均流速v與噪聲強度D的關系.我們發現當階數為1時,系統不具有記憶性,平均流速v在正向上產生了廣義隨機共振現象.當α=0.8時,系統記憶性較弱,觀察到了與整數階情況相同的現象,但在噪聲強度較弱的時候(D＜8),平均流速明顯快于整數階情況,這主要是由于在具有記憶性的系統中,歷史速度對當前阻尼力有貢獻,而歷史速度受到歷史噪聲的影響,因此歷史噪聲間接地對當前速度做出貢獻,所以較之整數階情況,達到極大平均流速所需要的噪聲強度明顯下降.而當階數減少到0.6時,系統記憶性再增強,平均流速v隨噪聲強度D的增加在負向上產生了廣義隨機共振現象.

固定噪聲強度D=5,圖7給出α分別為0.6及0.8時,各粒子平均位移〈xi(t)〉的時間演化.可以明顯地看出,當α=0.6時粒子整體向負方向運動,而α=0.8時粒子整體向正方向運動.這同樣證實了前文的結論:分數階的階數,即系統的記憶性,對粒子鏈的運動方向有顯著影響.

4 結論

本文主要研究了粒子鏈在階數和其他參數相互作用下的復雜輸運現象.得到以下結論:1)系統的記憶性即系統的階數對粒子鏈的運動狀態有顯著影響,在固定其他參數時,調節階數將導致粒子鏈出現定向輸運反向流,并在某一階數產生隨機共振;2)不同階數的噪聲-平均流速曲線v(D)表明,分數階系統出現極大平均流速所需的噪聲強度較之整數階系統更小;并且在小噪聲狀態下,平均流速明顯快于整數階系統;3)當階數固定時,耦合強度-平均流速曲線v(k)表明,平均流速會隨耦合強度的變化出現廣義共振,當階數較大即系統記憶性較弱時,出現正向粒子流的廣義共振,而當階數較小即系統記憶性較強時,則出現反向粒子流的廣義共振.

[1]H¨anggi P,Marchesoni F 2009 Rev.Mod.Phys.81 387

[2]Qian M,Wang Y,Zhang X J 2003 Chin.Phys.Lett.20 810

[3]Ai B Q,He Y F 2010 J.Chem.Phys.132 094504

[4]Wang H Y,Bao J D 2004 Physica A 337 13

[5]Csah′ok Z,Family F,Vicsek T 1997 Phys.Rev.E 55 5179

[6]Ai B Q,He Y F,Zhong WR 2011 Phys.Rev.E 83 051106

[7]Kumar K V,Ramaswamy S,Rao M 2008 Phys.Rev.E 77 020102

[8]Gehlen S V,Evstigneev M,Reimann P 2009 Phys.Rev.E 79 031114

[9]Fendrik A J,Romanelli L 2012 Phys.Rev.E 85 041149

[10]Zheng Z G 2004 Spatiotemporal Dynamics and Collective Behaviors in Coupled Nonlinear Systems(Beijing:Higher Education Press)p279(in Chinese)[鄭志剛2004耦合非線性系統的時空動力學與合作行為(北京:高等教育出版社)第279頁]

[11]Vadakkepatt A,Dong Y L,Lichter S,Martini A 2011 Phys.Rev.E 84 066311

[12]Nishikawa M,Takagi H,Shibata T,Iwane A H,Yanagida T 2008 Phys.Rev.Lett.101 128103

[13]Camp`as O,Kafri Y,Zeldovich K B,Casademunt J,Joanny J F 2006 Phys.Rev.Lett.97 038101

[14]Liu F,Anh V V,Turner I,Zhuang P 2003 J.Appl.Math.Comp.13 233

[15]de Andrade M F,Lenzi E K,Evangelista L R,Mendes R S,Malacarne L C 2005 Phys.Lett.A 347 160

[16]Braun O M,Kivshar Y S 2004 The Frenkel-Kontorova Model:Concepts,Methods and Application(New York:Springer)

[17]Han X Q,Jiang H,Shi Y R,Liu Y X,Sun J H,Chen J M,Duan W S 2011 Acta Phys.Sin.60 116801(in Chinese)[韓秀琴,姜虹,石玉仁,劉妍秀,孫建華,陳建敏,段文山2011物理學報60 116801]

[18]Bao J D 2009 Random Simulation Method of Classical and Quantum Dissipation System(Beijing:Science Press)p80(in Chinese)[包景東2009經典和量子耗散系統的隨機模擬方法(北京:科學出版社)第80頁]

[19]Oldham K B,Spanier J 1974 The Fractional Calculus(New York:Academic Press)

[20]Kou S C,Xie X S 2004 Phys.Rev.Lett.93 180603

[21]Gao S L,Zhong S C,Wei K,Ma H 2012 Acta Phys.Sin.61 100502(in Chinese)[高仕龍,鐘蘇川,韋鹍,馬洪2012物理學報61 100502]

[22]Podlubny I 1999 Fractional Differential Equations(San Diegop,CA:Academic Press)

[23]Samko S G,Kilbas A A,Marichev O I 1993 Fractional Integrals and Derivatives Theory and Applications(New York:Gordon and Breach Science Publisher)