一種數(shù)字控制三相逆變電路的局部振蕩行為分析*

雷博 肖國春 吳旋律

(西安交通大學(xué)電氣工程學(xué)院,電力設(shè)備電氣絕緣國家重點實驗室,西安 710049)

(2012年7月10日收到;2012年9月18日收到修改稿)

1 引言

隨著全球化能源危機的不斷加劇,利用風(fēng)能、光伏發(fā)電等可再生能源的分布式發(fā)電系統(tǒng)得到了廣泛的關(guān)注.在這些分布式發(fā)電系統(tǒng)中,逆變電路作為可再生能源與電網(wǎng)之間的“連接橋梁”起到了重要的作用[1],得到了廣泛的應(yīng)用.數(shù)字控制技術(shù)的發(fā)展,使得目前在實際工程應(yīng)用中三相逆變電路一般工作在數(shù)字控制脈寬調(diào)制(PWM)模式下[2].同時,由于數(shù)字控制中一拍延時的引入,對系統(tǒng)的穩(wěn)定性以及動態(tài)特性會產(chǎn)生較大的影響[3,4].對數(shù)字控制三相逆變電路的動力學(xué)特性進行準(zhǔn)確的建模分析是非常必要的.

已有許多學(xué)者對單相全橋無源逆變電路的動力學(xué)特性進行了分析[5?13],同時觀測到豐富的非線性現(xiàn)象,如邊界碰撞分岔[5?7,11]、倍周期分岔[8?10]以及Hopf分岔[8,10,12,13].文獻[5—7]建立了一階數(shù)字控制單相全橋電路工作在DC-DC狀態(tài)下的離散迭代映射,并提出了可以提高系統(tǒng)穩(wěn)定性的改進延時反饋策略.文獻[9]通過分析一階數(shù)字控制單相全橋逆變電路的非線性行為,提出了慢變穩(wěn)定性定理.文獻[11]分析了一階數(shù)字控制單相全橋逆變電路在對稱PWM調(diào)制下的邊界碰撞分岔現(xiàn)象.但文獻[5—7,9]目前并沒有對與數(shù)字控制系統(tǒng)穩(wěn)定性密切相關(guān)的一拍延時的影響進行分析.同時,文獻[5—11]在推導(dǎo)系統(tǒng)的離散迭代模型時,直接利用狀態(tài)轉(zhuǎn)移矩陣進行分析.當(dāng)系統(tǒng)階數(shù)高于2階時,由于狀態(tài)轉(zhuǎn)移矩陣的元素與狀態(tài)變量有關(guān)并且無法解析表達,無法解析描述系統(tǒng)每個狀態(tài)變量與系統(tǒng)參數(shù)的關(guān)系.這時,通常需要借助計算機數(shù)值計算循環(huán)描點才能表示出系統(tǒng)參數(shù)與系統(tǒng)運動行為的關(guān)系[8?10].文獻[12,13]在考慮了數(shù)字控制系統(tǒng)延時的情況下,通過解析表達狀態(tài)轉(zhuǎn)移矩陣中各個元素,對單相全橋無源逆變器建立了數(shù)學(xué)模型,分析了LC型濾波器以及LC L型濾波器單相無源逆變電路系統(tǒng)中復(fù)雜行為的內(nèi)在機理,得到了其參數(shù)的穩(wěn)定范圍的解析表達式并準(zhǔn)確預(yù)測了系統(tǒng)發(fā)生不穩(wěn)定現(xiàn)象.這些工作加深了對單相全橋逆變電路的理解,但均集中在單相系統(tǒng)中.同時,上述工作中的慢尺度不穩(wěn)定現(xiàn)象在一個工頻周期內(nèi)是同時發(fā)生的.而在三相逆變系統(tǒng)中,系統(tǒng)可能會產(chǎn)生局部的振蕩現(xiàn)象.在考慮一拍數(shù)字延時以及解析表達狀態(tài)轉(zhuǎn)移矩陣中元素的前提下,對數(shù)字控制三相逆變電路利用離散迭代模型分析其局部振蕩行為的工作迄今為止未見報道.

本文針對一種數(shù)字控制三相逆變電路,通過解析表達狀態(tài)轉(zhuǎn)移矩陣中元素、考慮數(shù)字控制中的一拍計算、控制延時并考慮到三相電路中的不平衡因素,建立了系統(tǒng)的離散迭代模型.利用本文提出的離散迭代模型,系統(tǒng)參數(shù)與系統(tǒng)運動行為之間的關(guān)系可以得到直觀的解析描述.進一步,本文提出了系統(tǒng)發(fā)生Hopf分岔、倍周期分岔以及鞍階分岔的解析判別式.利用本文提出的離散迭代模型及不穩(wěn)定行為判別式,準(zhǔn)確預(yù)測了本文研究系統(tǒng)的不穩(wěn)定現(xiàn)象及穩(wěn)定邊界.同時,對系統(tǒng)產(chǎn)生的局部振蕩現(xiàn)象進行了分析,得出了這種現(xiàn)象產(chǎn)生的物理機理及產(chǎn)生條件.最后,通過Simulink仿真以及電路實驗驗證了理論分析的正確性.

利用離散迭代模型,本文建立了數(shù)字控制三相逆變電路中系統(tǒng)參數(shù)以及系統(tǒng)運動行為之間解析聯(lián)系,揭示了三相逆變系統(tǒng)的耦合關(guān)系,發(fā)現(xiàn)了局部振蕩現(xiàn)象,指出了局部振蕩的產(chǎn)生條件,準(zhǔn)確預(yù)測了系統(tǒng)參數(shù)和局部振蕩起始點之間的關(guān)系,同時簡化了利用離散迭代模型對系統(tǒng)不穩(wěn)定行為預(yù)測的過程,有利于實際工程應(yīng)用.

2 電路工作原理及離散迭代模型建立

數(shù)字控制三相逆變電路的主要功能是對逆變電流的穩(wěn)定控制,保證逆變電流符合設(shè)計要求.逆變電路以固定的開關(guān)頻率 fs運行,逆變電流頻率為f,角頻率為ω.電路由主電路部分以及數(shù)字控制部分組成,系統(tǒng)結(jié)構(gòu)如圖1所示.主電路部分由直流側(cè)電壓源E、三相逆變逆變器和三相阻感負載Ra,Rb,Rc及La,Lb,Lc構(gòu)成.數(shù)字控制部分由采樣環(huán)節(jié)、三相靜止坐標(biāo)系到兩相同步坐標(biāo)系的正變換及反變換環(huán)節(jié)、數(shù)字控制器、歸一化環(huán)節(jié)、限幅器及數(shù)字PWM發(fā)生器組成.系統(tǒng)采取了兩相旋轉(zhuǎn)坐標(biāo)系下的逆變電流反饋環(huán)的控制方式,其中電流環(huán)采取的是比例(P)控制器.圖1中,CM環(huán)節(jié)代表電流采樣環(huán)節(jié);θs是給定逆變相位;idref和iqref是兩相旋轉(zhuǎn)坐標(biāo)系下的給定值,是一個直流信號;ia,ib,ic分別為三相逆變電流;ia,ib,ic結(jié)合θs通過三相靜止坐標(biāo)系到兩相旋轉(zhuǎn)坐標(biāo)系變換公式(DQ變換)得到兩相同步旋轉(zhuǎn)坐標(biāo)系下的逆變電流id,iq;kpd,kpq分別為d軸與q軸下的比例系數(shù);d軸以及q軸的輸出信號分別為vdx以及vqx;vdx,vqx結(jié)合θs通過兩相旋轉(zhuǎn)坐標(biāo)系到三相靜止坐標(biāo)系變換公式(DQ反變換),進行歸一化及限幅環(huán)節(jié)得到三相的控制信號vax,vbx,vcx;其中ksat為歸一化系數(shù),其大小為1/(2E).在每個開關(guān)周期的起始階段,系統(tǒng)通過采樣、計算各個電氣量,利用數(shù)字PWM發(fā)生器產(chǎn)生占空比信號以驅(qū)動S1—S6運行.

圖1 數(shù)字控制三相逆變電路系統(tǒng)

本文采用的數(shù)字控制雙極性正弦脈沖調(diào)制(SPWM)策略如圖2所示.上下兩個橋臂工作在互補狀態(tài),即若上管導(dǎo)通則下管關(guān)閉,反之亦然.各個橋臂的開關(guān)狀態(tài)分別由控制信號vax,vbx,vcx與三角載波的大小關(guān)系決定.由于數(shù)字控制中的采樣計算延時[3,4],第n個開關(guān)周期的占空比狀態(tài)dan,dbn和dcn由第(n?1)個開關(guān)周期的控制信號vax(n?1),vbx(n?1),vcx(n?1)決定,占空比信號的值為0或者1.當(dāng)dna=1時代表S1開通S4關(guān)閉,dna=0時代表S1關(guān)閉S4開通;當(dāng)dnb=1時代表S3開通S6關(guān)閉,dna=0時代表S3關(guān)閉S6開通;當(dāng)dnc=1時代表S5開通S2關(guān)閉,dnc=0時代表S5關(guān)閉S2開通.

圖2 數(shù)字SPWM調(diào)制策略示意圖

2.1 控制電路離散迭代模型描述

根據(jù)兩相旋轉(zhuǎn)坐標(biāo)系到三相靜止坐標(biāo)系變換關(guān)系,vax,vbx,vcx三相控制信號之和為0,所以三個占空比信號也只有兩個自由度.本文中選取a相及b相占空比作為狀態(tài)變量.由于逆變電流是正弦信號,系統(tǒng)是一個周期時變系統(tǒng).但由于 fs遠大于 f,同時系統(tǒng)采用數(shù)字控制,在一個開關(guān)周期內(nèi)只進行一次電氣量的采樣、計算及占空比信號的載入,通過準(zhǔn)靜態(tài)分析[14],可以認為在一個開關(guān)周期內(nèi)三相逆變電流是恒值.由于數(shù)字系統(tǒng)中的采樣保持過程,根據(jù)系統(tǒng)的控制原理可以直接得出系統(tǒng)控制部分的離散迭代方程.

設(shè)iden,iqen和vdxn,vqxn分別是第n個開關(guān)周期d軸和q軸下誤差信號以及控制器輸出信號;kdp,kqp分別是d軸和q軸下的比例控制參數(shù);設(shè)ian,ibn,icn,θsn分別代表第nTs時刻三相逆變電流和旋轉(zhuǎn)坐標(biāo)同步角的采樣值.得出da和db的離散迭代方程為

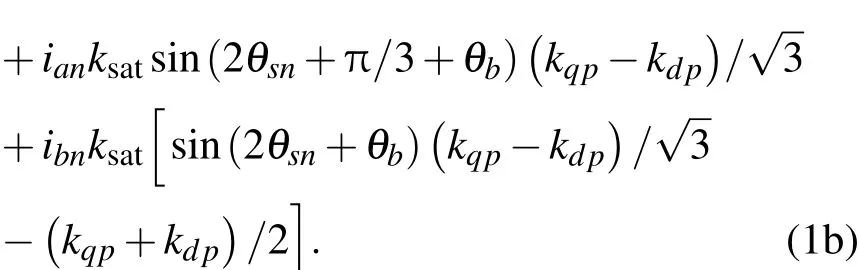
根據(jù)三相關(guān)系,得到dcn與dan,dbn的關(guān)系為

通過(1)式可以得到系統(tǒng)占空比的迭代方程,具體推導(dǎo)過程見附錄1.

2.2 主電路離散迭代模型描述

根據(jù)基爾霍夫電流定律,三相電流之和為0,三相電流只有兩個自由度.選取其中兩相逆變電流i=[iaib]T作為狀態(tài)變量.設(shè)AT,BET,(T=000,111,100,110,101,010,011,001)是系統(tǒng)在不同拓撲下的狀態(tài)矩陣.從圖3中可以看出,當(dāng)系統(tǒng)的開關(guān)狀態(tài)發(fā)生變化時,只有直流側(cè)電壓的狀態(tài)發(fā)生改變,令A(yù)T=A.A和BET的具體表達式見附錄2.同時,為了方便描述,定義θa=0,θb=?2π/3和θb=2π/3.

系統(tǒng)主電路部分在各個拓撲狀態(tài)下的狀態(tài)方程為

在系統(tǒng)第n個開關(guān)周期的運行過程中,根據(jù)dan,dbn和dcn的大小關(guān)系,結(jié)合圖2和圖3,系統(tǒng)將會演化出6種不同的拓撲序列結(jié)構(gòu),如圖4所示.

由于系統(tǒng)采用的是對稱SPWM調(diào)制策略,系統(tǒng)可能的拓撲序列為T000→Tα→Tβ→T111→Tβ→Tα→T000.其中[α,β]有[100,110],[100,101],[010,110],[010,011],[001,101]和[001,011]6種可能性.

結(jié)合(2)式,對拓撲序列進行分段積分.積分結(jié)果表明,系統(tǒng)在這六種可能拓撲序列中的離散迭代方程是相同的,可以表示為

其中

系統(tǒng)離散迭代模型的推導(dǎo)過程及BEa,BEb和BEc的具體表達形式見附錄3.

圖3 三相逆變器拓撲狀態(tài)示意圖 (a)T000;(b)T100;(c)T010;(d)T001;(e)T111;(f)T011(g)T101;(h)T110

根據(jù)(1)和(3)式可以得出系統(tǒng)的離散迭代方程,其中數(shù)字控制部分由于一拍延時作用,得到的是各相獨立的“標(biāo)量化”離散迭代方程,但是主電路迭代模型(3)式直接使用狀態(tài)轉(zhuǎn)移矩陣進行分析,無法得出各相逆變電流之間、逆變電流與系統(tǒng)參數(shù)、逆變電流與各相占空比之間的解析關(guān)系.利用矩陣A的特征值和特征向量,可以描述狀態(tài)轉(zhuǎn)移矩陣[15],同時利用文獻[12,13]中提出的方法,對此離散迭代方程進行標(biāo)量化描述.

設(shè)λA1,λA2為矩陣A的特征值,數(shù)字控制三相逆變器主電路中a,b兩相的標(biāo)量化離散迭代方程為

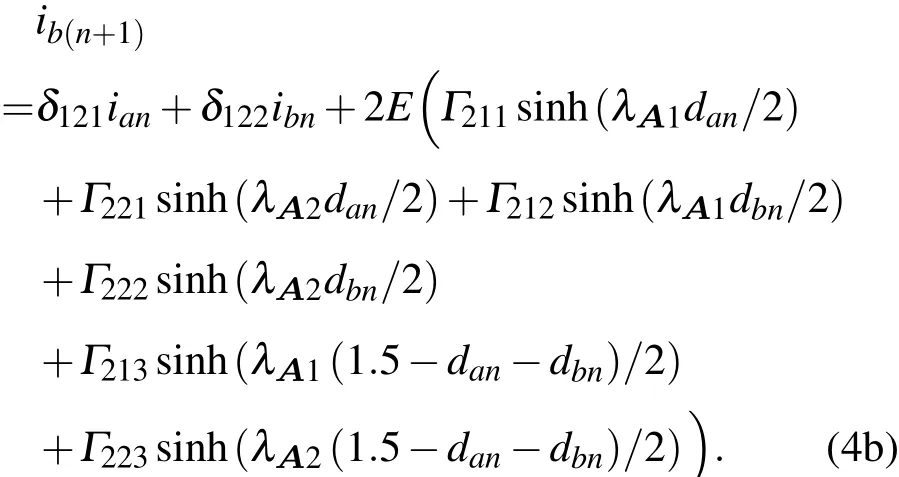
同時,根據(jù)三相之間的關(guān)系,得到c相的表達式為

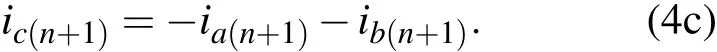
(4)式的推導(dǎo)過程以及函數(shù) δ,Γχ1χ2χ3(χ1,χ2,χ3=1,2,3)及 φvsy1y2(y1,y2=a,b)的定義詳見附錄4.

圖4 第n個開關(guān)周期系統(tǒng)可能的拓撲情況 (a)dan＞dbn＞dcn;(b)dbn＞dan＞dcn;(c)dcn＞dan＞dbn;(d)dan＞dcn＞dbn;(e)dbn＞dcn＞dan;(c)dcn＞dbn＞dan

結(jié)合(1a),(1b),(4a)和(4b)式,可以得出在兩相同步旋轉(zhuǎn)坐標(biāo)系下采用P控制、各相為阻感負載時的數(shù)字控制三相逆變電路的標(biāo)量化離散迭代模型.系統(tǒng)共含有4個獨立的狀態(tài)變量,ia,ib,da,db.在下一節(jié)將通過分析系統(tǒng)在平衡點處的雅克比矩陣特征值來對系統(tǒng)的運動行為以及穩(wěn)定特性進行分析.

3 系統(tǒng)穩(wěn)定性分析

3.1 系統(tǒng)的穩(wěn)定特性

通過準(zhǔn)靜態(tài)分析[14],結(jié)合(1)和(4)式,令dbn可以求出系統(tǒng)的平衡點.根據(jù)系統(tǒng)開關(guān)頻率和工頻頻率之間的關(guān)系,系統(tǒng)共有 fs/f個平衡點.需要注意的是,求解平衡點的方程是超越方程,需要利用牛頓下山法等數(shù)值算法進行求解.系統(tǒng)的平衡點分別設(shè)為,,和(0＜l≤fs/f),設(shè)l為系統(tǒng)平衡點序列的序號.

系統(tǒng)在第l個平衡點的雅克比矩陣可以寫為

根據(jù)(5)式,得出了系統(tǒng)在第l個平衡點的特征方程為

其中,F0—F3具有解析的表達式,其具體參數(shù)表達式詳見附錄5.同時,根據(jù)根與系數(shù)的關(guān)系,設(shè)λJ1—λJ4為(6)式的根,系統(tǒng)的特征方程同樣可以描述為

隨著系統(tǒng)控制參數(shù)的增大變化,系統(tǒng)的特征根會穿出單位圓,系統(tǒng)會發(fā)生不穩(wěn)定行為.當(dāng)系統(tǒng)中有一對共軛虛根穿出單位圓,而余下的特征根在單位圓內(nèi),系統(tǒng)會發(fā)生Hopf分岔[14];當(dāng)有一個特征值等于1,而其他特征值在單位圓內(nèi),系統(tǒng)會發(fā)生鞍結(jié)分岔;當(dāng)一個特征根等于?1,而其他特征值在單位圓內(nèi),系統(tǒng)會發(fā)生倍周期分岔[16?19].

根據(jù)系統(tǒng)控制規(guī)律,kdp和kqp均大于0.在表1所示的系統(tǒng)參數(shù)下,在系統(tǒng)的每個平衡點處,以系統(tǒng)控制kdp和kqp為變量,可以對(8)式所代表的三個邊界曲線bH,bS和bP在第一象限繪制出一組曲線.通過三條曲線之間的關(guān)系,可以預(yù)測出系統(tǒng)將會發(fā)生的不穩(wěn)定現(xiàn)象,以及各種不穩(wěn)定現(xiàn)象發(fā)生時的邊界控制參數(shù).

根據(jù)表1中參數(shù)定義,依據(jù)準(zhǔn)靜態(tài)分析,在一個工頻周期內(nèi),系統(tǒng)共含有300個平衡點.在系統(tǒng)的300個平衡點上,根據(jù)(8)式代表的三種分岔行為判別式,分別繪制三種邊界曲線.根據(jù)三種邊界曲線之間的穩(wěn)定性關(guān)系,可以發(fā)現(xiàn),在這個數(shù)字控制三相逆變器系統(tǒng)中,系統(tǒng)只會發(fā)生Hopf分岔,而不會發(fā)生其他的分岔類型.

表1 系統(tǒng)參數(shù)表

3.2 局部振蕩行為分析

對比(9)式中各個等式,當(dāng)kqp與kdp相等時,等于0,同時也是與系統(tǒng)平衡點序號l的無關(guān)量.但是,當(dāng)kqp與kdp不相等時,會隨著系統(tǒng)平衡點序列號l(0＜l≤fs/f)而做周期性的變化,顯然,其變化周期為工頻周期的兩倍.由此,預(yù)測系統(tǒng)在kdp不等于kqp的情況下,在一個工頻周期內(nèi),系統(tǒng)的穩(wěn)定性不一致,會出現(xiàn)局部不穩(wěn)定現(xiàn)象.根據(jù)之前分析,由于此系統(tǒng)在表1所示參數(shù)下,只會發(fā)生Hopf分岔,所以此時系統(tǒng)將會出現(xiàn)局部振蕩現(xiàn)象;而當(dāng)kdp=kqp的情況下,系統(tǒng)在一個工頻周期內(nèi)的穩(wěn)定性一致,系統(tǒng)不穩(wěn)定時,將會產(chǎn)生的是全局振蕩現(xiàn)象.下面就kdp與kqp的不同關(guān)系對系統(tǒng)的穩(wěn)定性進行分析.

根據(jù)控制器參數(shù)定義,kdp和kqp均大于0.根據(jù)3.1分析結(jié)果,在表1所示參數(shù)下,系統(tǒng)在300個平衡點上均只會發(fā)生Hopf分岔.同時考慮計算方法原理[20],為了避免數(shù)值計算誤差,以ksatkdp為橫坐標(biāo),以ksatkqp為縱坐標(biāo),從第15個平衡點開始每隔15個平衡點,畫出此時系統(tǒng)第一象限中的bH曲線組,如圖5所示.

如圖5所示,由于系統(tǒng)的特征方程(6),及相應(yīng)的Hopf分岔邊界條件(8a)中與平衡點序列號l相關(guān),所以不同的平衡點的穩(wěn)定范圍有所不同.同時系統(tǒng)的穩(wěn)定特性具有對稱性,對稱周期為工頻周期的一半.對于某一特定的控制參數(shù),在系統(tǒng)一部分平衡點處系統(tǒng)穩(wěn)定,而在其他平衡點處系統(tǒng)不穩(wěn)定,系統(tǒng)就會產(chǎn)生局部振蕩現(xiàn)象.

根據(jù)圖5所示,當(dāng)控制參數(shù)ksatkdp=0.5(kdp=100),ksatkqp=0.95(kqp=190)時,將會在第45—90平衡點處及195—240平衡點附近出現(xiàn)振蕩現(xiàn)象,而在工頻周期的其他部分,系統(tǒng)是穩(wěn)定的.

根據(jù) (9)式中各式定義,當(dāng) kdp=kqp時,和平衡點序列號 l無關(guān),則系統(tǒng)的特征方程(6)及系統(tǒng)穩(wěn)定邊界條件(8)中各式與系統(tǒng)平衡點無關(guān).此時,若系統(tǒng)發(fā)生不穩(wěn)定現(xiàn)象,那么這種不穩(wěn)定運動將在一個工頻周期內(nèi)的所有平衡點同時發(fā)生.定義此時求取穩(wěn)定邊界的方程為

此時,系統(tǒng)只有一個控制參數(shù)ksatkdp,同樣從第15個平衡點開始,以15為步進,給出(10)式的根的分布情況如圖6所示.從圖6上可以看出,不同平衡點對應(yīng)(10)式的根相同,與之前推論符合.

根據(jù)參數(shù)定義,(10)式在正半軸最小的實根即為使系統(tǒng)穩(wěn)定的最大控制參數(shù)取值.通過精確的計算,此系統(tǒng)在kdp=kqp的條件下的穩(wěn)定邊界為

對比圖5,圖中所有的穩(wěn)定邊界交匯于一點,這點坐標(biāo)下的控制參數(shù)是0.7390395(kdp=dqp=147.8079),滿足于(11)式關(guān)于kdp=kqp情況下穩(wěn)定邊界的判斷.當(dāng)系統(tǒng)控制參數(shù)不滿足(11)式時,系統(tǒng)將會在整個工頻周期內(nèi)同時發(fā)生不穩(wěn)定振蕩現(xiàn)象.

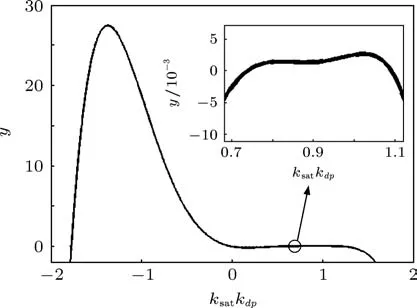
圖6 kd p=kq p時,穩(wěn)定邊界方程根的分布情況

4 仿真和實驗

根據(jù)圖1,給出系統(tǒng)相應(yīng)的Simulink仿真電路圖如圖7所示.整個仿真系統(tǒng)采用連續(xù)仿真,同時利用比較模塊以及延時模塊模擬了數(shù)字控制系統(tǒng)的采樣保持、計算延時過程.

假設(shè)3認為，對于成長期企業(yè)，碳信息披露會顯著緩解企業(yè)的融資約束。為了檢驗假設(shè)3，對處于成長期的288個樣本數(shù)據(jù)進行多元回歸。表5的假設(shè)3部分列示了碳信息披露對成長期企業(yè)融資約束影響的估計結(jié)果。結(jié)果顯示：（1）CFAt-1的系數(shù)在1%的水平下顯著為正 （系數(shù)為0.0013，t值為2.79），表明成長期的重污染企業(yè)普遍面臨較強的融資約束；（2） CFAt-1×CDI的系數(shù)在1%的水平下顯著為負 （系數(shù)為-0.2435，t值為-2.91），表明碳信息披露對成長期企業(yè)融資約束的緩解效應(yīng)顯著。假設(shè)3檢驗通過。

代入控制參數(shù)kdp=100,kqp=190,仿真結(jié)果如圖8所示.圖8中出現(xiàn)了局部振蕩現(xiàn)象,局部振蕩周期為工頻周期一半,振蕩起始、終止點與理論分析一致,證明了理論分析的有效性及精確性.

代入控制參數(shù)kdp=kqp=150,系統(tǒng)的仿真結(jié)果如圖9所示.圖9中出現(xiàn)了全局振蕩現(xiàn)象,證明了理論分析的有效性及精確性.

圖7 數(shù)字控制三相逆變系統(tǒng)仿真電路圖

圖8 kd p=100,kq p=190時系統(tǒng)仿真結(jié)果

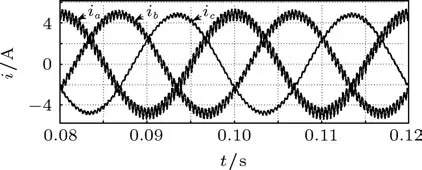
圖9 kd p=kq p=150時系統(tǒng)仿真結(jié)果

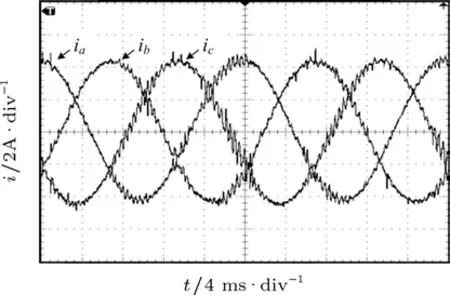
圖10 kd p=100,kq p=190時試驗波形

圖11 kd p=kq p=150時試驗波形

對三相系統(tǒng)的運動行為進行試驗研究,以驗證理論分析的正確性.實驗電路拓撲結(jié)構(gòu)與圖3相同,系統(tǒng)參數(shù)選取如表1所示.分別選取控制參數(shù)kdp=100,kqp=190;kdp=kqp=150,進行試驗,實驗結(jié)果如圖10及圖11所示.實驗結(jié)果與Simulink仿真結(jié)果相似.由于沒有考慮逆變器死區(qū)作用以及開關(guān)管的損耗等,實驗產(chǎn)生了一定的誤差.

5 結(jié)論

本文針對數(shù)字控制三相逆變電路系統(tǒng),對其在同步旋轉(zhuǎn)坐標(biāo)系比例控制下的一種局部振蕩行為進行了分析.通過解析表達狀態(tài)轉(zhuǎn)移矩陣中元素,建立了系統(tǒng)各個狀態(tài)變量離散迭代方程,從而得到了三相逆變電流之間和逆變電流與各相占空比、系統(tǒng)參數(shù)之間的內(nèi)在物理聯(lián)系.進一步,本文針對高階系統(tǒng),提出了一種運動行為解析判別式,揭示了三相逆變系統(tǒng)的耦合關(guān)系以及運動行為的內(nèi)在物理機理,準(zhǔn)確預(yù)測了系統(tǒng)的穩(wěn)定范圍以及不穩(wěn)定現(xiàn)象.

以往針對全橋逆變器,利用非線性理論進行建模分析的工作主要集中在單相領(lǐng)域,同時它們的不穩(wěn)定現(xiàn)象在一個工頻周期內(nèi)是同時發(fā)生的.通過本文對三相系統(tǒng)的研究,發(fā)現(xiàn)系統(tǒng)會發(fā)生有別于單相系統(tǒng)的局部的振蕩現(xiàn)象.本文針對這種局部振蕩現(xiàn)象,進行了理論分析,得出當(dāng)D軸比例系數(shù)與Q軸比例系數(shù)超出一定范圍且兩者不相等時,就會發(fā)生這種局部振蕩現(xiàn)象.本文得到了控制參數(shù)與局部振蕩點關(guān)系的解析表達式,并準(zhǔn)確預(yù)測了產(chǎn)生局部振蕩的起始、結(jié)束點.最后,通過Simulink仿真以及電路實驗證明了理論分析的正確性及有效性.

附錄A1

根據(jù)三相靜止坐標(biāo)系到兩相旋轉(zhuǎn)坐標(biāo)系轉(zhuǎn)化公式:

通過由此得到系統(tǒng)的誤差信號,設(shè)為iden和iqen,可以表達為

根據(jù)兩相旋轉(zhuǎn)坐標(biāo)系到三相靜止坐標(biāo)系變換公式及圖1所示控制框圖,得到vyxn(y=a,b,c)三相控制信號為

由于三相控制信號由DQ反變換得來,則三相控制信號之和為0.

結(jié)合圖3,可以得到dyn(y=a,b,c)的表達式為

結(jié)合(A7)和(A8)式,可以分別得出三相系統(tǒng)控制部分的離散迭代方程表達式.

附錄A2

A和BET在8種拓撲狀態(tài)下的表達式為

其中α1,α2和α3可以表達為

其中:

附錄A3

對(2)式進行積分,設(shè)積分起始時間為ton,結(jié)束時間為toff,拓撲結(jié)構(gòu)為Tt,積分結(jié)果為

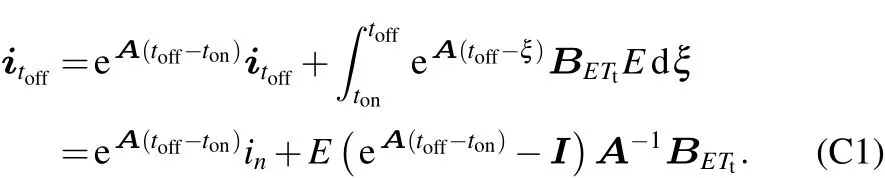
如圖7所示,系統(tǒng)可能的拓撲序列為T000→Tα→Tβ→T111→ Tβ→ Tα→T000.其中 [α,β]有 [100,110],[100,101],[010,110],[010,011],[001,101]和[001,011]六種可能性.在第n個開關(guān)周期內(nèi),設(shè)占空比最大相為g相,最小相為s相,另一相為m相,通過代入相應(yīng)參數(shù)對(C1)進行迭加,得到:

其中φEg,φEm和φEs為

可以分六種情況討論(C3)和(C4)的表達式變化,在此以[α,β]=[100,110]時為例進行分析.此時占空比最大的為a相,最小的為c相,則

對于其他5種情況,均可以寫出相應(yīng)的BEa,BEa和BEa表達式.根據(jù)附錄1中定義,發(fā)現(xiàn)在六種情況下BEa,BEa和BEa的表達式相同,于是重新定義BEa,BEb和BEc:

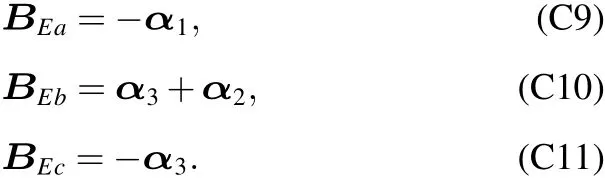
附錄A4

根據(jù)文獻[12,13]中的方法,同樣定義κ,ρ為系統(tǒng)矩陣A的特征向量矩陣及其逆矩陣,并可描述為

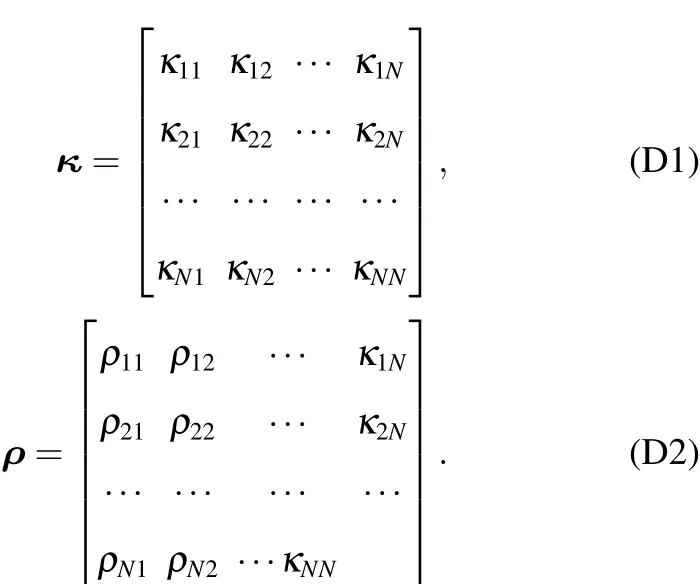
定義λAχ1,λAχ2為矩陣A的特征值.

定義函數(shù)ε(χ1,χ2,χ3):

其中χ1,χ2和χ3定位了矩陣κ,ρ元素的位置.

設(shè) ξ 為任意常數(shù),定義 δξχ2χ3:

其中r定位了向量δr(N,ξ)的位置.

則 eξA可以表述為

定義 ?1,?2和 ?3

定義函數(shù)Γrlq:

附錄A5

根據(jù)參數(shù)定義,同時考慮系統(tǒng)的開關(guān)頻率相對工頻頻率較高,設(shè)可以得出在第 l個平衡點的表達式為

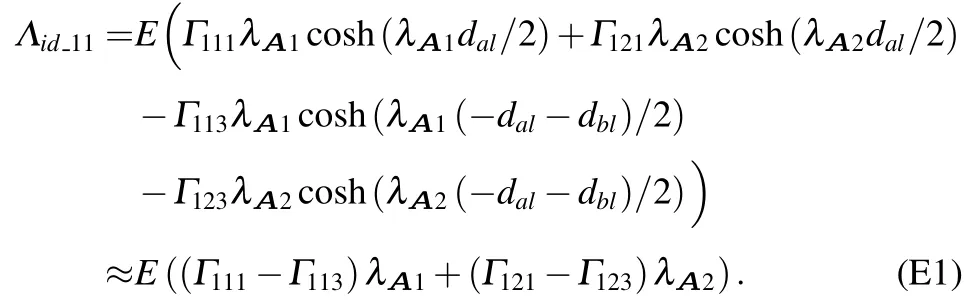
同樣可以得出:

將(1)式對ia,ib分別求偏導(dǎo),可以得出1,2)在第l個平衡點的表達式為

根據(jù)系統(tǒng)在第l個平衡點的雅克比矩陣(5),可以得出F3—F0的表達式為

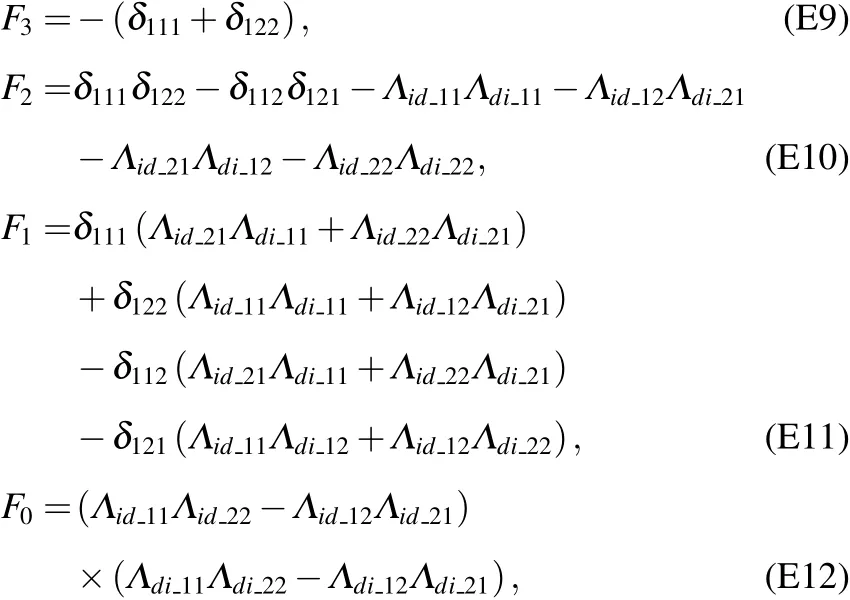
[1]Barbosa P G,Braga H A C,Rodrigues M C B,Teixeira E C 2006 IEEE Trans.Power Electron.21 1116

[2]Twining E,Holmes D G 2003 IEEE Trans.Power Electron.18 888

[3]Hyosung K,Seung K S 2005 IEEE Trans.Power Electron.20 1169

[4]Escobar G,Valdez A A 2003 IEEE Trans.Ind.Electron.54 504

[5]Robert B,Robert C 2002 Int.J.Contr.75 1356

[6]Iu H H C,Robert B 2003 IEEE Trans.Circ.Syst.I 50 1125

[7]Robert B,Iu H H C,Feki M 2004 Int.J.Circ.Syst.Comp.I 50 1125

[8]Li M,Dai D,Ma X K 2008 Circuits Syst.Signal Processing 27 811

[9]Wang X M,Zhang B,Qiu D Y 2009 Acta Phys.Sin.58 2248(in Chinese)[王學(xué)梅,張波,丘東元2009物理學(xué)報58 2248]

[10]Aroudi A E,Rodriguez E,Orabi M,Alarcon E 2010 Int.J.Circ.Theor.Appl.10 627

[11]Hiroyuki A,Takuji K 2010 Int.J.Circ.Theor.Appl.21 985

[12]Lei B,Xiao G C,Wu X L,Qi Y R 2011 Acta Phys.Sin.60 090501(in Chinese)[雷博,肖國春,吳旋律,齊元瑞2011物理學(xué)報60 090501]

[13]Lei B,Xiao GC,Wu X L 2012 Acta Phys.Sin.61 090501(in Chinese)[雷博,肖國春,吳旋律2012物理學(xué)報61 090501]

[14]Tse C 2003 Complex Behavior in Switching Power Converters(Boca Raton,CRC)p59

[15]Moler C,Loans C V 1978 Siam.Rev.20 801

[16]Wang F Q,Zhang H,Ma X K 2010 IEEE Trans.Circ.Syst.I 57 405

[17]Wang F Q,Zhang H,Ma X K 2008 Acta Phys.Sin.57 1522(in Chinese)[王發(fā)強,張浩,馬西奎2008物理學(xué)報57 1522]

[18]Zhang X T,Ma X K,Zhang H 2008 Acta Phys.Sin.57 6174(in Chinese)[張笑天,馬西奎,張浩2008物理學(xué)報57 6174]

[19]Zhang Y,Zhang H,Ma X K 2010 Acta Phys.Sin.59 8432(in Chinese)[張源,張浩,馬西奎2010物理學(xué)報59 8432]

[20]Viecelli J A 1971 J.Comput.Phys.8 119