強流電子束阻抗對相對論速調管放大器注入及群聚特性的影響分析

張澤海 舒挺 張軍 戚祖敏

(國防科技大學光電科學與工程學院,高功率微波技術研究所,長沙 410073)

(2012年8月23日收到;2012年9月17日收到修改稿)

1 引言

在速調管放大器[1]中,空間電荷效應對工作特性的影響很大,而且束流越強,影響程度越大.在強流相對論速調管放大器(relativistic klystron amplifier,RKA)中,電子束的電流達到數千安[2?4],而群聚后的局部瞬時電流則可能接近或超過漂移管中的空間電荷限制流,因此具有更強的空間電荷效應[5,6].這種空間電荷效應不僅影響RKA的調制、群聚機制[7],而且影響電子束對輸入腔的加載特性.由于RKA器件的整體長度以及輸入腔的耦合特性是由強流電子束的群聚機制及其對輸入腔的加載決定的[8],因此有必要對強流電子束阻抗、電壓及電流對RKA工作特性的影響進行研究.

2 強流電子束阻抗對RKA調制特性影響的理論研究

在RKA中,為了減弱空間電荷效應,一般采用無箔二極管產生的環形電子束作為由電能向高頻能量轉換的媒質.設二極管的加速電壓為V0,則電子到達陽極時的動能,亦即電子從二極管區獲得的能量為

其中e為電子電量,γinj為電子到達陽極時的相對論因子,m0為電子靜止質量,c為光速.環形電子束在導引磁場的約束下由二極管區進入到漂移管.圖1為漂移管中薄環形束示意圖,假定束的厚度為零.在漂移管中,由于直流空間電荷效應,在束流橫截面上產生電位降,使電子束在陽極處的動能的一部分轉化為勢能.根據能量守恒定律,電子束在漂移管中的動能與勢能之和等于電子束在陽極處的動能,即

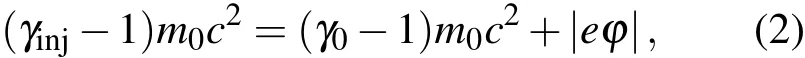
其中γ0=(1?β20)?1/2為電子在漂移管中的相對論因子,β0=v0/c為電子相對速度,v0為電子的速度,(γ0?1)m0c2為漂移管中電子的動能,|eφ|為漂移管中電子的靜電勢能.

由圖1,漂移管半徑為rw,電子束半徑為rb,設環形電子束面電荷密度為σ,則電子束的電流為I0=2πrbσ·v0.由高斯定理可得薄環形電子束的電勢為[9]

其中,ε0為真空中的介電常數.將(3)式代入(2)式并歸一化得

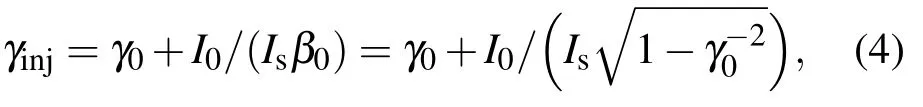
式中,Is=2πε0m0c3/|e|ln(rw/rb)稱為歸一化臨界電流[10],將常數代入后為Is=8.53/ln(rw/rb),單位為kA.由(4)式可知,漂移管中電子束的動能不再等于注入能量,而是由注入能量、漂移管的結構及束流參數共同決定.

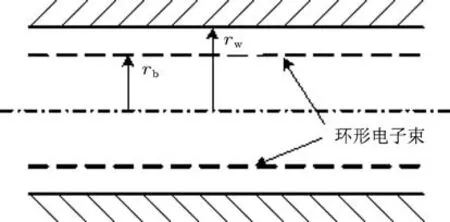
圖1 無限長漂移管中的薄環形電子束

為了得到電子束的勢能、空間電荷限制電流等與電子束流的定量關系,可以用圖解法求解(4)式.將(4)式右邊設為一個函數

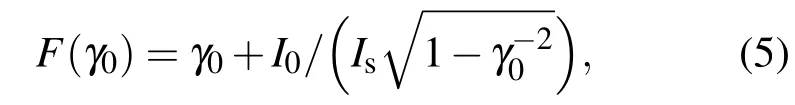
以電子束的動能因子γ0為自變量,以電子束流為參數,畫出y=γinj和y=F(γ0)的曲線,則兩曲線的交點即為(4)式的解.此解給出的是在一定漂移管結構尺寸下,相同注入能量的電子束在不同束流時具有的不同動能因子.因為電子束流的大小是由動能因子和束密度決定的,因此以電子束流為參數求解時,其實隱含了一個條件,即以求出的動能因子和束流再次決定電子束的密度,這樣才能滿足束流不變的前提.圖2為γinj=1.99,Is=78.9 kA時(漂移管半徑及電子束半徑分別取為3.0及2.7 cm),不同束流下(4)式解的情況.

由圖2可見,(4)式的解有三種情況:一是當束流低于空間電荷限制流時,曲線與直線相交,有兩個可能的解,根據束流不變的隱含假定,值較小的解代表低速度高密度的束流,值較大的解代表高速度低密度的束流,在二極管自然發射電子束的情況下,電子束會以高速度低密度的形式存在,而只有人為施加影響的情況下,才會出現低速度高密度的形式,而在RKA中,電子束是爆炸發射的,因此在求解中選擇高速低密的解;當束流等于空間電荷限制流時,曲線與直線相切,此時的解為束流等于空間電荷限制流時電子束的動能因子;當束流大于空間電荷限制流時,解不存在,對應著有虛陰極形成的情況.在RKA中,電子束直流電流一般小于空間電荷限制流,因此只需第一種情況下的解.

圖2 圖解法求解(4)式

由圖解法得到漂移管中強流電子束的動能因子后,就可以對電子束受到調制后的群聚情況進行分析.由RKA的小信號理論可知,在強流電子束受到電壓為V1的調制后,會在漂移管中激勵起快、慢空間電荷波,它們的色散特性為[10]

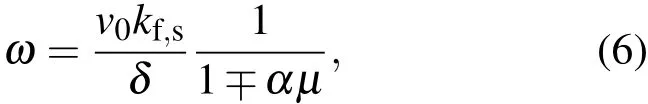
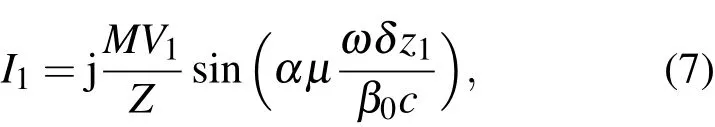
其中M為間隙耦合系數,一般情況下小于1,而

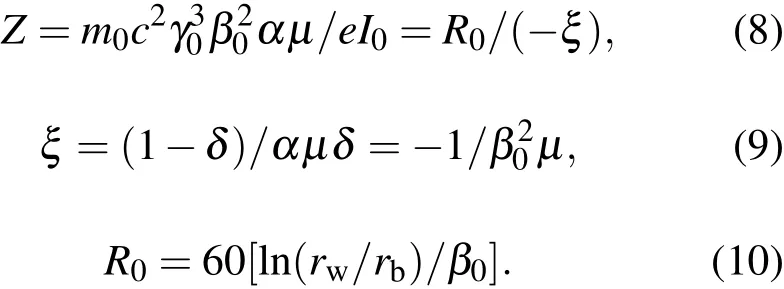
由(7)式可知,基波電流達到最大值的位置與束流狀態及頻率有關,此最大值的位置稱為群聚距離,其表達式為

在調制頻率及漂移管半徑不變的情況下,zmax的值只與束流特性有關.保持二極管電壓不變,只改變二極管的電流,可由(4)式得到電子束的動能隨束流大小變化的曲線,如圖3所示.由(11)式可得到群聚距離隨束流變化的曲線,如圖4所示.由圖3可知,注入電壓不變時,電子束在漂移管中的動能隨束流的增大而減小.由圖4可知,束流經輸入腔調制后,群聚距離隨束流的增大而減小.

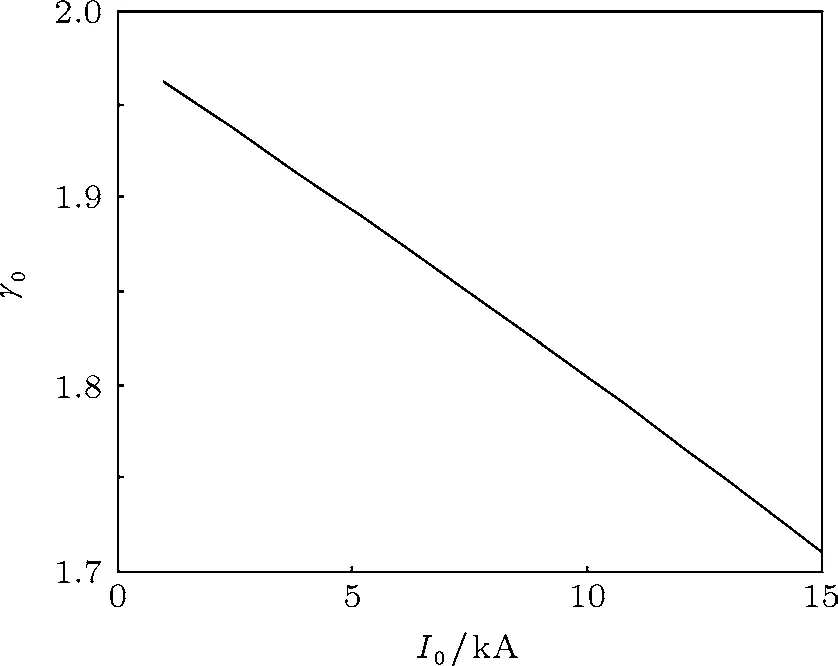
圖3 電子束相對論因子隨束流的變化

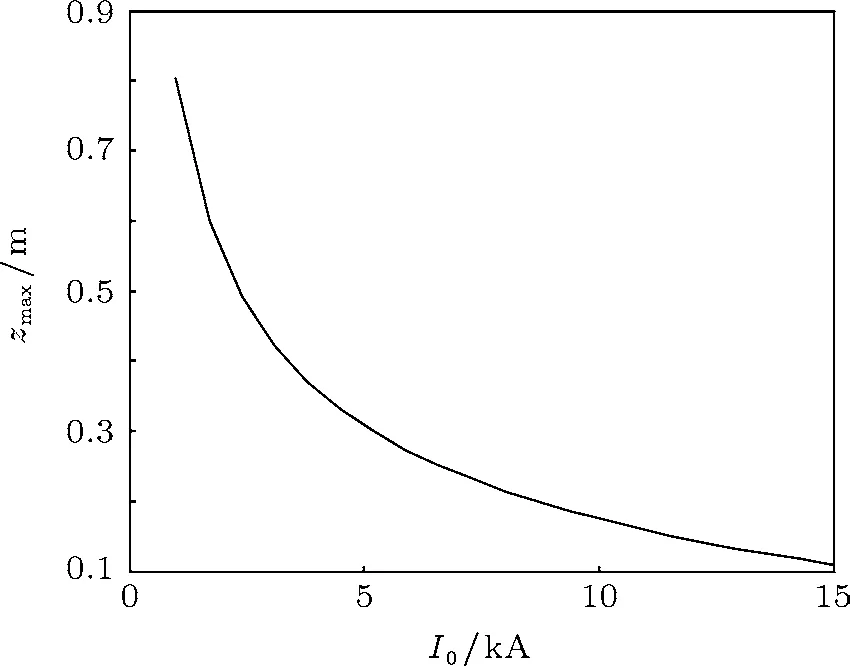
圖4 群聚距離隨束流的變化

保持二極管阻抗不變,改變陰陽極間的電壓,漂移管中電子束的相對論因子與群聚距離也會相應發生變化,其變化規律如圖5和圖6所示.由圖5可以看出,雖然在阻抗不變的情況下二極管電壓增大會導致束流也增大,但是漂移管中電子束的相對論因子還是增加的.由圖6可知,二極管阻抗不變而增大二極管電壓時,群聚距離增大.即在阻抗不變時,二極管電壓對群聚特性的影響優先于束流變化對群聚特性的影響.

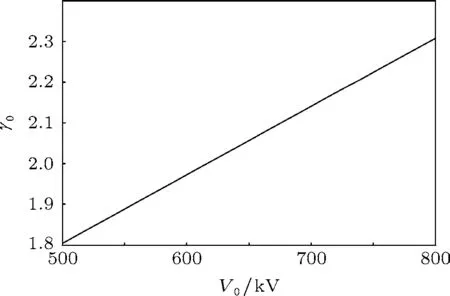
圖5 電子相對論因子隨二極管電壓的變化

圖6 群聚距離隨二極管電壓的變化

3 強流電子束阻抗對RKA調制特性影響的粒子模擬研究

以上的理論研究只能得到諸如電子束動能、群聚距離等信息,而不能得到電子束對輸入腔的加載特性.為了驗證上述理論的正確性,同時得到電子束對輸入腔的加載特性,本文采用粒子模擬(particle-in-cell,PIC)的研究方法.

圖7為PIC程序中帶電子束的RKA輸入腔模型.在輸入腔的注入端口,工作頻率為2.84 GHz,功率為500 kW的微波進入輸入腔,在其中建立起電磁場,并對經過輸入腔間隙的電子束進行調制.其中電子束以束方式發射,即直接指定電子束的加速電壓和電流的大小,而忽略二極管的真實阻抗.因此,使用束發射方式可以精確控制電子束的加速電壓及阻抗.基于這個模型,可以研究電子束基波電流的群聚特性、電子束吸收的微波功率以及輸入腔間隙上建立的電壓與電子束阻抗特性之間的關系.

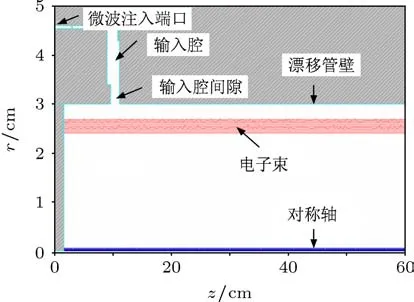
圖7 輸入腔及電子束二維模型示意圖

為了便于說明粒子模擬的結果,把弱流空間電荷波理論中電子負載電導的公式引用如下[14]:

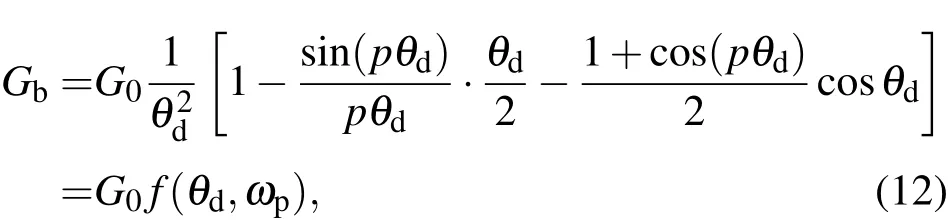
其中,G0=I0/V0為電子束直流電導,p=ωp/ω,為電子束等離子體頻率,θ=dωd/v0為間隙直流渡越角,d為間隙寬度.將渡越角和等離子體頻率對電子負載電導的貢獻看作函數 f(θd,ωp),如(12)式右邊等式所示.(12)式為非相對論條件下有柵間隙電子負載電導公式,若考慮相對論修正,則還需乘上一個相對論修正系數kM=2/γ0(γ0+1).從電子束與場相互作用的觀點來看,電子負載電導和輸入腔間隙電壓有如下關系:

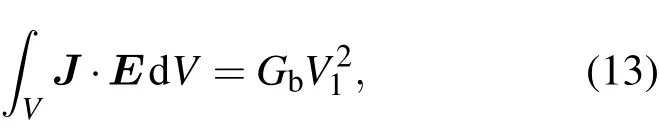
其中,J為電子束電流密度,E為諧振腔內的電場強度,積分區域V為電子束與腔場的作用區域,為電子束吸收的注入微波的有功功率Pin,V1為腔間隙建立的電壓.由等效電路理論,可以將電子束負載品質因數表示為輸入腔特性阻抗和電子束負載電導的關系[15]

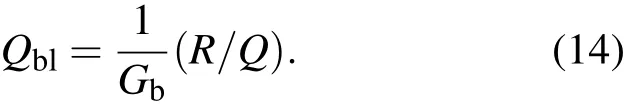
當腔體結構不變時,輸入腔特性阻抗R/Q不變.在輸入功率為P0時(即原始注入功率為500 kW),輸入腔間隙上建立的電壓V1與輸入腔特性及電子束負載品質因數的關系為[16]

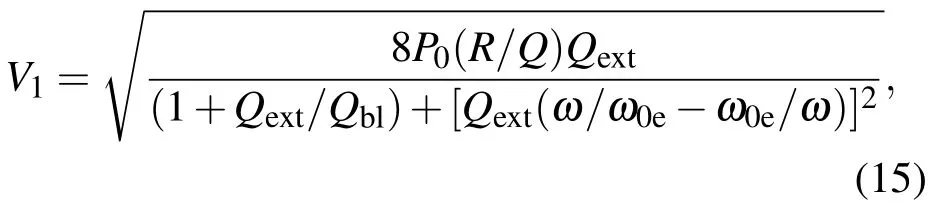
其中,R/Q為輸入腔特性阻抗,Qext為輸入腔外觀品質因數,Qbl為腔體的電子束負載品質因數,ω0e為輸入腔電子束加載諧振頻率.在腔體結構不變時,R/Q,Qext不會變化,而在強流條件下,ω0e也基本不隨束流參數變化.

3.1 電子束阻抗變化情況

固定電子束加速電壓為500 kV,電子束流從3 kA改變到6 kA,將不同電流下基波電流隨距離的變化曲線示于圖8中,每條曲線最大值對應的橫坐標減去輸入腔位置的橫坐標為群聚距離.由圖8可見,隨著電子束阻抗的減小(即電子束電導增大),群聚電流的幅值變化不大(但是基波電流幅值與直流電子束幅值之比減小,即調制深度減小),而群聚距離的減小較為明顯.

圖8 基波電流群聚特性隨電子束流的變化

表1 電子束加載特性隨電子束束流的變化

同時,將這種情況下電子束吸收的注入微波的功率、輸入腔間隙建立的電壓列在表1中.由表1可見,在束流增大的過程中,電子束吸收的功率Pin增大,而在輸入腔間隙建立的電壓V1卻減小,則由(13)式可知,電子負載電導增大.(12)式表明,電子束直流電導的增大會直接導致電子負載電導增大.由這兩方面,在電子束直流電導增大的過程中,渡越角和等離子體頻率對電子負載電導的貢獻f(θd,ωp)弱于直流電導G0對電子負載電導Gb的貢獻.而由(14)式知,Gb增大將導致電子束對腔體的負載品質因數Qbl變小,為了達到匹配注入的狀態[17],輸入腔的外觀品質因數要相應地降低,故注入耦合孔尺寸要變大.

從物理上可以這樣解釋:在束流增大而電壓不變時,電子束在漂移管中的相對論因子減小,即電子的速度減小,因此渡越輸入腔間隙的時間增長,則輸入腔內的場對電子束所做的功增大,因此電子束吸收的功率增大,也即等效于電子束的負載品質因數Qbl變小.由(15)式可知,Qbl變小時,V1減小.

圖9給出了電子束流為3和6 kA時的電子束群聚的能量相空間圖.從圖9中可以看到,電子束流越大,調制效果越不明顯.

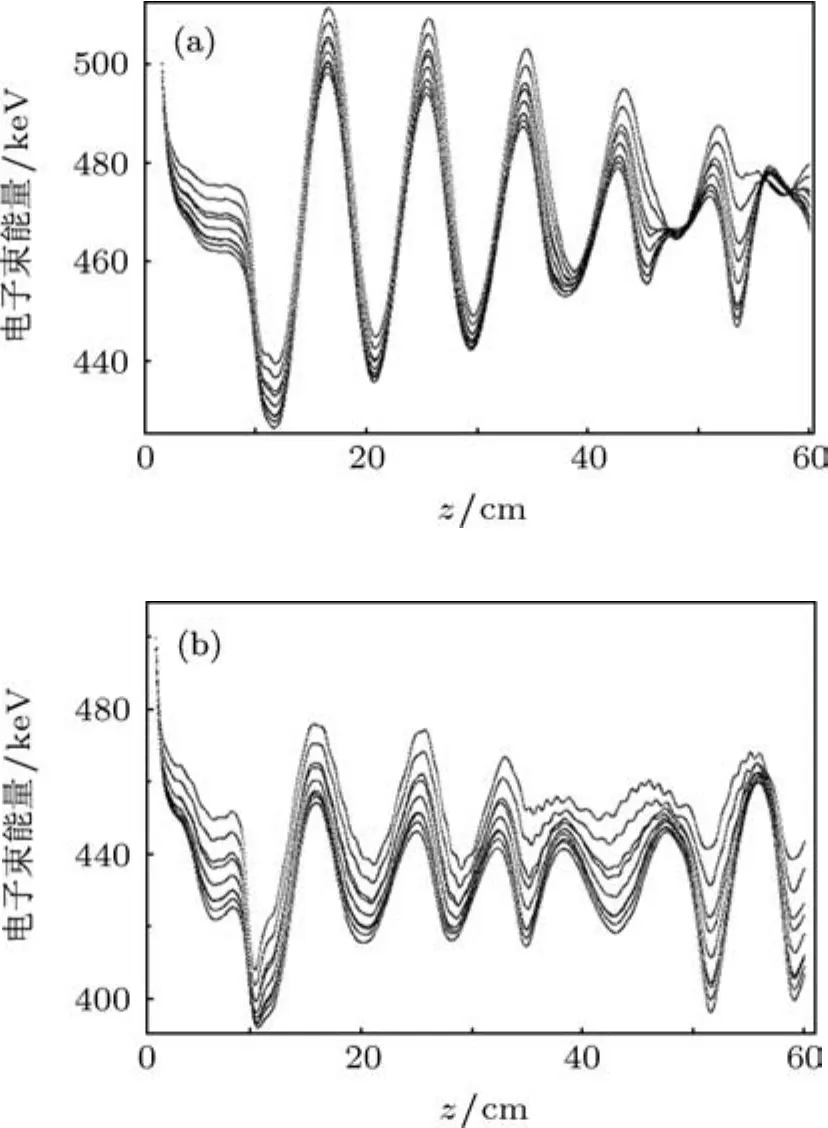
圖9 兩種束流情況下的電子束群聚相空間圖 (a)束流為3 kA;(b)束流為6 kA

由上述情況可知,電子束阻抗越低,群聚距離越短,在輸入腔間隙建立的電壓越小,為了達到同樣的調制深度,對注入微波功率水平的要求越高.

3.2 二極管阻抗不變的情況

保持二極管阻抗不變,改變二極管電壓,基波電流隨距離的變化曲線也會改變,如圖10所示.從圖10中可知,隨著二極管電壓的增大,基波電流群聚距離增加,同時基波電流的幅值增大.

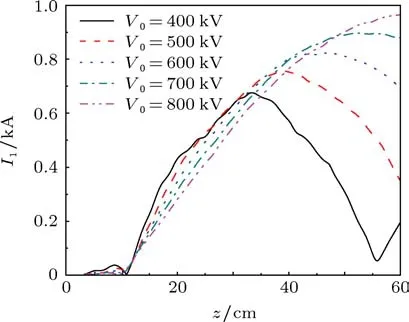
圖10 基波電流隨二極管電壓的變化情況(二極管阻抗固定為100?)

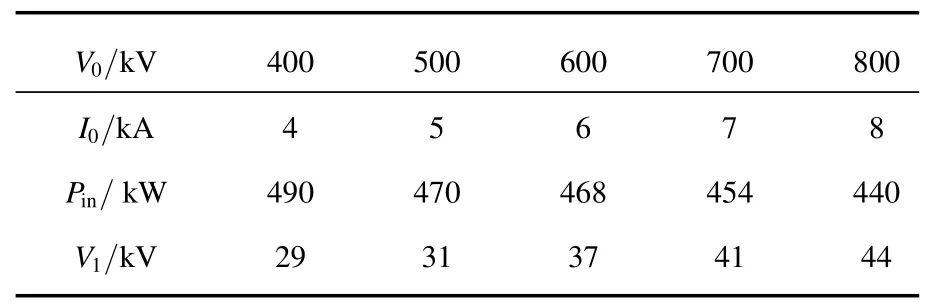
表2 阻抗不變時電子束加載特性隨二極管電壓的變化

表2給出了阻抗不變時電子束加載特性.由表2可知,在二極管阻抗不變時,即電子束直流電導不變時,二極管電壓V0越高,電子束吸收的注入功率Pin越小,但是在輸入腔間隙建立的電壓V1卻越大.由(13)式可知,在這個過程中,電子束負載電導減小.由于這種情況下電子束直流電導沒有變化,那么由(12)式可知,電子負載電導的變化完全來自渡越角和等離子體頻率的貢獻 f(θd,ωp),而且可知f(θd,ωp)是隨著二極管電壓的增大而減小的.

從物理機理上解釋,在二極管阻抗不變而電壓增大的過程中,由圖5可知電子束在漂移管中的相對論因子增大,即電子的速度增大,因此渡越輸入腔間隙的時間減小,則電子束從輸入腔中吸收的功率減小,即等效為電子束對腔體的負載品質因數增大.為了達到匹配注入條件,輸入腔的外觀品質因數也相應地增大,從而耦合孔尺寸要減小.同樣,由(15)式可知電子束負載品質因數增大會導致輸入腔間隙電壓增大.

由上述情況可知,在阻抗不變時,二極管電壓越高,群聚距離越長,在輸入腔間隙建立的電壓越大.為了達到同樣的調制深度,對注入微波功率水平的要求也越低.

4 結論

通過數值計算和PIC模擬,對強流電子束阻抗對RKA注入和群聚特性的影響進行了分析.強流電子束阻抗對RKA的群聚特性影響的研究表明,低阻抗電子束有利于減小群聚距離,縮短RKA器件的整體長度,不利于注入微波對電子束的調制.高阻抗電子束情況正好相反.在電子束阻抗不變時,增加電子束加速電壓類似于增大電子束阻抗的情況.強流電子束阻抗對RKA注入特性的研究表明:強流電子束阻抗降低時,電子電導變大,對腔體的負載品質因數變小,要求輸入腔有較低的外觀品質因數,同時要求較高的注入微波功率水平.電子束阻抗增大時結果正好相反.在設計RKA的過程中,可以根據實際情況,例如根據所設計器件的長度、種子源功率水平,以及輸入腔耦合方式等對二極管阻抗進行選擇,或者進行相反的選擇.同軸多注速調管放大器[18]的注入功率只需幾十千瓦,原因之一是同軸結構中束流阻抗較高,因此對輸入腔的加載減輕,所需注入功率也減小.

[1]Ding Y G 2010 Design,Manufacture and Application of High Power Klystron(Beijing:National Defense Industry Press)pp8–17(in Chinese)[丁耀根2010大功率速調管的設計制造和應用(北京:國防工業出版社)第8—17頁]

[2]Huang H,Fan Z K,Tan J,Ma Q S,Gan Y Q,Chang A B 2004 Acta Phys.Sin.53 1129(in Chinese)[黃華,范植開,譚杰,馬喬生,甘延青,常安碧2004物理學報53 1129]

[3]Huang H,Meng F B,Fan Z K,Li Z H 2006 Acta Phys.Sin.55 5344(in Chinese)[黃華,孟凡寶,范植開,李正紅2006物理學報55 5344]

[4]Bai X C,Yang J H,Zhang J D 2012 Phys.Plasma 19 083106

[5]Liu J,Shu T,Li Z Q 2010 Acta Phys.Sin.59 2622(in Chinese)[劉靜,舒挺,李志強2010物理學報59 2622]

[6]Liu J,Shu T,Li Z Q 2010 High Power Laser and Particle Beams 22 1(in Chinese)[劉靜,舒挺,李志強2010強激光與粒子束22 1]

[7]Benford J,Swegle JA,Schamiloglu E(translated by Jiang WH,Zhang C)2009 High Power Microwaves(2nd Ed.)(Beijing:National Defense Industry Press)p315(in Chinese)[Benford J,Swegle JA,Schamiloglu E著(江偉華,張馳譯)2009高功率微波(第二版)(北京:國防工業出版社)第315頁]

[8]Wu Y,Xu Z,Xu Y,Jin X,Chang A B,Li Z H,Huang H,Liu Z,Luo X,Ma Q S,Tang C X 2011 Acta Phys.Sin.60 044102(in Chinese)[吳洋,許州,徐勇,金曉,常安碧,李正紅,黃華,劉忠,羅雄,馬喬生,唐傳祥2011物理學報60 044102]

[9]Miller R B(translated by Liu X S,Zhang L Z,Wu Y B,Lu J P,Zhou P Z)1990 Introduction to the Physics of Intense Charged Particle Beam(Beijing:Atom Energy Press)p92(in Chinese)[米勒R B著(劉錫山,張蘭芝,吳衍斌,魯敬平,周丕璋譯)1990強流帶電粒子束物理學導論(北京:原子能出版社)第92頁]

[10]Friedman M,Krall J,Lau Y Y,Serlin V 1988 J.Appl.Phys.64 7

[11]Briggs R J 1976 Phys.Fluids 19 1257

[12]Lau Y Y 1987 J.Appl.Phys.62 351

[13]Qi Z M,Zhang J,Zhong H H,Zhang Z H,Bai X C,Zhang D,Bai Z 2012 IEEE Trans.Plasma Sci.40 41

[14]Xie J L,Zhao Y X 1966 Bunching Theory of Klystron(Beijing:Science Press)p77(in Chinese)[謝家麟,趙永翔1966速調管群聚理論(北京:科學出版社)第77頁]

[15]Zhang Z T 1982 Measurement of High Frequency System in Microwave Tubes(1st Ed.)(Beijing:National Defense Industry Press)p18(in Chinese)[張兆鏜1982微波管高頻系統的測量(第一版)(北京:國防工業出版社)第18頁]

[16]Ding Y G 2008 Theory and Computer Simulation of High Power Klystron(Beijing:National Defense Industry Press)p75(in Chinese)[丁耀根2008大功率速調管的理論與計算模擬(北京:國防工業出版社)第75頁]

[17]Carlsten B E,Faehl R J,Fazio M V,Haynes W B,Ryne R D,Stringfi eld R M 1994 IEEE Trans.Plasma Sci.22 730

[18]Liu Z B,Huang H,Jin X,Chen H B 2012 Acta Phys.Sin.60 128402(in Chinese)[劉振幫,黃華,金曉,陳懷壁2012物理學報60 128402]