Laasraoui-Jonas位錯密度模型結合元胞自動機模擬AZ31鎂合金動態再結晶

劉 筱 ，朱必武 ，李落星

(1.湖南大學 汽車車身先進設計制造國家重點實驗室，長沙 410082；2.湖南大學 機械與運載工程學院，長沙 410082)

鎂合金因密度小、比強度高和比剛度高等優點，在汽車、航空和電子等領域得到廣泛的應用[1-3]。但是，制約變形鎂合金發展的主要原因在于其較差的室溫塑性變形能力，如何在較大程度上改善鎂合金的塑性已成為人們關注的焦點。改善的方法主要包括合金化和晶粒細化等[4]，晶粒細化的方法主要有動態再結晶、快速凝固、噴射沉積、強應變塑性變形等。鎂合金是低層錯能金屬，與鋁等高層錯能金屬相比，鎂合金在熱變形過程中發生動態再結晶[5]。所以，鎂合金動態再結晶組織的模擬和預測已經成為鎂合金熱加工數值模擬技術的研究重點。

再結晶的驅動力來至于變形過程中的位錯密度的消散[6]。從而，選擇適合 AZ31鎂合金的位錯密度模型對再結晶過程的模擬起到很重要的作用。目前，模擬材料內部位錯密度變化的模型包括修正的L-J位錯密度模型、KM位錯密度模型、兩個參數位錯密度模型和多參數位錯密度模型等。KM 位錯密度模型的主要特征是材料的變形機制由總的位錯密度決定；兩個參數模型具有KM模型的特征，但是將總的位錯密度分成了遷移的位錯密度和積累位錯密度；多參數位錯密度模型則考慮了亞晶粒尺寸的影響[7]。修正的 L-J位錯密度模型不僅僅具有KM位錯密度模型的特征，同時考慮了晶界遷移對位錯演變的影響。

本文作者通過熱模擬實驗得到AZ31鎂合金流變應力曲線，根據流變應力曲線的圖形轉換得到硬化率曲線，/θσ??—σ曲線，曲線，最終得到不同應變速率下lnr—1/T的曲線，表明回復參數在不同應變速率下的自然對數與溫度的倒數具有線性相關的關系，并且斜率基本相同，證實了修正的L-J位錯密度模型適用于AZ31鎂合金動態再結晶過程中位錯密度的計算，采用修正的L-J位錯密度模型結合CA方法模擬的AZ31鎂合金的動態再結晶結果與實驗結果相似。

1 實驗

實驗為了保證所有的鎂合金樣品晶體取向保持一致(即是所有的樣品具有相同初始條件)，采用 AZ31擠壓態鎂合金，成分(質量分數，%)為Al 2.8～3.2，Mn 0.2～1.0，Zn 0.8～1.2, Si不大于 0.05，Cu 不大于 0.05，Ni不大于0.005，Fe不大于0.005，雜質不大于0.3，余量為 Mg。沿擠壓棒的長度方向在中心截取直徑為10 mm，高為12 mm的圓柱體試樣，在Gleeble-3500熱模擬試驗機進行等溫壓縮變形實驗，預設溫度為300～500 ℃、應變速率為 0.03～3 s-1，真應變為 1，并獲取流變應力曲線。采用LeitZ-MM-6臥式金相顯微鏡觀察合金壓縮后的顯微組織。

2 動態再結晶模型

2.1 位錯密度模型

動態再結晶過程是一個加工硬化、動態回復和再結晶的過程。這些過程導致位錯密度的變化,既是加工硬化導致位錯的堆積，動態回復和再結晶導致位錯的消散，最終體現流變應力的變化[6,8-10]。

Laasraoui-Jonas(L-J)位錯密度模型(見式(1))表達了位錯密度在晶粒內的演變。流變應力與位錯密度的關系見式(2)。

式中：ρ表示位錯密度；ε表示應變增量；h表示硬化參數；r表示回復參數；α表示泰勒因子，一般為0.5；μ表示剪切模量；σ表示的流變應力。

根據式(1)和(2)可知，位錯密度的變化體現了材料的微觀變化，流變應力體現的是材料的宏觀變化，同時流變應力是依賴位錯密度的變化。

再結晶過程也是一個形核和長大過程，晶粒長大過程中的晶界遷移會造成位錯的消散，GOURDET和MONTHEILLET[11]采用修正的L-J位錯密度模型(見式(3))其考慮了溫度和應變速率的影響，其中回復參數表示如式(4)。

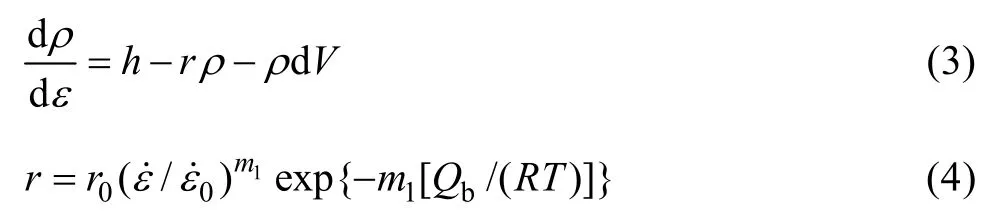
式中：dV表示晶界遷移掃過的體積；ε˙表示應變速率；0ε˙表示應變速率校準常數；m1是常數；Qb是自擴散激活能；R是摩爾氣體常數；T是絕對溫度。

2.2 形核和長大模型

金屬在一定再結晶溫度以上變形，短時間內發生回復，長時間加熱，發生再結晶。再結晶新晶粒的形成是形核和長大的兩個基本過程[12]。

2.2.1 形核模型

XIAO等[13]根據實驗和理論分析，提出動態再結晶形核速率不僅僅與溫度和應變速率有關，同時也與應變量有關(見式(5))。

式中：n˙表示的形核率；C、m、p為常數；Z是Zenner-Hollomon參數；cε是臨界應變。

2.2.2 長大模型

當位錯密度和應變達到臨界值時，開始發生再結晶，即有新晶粒的生長。DING和 GUO[7]、CHEN等[8]以及李落星等[14]采用式(6)表達新晶粒生長速度(vi)。

式中：M表示邊界遷移(見式(7))；Fi表示第i個新晶粒驅動力(見式(8))；ri表示晶粒半徑。

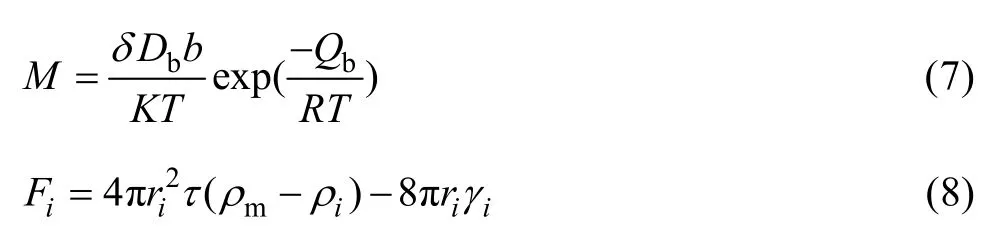
式中：δ為晶粒邊界厚度；b為柏氏矢量；Db表示邊界自擴散有效系數；K為波爾赫茲常數；ρm表示母相的位錯密度；ρi表示第i個新晶粒的位錯密度；γi表示晶界能；τ是位錯線能量。

3 結果和分析

3.1 流變應力曲線

圖1所示為AZ31鎂合金應變速率為0.03、0.3和3 s-1下溫度為300、350、400、450和500 ℃、真應變為1時的流變應力曲線。流變應力曲線表現出很明顯的單峰值，是典型的連續動態再結晶，那么在相對高的應變速率和相對低的溫度下晶粒尺寸隨著應變的增加而減小[15-16]。圖1(c)顯示應變速率為3 s-1、溫度為300 ℃和 350 ℃時的流變應力曲線從應變量為 0.007開始產生了反C曲線，說明發生了孿生，所以在這種條件下不能采用修正的L-J位錯密度模型進行微觀組織模擬。

3.2 硬化率曲線

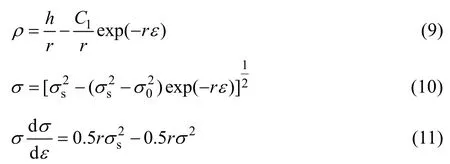
式(9)、(10)、(11)中：C1表示常數；σ0為屈服應力。

圖4所示為根據式(11)求解的斜率(r)。式(4)表明，如果式(3)適用于材料動態再結晶過程中位錯密度的演變的計算那么不同應變速率下的回復參數r的自然對數與溫度的倒數 1/T成線性相關關系并且斜率相似，從而圖5表明修正的L-J位錯密度模型(式(3))適用于AZ31鎂合金動態再結晶過程中的位錯密度演變的計算。

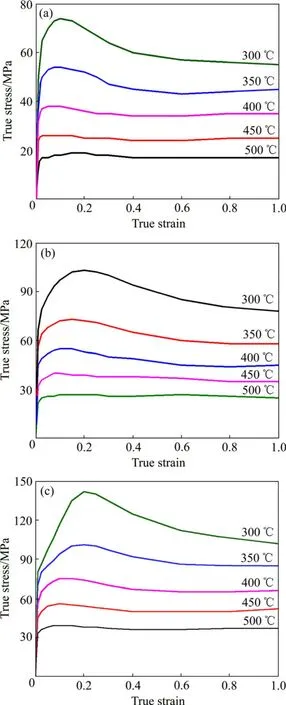
圖1 相同應變速率下不同溫度的流變應力曲線Fig.1 Flow stress curves under different temperatures and strain rates: (a)ε˙=0.03 s-1; (b)ε˙=0.3 s-1; (c)ε˙=3 s-1

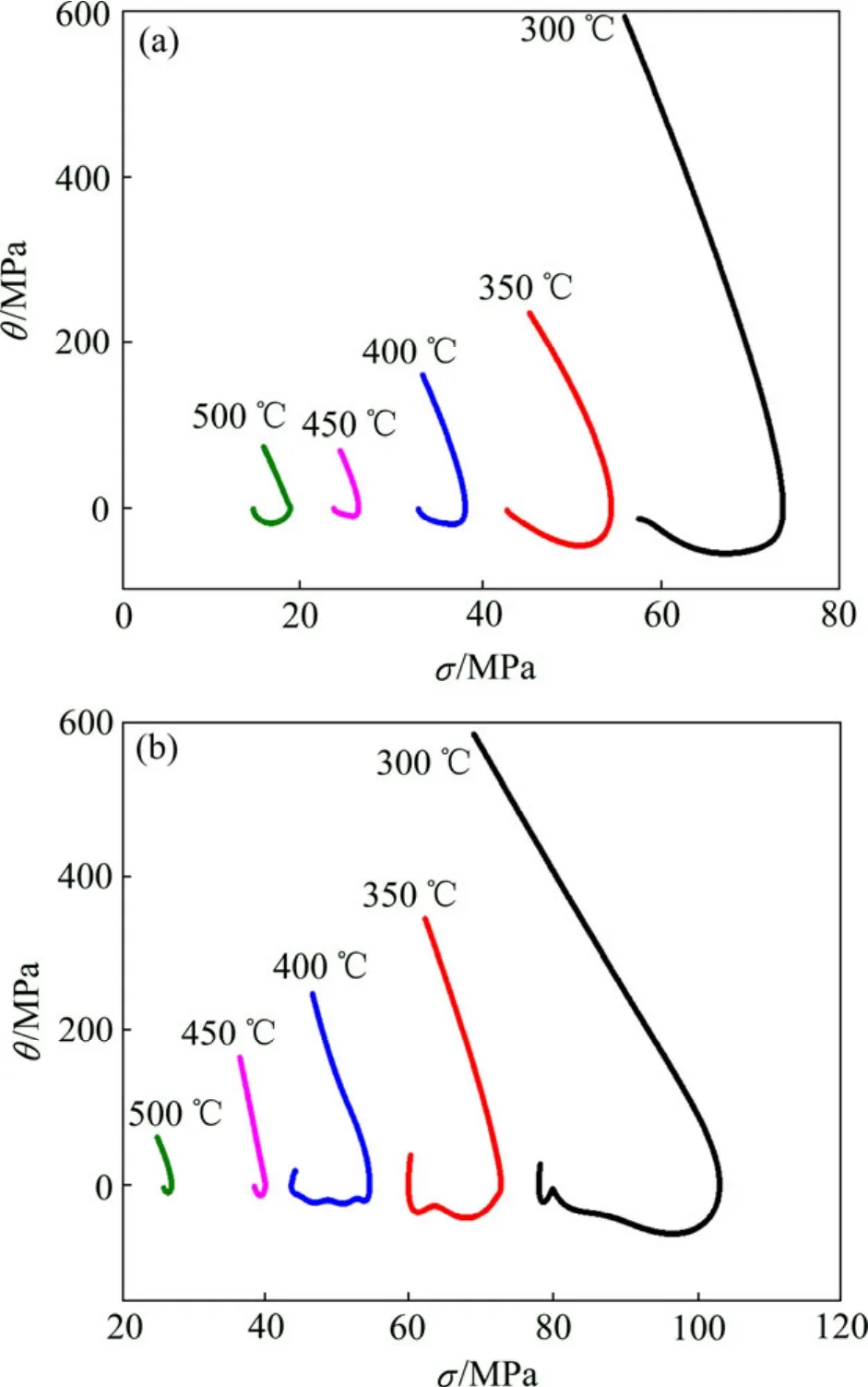
圖2 相同應變速率下不同溫度的硬化率曲線Fig.2 Work hardening rate curves at different temperatures:(a)ε˙=0.03 s-1; (b)ε=3 s-1

圖3 應變速率為 0.3 s-1時不同溫度下的流變應力基于θ=-?θ/?σ 的曲線Fig.3 Flow stress dependence of θ=-?θ/?σ at strain rate of 0.3 s-1 and different temperatures

圖4 2σθ與 σ2關系曲線Fig.4 Relationship curves between 2σθ and σ2: (a)ε= 0.03 s-1;(b)ε=0.3 s-1

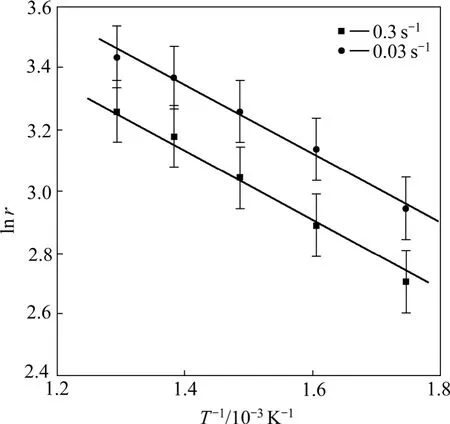
圖5 ln r —1/T的關系曲線Fig.5 Relationship curves between ln r and 1/T

3.3 模擬結果和分析

采用修正的L-J 位錯密度模型結合CA方法模擬AZ31鎂合金的動態再結晶過程。CA(Cellular Automata)是一種用來描述系統在離散空間—時間上演化規律的數學算法[18]。本文作者將模擬區域劃分為150×150網格，每個網格表示2 μm，模擬0.3 mm×0.3 mm的實際樣品區域。模擬所用的材料常數如下表1。

圖6所示為應變速率為0.03 s-1、真應變為1時不同溫度下模擬的微觀組織。觀察模擬的微觀組織，晶粒基本為等軸晶結構，并且隨著溫度的增加，晶粒尺寸也隨之增加。這是由于隨著溫度的升高，晶界遷移速度增加，同時形核率下降，從而新生晶粒有足夠的空間生長，導致晶粒粗化。圖7所示為實驗的微觀組織。由圖7可看出，隨著溫度的增加，晶粒粗化。比較圖6和7可知，模擬的結果與實際的微觀組織相近，模擬的晶粒尺寸的變化規律與實際相符，證明了修正的 L-J位錯密度模型結合 CA可以準確的模擬AZ31鎂合金的動態再結晶。

表1 AZ31合金的材料參數Table 1 Materials parameters of AZ31 magnesium alloy

表2所列為模擬的晶粒尺寸和實際的晶粒尺寸的比較。通過表1表明模擬的晶粒尺寸與實際的再結晶粒尺寸誤差在8%以內。

圖8所示為不同溫度下應變速率分別為 0.03和0.3 s-1模擬的流變應力曲線與實驗的流變應力曲線。結果表明，模擬曲線與實驗曲線存在誤差，這是由于在模擬時將初始狀態理想化，例如均勻的位錯和能量分布以及隨機的晶粒取向，忽略材料本身某些位置的位錯堆積和能量起伏等情況。但是總體來說，模擬的結果與實驗結果一致，進一步證明了修正的 L-J位錯密度模型可以用于AZ31鎂合金位錯密度演變的計算。

圖6 應變速率為0.03 s-1和真應變為1時不同溫度下的模擬微觀組織Fig.6 Simulated microstructures under different temperatures at strain rate of 0.03 s-1 and true strain of 1: (a)300 ℃; (b)400 ℃;(c)500 ℃

圖7 應變速率為0.03 s-1和真應變為1時不同溫度下的金相組織Fig.7 Optical microstructures under different temperatures at strain rate of 0.03 s-1 and true strain of 1: (a)300 ℃; (b)400 ℃; (c)500 ℃

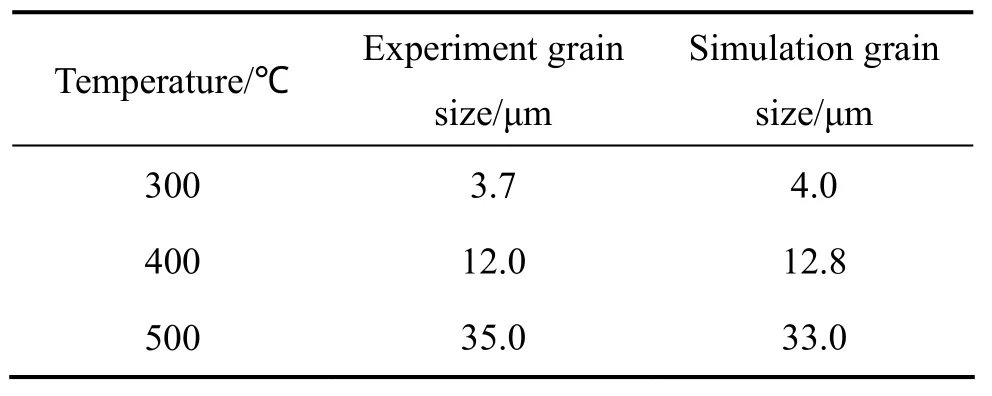
表2 應變速率為0.03 s-1和真應變為1時不同溫度模擬的晶粒尺寸和實驗數據的比較Table 2 Comparison of final grain size for simulation with experimental data at strain rate of 0.03 s-1 and true strain of 1

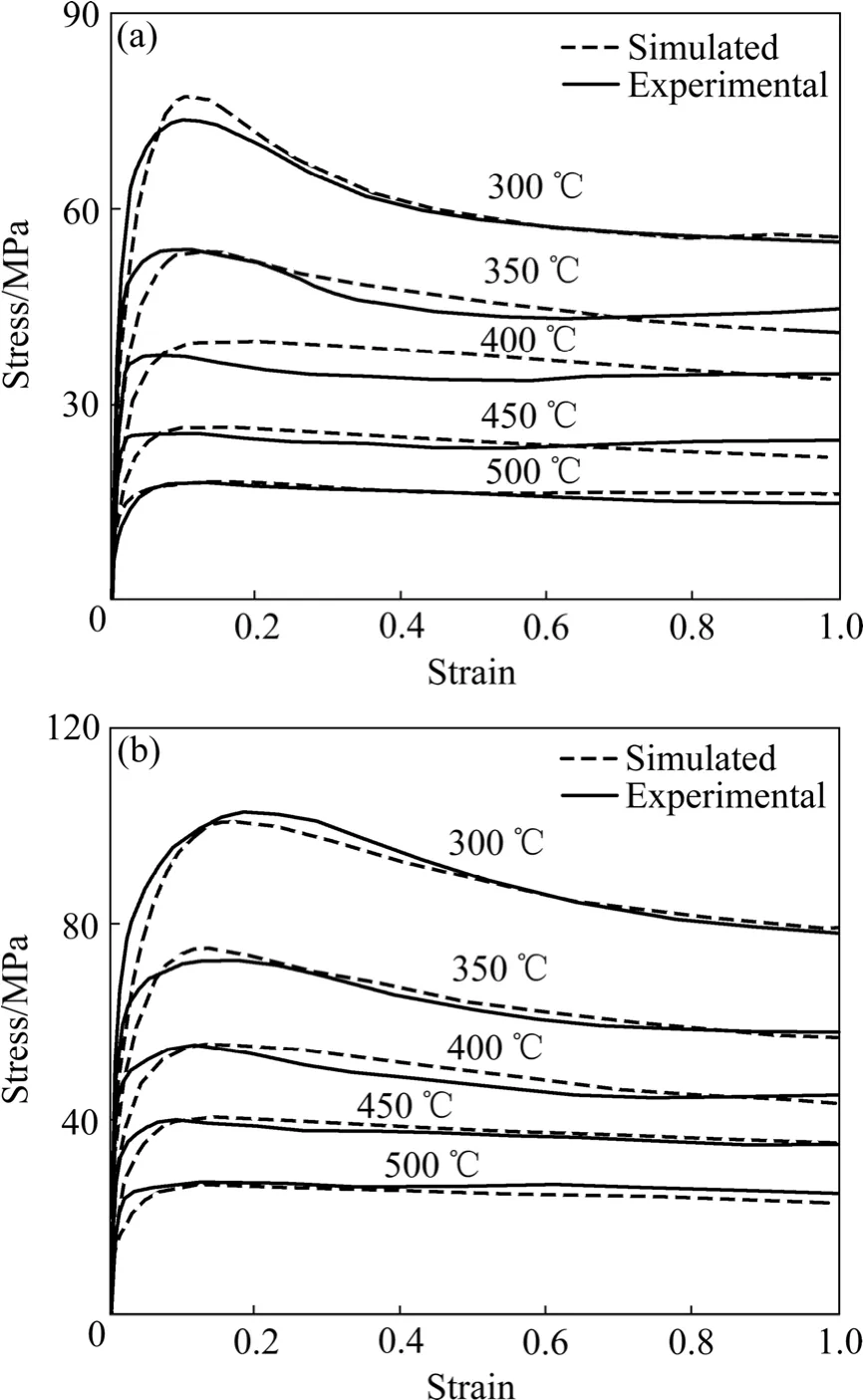
圖8 不同溫度下模擬的流變應力曲線和實驗的流變應力曲線Fig.8 Simulated and experimental curves at different temperatures: (a)0.03 s-1; (b)0.3 s-1

4 結論

1)通過AZ31鎂合金流變應力曲線分析和圖形變換求解不同應變速率下的回復參數r，其自然對數lnr與溫度倒數1/T呈線性相關關系，并且不同應變速率下，lnr—1/T斜率相似，表明可以采用修正的L-J位錯密度模型進行動態再結晶過程中的位錯密度演變計算。

2)通過采用修正的L-J位錯密度模型結合CA可以準確地模擬AZ31鎂合金的動態再結晶演變過程。

[1]AGHION E, BRONFIN B.Magnesium alloys development towards the 21st century[J].Materials Science Forum, 2000,350/351: 19-30.

[2]王文先, 張金山, 許并社.鎂合金材料的應用及其加工成型技術[J].太原理工大學學報, 2001, 32(6): 599-610.WANG Wen-xian, ZHANG Jin-shan, XU Bing-she.Application and modeling technology for magnesium alloy materials[J].Journal of Taiyuan University of Technology, 2001, 32(6):588-610.

[3]FRIEDRICH H, SCHUMANN S.Research for a “new age of magnesium” in the automotive industry[J].Mater Process Tech,2002, 1l7(3): 276-281.

[4]陳振華, 夏偉軍, 程永奇, 傅定發.鎂合金織構和各向異性[J].中國有色金屬學報, 2005, 15(1): 1-11.CHEN Zhen-hua, XIA Wei-jun, CHEN Yong-qi, FU Ding-fa.Texture and anisotropy in magnesium alloys[J].The Chinese Journal of Nonferrous Metals, 2005, 15(1): 1-11.

[5]陳振華.變形鎂合金[M].北京: 化學工業出版社, 2005.CHEN Zhen-hua.Wrought magnesium alloy[M].Beijing:Chemical Industry Press, 2005.

[6]HUMPHREYS F J, HATHERLY M.Recrystallization and related annealing phenomena[M].Oxford: Pergamon, 1995.

[7]DING R, GUO Z X.Coupled quantitative simulation of microstructure evolution and plastic flow during dynamic recrystallization[J].Acta Materialia, 2001, 49: 3163-3175.

[8]CHEN Fei, CUI Zhen-shan, LIU Juan, ZHANG Xiao-xun,CHEN Wen.Modeling and simulation on dynamic recrystallization of 30Cr2Ni4MoV rotor steel using the cellular automaton method[J].Modeling and Simulation in Materials Science and Engineering, 2009, 17: 1-19.

[9]JONAS J J, QUELENNEC X, JIANG L, MATIN é.The Avrami kinetics of dynamic recrystallization[J].Acta Materialia, 2009,57: 2748-2756.

[10]FURRER D U, SEMIATIN S L.A Fundamental of Modeling for Metal Processing[M].New York: ASM Handbook, 2009, 22A.

[11]GOURDET S, MONTHEILLET F.A model of continuous dynamic recrystallization[J].Acta Materialia, 2003, 51:2685-2699.

[12]潘金生, 全健民, 田民波.材料科學基礎[M].北京: 清華大學出版社, 2007.PAN Jin-sheng, QUAN Jian-min, TIAN Min-bo.Foundation of materials science[M].Beijing: Tsinghua University Press, 2007.

[13]XIAO Hong, XIE Hong-biao, YAN Yan-hong, JUN Y.Simulation of dynamic recrystallization using automaton method[J].J Iron & Steel Res Int, 2004, 11(2): 42-45.

[14]李落星, 何鳳儀, 劉 筱, 周 佳.AM80-0.2Sr-1.5Ca鎂合金高溫壓縮過程的動態再結晶模擬[J].湖南大學學報:自然科學版, 2011, 12: 46-51.LI Luo-xing, HE Feng-yi, LIU Xiao, ZHOU Jia.Simulation of the dynamic recrystallization of AM80-0.2Sr-1.5C magnesium alloy during hot compression deformation[J].Journal of Hunan University: Natural Science, 2011, 12: 46-51.

[15]SAKAI T, JONAS J J.Dynamic recrystallization: Mechanical and microstructural considerations[J].Acta Metall, 1984, 31(2):189-209.

[16]WEISS I, ALVARADO P J, FITZSIMONS G, DEARDO A J.Grain refinement and coarsening during dynamic recrystallization in plain carbon steel[J].Scripta Metallurgica,1983, 17: 693-697.

[17]POLIAK E I, JONAS J J.A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J].Acta Metallurgica, 1996, 44(1): 127-136.

[18]何 燕, 張立文, 牛 靜, 裴繼斌.元胞自動機再結晶過程模擬[J].材料熱處理學報, 2005, 26(4): 120-125.HE Yan, ZHANG Li-wen, NIU Jing, PEI Ji-bin.Simulation of dynamic recrystallization process using cellular automata[J].Transactions of Materials and Heating Treatment, 2005, 26(4):120-125.